International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1572

ISSN 2229-5518

Voltage Stability Analysis

A.S.Ravi, Ashutosh Dwivedi, Bhuvan Sharma

Abstract— Voltage Stability is a serious concern of today power system for its secure and reliable operation. Power system stability is de- pendent mainly on the degree of maintaining the synchronism of the whole system. Out of the all blackouts round the globe the primary reasons for the blackouts are observed to be voltage collapse. There is a need to perform studies to ensure that the reliability of the power system is maintained at all system condition and its different operating horizons. This paper analyzes the voltage stability of a system by finding a continuum power flow solutions with base load and obtaining steady state voltage stability limit the critical point. The in-between result of the process is used to determine voltage stability index and further to identify portion of the system prone to such voltage collapse

Index Terms—Critical Line, Critical Power Flow Path, Line voltage Stability Index, Path Voltage Stability Index,

——————————  ——————————

1 INTRODUCTION

HILE planning and operating today’s power systems, the voltage stability is of major and growing concern. The Power transmission utility requirements have
changed considerably after the deregulation of the power in-
dustry. These changes had brought a considerable unaccepta-
ble poor quality power, which is apparent by continuous in-
crease in sophisticated generation, transmission, distribution and service industries. The modern society where the prime energy source is electricity, the user does not tolerate power outages and other disturbances that impact their conveniences or life style. Social, environmental, right of way costs are ag- gregated by potential problems that hinder the construction of new transmission lines. Introduction of the deregulated energy market has further stressed the transmission grid because of maximized financial returns with minimum investment and deliver energy at a reasonable cost to the ultimate customer. One of the major problems associated with the today stressed system is voltage instability or voltage collapse. Voltage col- lapse is a process, which leads to a reduction of voltage in a significant portion of a power system. The tripping of trans- mission or generating equipment often triggers voltage col- lapse. [1]
Voltage stability is the ability of a power system to main- tain voltage irrespective of the increase in load admittance and load power resulting in control of power and voltage. The pro- cess by which voltage instability leads to the loss of voltage in a significant part of a power system is called voltage collapse. The ability of a power system to operate not only in stable conditions, but also to remain stable following any reasonable contingency or adverse system change is termed a voltage se- curity.
A system enters into the unstable state when a disturbance
(load increase, line outage or other system changes) causes the
voltage drop quickly or to drift downward and, and automatic system controls fail to improve the voltage level. The voltage decay can take a few seconds to several minutes.
Voltage stability or voltage collapse has become a major concern in modern power systems. In deregulated market
conditions, a power system is set to operate at its maximum operating limits to better utilize existing facilities. This kind of system cannot withstand for any network outage. So, it is im- portant to study the system behavior in the case of prolonged overload or any other system disturbances. [1]

2 TYPES OF VOLTAGE STABILITY

2.1 Classification of Voltage Stability

Voltage stability or voltage collapse deals with the ability of a power system to maintain acceptable voltage levels at all buses in the system in any condition whether it is normal or during disturbance. A heavily loaded system enters a state of voltage instability due to a sudden large disturbance or a change in system condition. It causes a progressive and uncontrollable decline in voltage. The main factor causing voltage instability in any power system is the inability of the system to meet its sudden growing demand for reactive power.
The two different approaches available as a tool to ana- lyse the voltage collapse problem in a system are:
(a) The static approach and
(b) The dynamic approach.

(a) Static methods involve the static model of power system

components. These methods are important when the power system is in operation and planning stages, in-order to prepare an ade- quate fool proof plan for meeting the power requirements during different types of contingencies arising during its operation.

(b) The dynamic methods use time domain simulations to re- veal the voltage collapse mechanism such as why and how the volt- age collapse occurs. Dynamic methods analyze the effect of dynam- ic loads, on load tap changes (OLTC), generator over excitation limiters (OXL) on voltage collapse. [1]

In most of the cases, the system dynamics affecting voltage
stability are quite slow. The static approach effectively analyz- es most of the problems. It can examine the viability of a spe- cific operating point of the power system. In addition, static analysis method provides information such as sensitivity or degree of stability and involves the computation of only alge- braic equations. It is much more efficient and faster than dy- namic approaches. The static analysis approach is more attrac- tive than the dynamic method and well suited to voltage sta- bility analysis of power systems over a wide range of system conditions.
Dynamic analysis provides the most accurate indication of the time responses of the system. Therefore, Dynamic analysis is extremely useful for fast voltage collapse situations, such as loss of generation and system faults, especially concerning the complex sequence of events that lead to the instability. How- ever Dynamic simulations fail to provide information such as

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1573

ISSN 2229-5518

the sensitivity or degree of stability. More importantly, dy- namic simulations are extremely time- consuming related to the CPU. Engineering resources are required for its computa- tion and analysis, in the form of differential and algebraic ex- pressions to quantify the phenomenon. [1]
Power system operation mainly depends on the interaction of three things power sources, loads and network. During a load pickup there are some events, which can induce voltage collapse via loss of a generating unit, a transmission line, or a transformer. Sometimes if the tap position setting of an OLTC is too low, it may create reverse instead of helping the system. In the case of generators, if the excitation hits its limit then it creates a considerable impact on the voltage stability.
The system stability mainly depends on its components
performance for a sudden disturbance. The responsible com-
ponents for the power system instability are non-linear e.g.
generators, motors, load devices, tap changers (controllers), etc. System stability mainly depends on the interaction be- tween the devices interconnected. That is why it is important to model all the components individually in order to have proper visualization about their performance. There are three ways to control voltage which are by adjusting the generator excitation, by using OLTC or by providing reactive power support. [1]

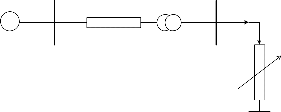
Figure 2.2.1: Model for Calculation of Real and Reactive Power flow

Similarly, for the sending end:

VSVR

2.2 Basic Principles of Active and Reactive Power Flow

Control

PS =

sin δ − Pmax sin δ

X

2

…………… (2.2.4)

Active (real) and reactive power in a transmission line depend
on the voltage magnitudes and phase angles at the sending
and receiving ends as well as line impedance. To understand
the basic concept behind the controllers a simple model is con-

Q = VS

− VSVR cosδ

X

…………… (2.2.5)

sidered in Fig. 2.2.1.The sending and receiving end voltages are assumed to be fixed and can be interpreted as points in large power systems where voltages are “stiff”. Assuming that the resistance of high voltage transmission lines are very small, there is equivalent reactance connected in between sending and receiving ends. The receiving end is modeled as an infi- nite bus with a fixed angle of 0°.
Where VS and VR are the magnitudes (in RMS values) of
sending and receiving end voltages, respectively, where δ is
the phase-shift between sending and receiving end voltages. [2, 3]
The system is assumed to be a lossless system and so the
equations for sending and receiving active power flows, PS and PR, are equal. The maximum active power transfer occurs, for the given system, at a power or load angle δ equal to 90°

SR = PR

+ jQR

= VR I

……………… (2.2.1)

which can be seen in the figure 2.2.1(b). Maximum power oc- curs at a different angle if the transmission losses are included. The system is stable or unstable depending on whether the

P = VSVR sin δ

R X

V V cosδ − V 2

Q = S R R

R X

…….. (2.2.2)

…….. (2.2.3)

derivative dP/dδ is positive or negative. The steady state limit is reached when the derivative is zero. [2, 3]
In practice, a transmission system is never allowed to oper-
ate close to its steady state limit, as certain margin must be left
in power transfer in order for the system to be able to handle
disturbances such as load changes, faults, and switching oper-
ations. The intersection between a load line representing send- ing end mechanical (turbine) power and the demand line de- fines the steady state value of δ. The angle can be increased by a small increase in mechanical power at the sending end. With increasing load demands the angle goes beyond 90° and re- sults in less power transfer. This accelerates the generator and further increases the angle making the system unstable. How- ever, the increased angle δ increases the electric power to cor- relate the mechanical increased power. The concepts of dy-

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1574

ISSN 2229-5518

namic (small signal stability) or Transient (large signal stabil- ity) are used to determine the appropriate margin for the load angleδ. [2, 3]
By the IEEE definition, “dynamic stability is the ability of the power system to maintain synchronism when subjected to a severe transient disturbance such as a fault or loss of genera- tion”. Typical power transfers correspond to power angles below 30°; to ensure steady state rotor angle stability, the an- gles across the transmission system are usually kept below 45°. Inspecting the equations carefully reveals that the real or active power transfer depends mainly on the power angle and also reactive power requirements at sending and receiving ends. The both ends typically require high power transfers. Hence it is evident that the reactive power transfer depends mainly on voltage magnitudes, which flows from the highest voltage to the lowest voltage, while the direction of active power flow depends on the sign of the power angle.
[2, 3]
Another interesting observation is the dependability on
reactance. The maximum power transfer Pmax and the angle
between two ends vary on variation of reactance. The regula- tion of power flow is also possible by varying the sending and receiving end voltages. For a given power flow, a change of “X” also changes the angle between the two ends. Regulating the magnitudes of sending and receiving ends voltages, VS and VR, respectively, can also control power flow in a trans- mission line. From the equations of active & reactive power
2.2.4 & 2.2.5 respectively, it can be emphasised that the regula-
tion of voltage magnitude has much more influence over the
reactive power flow, than the active power flow. [2, 3]

2.3 Classification of Power System Stability

There are two types of power system stability rotor angle stability and voltage stability. The power system stability clas- sified based on time scale and driving forces which is tabulat- ed in table 2.3.1. Based on time scale, stability is divided into short-term (few seconds) and long term (few minutes) stabil- ity. Also stability is classified as load driven or generator driv- en based on the instability driving forces. [1]
The rotor angle stability is classified as small-signal and
transient stability. The small signal stability deals with small disturbances in the form of un-damped electromechanical os- cillations. The transient stability is initiated by large disturb- ances due to lack of synchronizing torque. The angle stability time frame is the electromechanical dynamics of the power system. The dynamics of the time frame typically last for a few seconds. For this reason, it is called short term time scale. Time scale of short-term voltage stability and rotor angle stability is the same. But sometimes it is difficult to differentiate between short-term voltage stability and rotor angle stability. There are two types of stability problems emerged in the long-term time scale based on frequency and voltage. The long-term voltage stability is characterized by the actions of the devices such as delayed corrective actions and load shedding. [6]

Table 2.3.1 Power System Stability Classification

Table 2.3.2 Power System Component and Load Classifications

Voltage stability is also termed as load stability because it occurs due to load dynamics. On the time scale of load dynam- ics voltage stability is divided into instantaneous, short term and long-term voltage stability. Table 2.3.2 shows the system components that affect the instantaneous, short-term and long- term stability. Network and static loads are known as instan- taneous components of the system. Because they response immediately to changes occurred in the system. Short term voltage stability depends on the performance of the various components such as excitation of synchronous generator, in- duction motor, switching capacitors and static var compensa- tors (SVC) and flexible AC transmission system (FACTS). Long-term voltage stability depends on the slow responding components such as OLTC, OXL, thermostatic loads. [1]
In order to analyze voltage stability, it is worth in segregat- ing the voltage stability into small and large disturbances.
Small disturbance voltage stability controls voltage after small disturbances, e.g. changes in load.
The small disturbance voltage stability is investigated through steady state analysis. Here , the power system is linearized around an operating point. And the analysis is typically based on the eigenvalue and eigenvector techniques.
Large disturbance voltage stability is associated with the re- sponse of the power system to large disturbances such as faults, or sudden loss of load or sudden loss of generation. Large disturbance voltage stability can be used to study non- linear time domain simulations in short-term time frame and

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1575

ISSN 2229-5518

also in long-term time frame. Load flow analysis along with non-linear time domain simulations can be used to study large disturbance voltage stability. The combinations of both linear and non-linear tools are mainly used in a voltage stability problem. [1]

Power system stability is dependent mainly on the degree of maintaining the synchronism of the whole system. Out of the all blackouts round the globe the primary reasons for the blackouts is observed to be voltage collapse.

2.4 Some of the Power System Voltage Collapse & Blackouts. [11]

In 2012
On 14 January, a 380 kV transformer failure in Bursa Natu-
ral Gas Fueled Combined Cycle PP in Turkey, was accused of
voltage deviations in the interconnected power grid that re-
sulted in a blackout. Additionally, another failure occurred in
154 kV Babaeski substation caused blackout in Trakia. During the outage 6 cities in the Marmara Region of the country or more than 20 million people were affected. The power was back in all cities in the evening. The blackout knocked out met- ro and tram operation in Istanbul. Also gas heating systems didn't worked during the blackout. Industrial production was hurt badly too. The problem resolved by getting electricity from Bulgaria to Trakia and feeding lines in İstanbul from Ambarlı Natural Gas PP in İstanbul.
On 4 April, a blackout hit every city in Cyprus after the
Dhekelia power station failed (with a lack of electric power
from 04:42 to 09:20).
On 29 June, a line of thunderstorms with hurricane-force
winds swept from Iowa to the Mid-Atlantic coast and knocked
out power to more than 3.8 million people in Indiana, Ohio,
West Virginia, Pennsylvania, Maryland, Virginia, Delaware,
North Carolina, Kentucky, and metropolitan Washington, DC.
On 30 July, due to a massive breakdown in the northern
grid, there was a major power failure which affected seven
north Indian states, including Delhi, Punjab, Haryana, Hima-
chal Pradesh, Uttar Pradesh, Jammu and Kashmir, and Raja-
sthan.
On 31 July, the July 2012 India blackout, which is being
called the biggest ever power failure in the world, leaves half
of India without electricity supply. This affected hundreds of
trains, hundreds of thousands of households and other estab-
lishments as the grid that connects generating stations with customers collapsed for the second time in two days.
On 29–30 October, Hurricane Sandy brought high winds and coastal flooding to a large portion of the eastern United States, leaving an estimated 8 million customers without pow- er. The storm, which came ashore near Atlantic City, New Jer-
sey as a Category 1 hurricane, would ultimately leave scores of homes and businesses without power in New Jersey (2.7 mil- lion), New York (2.2 million), Pennsylvania (1.2 million), Con- necticut (620,000), Massachusetts (400,000), Maryland (290,000), West Virginia (268,000), Ohio (250,000), and New Hampshire (210,000). Power outages were also reported in a number of other states, including Virginia, Maine, Rhode Is- land, Vermont, and the District of Columbia.
In 2013
On 8-9 February, some 650,000 homes and businesses in the
northeastern US lost power as the result of a powerful
nor'easter that brought hurricane-force wind gusts and more
than two feet of snow to New England.
On the first of April 2013, 100 000 people in Poland suffered
under power outages due to heavy snow falls. Warsaw Air- port found the snow a bit difficult to operate in.

2.5 Various Voltage Stability Analysis Methods

Voltage stability is a attempt of load dynamics to restore power consumption beyond the capability of the combined transmission and generation system. The controllers have their own limitations. Voltage can be maintainable at desired limits under normal situation. In a particular situation arising during operation of the power system viz. major outages or large de- mand, the controllers may reach their functional limits. The voltage stability problem associated in such case requires proper attention when there is increase in demand load and exploitation of the power transmission system. An abrupt voltage collapse can happen. Hence, continued monitoring of the system state is required. The main reason behind such col- lapse is insufficient reactive power at the weak buses. An addi- tional reactive power support may be fed to the system either by fixed or switched capacitors, the voltage instability may be overcome. [1]
In a optimal impedance solution, a voltage collapse proxim-
ity indicator on power system load buses has been proposed.
The indicator performance is investigated for two types of load increment, viz. the load increase at a particular bus and the load increase throughout the system. During a single load var- iation in the system the indicator can provide a good indica- tion about the maximum possible power that could be deliv- ered to the load. On the other hand, the indicator does not ac- curately predict the maximum possible power when the load in the entire system is increased than the single load variation. [4]
The method exist which identifies those areas that experi- ence voltage collapse and also identifies the equipment outag-
es that cause sectional voltage collapse. This method deter- mines the series of events that cause the voltage collapse a con- tingency due to clogging voltage instability, Stemming from an increased transfer, wheeling or load pattern or loss of control voltage instability owed to equipment outages. This method requires little computation and is comprehensive in finding all regions/sections with voltage collapse in each region. In large AC/DC systems the implementation of both point of collapse (POC) and continuation is another method for the computation of voltage collapse points. [4]
There are other methods that analyze voltage stability, such as, model analysis using snapshots, test function, bifurcation theory, energy function methods, bus participation method, singular value method, optimization techniques, quasi steady- state method and the index method.
Tracking stability margins is a demanding problem because
of its nonlinearity nature. The SMART Device estimates the proximity of voltage collapse. In this method we use local

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1576

ISSN 2229-5518

measurements like bus voltage and load currents. This method determines the relative strength and weakness of the transmis- sion system connected to a particular load bus precisely an evaluation method. It produces an estimation of the strength/weakness of the transmission system connected to the estimated transmission capacity based on local measure- ment. SMART Device is the stability monitoring and reference setting device. The operating principle is, at the voltage col- lapse point the magnitude of the Thevenin impedance is equal to the magnitude of the load apparent impedance. Thevenin impedance is the Thevenin equivalent of the network as seen from the local substation. In this method Thevenin equivalent impedance is obtained from some locally measured data. [1]
The system operates within an adequate security margin by
estimating the maximum permissible loading of the system.
In-order to determine the maximum permissible load (static
voltage stability limit) of a power system P-V and Q-V curves are used. Bonneville power administration uses the conven- tional P-V and Q-V curves as a tool for assessing the voltage stability of the system. The P-V and Q-V curves are nonlinear at the maximum permissible power point. At maximum per- missible power point the gradient of the curves changes sign. Therefore, without practically generating the entire curves the critical load estimation by using information at a particular operating point may not lead to the correct result. To over- come this, a simple method has been proposed to estimate the critical load at the verge of voltage collapse based on V-I char- acteristic. This method requires present data for bus voltage and current. It also requires some past operating points of the system. These bus voltage and current data are readily availa- ble in all power system to prepare the V-I characteristic. The voltage and current data are processed through the least squares method to generate the V-I characteristic. The extrapo- lated part of the characteristic is then used to estimate the criti- cal load at the verge of voltage collapse. This method does not require the knowledge on other system parameters or system wide information, which makes easy to use this method. [5]
A stability factor method identifies the critical lines instead of critical buses of a power system. The stability factor method was compared with three prevailing established methods. The first method is the Lee’s method of stability. It uses stability margin as voltage stability criterion to determine whether the system is stable. The bus that has a stability margin closer to zero is considered as critical bus. The second method is the Kessel’s stability indices method. This method computes the stability index of each bus in the system and identifies the high index value bus as critical ones. The third method is the Schluster’s stability indicators method which is developed based on the changes in the load flow Jacobian. The stability indicator is a measure of the proximity to voltage collapse. It is determined from the eigenvalues of the load flow Jacobian. The eigenvalues are estimated for all load buses. The buses should have larger eigenvalue in a secure voltage control area. For the critical bus the eigenvalue decreases to less than unity which could be the origin of voltage collapse. [1]
Global positioning systems (GPS) can economically synchro- nize the sampling process at a distant substation . Phasor measuring unit (PMUs) is the basic hardware box that converts current and voltage signals into complex phasors. It is a ma- ture tool now which uses synchronization signals from the GPS satellite systems. Protection and control systems limit the impact, stop degradation and restore the system to a normal state at the time of major disturbance by using appropriate corrective actions when needed. Wide area measurement and protection system recognize, propose and execute the coordi- nated stabilizing actions, which helps to limit severity of dis- turbances. A system design has been proposed based on the synchronized phasor measurement units, encouraging system protection schemes for frequency, angle and voltage instabili- ties.
There is no simple way to identify the location of the critical
node and the critical transmission path. Some of the methods check the system’s Jacobian matrix to determine the critical node. This needs computation to estimate real-time voltage stability. However, voltage phasors contain enough infor- mation to detect the voltage stability margin of a power sys- tem. To identify the critical transmission paths with respect to the real or reactive power loading based on the voltage phas- ors approach, a voltage collapse proximity index has been proposed. In this method, the difference between the halved voltage phasor magnitudes of relevant generator considered as transmission path stability index as well as the voltage drop along the transmission path. Two types of transmission paths were proposed. Those are active transmission path and reac- tive power transmission path. Active transmission path is a sequence of connected buses with declining phase angles start- ing from a generator bus. Reactive power transmission path is a sequence of connected buses with declining voltage magni- tudes again starting from a generator bus. In this method, the power transfer on that transmission path becomes unstable due to voltage collapse if the value of transmission path stabil- ity index reaches zero. [5]

2.6 Influence of Different Power system components on

Dynamic Voltage Stability

Usually slower acting devices and fast-acting devices contrib- ute to the evolution of voltage collapse due to sudden disturb- ances in the power system. On load taps changers, generator over excitation limiters, characteristics of the system loads are considered slower acting devices. Induction motors, excitation system of synchronous machines and compensation devices are considered fast acting devices. [7]
Tap changers in main power delivery transformers are the
main mechanisms to operate and regulate the voltage automat- ically. Tap changers control the voltage by changing the trans- former turns ratio. In many cases, the variable taps are placed on the high voltage side of the transformer. The reason for that it is easier to communicate. Various acronyms have been sug- gested for the transformer tap changer mechanisms. Those are on load tap changers (OLTC), under load tap changers (ULTC), tap changers under load (TCUL), and load tap chang- ers (LTC). [7]

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1577

ISSN 2229-5518

There are two types of tap changer models which are very common to use. Those are continuous type and discrete type. Continuous models are based on the assumption of continu- ously changing taps. Discrete models are based on the discon- tinuous or step-by-step tap change. A typical transformer equipped with an OLTC feeds the distribution network and maintains constant secondary voltage. OLTC operates with a certain delay. It depends on the difference between the refer- ence and actual voltages at OLTC input. The phenomenon of raising the position of on-load tap changer for raising the sec- ondary voltage causes the drop of secondary voltage. The sec- ondary voltage of a transformer maintains a level higher than its lower bound by automatic OLTC even if the voltage of pri- mary transmission system drops. However, the secondary voltage becomes unstable if the load demand becomes exces- sive. The instability of tap changer happen when the load de- mand is increased other than kept constant. The reverse action of the tap changer could occur when the initial operating volt- age in the secondary side of the transformer is far less than the rated value. The effects of OLTC transformer on voltage stabil- ity and the identification of the critical OLTC transformer in a general power system have been studied. [7]
Synchronous generator is the primary device for voltage and
reactive power control in power system. The most important
reactive power reserves are located in the synchronous genera-
tor. Active and reactive power delivering capabilities of gener-
ator are required to achieve the best results in voltage stability studies. The generator may lose their ability to act as a constant voltage source because of the high reactive power demand by the loads and the field current limits. For such case the genera- tor terminal voltage reduces and it behaves like a voltage source behind the synchronous reactance. In 1986,
K. Walve first suggested the effect of excitation system limits
on voltage stability. The power system may become unstable
due to lack of reactive resources if the generator hits the reac-
tive power limits. The reactive power output of a generator
reaching a limit has two causes: excitation current limit and the
stator current limit. Two types of excitation current limits are
reason it is very difficult to model exact loads. The main prob- lem is to identify the load composition at a given time. The differential equations for induction motors, tap changing near static load and heating system are non-linear. It is very diffi- cult to parameterize for model estimation. A nonlinear model was proposed based on the assumption of exponential recov- ery. To obtain the dynamic voltage stability limit of a power system the first-order variable admittance model and the ag- gregate nonlinear recovery model have been considered along with the system dynamic equations. Third order induction motor model is another model to represent the induction mo- tor loads. [1]
A short circuit in a network reduces the voltage. It also re-
duces the electrical torque developed by an induction motor.
As a result the motor decelerate occurs. The speed reduction or
slip increase of induction motor depends on the mechanical
torque demand and motor inertia. During the short circuit, induction motors absorb a greater amount of reactive power. It operates at low factors which may further decrease the voltage and finally stall the motors.
From the viewpoint of dynamic phenomena, the voltage collapse starts locally at the weakest bus and spreads out to the
other weak buses. [1]

3 MATHEMATICAL MODEL

Voltage instability is a structural instability of system caused by variation of numerous parameters. This chapter describes the mathematical model that is used in voltage stability studies and the assumptions that are used in this project’s analysis.

3.1 Determination of LVSI

3.1.1 Two-Bus System

Fig 3.1.1 shows a simple two bus system where the source bus
‘I’ is connected to the load bus ‘j’ through a transmission line.
It has an impedance of Z line . The current I flows through the line as well as through the load impedance (Z l ). The complex
over excitation and under excitation limit. To avoid stator overloading, stator current limit is used to limit reactive power output. But the action of the stator current limit is not good for voltage stability. The stator current limiter decreases the reac- tive power capability to avoid stator overheating. As a result voltage decreases dramatically. It is important for voltage sta- bility to have enough buses in a power system where voltage may keep constant. The excitation/automatic voltage regula- tor (AVR) system limits of synchronous generators are the
voltages considered as buses ‘I’ and ‘j’ [1]

Vi ∠δ i

Vi ∠δ i

Z line

V ∠δ

and j , respectively at

V j ∠δ j

most important for fulfilling that need. The AVR keep voltage constant. In some cases field current limitation introduces slow generator dynamics that interact with the long-term dy- namic devices, such as OLTCs. In other cases the generator dynamics remain fast even after the limitation of rotor current. [3]
Loads are the driving force of voltage instability. So, volt-
age stability is also called load instability. Loads are aggrega-
tion of many different devices in the power system. For this

Bus i Bus j

Z l

Figure 3.1.1 Simple two bus system to determine LVSI

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1578

ISSN 2229-5518

According to the maximum power transfer theorem, when the
magnitude of load impedance (Z l ) becomes equal to the mag-

3.1.2 Two-Bus System with a off-nominal Tap setting

Transformer

Consider an off nominal tap setting transformer with an im-
nitude of the line impedance ( Z line ), the system reaches the
maximum power point or the critical point at which the volt-
pedance of (Z T

) is connected between bus ’I’ (source bus) and

age collapse occurs. Thus, at voltage collapse point
bus ‘j’ (load bus). Fig. 3.1.2.2 shows the connection.

Z ij ,

Z ij1 ,

Z line

= Z l
………... (3.1.1.1)

Z ij 2 are equivalent mutual impedance, shunt impedance on

side ‘I’ and side ‘j’ respectively in the equivalent π circuit
The magnitude of voltage drop across the transmission line is less than the magnitude of load bus voltage under normal
condition. When the system reaches its maximum power trans-
model of the transformer which is shown in the Fig. 3.1.2.1 If the off-nominal turns ratio of the transformer is a: 1,
fer level, the magnitude of voltage across the transmission line becomes the same as the magnitude of load bus voltage. There- fore within the voltage stability limit, the relationship between

Z ij

,

Z ij1

and

Z ij 2

are given
the load voltage and voltage drop can be written as

Z ij

= (a)ZT

………… (3.1.2.8)

Vi − V j

≤ V j

……….. (3.1.1.2)
Equation (3.1.1.2) is in the form of complex variables. The magnitude form of equation 3.1.1.2 is



Z ij1 = 

a 2

1 − a



Z T

V 2 + V 2 − 2V V Cos(δ

− δ ) ≤ V 2

  ………… (3.1.2.9)

i j i j

i j j

……….. (3.1.1.3)
By solving the inequalities:-



ij 2 

a 

ZT

V 2 − 2V V Cos(δ

− δ ) ≤ 0

 a − 1 

……………. (3.1.2.10)

i i j i j

Or
…………. (3.1.1.4)
When the off nominal turns ratio of the transformer

V j

2 Cos(δ i − δ j ) − 1 ≥ 0

is 1: a,

Z ij

,

Z ij1

,

Z ij 2

become

Vi ………….. (3.1.1.5)

Z ij = (a)ZT

………… (3.1.2.11)

V = V δ = δ

At no load condition, j and angle j . Thus, the
left hand side (LHS) of equation (3.1.1.5) becomes unity. Under

Z =  a Z

ij1  a − 1  T

normal operation (between no load and the maximum load) LHS of equation (3.1.1.5) will be greater than zero but less than unity. At the maximum loading condition (voltage collapse) it becomes zero. From the above reasoning, the voltage stability





Z ij 2 = 



a 2 

Z T

…… (3.1.2.12)
index of the line at bus ‘j’ (LVSI j ) can be expressed as follows

V j

 1 − a 

… (3.1.2.13)

Vi ………….. (3.1.1.6)

Vi ∠δ i

ZT

V j ∠δ j

I

Similarly, LVSI i at bus ‘I’ can be expressed as

Vi

Transformer

Bus i Bus j

l

LVSI i = 2

V j

Cos(δ j − δ i ) − 1

…………. (3.1.1.7)


The magnitude of LVSI j and LVSI i depends on the direction and the amount of power flow.

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1579

ISSN 2229-5518

Figure 3.1.2.1 Simple two-bus system with transformer having off nominal turns ratios

Vi ∠δ i

The Thevenin equivalent circuit of the system (fig 3.1.2.2) is shown in fig 3.1.2.3. It is similar to fig 3.1.2.1. By replacing

Vi

Z ij

V j ∠δ j

Vi by

aVi

for 1:a off nominal turns ratio or a

LVSI j

for a:1 off-

Bus i Bus J

nominal turns ratio
and LVSI i
of fig 3.1.2.3 can be

Z ij1

Z ij 2

Z l

evaluated for equations (3.1.1.6) and (3.1.1.7) respectively. [1]






Figure 3.1.2.2 Equivalent circuit of Fig 3.1.2.1
Replace the generator and the transformer by Thevenin equiv- alent circuit. The source at bus ‘I’ is considered as ideal i.e. constant voltage with zero source impedance. With an off nominal transformer the parameters of the Thevenin equiva- lent circuit ( Z th , Vth and δ th ) with turns ratio a: 1 are

Z ij Z ij 2

3.1.3 LVSI of a transmission line in a General Power System Equations (3.1.1.6) and (3.1.1.7) don’t require the generator, load and line parameters. Those equations only require the complex bus voltage to evaluate the line voltage stability in- dex. This simple requirement can be used to evaluate the volt- age stability index of a transmission line in a general power system as shown in Fig. 3.1.3.1 It requires only the complex voltage at buses ‘I’ and ‘j’ at both ends of the line. LVSI at bus

‘J’ side and LVSI at bus ‘I’ side can be determined using the
expressions (3.1.1.6) and (3.1.1.7) for the transmission line be-

tween buses ‘I’ and ‘j’ which is shown in Fig 3.1.3.1.

Z th = Z ij || Z ij 2 =

Z ij + Z ij 2

…….(3.1.2.14)

Rest of the system

Vi

Vth =

Z + Z

Vi

Z ij 2 =

a

ij ij 2 …….(3.1.2.15)

When the effect of transformer resistance is neglected, the an- gle δ th will be the same as δ i

Line

Bus i Bus j

δ th = δ i

…….. (3.1.2.16)

Figure 3.1.3.1 Transmission line connected between buses ‘I’ and ‘j’

Similarly for transformers with 1: a off nominal turns ratio, the

in a general power system

expression for Z th and δ th remain the same but Vth
to

Vi

is changed

3.1.4 Determination of VSI of a General Power System

Power system networks are mesh type thus it is important to determine the VSI of a mesh network. First compute the LVSI of the network at both ends of all branches (lines and

Vth =

Z ij 2 = aVi

Z ij + Z ij 2 .……. (3.1.2.17)

transformers) using load flow results. Power flows from higher
LVSI to lower LVSI in a branch. Higher LVSI side considered as stronger side or upstream side while the lower LVSI side considered as weaker side or downstream side. Based on the

Vth ∠δ th

Z th

V j ∠δ j

LVSI j

LVSI

and i , the mesh network decomposed into a

Bus i Bus j

Z l

Figure 3.1.2.3: Equivalent circuit of Figure 3.1.2.2

number of power flow paths.[1]
Identification of power flow path starts at a source bus or
upstream side and proceed to all downstream side buses
which are connected through a branch. The upstream side has higher value than that at the downstream side. If the branch has lower LVSI at the upstream side than that at the down- stream side, it should not be considered in the path. The above process is to be continued until it is found that no additional branch can be added to the path because of having lower LVSI at the upstream side compared to the downstream side. [1]

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1580

ISSN 2229-5518

Start the identification of power flow paths at bus 1 which

1.0756 L2

3

is connected to bus 2, bus 3 and bus 8 via lines

L1 ,

L2 and 1

L11 respectively. Line

L1 has a LVSI of 0.9881 (near bus 1) and

1.0148 0.9881

0.9054

0.9824

0.9504(near bus 2). Since LVSI in the upstream side (bus 1) is higher than that at the downstream side (bus 2), the line

L11 L1

L3

1.0978

should be included in the path. Similarly line L2
and

L11

L12

should be included in the path. Now start at bus 2 which is connected to bus 4 and bus 6 through L13 and L10 . These lines have higher LVSI at the upstream side compared to the down-
stream side thus these lines should be included in the path.

0.9504

2

1.0782

1.0792

L13

0.9223

1.0178

4

0.9871

Bus 6 connected with bus 10 through

L6 which has a LVSI of

0.9766 L4

8 1.0011

0.9988 (near bus 6) and 0.9967 (near bus 10). Since LVSI in the
upstream side (bus 6) is higher than that at the downstream side (bus 10), the line should be included in the path. Now bus
4 is connected to bus 5 through L4 that has lower LVSI (0.9871) at the upstream side (bus 4) compared to the downstream side (1.0011 at bus 5) thus it should not be included in the path. In this case path terminates at bus 4 as shown as Fig. 4.1. This technique is to be repeated to identify the other possible power flow paths of the system. After identifying the all possible power flow paths need to calculate PVSI of each power flow path. PVSI can be written as

L10 5

0.9235

6

0.9988

6

0.9204

10

PVSI = P LVSI kj

k =V ………….. (3.1.4.1)

Where Ϛ is a set of lines that constitute a power flow path and j is the downstream side of the line. PVSI considered as the most heavily loaded path or critical path that is vulnerable to voltage collapse. The value of PVSI of the most heavily loaded path is considered as the overall stability index of the system. [1]
The voltage stability index (VSI) of the power system is ex- pressed as follows

Figure 3.1.4.1: Power flow path identification

4 APPLICATION OF MATHEMATICAL MODEL

Voltage magnitudes and angles of all the buses of the test sys- tem at base condition are given in table 4.1. Using the result of base case load flow the LVSI at both ends of all branches are computed through equations (3.1.1.6) and (3.1.1.7) and the values found are mentioned in Fig. 4.1.

VSI = min(PVSI m )

..…….. (3.1.4.2)
Where m varies from 1 to n and n is total number of possible power flow paths originating from buses.

Table 4.1 IEEE 10 Bus System, Bus Voltage and Angle at Base Load

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1581

ISSN 2229-5518

After identifying the all possible power flow path it is required to calculate the PVSI of each power flow path.The PVSI of all power flow paths are evaluated using equation 3.4.1. Consider Path P1 as shown in Table 4.2 which starts at bus 1 and termi- nates at bus 10. The immediate buses are bus 1,2,3,8,9, and 10.
The lines that constitute the path are

L1 , L2 , L11 , L8 , L9 . Thus

1.0756

L2 0.8495

the set Ϛ is { L1 , L32 , L11 , L8 , L9 }. The PVSI of the path can be
alculated as

1.0148

c

0.9881

0.9054

0.9824

PVSI P1

= (LVSI

L 2 ,3

L

× LVS L 2,3

× LVSI

L11,8

× LVSI

L8,9

× LVSI

L9,10 )

L11 L1

= 01.0.9758 04 X 0.8495 X 0.9766 X 0.9221 X 0.9204

12

= 0.669177
The results of PVSI are tabulated in Table 4.3.

0.9504

2

1.0792

L13

0.9223

1.0178

Table 4.31.P07V82 SI Values of All the 4Power Flow Paths

0.9871

0.9766

8

Path
No PVSI

L10

L4

1.0011

5

1.0789

L8

P10.9235
P2 6

0.9988

P3
0.6692
0.6694

L6 0.7272

0.9298

L5

1.0726

7

0.9204 0.9204

0.9967 1.0795

L7

0.9221

Out of all the powe0.r922f6low paths

P1 has the minimum PVSI

9 ( L9

10

. Hence th critical path at base load condition is the
0.6692) e
Path

P1 (1, 2, 3, 8, 9, and 10). The last bus of the critical power

Figure 4.1 IEEE-10 bus test system

The above technique which discussed at section 3.1.4 is used repeatedly to identify the other possible power flow paths of the system. All power flow paths that start at bus 1 are given in Table 4.2.
flow path is considered as the weakest or critical bus in the system. The branch in the critical power flow path that has the higher value of LL id considered as the most heavily loaded branch. At the base condition, bus 10 is identified as the critical bus because it is the last bus of the critical power flow path ( P1 ). The values of LL of all lines in the identified critical power flow path ( P1 ) are given Table 4.4 which indicates that
line

L2 connected between bus 1 and bus 3 has the highest

value of LL (0.2261). Hence line L2
line.
is identified as the critical

Table 4.2 Power Flow Paths Starting From bus 1 at Based Load

Table 4.4 Values of All the Lines in the Identified Critical Power

Flow Path

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1582

ISSN 2229-5518

Generator

5 CONCLUSION

The voltage stability of the system can be expressed in voltage stability index of the system. The voltage stability index (LVSI) is calculated for all lines. The LVSI is compounded to deter- mine path voltage stability index (PVSI) through possible power flow path of all permutation in the network. The power flow with minimum (PVSI) is the critical power flow path of the system and the critical line is demarcated by LVSI of all lines in the critical power flow path.

APPENDIX

[A] Glossary of Terms

System –A combination of generation, transmission, and distribution elements. Reliability – A measure of how often electrical service is interrupted.

Load – An amount of end-use demand.

Grid – Usually used to describe the interconnected transmission system, although

sometimes used with distribution (distribution grid) to describe the distribution system.

Electricity – The flow of electrons through a conductor. Generation – The creation of electricity.

Current – The rate of flow of electrons through a conductor.

Demand – The total amount of electricity used at any given moment in time,

usually measured in KW or MW

Deregulation – The process of decreasing or eliminating government regulatory

control over industries and allowing competitive forces to drive the market.

Distribution – The delivery of electricity over medium and low-voltage lines to

consumers of the electricity.

Base load – Electricity usage that is constant through a specified time period. Also used to refer to the generating units that run all 24 hours of the day to serve a system’s base load demand.

Blackout – The loss of power to a portion of the distribution or transmission sys- tem.

Circuit – A complete path through which electricity travels, comprised of sources

of electrons, energy consuming devices and conductors.

Circuit breaker – A device that interrupts electricity flow to a circuit by isolation

the circuit from the source of electricity.

Stability Limit – The maximum power flow possible through some particular

point in the system while maintaining stability in the entire system or the part of

the system to which the stability limit refers.

Stability – The ability of an electric system to maintain a state of equilibrium

during normal and abnormal conditions to which the stability limit refers.

Disturbance – 1. An unplanned event that produces an abnormal system condi-

tion. 2. Any perturbation to the electric system.

[B]

Base case data Load

Transmission Lines

ACKNOWLEDGMENT

We the authors are thankful and ever will be to Dr. D.B. Ojha and Shri Arvind Sharma, faculties at Mewar University, for their valuable guidance, support and encouragement while preparing this paper and bringing it to this level.
We also extend our thanks to Shri A.S.Abhinav, a pre-final year student of Electrical & Electronics Engineering, RGP Uni- versity for his whole hearted support and providing the all necessary help at the moment when it was required the most.

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 1583

ISSN 2229-5518

REFERENCES

[1] UMAMAHESWARA RAO POTHULA, “STATIC AND DYNAMIC VOLTAGE STABILITY ANALYSIS”, LAMBERT ACADEMIC PUBLISHING AG & CO. KG,

201.

[2] N.G.HINGORANI, LASZLO GYUGYI “UNDERSTANDING FACTS

CONCEPTS & TECH NOLOGY OF FLEXIBLE AC TRANSMISSION SYSTEM”

ISBN-81-86308-79-2.

[3] Prabhakar Kundur “ Power syayem stability & control”

ISBN-13-978-0-07-063515-9 & ISBN-1-0—07-063515-3.

[4] G.K.Morison, B.Gao, P. Kundur, “Voltage Stability Analysis Using

Static and Dynamic Approaches, IEEE Transactions on Power Sys- tem,Vol. 8, No. 3, pp 1159-1171 August 1993.

[5] Venkataramana Ajjarapu, Colin Christy, “ The Continuation Power

Flow: A Tool For Stady State Voltage Stability Analysis”, IEEE Transac-

tions on Power Systems, Vol. 7, No. 1,pp 416-423, February 1992.

[6] C.W. Taylor, “Power system voltage stability”, New York: MCGraw- Hill, 1994.

[7] D.Novosel, M.M.Begovic and V. Madani, “Shedding light on blackouts”, IEEE Power and Energy Magazine, Vol.2, No.1,pp 32-43, Jan/Feb 2004.

[8] Chandrabhan Sharma, Marcus G. Ganness, “Determination of Power

System Voltage Stability Using Modal Analysis”, IEEE Xplore, April

2007.

[9] Nguyen Tung Linh, “Voltage Stability Analysis of Grids Connected

Wind Generators”, IEEE Xplore, 2009.

[10] G. Giadrossi, R. Menis, G. Sulligoi, A. Tessarolo, “Voltage Stability

Analysis of All-Electric Cruise Liners”, IEEE Xplore, 2008. [11] Wikipedia “List of major power outage”.

————————————————

• Author A.S.Ravi PH-+91-9869620990/022-28264309. E-mail: a.s.ravi@liv e.in and Co-Author Ashutosh Dwivedi PH- +91-9451139348. E-mail: ashudwivedi92@gmail.com & Bhuvan Sharma PH- +91-9760539863. E-mail: bhuvan_sharma123@yahoo.co.in are currently pursuing MTech Electrical En- gineering (Power System) in Mewar University, India.

IJSER © 2013 http://www.ijser.org