International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 1

ISSN 2229-5518

Using Continuous Feature Selection Metrics to

Suppress the Class Imbalance Problem

P. Ganesh Kumar, J. Briso Becky Bell

Abstract— The class imbalance problem is a serious problem in machine learning that makes the classifier perform suboptimal during data classification. Among the many competent approaches, feature selection is well suited for suppressing the class imbalance problem. In this paper four continuous feature selection metrics namely Pearson Correlation Coefficient (PCC), Signal to Noise Ratio (S2N), Feature Assessment by Sliding Threshold (FAST) and Feature Assessment by Information Retrieval (FAIR) are developed for producing feature sub sets from a small sample datasets and are then evaluated using Support Vector Machine (SVM) classifier. Various Cancer datasets available in the National Center for Bioinformatics (NCBI) are used in the experiments. Simulation results using these datasets show that the proposed system selects highly relative features and has high classification accuracy. Statistical analysis of the test result shows that among the four continuous feature selection metrics, the FAST metric shows relatively better result than the others.

Index Terms— Class Imbalance Problem, Datasets, Feature Selection, Genome, Hyper-plane, Microarray, Support Vectors.

——————————  ——————————

1 INTRODUCTION

HE class imbalance problem [1] is a difficult challenge faced by machine learning and data mining community, a classifier model affected by this problem would see strong overall accuracy but reduces the poor minority class’s performance for specific datasets. This problem occurs in two different types of datasets namely Binary class and Multi class datasets. The former occurs where one of the two classes is comprised of considerably more samples than the other, where as the latter occurs when each class only contains a tiny fraction of the samples. Datasets meeting one of the two above criteria have different misclassification costs for the different classes. There are a large number of real-world applications [2], [3] that give rise to datasets with an imbalance in classes. Examples of these kinds of applications include medical diagnosis, biological data analysis, text classification, image classification, web site clustering, fraud detection, risk
management, automatic target recognition, and so on.
There are many techniques to combat the class imbalance
problem. They fall in one of the three approaches namely Re-
sampling, New Algorithms and Feature Selection. Re- sampling methods [4] strategically remove majority samples
and add minority samples to an imbalanced dataset to bring the distribution of the dataset nearer to the optimal distribution. New algorithms [5] approach the imbalanced problems differently than standard machine learning algorithms; these include one-class learners [6], bagging and boosting methods [7] and cost-sensitive learners [8]. Feature selection method [9] selects a small subset of the original feature set to reduce the dimensionality of the dataset and facilitate better generalization of training samples.

————————————————

 P. Ganesh Kumar is currently working as assistant professor in information technology in Anna University of Technology Coimbatore, India, PH-+919789990889. E-mail: ganesh23508@gmail.com

 J. Briso Becky Bell is currently pursuing masters degree program in information technology in Anna University of Technology, Coimbatore, India, PH-+919677890458. E-mail: brisobell@gmail.com

Feature selection is one technique which is well suited for class imbalance problem, since it selects a subset of features so to be induced by classifier to reach an optimal performance. On Foremen [10] found that clever induction cannot be made accurately when there is a lack of productive input space, which shows that in high-dimensional datasets feature selection alone can combat the class imbalance problem.
In order to solve the class imbalance problem many feature selection methods were experimented, when Elkan [11] found that some of the applied feature selection methods did not consider some highly correlated features, as most of the features selected were thought to be redundant. Then the serial problem was most of the researchers thought that selecting highly relevant features were only useful, but Guyon and Elisseeff [12] showed that irrelevant features on their own can be useful in conjunction with other features, and the combination of two highly correlated features can be better than considering any of the one feature separately.
Loughrey and Cunningham [13] considered a feature interaction in the selection process, using Wrappers and embedded methods as subset feature selection methods. But this method the subset found is severely over-fits the training data and causes much worse performance than the baseline performance. And they cannot find the best feature subset as the algorithm has high runtime for selecting the optimal feature set and it is inflexible for high-dimensional data. Whereas Guyon and Elisseeff [12] found that by using feature selection metrics on high dimensional data sets avoids both of these problems, as these metrics are robust against over-fitting and considerably has a linear runtime with the size of the feature set.
Zheng et al. [14] classified the feature selection metrics in to two based on the way they access the classes. He considered the Positive features indicate the membership of a class and negative features indicate the lack of membership to a class. One-sided metrics only select positive features on their score, and two-sided metrics selects both positive and negative features based on the absolute value of their score. While

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 2

ISSN 2229-5518

Foreman [10] noted that when using evenly balanced form of Bi-Normal Separation (BNS) to select features with equal weight to true and false positive rates, gave best performance.
The overall aim of the paper is to develop four continuous feature selection metrics and to evaluate their performance by inducing the selected features in a classifier which makes the classifier to perform optimally by suppressing the class imbalance problem. The structure of the rest of this paper is described as follows. Section 2 briefly introduces about the current feature selection approaches taken to suppress class imbalance problem. In Section 3, the various experimental setups we used are presented. Details of the classification algorithms and their implementation issues are discussed in Section 4. Simulations conducted using 10 benchmark datasets and the results are reported in Session 5. Concluding remarks are given in Section 6.

2 FEATURE SELECTION APPROACHES

According to Chen and Wasikowski, [1] the current feature selection metrics are classified in to Binary and continuous feature selection metrics, by considering the way they accessed the type of data.

2.1 Binary Feature Selection (BFS)

Binary feature selection metrics [1] can handle only binary data. In binary feature selection metrics binary data is used so to ensure that no metric had an advantage because of a

2.1.3 Odds Ratio (OR)

OR [10] is a descriptive test which analyzes the occurrence of an event by considering an already occurred event. In machine learning, it is used to quantify the change in odds of a sample drawn from a class, given a feature’s values. We find the odds of a feature occurring in the positive class and normalize by the odds of the feature occurring in the negative class. Then we calculate the change in odds, OR can be either one-sided or a two-sided.

2.2 Continuous feature selection (CFS)

Continuous feature selection metrics [1] are designed to operate on continuous data and they do not require any preprocessing.

2.2.1 Pearson Correlation Coefficient (PCC)

PCC [15] is a statistical test that measures the quality and strength of the relationship between two variables. The coefficients can range from −1 to 1. The absolute value of the coefficient closer to 1 indicates a stronger relationship. The sign of the coefficient gives the direction of the relationship. If it is positive, then the two variables increase or decrease with each other, when it is negative, one variable increases as the other decreases. Here the covariance and the variances of feature (Xi) and the target (Y) are taken, then correlation can be calculated directly. It can be made as either one-sided or two sided metric. The PCC is calculated by formula given in (1).
feature’s structure as it is discrete. Because the datasets we
studied consist of continuous data, so preprocessing of data
before applying these metrics is done. Finding the mean

PCC = 1 (

N 1

X  X )(

X

Y  Y )

Y

(1)
feature value for the two classes, then set a threshold at the midpoint between the two mean values. The features are then converted into binaries according to a threshold value, so its performance is entirely dependent on the choice of the preset threshold used for converting in to binaries. This threshold determines the confusion matrix’s true positive (TP), false negative (FN), false positive (FP), and true negative (TN) counts.

2.1.1 CHI Square Test (CHI)

CHI [10] uses a statistical test for feature selection. It measures the independence of a feature from the class labels based on the confusion matrix. This happens by assuming that there is a non-zero probability for an exact value to be drawn from the

2.2.2 Signal to Noise (S2N)

The signal-to-noise ratio [1] is originally a concept in electrical engineering. It is the ratio of a signal’s power to the power of the noise present in the signal. If a signal has a lot of noise present, it is much more difficult to isolate the signal. It compares the ratio of the difference between the class means to the sum of the standard deviations for each class. For a feature, if the two class means are distant, there is a less chance of a sample to be from other class. If the class means are close, there is a high chance of mislabeling or else if the standard deviation is larger or smaller it scales the distance appropriately. It is a one-sided metric. The formula for calculating S2N is given in (2).
distribution, which leads to extremely small expected counts of feature values. It is a two-sided metric.

2.1.2 Information Gain (IG)

  

S2N = 1 1

 1   1

2.2.3 Feature Assessment Techniques

(2)
IG [14] is a feature selection metric which measures the
decrease in entropy of the class labels while using a feature.
We calculate the entropy of a random variable (class labels)
which grows as the proportion of samples approaches fully
balanced. The conditional entropy measures the remaining uncertainty for a random variable. Then we simply subtract
the entropy and conditional entropy to get IG. This measure is two-sided.
Here we slide the decision boundary, in order to increase the number of true positives and to find the expense of classifying more false positives. When sliding the threshold to decrease the number of true positives found in order to avoid misclassifying negatives. Thus, no single choice for the decision boundary may be ideal for quantifying the separation between two classes. So it is fruitful to use a feature selection metric that is a non-parametric one, thus using all possible confusion matrices states when using continuous data.

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 3

ISSN 2229-5518

Thus, it would be possible to find the threshold that result in the highest performance. There are two non parametric measures they are ROC and Precision-Recall (P-R) curves. If we calculate the area under the curve for these measures the resultant metrics are FAST and FAIR.

2.2.3.1 Feature Assessment by Sliding Threshold

(FAST)

In FAST, [15] classification of the samples based on multiple thresholds and gathering statistics on the performance at each boundary is done. Here we calculate the True Positive Rate (TPR) and False Positive Rate (FPR) at multiple thresholds using (3) & (4), for this we need to find the total number of True Positives (TP), False Positives (FP), True Negatives (TN) and False Negatives (FN) then we build an ROC and calculate the Area Under the Curve (AUC). Because the AUC is a strong predictor of performance, it is especially suited for imbalanced data classification problems. This score can be used for feature ranking, while choosing the features, take the highest AUC’s as they have the best predictive power for the dataset. The area can be found by formula (5). It is a two-sided metric.
As binary feature selection metrics needed much preprocessing in continuous data it is not the most preferred metric.

3 EXPERIMENTAL SETUP

In this paper, we compare the performance of example various continuous feature selection methods to show which of these approaches best manages the challenges posed by imbalanced data sets. We will look at the performance of different feature selection metrics on microarray. We aim to inform data mining practitioners which continuous feature selection metrics would be worthwhile to try and which they should not consider using it. While measuring the performance standards of metrics, we use certain classifiers and non parametric measures to evidently know the better performed metrics over the disease sample dataset. In order to solve the problem we developed four continuous feature selection metrics such as PCC, S2N, FAST and FAIR for to select the highly relevant feature. We also used the integrated classifiers such as SVM, K-Nearest Neighbor (K-NN) and Naïve

T PR (1   ) 

FPR (1   ) 



TP

(T P + FN)

FP

(FP + T N)

1 

(3) (4)

Bayesian to induce the test samples. We also obtained various small sample high dimensional imbalanced datasets of biological domain for to be used as input in our system. Then we developed a non parametric statistical measure to find the overall goodness of the classifiers using AUC-ROC measure.

AUC =  (1   i   )  2 1     

(5)

High Dimensional Imbalanced microarray datasets

i  

Where,

1   = (1 i )  (1 i 1 ) ,    i   i 1

2.2.3.2 Feature Assessment by Information Retrieval

(FAIR)

The major deviation of FAIR [15] from FAST was the use of P- R curve instead of the ROC as our non-parametric statistic. The PRC [16] are vastly different and strongly indicate the use

PCC Metric

S2N Metric

FAIR Metric

FAST Metric

of one algorithm over the other. This modification is called Feature Assessment by Information Retrieval (FAIR) because it uses the information retrieval standard evaluation statistics of precision and recall to build the curve. FAIR is a two-sided metrics. For the P-R curve, we simply take a parallel tabulation of the precision and recall for the majority class, build the P-R curve from these values, and take the maximum area. Precision and recall can be calculated using formulas (6)
& (7). Then area under the P-R curve can be calculated using
formula (5).

Reduced input genes

Induction method

Performance Evaluation

Precision (1   ) 

TP

(T P + FP)

(6)

Fig. 1. Architecture of the proposed system

The high dimensional imbalanced microarray datasets are input to the system and we used the continuous feature

Recall (or) T PR (1   ) 

TP

(T P + FN)

(7)
selection metrics for to select the most expressive genes. These metrics selects highly related features in a dataset forming
When comparing the binary metrics effects with the
continuous metrics. Binary metrics fully depend on single threshold value thus making the performance change in every
threshold.
reduced feature size. Then the reduced feature dataset is used to induce a classifier. And the performance of the classifiers effect on classification is measured so to assess the metrics efficiency on classification. The architecture of the proposed system is illustrated in fig.1

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 4

ISSN 2229-5518

3.1 microarray sample datasets

In the field of molecular biology, gene expression profiling [17] or microarray technology is the measurement of expression of thousand of genes simultaneously to study the effects of certain treatments, diseases, and development stages on expression. There are a variety of microarray platforms that have been developed to accomplish this and the basic idea for each is simple: a glass slide or membrane is spotted or
―arrayed‖ with DNA fragments that represent specific gene coding regions. Purified RNA is then fluorescently or radioactively labeled and hybridized to the slide/membrane. After thorough washing, the raw data is obtained by laser scanning or auto radiographic imaging. Thus the raw microarray data are images, which are transformed into m*n gene expression matrices as shown in the Table 1.
Each row in the data matrix represents a sample that
consists of m number of genes G from one experiment. Each
sample S belongs to certain class (normal/disease). In each
data set the researchers repeated the same experiment on n different volunteers, each line in this data set representing the
volunteer sample S. The numbers in each cell characterize the expression level of the particular gene in particular sample.
The Microarray datasets are affected by two kinds of serious problem, high dimensional problem and class imbalance problem. The first occurs due to the ultra high dimensionality nature of microarray data, considering a typical gene expression profiling experiment produces expression level of
2,000-30,000 genes for about 40 to 200 samples. Dimensionality reduction has drawn special attention for such type of data analysis. Among tens of thousands of genes in experiment, only a smaller number of them show strong correlation with the targeted phenotypes. Also, recent researchers have shown that the number of genes varies greatly between different diseases, a small number of genes are sufficient for accurate diagnosis of most of the diseases. Thus computation is reduced while prediction accuracy is increased via dimensionality reduction.
Secondly, the class imbalance problem occurs when the

TABLE 1

GENE EXPRESSION DATA MATRIX WITH IMBALANCED CLASSES

constraint 2x = n becomes true, where the x ranges from 1 < x
≤ n-1 is the variable that determines the number of samples in
class I as shown in table I. Further based on x’s range, the
imbalance pattern divided in to two. In case one x ranges from
1 < x ≤ (n-1)/2, then the class I becomes minority class and
class II becomes majority class and in case two it ranges
between (n+1)/2 < x ≤ n-1, then the class I becomes majority
and class II becomes minority, thus class imbalance problem
prevails due to the unequal number of samples in each of the two classes at both cases. Thus feature selection acts as remedy
for high dimensional problem also enhances in suppressing the class imbalance problem.

3.2 Classification Schemes

Classification [18] is a two step process containing model construction and modal usage, in modal construction is done on set of samples having predetermined classes called the training set. During modal usage is used for classifying unknown samples, where the known label of test sample is compared with the classified result from the model. Accuracy rate is the percentage of test set samples that are correctly classified by the model.
On accounting the performance evaluation of classifiers acting in extremely imbalanced datasets environment, algorithms will be hardly pressed for to classify test samples as members of the minority class, because the scores are discriminate given by the classifier are often biased toward the majority class. Accuracy is clearly a poor measure of the performance of a classifier on imbalanced data. Usually there is still some separation in the probabilities between classes. In order to compare across all possible thresholds, try to quantify the strength of a classifier with a nonparametric measure. The ROC and P-R curves will allow us to find the strength of a classifier at each possible threshold.
There are a lot of classifiers commonly used in machine
learning, and classifiers perform differently with the exact same feature set. Thus, to measure the quality of a feature selection metric, it is not sufficient to simply select one classifier. So evaluate the feature set on different classifiers with different biases to truly measure the strength of a feature selection method. On previous research in feature selection for imbalanced data numerous different types of classifiers providing varying degree of performance have been used. According to the classification scores of the classifiers a confusion matrix is plotted as in table 2, and the classifier’s accuracy is calculated using formula given in (8).

TABLE 2

CONFUSION MATRIX

Class I having x samples, where x ≥ 1.

Class II having n-x samples, where x ≤ n-1 and 2x

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 5

ISSN 2229-5518

Accuracy =

(TP  TN)

(T P  TN + FP  FN)

(8)
Here we start with a set of data X = {(xi, ci)}, where each xi is a training sample and ci is set of associated samples for to be classified and the hyper-plane is written using equation wTx +

3.3 Non Parametric measure evaluation

The performance evaluation can be done by Receiver Operating Characteristics (ROC) and the P-R curve. We use the ROC [19] curve for to measure the overall goodness of a classifier across all possible discrimination thresholds between the two classes. Classifiers give not only a classification for a sample, but also a quantity representing how confident the algorithm is of these results. Using the confidence values for the samples, we can calculate statistics using the discrimination threshold between each pair of samples. The ROC calculates the true positive and false positive rates. The pairs of rates can then be plotted to form the ROC curve. Using the raw curves to choose the proper threshold for best classification is difficult, but we can use the curve to get one number that quantifies the strength of a classifier. The area under ROC curve is the evaluation statistics used to evaluate classifier.

4 CLASSIFICATION ALGORITHMS

The feature selection affects different classifiers, but linear
w0 = 0. The goal is to select the weight vector and bias that separate the data at maximum limit. If the two parallel hyper-
planes is having the maximum margin then it is expressed as wTx+w0 = ±1. This procedure is account for each sample of the classes in ci by seeing weather all wTxi + w0 ≥ 1.

4.2 Naïve Bayes Classifier

In Naïve Bayes classifier [8] instead of finding a single discriminant and using that as a classifier, we can suit a probability model using the features as conditions for the probability of a sample being drawn from a class. In a probability model, we would like to find p(C|F1, . . . , Fn), where each Fi is the value for each feature and C is the class of the sample. This is commonly called the posterior. Once we have the posterior for each class, we assign a sample to the class with the highest posterior. It is difficult, if not impossible, to find the posterior directly. However, if we use Bayes’ rule, we can express the posterior as a ratio of the prior times the likelihood over the evidence. Formally, this is expressed as given in (9).

p(C)p(F , . . . , F | C)

p(C | F , . . . , F ) =

SVM [1] is fairly resistant to feature selection and can show
improved results. On the other hand, feature selection has a

p(F1 , . . . , Fn )

(9)

stronger influence on the K-Nearest neighbor and Naïve Bayes classifiers. So the best feature selection metrics should be able to help a classifier perform better in despite of the inherent resistance.

4.1 Support Vector Machine

The SVM [20] is better suited to imbalanced data class problem since, only support vectors are considered in classification. It considers a subset of all data from both classes and the optimum hyper-plane is selected, at each of the iterations. The subsets can be formed such that there is no imbalance in the training. It has the simplest way to classify points into two classes. At first assume that the classes can be linearly separated from each other, by this assumption we can easily discriminate between the samples in each class without knowing anything about the distribution of training samples.
It uses a linear equation for discriminating while classifying. To learn about linear discriminating principle of the classifier, we only need to know about the parameters such as weight vector and the bias. One problem with learning linear discriminating principle is that there are many different weight vector and bias combinations that could correctly classify the training data. If each of these is correct, then we have to select any one of these discriminating threshold. In SVM, the best discriminating threshold is that it maximizes the distance from the separating hyper-plane formed by the discriminating the samples on both sides. If such a hyper-

4.3 Nearest Neighbor

The nearest neighbor algorithm [21] is an instance-based Lazy learning algorithm, which defer the computation for classifying a sample until a test sample is ready to be classified. It meets the criteria by storing the entire training set in memory and calculating the distance from a test sample to every training sample at classification time; the predicted class of the test sample is the class of the closest training sample.
The nearest neighbor algorithm is a specific instance of the
k-nearest neighbor algorithm where k = 1. In the k-nearest
neighbor algorithm, when we get a test sample we would like
to classify, we tabulate the classes for each of the k closest
training samples and predict the class of the test sample as the
mode of the training samples’ classes. The mode is the most

common element of a set. In binary classification tasks, k is normally chosen to be an odd number in order to avoid ties. Selecting the best value of k is difficult, and it is even more problematic when dealing with imbalanced data. The imbalance between the two classes makes it likely that more of the k nearest training samples will be found in the majority class as k increases. We used k <= 5 because this value is the most fair to the minority class. Nearest neighbor algorithms can use any metric to calculate the distance from a test sample to the training samples. A metric is a two-argument function d(x, y). The standard metric used in nearest neighbor algorithms is Euclidean distance which is given in (10).

n

plane is formed, it is called the optimal separating hyper-plane
d(X, Y) =

X i  Yi 

(10)
or the maximum-margin hyper-plane.

i1

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 6

ISSN 2229-5518

5 SIMULATION RESULTS

In this project the binary datasets are given as inputs and the feature selection metrics are acted on those dataset so that an constrained set of selected features were extracted out of all features and performance of the metrics were evaluated using AUC by learning those selected features on classifiers. This system has been developed and implemented in MATLAB tool and it is worked under Windows 7 OS with Core i3-370M Processor environment. We have accounted some of our results here.

5.1 Dataset Selection

The various small sample cancer datasets are downloaded from NCBI are used in the experiments. The data taken as input are various microarray binary class disease sample gene expression datasets. The details of those datasets are tabulated in table 3.

5.2 Feature Ranking

PCC, S2N, FAST and FAIR are four continuous feature selection metrics used to select the most expressive genes. In which each of the feature selection metrics is trained on leukemia binary class dataset with 7129 genes and 72 samples.

TABLE 3

DETAILS OF GENE EXPRESSION DATASET

ALL- Acute Lymphoblast Leukemia, AML- Acute Myeloid Leukemia, CGL- Germinal Centre B-Like, ACL- Activated B-Like, RA- Rheumatoid Arthritis, OA- Osteoarthritis. HC- Healthy Controls, DM2- Diabetes Mellitus 2, NGT-

Normal Glucose Tolerance, N-Normal, T- Tumor.

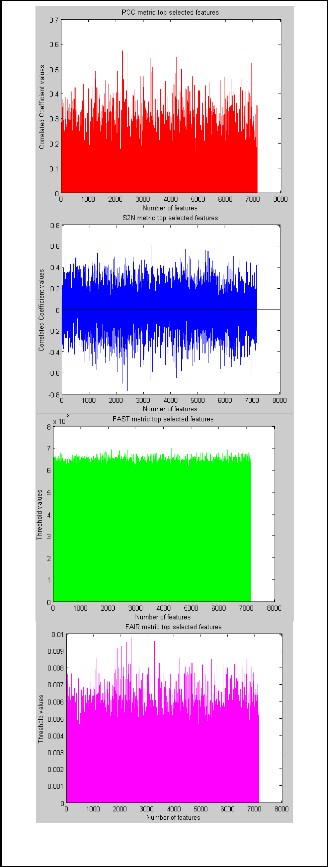
The metrics holding their coefficient values for each feature, with number of features on X-axis and correlated coefficient values on the Y-axis are taken for PCC and S2N respectively. For PCC and S2N ratios the features having maximum coefficient values are taken as top features. In FAST and FAIR metrics the threshold area values are taken for each of the features. Here by taking the number of features on X- axis the relative threshold area values are plotted on the Y-axis for both the metrics are shown in Fig. 2 respectively.

Fig. 2. Feature selection metrics showing correlated coefficient values for each feature PCC, S2N, FAST, FAIR.

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 7

ISSN 2229-5518

TABLE 4

MOST EXPRESSIVE GENES SELECTED BY PCC METRIC

of PCC, S2N metric and the threshold area values of FAST and FAIR metrics we assigned the rank to each of features. We have displayed the top 10 features along with Gene no, Gene ID, description and coefficient values in table 4 as same as the model used at [22].The top 10 features selected by higher areas in FAST metric are shown in table 5.

5.3 Classification Task Data Setup

The feature scores of the top 10 genes are separated in 50:50 ratio based on number of samples and the class of the samples.

TABLE 6

TEST AND TRAIN SAMPLES FOR LEUKEMIA DATA

Here, the first half is taken as training set and the next half is taken as test set as shown in table 6, the test data sets are eventually in process of forming a class imbalance ratio.

5.4 classification task assessment

The classifiers used for classification task is SVM, K-NN and Naïve Bayes techniques. While training and testing the Leukemia data’s top 10 feature score using SVM as classifier,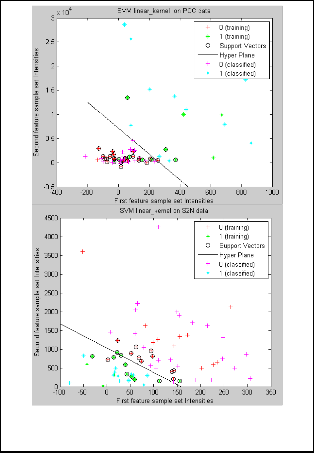

On selecting the top most expressive genes a classifier can induce higher accuracy scores, so we took top 10 features for various feature selection metrics in Leukemia data.

TABLE 5

MOST EXPRESSIVE GENES SELECTED BY FAST METRIC

We have obtained highly relative non redundant genes without over fitting. By seeing the correlated coefficient value

Fig. 3. SVM Classification for Feature Selected Data by PCC

and S2N metrics.

the results produced are shown in fig 3. In a feature space containing intensities of first feature to the intensities of next

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 8

ISSN 2229-5518

feature for the same sample set are plotted in X -axis and Y - axis respectively, during training support vectors and an optimized hyper-plane is created and classification of test samples are done based on the predicted support vectors on either side of hyper-plane as positive and negative. We also quantified the classification task using non parametric measure ROC as to know the class imbalance effect during classification process.
The accuracy produced by various classifiers is found by comparing the actual class with the predicted class of test samples and are shown in table 7.

TABLE 7

TEST AND TRAIN SAMPLES FOR LEUKEMIA DATA

5.5 Performance comparison between various disease datasets

We operated the various datasets on various feature selection metrics to the classifier approaches and found the best suited metrics-classifier approach for the disease sample.

TABLE 8

PERFORMANCE COMPARISON OF VARIOUS APPROACHES

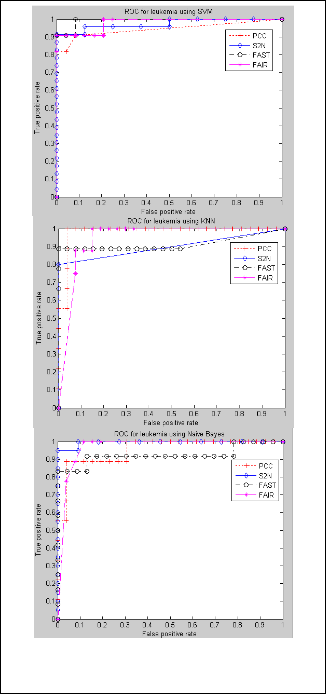
Fig. 4 . ROC Curve Showing Feature Selection Metrics Performance in SVM, KNN and Naïve Bayes Classifiers on Leukemia Dataset

The ROC graph plotted for the feature selection metrics is illustrated on fig 4. Here, FPR is taken along X-axis and TPR along Y-axis.
We also compared our results on classification with the other approaches’ results are shown as tabulation 8.

IJSER © 2012

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 3, June-2012 9

ISSN 2229-5518

5 CONCLUSION

Thus the goal is to show the effectiveness of various methodologies of suppressing class imbalance on any classifiers is evaluated using AUC statistics for the various feature section metrics. The evaluation technique makes users for to select suitable metrics while learning suitable genomic datasets while lowering the ratio of Imbalance classes. Also highly optimized features are selected by verifying over-fitting and redundant occurring problems in samples.

REFERENCES

P. Ganesh Kumar is currently working as an Assistant Professor in the Department of Information Technology, Anna University of Technology, Coimbatore. From July 2003 to August 2008, he worked as a Lecturer in the Department of Information Technology, Kalasalingam

University, Krishnankoil. He received his BTech degree in Information Technology from the University of Madras in May 2003, MS (By Research) degree in Information Technology from Anna University Chennai in September 2008 and he received his PhD degree from the Anna University of Technology, Coimbatore in March 2012. He has published 8 international journals and 22 international conferences. His research interest is application of soft computing techniques in data mining, and bioinformatics.

J. Briso Becky Bell is currently doing M.Tech Information Technology in the Department of Information Technology in Anna University of Technology, Coimbatore. He received his B.Tech degree in Information Technology, under Anna University Chennai in May 2010.

His research interests are data mining and bioinformatics.

IJSER © 2012

http://www.ijser.org