Ms.S.Sumathi is currently pursuing masters degree program in Embedded Systems Technologies in Anna University of Technology-Tirunelveli, India. E-mail:kanch2386@gmail.comThe research paper published by IJSER journal is about Tight focusing of circularly polarized light beam for the fabrication of NEMS 1
ISSN 2229-5518
Tight focusing of circularly polarized light beam for the fabrication of NEMS
S.Sumathi, K.Gokulakrishnan, K.B.Rajesh
1 INTRODUCTION
Focused femtosecond laser vortex pulses are routinely used to micromachine or change the properties of different materials.By focusing the pulses very tightly and by simultaneously keeping the light intensity in the focal region near the optical breakdown threshold the structural changes can be spatially localized to 10’s of nanometers[1].So far,this combined approach has been used in high density optical recording [2],fabrication of 3-D nano fluidic channels [3],single cell surgery [4],and synthesis of novel material phases using linearly polarized Laugerre Gaussian (LG) beams.
In this paper,we investigate the vectorial nature of tightly focused femtosecond laser vortex pulses.Specifically,we demonstrate that the circularly polarized vortex pulses of the opposite handedness,but with an identical intensity distribution at the entrance pupil of the focusing optics can produce ablation features which dramatically change in shape and size.
2 THEORY
In our experiment, we ablate Silicon in air either by using fixed spot radiation or by moving the sample perpendicular to the laser beam propagation Z.The ablation is performed on the basis of spin and orbital angular momentum of the pulses,which are defined by the handedness of circular polarization σ and the sign of m respectively were either parallel or anti-parallel.According to the theory [15],these two situations correspond to quite different focal intensity distributions in the regime of tight focusing.
————————————————
Mr.K.Gokulakrishnan is currently working as an Assistant Professor in
Anna University of Technology-Tirunelveli, India. E-mail:gk39762@gmail.com
Mr.K.B.rajesh is currently working as an Assistant Professor in
government arts college,Dharmapuri,India.E-mail:rajeshkb@gmail.com
A schematic diagram of the suggested method is shown in Fig-1.The analysis was performed on the basis of Richards and Wolf’s vectorial diffraction method widely used for high NA focusing systems at arbitrary incident polarization. The complex amplitudes of the longitudinal(Ez) and transverse electric field components( Ep) can be written as
+ 
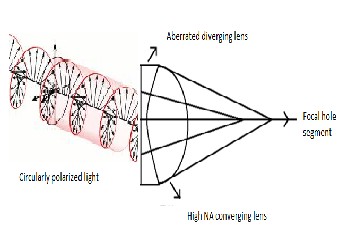
Figure 1:Focusing of circularly polarized light using lens axicon
For the left handed circularly(σ=1) polarized Laguerre
Gaussian beam and as:
} (3)
For the right handed circularly(σ=-1) polarized Laguerre
Gaussian beam,where:
(5)
IJSER © 2012
The research paper published by IJSER journal is about Tight focusing of circularly polarized light beam for the fabrication of NEMS 2
ISSN 2229-5518
are the unit vectors in the circular basis.
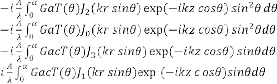
(9)
(6) (7) (8)
We observed that the increase in the NA results in the decrease of the DOF.The proposed high NA lens axicon system generates sub wavelength super long dark channel without any annular truncation.
Fig-2 Intensity distribution of the focused field near focus for the
a= (10)
b=1+cosθ (11)
c=1-cosθ, (12)
G= γ
(13)
Where G is the function of the incident beam, 
is the amplitude at the peak of intensity,A is the coefficient that depends upon the optical parameters of the system, k
is the wave number of light in vacuum,r is the radial distance from the z-axis,
and 
are the angular coordinates of r, 
is the Bessel function of the first kind of order n, the truncation parameter γ= is the ratio of the entrance pupil aperture
radius R and the beam size parameter ω, and α=arcsin(NA).In our experiments, α=1.12,R=2mm and ω=1.8mm.The integrals were calculated only for the central wa
velength of the femtosecond laser radiation which has a
FWHM spectral bandwidth of ~5nm.This approximation is valid as the influence of light polychromaticity on the
intrafocal intensity distribution becomes noticeable only for very short (˂10fs) broadband laser pulses.
3 RESULTS
We perform the integration of Eq. (1) numerically using parameters λ =1, NA=0.6 and β=1.2 as in [9].For simplicity, we assume that the refractive index n = 1 and A = 1.
The intensity distribution of the lens axicon is evaluated by by the function T(θ), where T(θ) is the non-paraxial
transmittance function of the thin aberrated diverging lens.
(14)
Where 
is the aberration coefficient. In our calculation,we take f=18.4mm and
circularly polarized beam focused by high NA lens axicon. The other parameters are β=2 and NA =0.9 (a,d)Intensity distribution produced by the transverse components of right and left circularly polarized light.(b,e)Intensity distribution produced by longitudinal component right and left circularly polarized light.(c,f)Total intensity distribution of right and left circularly polarized light
Since such a long uniform sub wavelength focal hole segment is generated without any annular aperture, the intensity of the focal hole segment also remains very high.
4 CONCLUSION
The intensity distributions of circularly polarized beam that has a double-ring-shaped transverse mode pattern tightly focused by high NA lens axicon were calculated based on vector diffraction theory. It is observed that the distribution of the electric field near the focus varied drastically with the degree of truncation of the incident beam by a pupil. This effect offers an additional degree of freedom to control the shape and size of laser-machined structures on a sub-wavelength scale.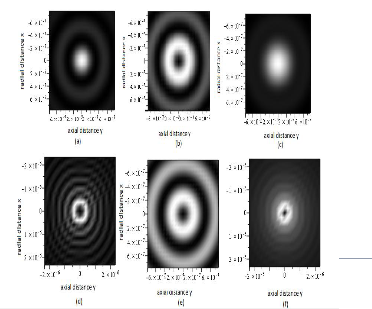
REFERENCES:
2012
.ijser.org
The research paper published by IJSER journal is about Tight focusing of circularly polarized light beam for the fabrication of NEMS 3
ISSN 2229-5518
[5]. N.Shen,D.Datta,Ch.B.Schaffer,Ph.LeDue,D.E.Ingber,E.M azur, “Polarization-dependent ablation of silicon using tightly focused femtosecond laser vortex pulses”MCB
2,17(2005)
[6]. A.Vailionis,E.G.Gamaly,V.Mizeikis,W.Yang,A.V.Rode and S.Juodkazis. Nature commun. “Polarization- dependent ablation of silicon using tightly focused femtosecond laser vortex pulses” Optics Letters, Vol. 37, Issue 2, pp. 226-228 (2012)
[7]. M.Gu,”Advanced Optical Imaging Theory”
(Springer,Heidelberg,2000)
[8]. R.Dorn,S.Quabis and G.Leuchs. “High-numerical- aperture focusing of radially polarized doughnut beams with a parabolic mirror and a flat diffractive lens”
Phys. Rev.Lett. 91,233901(2003)
[9]. L.Novotny, M.R.Beversluis, K.S.Young worth and
T.G.Brown .Phys. Rev. Lett.86, 5251(2001)
[10] N.Hayazawa, Y.Saito and S.Kawata.” Confinement of enhanced field investigated by tip-sample gap regulation in tapping-mode tip-enhanced Raman microscopy”Appl. Phys. Lett.85,6239(2004)
[11]
.
[12]
.
[13]
.
[14]
.
[15]
.
D.P.Bliss and T.G.Brown. “Stress birefringent, space- variant wave plates for vortex illumination” Opt Lett.28,
923 (2003)
M.Padgett and R.Bowman. “Twisted light for micromanipulation and beyond”Nature Phot.. 5,343 (2011)
B.Jia, H.Kang, J.Li and Min Gu. “Conditions for tighter focusing and higher focal depth of radially polarized vector beam” opt let.34, 1918 (2009)
C. Hnatovsky, V.G. Shve dov, W.Kroliow ski, A.Rode.” Materials processing with a tightly focused femtosecond laser vortex pulse” Opt.Lett. 35, 3417 (2010). C.Hnatovsky,V.Shvedov, W.Krolikowski and A.Rode. “Focusing properties of vector vortex beams emitted by photonic-crystal lasers”Phys Rev Lett 106,123901(2011)
[16] P.Torok and P.R.T Munro.” Rigorous analysis of spheres in Gauss-Laguerre beams”Opt.Exp. 12, 3605 (2004)
[17] K.M.Romallosa, J.Bantang nd Caeser Saloma. “Three- dimensional light distribution near the focus of a tightly- focused beam of few-cycle optical pulses” Phys. Rev.A
68,033812(2003)
[18] J.Bonse,S.Baudach,J.Kruger,W.Kautek,M.Lenzner. “Femtosecond and nanosecond laser fabricated substrate for surface-enhanced Raman scattering” Appl.Phys.A74,19(2002)
IJSER © 2012