---------------------------------------------
International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 1
ISSN 2229-5518
Thermoelastic Problem of a Hollow Elliptical Cylinder Subjected to a Partially Distributed Heat Supply
S. D. Bagde and N. W. Khobragade
Abstract- This paper presents the theoretical treatment of a thermoelastic problem of a hollow elliptical cylinder due to par- tially distributed heat supply on the outer curved surface. Integral transform techniques have been utilized to obtain the so- lution having the influence of heating and cooling conditions for the problem in the form of a Mathieu series.
Key Words- Temperature distribution, thermal stress, integral transform .
Ams Subject Clasification No: 74G70, 74E05, 74A10 .
————————— ——————————
This paper presents the theoretical treatment of a thermoelastic problem of a hollow elliptical cylinder due to partially distributed heat supply on the outer curved surface.
2. STATEMENT OF THE PROBLEM
We consider elliptical cylinder of inside radius a, outside radius
b (where a < b) and thickness . The geometry of the cylinder
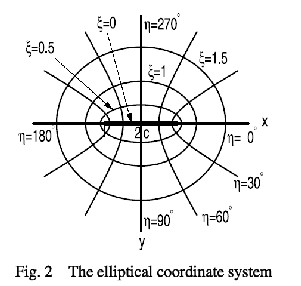
The curves constant represent a family of confocal hyperbolas while the curves constant represent a family of confocal ellip- ses. The length 2c is the distance between their common foci (refer to Figure 1). Both sets of curves intersect each other orthogonally at
every point in space. The parameter varies from 0 where it de-
fines the interfocal line, to 0 , the coordinate is an angular co-
indicates that an elliptic coordinate system ( ,, z) is the most
appropriate choices of reference frame, which are related to the
ordinate taking the range [0, 2 ) , and
z (0, ) . It is noted
rectangular coordinate system (x, y, z) by the relation
that c is denoted as
2c (a2 b2 )1/ 2
and 0
tanh1 (b / a) in
x c cosh cos,
y c sinh sin,
z z
terms of the semi major axial-length a and the semi minor axial-
length b. The heat conduction differential equation is given as
(1)
2 2 2
h2 T T T 2h0 (T T ) 0
(2)
---------------------------------------------![]()
![]()
![]()
2
where
2
z 2 a
Sunil D. Bagde, research scholar in the P.G
Department of Maths, RTM Nagpur University Nagpur,
INDIA
h 2
c 2
(cosh cos 2) / 2
(3)
(E-mail: sunilkumarbagde@rediffmaill.com ).
N. W. Khobragade, Professor in the P.G Department of
Maths,RTM Nagpur University Nagpur, INDIA
Introducing the following dimensionless parameters
IJSER © 2012
International Journal of Scientific & Engineering Research Volume 3, Issue 10, October -2012 2
ISSN 2229-5518
![]()
![]()
h 2 h2a2 , h
h a
![]()
![]()
![]()
![]()
![]()
![]()
![]()
, , b a
![]()
0 0
0
13)
![]()
![]()
![]()
T ( ,, z) T ( ,, z)
T0
![]()
![]()
2 ij
ij
![]()
E rTk
(i, j , )
M ( , 0,1, 0) 0 ,
M ( , 0,1, L) 0 , for all
1 R , 0
E rTk ao
(4)
(14)
Thus, the equations (1) to (14) constitute the mathematical for- mulation for heating and cooling problems under considera-
The equation (2) can be written in the dimensionless form as:
tion.![]()
2
![]()
![]()
2 2 2
![]()
![]()
h 2 T T T 4h0
(T T
) 0
(5)
![]()
![]()
![]()
1 2
where
2
z 2 2 a
The dimensionless radial and tangential stresses are given as [3]![]()
h 2 (cosh 2 cos 2) / 2
(6)
![]()
![]()
h 2 ![]()
![]()
e h
![]()
![]()
sinh(2 ) e h![]()
sin(2 )
(15)
![]()
rr
and compiling various dimensionless boundary conditions are de-
![]()
2 2![]()
![]()
![]()
2
fined to determine the influence of the thermal boundary condi- tions on the thermal stresses as:
![]()
![]()
h
![]()
2 ![]()
2![]()
e2h 4
![]()
2![]()
![]()
sinh(2 )
![]()
e2h 4
![]()
2![]()
![]()
sin(2 )
(16)
M (T , 0,1,i ) R1(, z) , for all
h z h
![]()
![]()
h 2
![]()
![]()
2 ![]()
e2h 4
![]()
![]()
sinh(2 ) e h![]()
sinh(2 )
(17)
M (T , 0,1,0 ) R2 (, z) , for all
h z h
(7)
![]()
2![]()
![]()
![]()
2
(8) where k1 and k2 are the radiation constants on the two annular fin surfaces
M z (T , 0,1, h) Z1( ,) , for all i o
(9)
Determination of the heat conduction equation: Applying integral transformation defined in [1] to the equations (5), (7), (8) over the variable z with responds to the boundary
condition (9-10) one obtains
M z (T , 0,1, h) (Q0 / ) Z2 ( ,) , for all i o
![]()
![]()
2 2
h2 T T 2h0 (T T
) 0
(18)
(10)
![]()
![]()
2
2 a
On the other hand for the cooling process the temperature distribution
T ( ,, z) satisfies the equation![]()
M (T , 0,1,i ) R1(, z)![]()
M (T , 0,1,0 ) R2 (, z)
(19)
(20)![]()
2
![]()
![]()
![]()
2 2 2
![]()
![]()
h 2 T T T 4h0
(T T
) 0
(11)
Where T denotes the transformed function of T , an are the![]()
![]()
![]()
1 2
2
z 2 2 a
eigenvalues of the transcendental equations
and the various dimensionless boundary conditions are
M ( ,1, 0, 0) M ( ,1, 0, t0 ) , for all
1 R , 0 L
1a cos(ah) 1 sin(ah)2 cos(ah) 2a sin(ah)
(12)
IJSER © 2012
International Journal of Scientific & Engineering Research Volume 3, Issue 10, October -2012 3
ISSN 2229-5518
2a cos(ah) 2 sin(ah)1 cos(ah) 1a sin(ah)
(21)![]()
![]()
1 k1 , 1 1 , 2 k2 , 2 1 responds to the boundaries con- ditions of type (12.2.8) as
M z (T , 1, 1, h) 0 , M z (T , 2 , 2 , h) 0
and
(22)
f (n, t)
h
f ( z, t)Pn ( z) dz
h
(23)
Here the kernel is given by the orthogonal functions in the in-
terval h z h as
Pn (z) Qn cos(an z) Wn sin(an z)
where
Qn an (1 2 ) cos(anh) (1 2 ) sin(anh)
Wn (1 2 ) cos(anh) (2 1)an sin(anh)
(24)
In this paper presents the theoretical treatment of a thermoelas- tic problem of a hollow elliptical cylinder due to partially dis- tributed heat supply on the outer curved surface.
The authors are thankful to University Grant Commission, New Delhi for providing the partial financial support under Rajiv Gandhi National Fellowship Scheme.
functions, 1st ed., Oxford University Press (1947).
IJSER © 2012