equalization
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 638
ISSN 2229-5518
The Comparative Study of Adaptive Channel Equalizer Based on Feed Forward Back Propagation, Radial Basis Function Neural Network(RBFNNs) & Least Mean Square (LMS) Algorithm
Darshna Kundu(M. Tech Scholar)* M.K.Jain(Associate Professor)**
Artificial neural networks (ANNs) takes their name from the network of nerve cells in the brain.Recently,ANNs has been found to be an important technique for classification and optimization problem. Neural networks (NNs) have been extensively used in many signal processing applications. Linear & Nonlinear adaptive filters based on a variety of neural network models have been used successfully for system identification in a wide class of application. NNs have been most popularly applied to channel equalization of digital communication channels, in particular, due to their capacity to form complex decision regions. The mean square error(MSE) criterion, which is usually adopted in neural learning is of interest in the channel
equalization
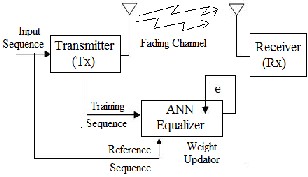
Fig: (1) A Block Diagram of Digital Communication System using Artificial
Neural Network based Equalizer [2].
ANNs are non–linear data driven &follows self adaptive approach as opposed to traditional model based methods.They are powerful tools for modelling,specially when the underlying data relationship is unknown.ANNs can identify and learn correlated patterns between input data sets
and corresponding target values. ANNs can be used to predict
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 639
ISSN 2229-5518
the outcome of new independent input data after training ANNs imitate the learning process of human brain & can process problems involving non-linear & complex data even if the data are imprecise & noisy.
A very important feature of these networks is their adaptive nature,where “learning by example”replaces “programming” in solving problems this feature makes such computational model very appealing in application domain where one has little or incomlete understanding of the problem to be solved but where training data readily available. ANN is capable of performing nonlinear mapping between the input and output space due to its large parallel interconnection between different layers and the nonlinear processing characteristcs. Thus they are ideally suited for the equalization of AWGN communication channel which are noisy as well as non-linear.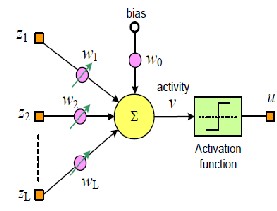
Fig:(2) Structure of a single Neuron
The terminology of ANNs has been developed from a biological model of the brain.A neural network consists of a set of connected cells :The neurons . The neurons receives input either from input cells or other neurons and performd some kind of transformation of the input & transmit the out come to other neurons or to output cells . The neural networks are built from layers of neurons connected so that one layer receives input from the preceeding layer of neurons and
passes the output on the subsequent layers.
Each neuron is associated with three parameters whose learning can be adjusted;these are the connecting weights,the bias and the slope of nonlinear function.A feed forward structure with input,output,hidden layers and nonlinear
sigmoid functions are used in this type of network.
The basic structure of an artificial neuron is presented in Fig.2.The operation in a neuron involves the computation of the weighted sum of the inputs and threhold.The resultant signal is then passed through a nonlinear activation function.This is also called a perceptron,which is built around a non linear neuron.![]()
The output of the neuron may be represented as,
………(1)[15]
Where α(n) is the thershold/bias to the neurons at the first layer, wj (n) is the weight associated with the jth inputs to the neuron and φ(.) is the nonlinear activation function. Different types of nonlinear activation functions are shown in fig(5).
The commonest type of ANN consists of three groups, or layers, of units: a layer of "input" units is connected to a layer of "hidden" units, which is connected to a layer of "output" units(Fig.3).The activity of the input units represents the raw information that is fed into the network. The activity of each hidden unit is determined by the activities of the input units and the weights on the connections between the input and the hidden units. The behavior of the output units depends on the activity of the hidden units and the weights between the hidden and output units.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 640
ISSN 2229-5518
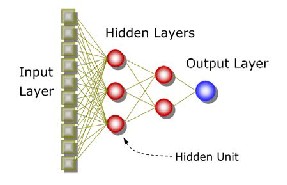
Fig:(3) A simplified multilayer feed forward neural network
Radial Basis Function Networks (RBFN) consists of 3 layers; an input layer, a hidden layer & an output layer. The hidden units provide a set of functions that constitute an arbitrary basis for the input patterns. Hidden units are known as radial centers and represented by the vectors c1, c2, c3……….. ch. Transformation from input space to hidden unit space is nonlinear whereas transformation from hidden unit space to output space is linear. Dimension of each center for a p input network is [p*1].
Different types of radial basis functions could be used, but the
most common is the Gaussian function: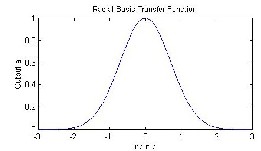
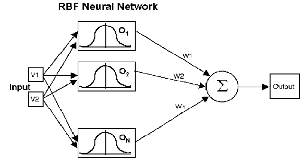
Fig:(4) Architecture of Radial Basis Function network
The behaviour of an ANN depends on both the weights and the input-output function (transfer function) that is specified for the units. This function typically falls into one of three categories: linear (or ramp), threshold, sigmoid. For linear units, the output activity is proportional to the total weighted output.
-For threshold units[Fig.5(b)], the output are set at one of two levels, depending on whether the total input is greater than or less than some threshold value.
This function can be written like as![]()
………..(2)[15]
-For sigmoid units[Fig.5(c)], the output varies continuously but not linearly as the input changes. Sigmoid units bear a greater resemblance to real neurons than do linear or threshold units, but all three must be considered with rough approximations.
This function is s-shaped, is the most common form of the activation function used in artificial neural network. It is a function that exhibits a graceful balance between linear & nonlinear behavior. It is represented as:![]()
……….(3)[15] Where ![]()
is the input to the sigmoid function and ‘a’ is the slope of the sigmoid function. For the steady convergence, a proper choice of ‘a’ is required.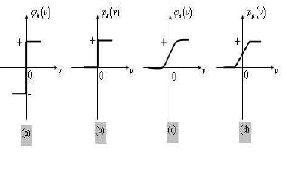
Fig:(5) Different type of non linear activation/transfer function[15]
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 641
ISSN 2229-5518
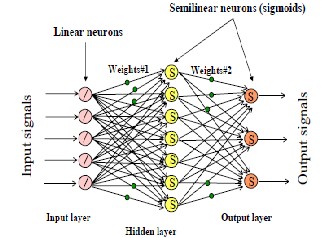
Fig:(6) A structure of multilayer perceptron
In the multilayer neural network or multilayer perceptron (MLP), the input signal propagates through the network in a forward direction,on a layer-by-layer basis.This network has been applied successfully to solve some difficult and diverse problemsby training in a supervised manner with a highly popular algorithm known as the error back-propagation algorithm.
The scheme of MLP using four layers is shown in below fig.6 represents the input to the network, fj and f k represent the output of the two hidden layers and yl (n) represents the output of the final layer of the neural network.The connecting weights between the input to the first hidden layer,first to second hidden layer and the second hidden layer to the
output layers are represented w ij, , wjk and w kl, by respeatively.![]()
If P1 is the number of neurons in the first layer,each element of the output vector may be calculated as,
………..(4)[15]
where αj is the threshold to the neurons at the first layer.N is the number of inputs and φj is the non linear activation function.The time index n has been dropped to make the equations simpler.Let P2 be the number of neurons in the second layer. The output of this layer is represented as, f k and may be written as![]()
……….(5)[15]![]()
Where, ![]() is the thershold to the neurons in the second layer.The output of the final layer can be calculated as
is the thershold to the neurons in the second layer.The output of the final layer can be calculated as
………..(6)[15]
Where,αl the thershold to the neuron at the final layer and P3 is the number of neurons in the output layer. The output of the MLP may be expressed as![]()
………….(7)[15]
In BP algorithm, initially the weights and thresholds are initialized as very small random values.The intermediate and the final outputs of the MLP are calculated by using (4),(5) and (6).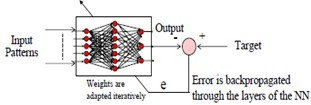
Fig:(7) A basic block diagram of feed forward neural nework equalizer training using back propagation algorithm
The final output yl (n) at the output of neuron 1,is compared with the desired output d(n) and the resulting error signal el (n) is obtained as
e l (n) = d(n) − y l (n)………(8)![]()
The instantaneous value of the total error energy is obtained by summing all error signals over all neurons in the output layer,that is
………..(9)[15]
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 642
ISSN 2229-5518
where P3 is the number of neurons in the output layer
This error signal is used to update the weights and thresholds of the hidden layers as well as the output layer. For measuring degree of matching ,MSE(mean square error) performance criteria is taken into consideration
The updated weights are,![]()
………..(10)[15]![]()
…………(11)[15]![]()
…………(12)[15]
Where,![]() wkl (n),,
wkl (n),, ![]() wjk (n), and
wjk (n), and ![]() wij (n),are the change in weights of the output, hidden and input layer respectively.
wij (n),are the change in weights of the output, hidden and input layer respectively.
The thresholds of each layer can be updated in a similar manner,that is![]()
……….(13)[15]![]()
………..(14)[15]![]()
……….. (15)[15]
Step 1: obtain a set of training data
Step 2: set up neural network model
[Number of input neurons, Hidden neurons, and
Output neurons, number of layers]
Step 3: Set learning rate η and momentum rate α
Step 4: initialize all connection weights wij , wjk, w kl and bias
values αj , αk ,αl
Step 5: set minimum error, Emin
Step 6: start training by applying input data and propagate through the layers then calculate total error.
Step 7: Back propagate error through output & hidden layer and adapt weights.
Step 8: Back propagate error through input & hidden layer and adapt weights.
Step 9: check it error is ![]() Emin
Emin
If not ….repeat step 6-9,if yes….stop training.
2.2.2 LMS(standard LMS) algorithm:-
The least-mean square (LMS) algorithm updates the linear filter coefficients such that the mean square error (MSE) cost function is minimized
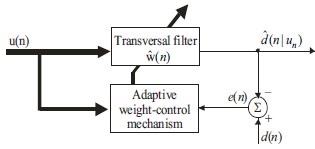
Fig:(9) Basic Block diagram of Adaptive Channel Equalizer Based on gradient decent algorithms [17]
LMS perform the following operation to update coefficients of the adaptive filter.
u (n)= Input signal
h (n) = system response e (n) = Error signal![]()
d (n)= desired signal. (n)=Transversal FIR filter output
![]() = weight vector of Transversal FIR filter ξ (n) = E [e (n)] ………………………(16)[4] The error estimation e (n) is
= weight vector of Transversal FIR filter ξ (n) = E [e (n)] ………………………(16)[4] The error estimation e (n) is
![]()
e (n) = d(n) – ![]() (n) …………………….(17)[4] (n)=w (n)*u (n) …………………..(18)[4]
(n) …………………….(17)[4] (n)=w (n)*u (n) …………………..(18)[4]
Calculates the error signal e(n) by using the equation(2). Coefficient updating equation is
w (n+1) = w(n) + µ u(n) e(n), …….(19)[4]
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 643
ISSN 2229-5518
Where µ is the step size of the adaptive filter (n) is weight vector and u(n) is the input signal vector.
Designing ANN models follows a number of systemic
procedures. In general, there are five
basics steps: (1) collecting data, (2) preprocessing data, (3)
building the network, (4) train,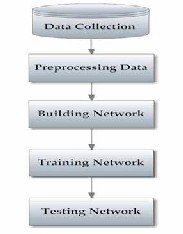
and (5) test performance of model as shown in fig(10)
Fig. 10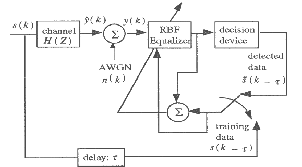
Fig:(11) A Block diagram of Radia Basis Function Neural Network Equalizer[18]
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 644
ISSN 2229-5518
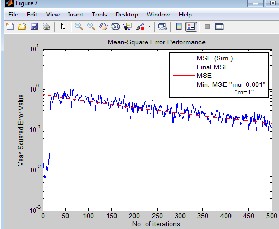
During simulation mean squared error (MSE) was used as performance criteria.This section presents the MSE performance of equalizer based on LMS for variety of parameters and neural network equalizer using back propagation algorithm to make a comparative analysis in terms of MSE performance criteria.The MSE versus Number of Iterations for AWGN Channel with Eb/No=1dB using QAM as modulation technique at reciever i/p was plotted for the performance analysis.
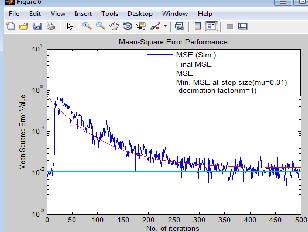
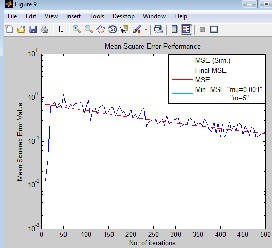
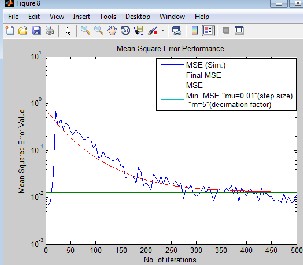
Fig(12) LMS based Equalizer for different values of step size(µ), & decimation factor(m).
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 645
ISSN 2229-5518
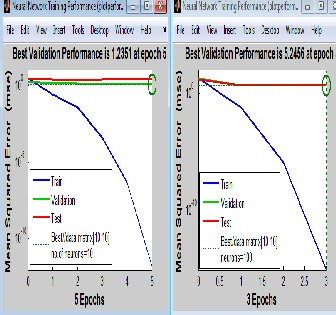
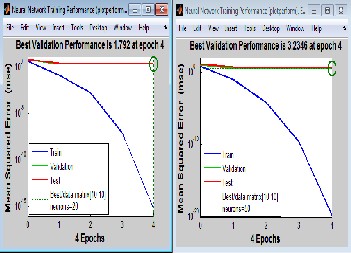
Fig.13 A MSE versus Number of Iterations (Epoches) curve for i/p & target data size [10 10],for different values of “hidden neurons”
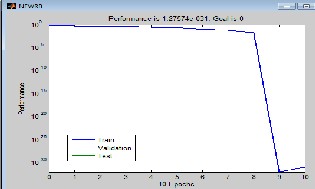
Fig. 14. A performance plot using “Radial Basis Function” as network type.
TABLE:1 Parameters and specification of the system
Data set size | [10 10] |
SNR range | 0-10 dB |
Channel type | AWGN |
Modulation type | QAM(quadrature amplitude modulation) |
TABLE 2. ANN parameters used for training
ANN Type | Feed forward, Radial basis function |
Number of layers | One input, one hidden, one output layer |
Input layer | Equal to transmitted data sequence |
SNR consideration | 1 dB |
Transfer function used | Tan-sigmoid, purelin |
MSE minimization limit | -inf |
Training type | LM-Back propagation |
In the above section, computer simulations are carried out & plots are drawn between MSE & number of iterations for performance analysis. Here each learning curve is the result of ensemble averaging the instantaneous squared error “e2(t)” [MSE] versus “number of iterations” .
In simulation of LMS based equalizer(fig.12) the results confirm that the rate of convergence of the adaptive equalizer based on LMS is highly dependent on the step-size parameter
µ.For a large step-size parameter (µ=0.01), the equalizer
converged to steady-state conditions in approximately 250 iterations(convergence faster). On the other hand, when µ was small (=0.001), the rate of convergence slowed down to 500 iterations. The result also shows that the mean square error
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 646
ISSN 2229-5518
(MSE) has lower value of 10-2 at µ=0.01(larger step size) than
MSE of 10-0.5 at µ=0.001(smaller step size).
Simulation results (Fig.13) relating to equalizer using feed forward two layer neural network presents a plot of MSE versus number of epochs(number of iterations), for data size [10 10], with different number of hidden neurons i.e.10,20,50&100.
In the plot of 10 hidden neurons by training a neural network, we got MSE of 10-12 within 5 epochs, in a plot of 20 neurons we got MSE value 10-15 in 4 epochs, & in a simulation of model with 50 hidden neurons MSE value achieved is 10-20 by taking
4 epochs only, and with 100 hidden neurons we got MSE 10-
16(approx.) in 3 epochs. From the study of simulations, it can be noticed that with the increase of number of hidden neurons (doubled) there is no very far reduction in MSE value, but computational complexity alongwith computation time increases upto a large extent..
Fig.14 depicts performance in terms of MSE versus number of iterations (epochs) of the equalizer based on ANN using RBF. It can be seen that we got MSE 10-32(approx.) in 3 epochs only.
Adaptive equalizer based on Artificial neural network employing network configuration such as Radial Basis function & feed forward using back propagation algorithm for different values of parameters such as data size, number of hidden neurons are simulated. In parallel to this gradient based LMS equalizer is also simulated & plots are obtained for different values of step size & decimation factor. On comparative analysis, we infer that a neural network model, as simulated above, yields a far reduction in mean squared error MSE with reduced convergence time compared to LMS based equalizer.
[1]. Jagdish C. Patra,Parmod K. Meher “Nonlinear channel equalization for wireless communication systems using Legendre neural networks”signal processing (11),2251-2262,Elsevier-2009.
[2]. Bidyut Bikash Baruah & Kandarpa Kumar Sarma
“ANN Bsed Equalization using coded inputs in
Nakagami-m Faded Channel” International Journal of Smart Sensors and Ad Hoc Networks (IJSSAN) ISSN Number 2248-9738 Volume-1, Issue-3, 2012
[3]. Ekta gurnani, Sheena Gupta “Decision Feedback
Equalizer” Using Artificial Neural Networks”
UACEE International Journal of Advances in Computer
Networks and its Security - Volume 2: Issue 1[ISSN 2250
- 3757]
[4]. Monson H. Hayes “Statistical Digital Signal Processing and Modeling” Wiley-India Edition
[5]. TheodoreS.Rappaport “Wireless Communications”
PHI-Second edition
[6]. Havkin.S. “Adaptive Filter Theory” Third Ed., Upper
Saddle Riven, N.J., Prentice-Hall.1996
[7]. Chanpreet Kaur, Rajesh Mishra “An FPGA implementation efficient equalizer for ISI removal in wireless application” 978-1-4244-9005-9/10/$26.00 -
2010 IEEE paper
[8]. IEEE Signal processing magazine, July, 2008
[9]. O.Macchi “Adaptive processing, the least mean squares approach with applications in transmission” West Sussex. England: John Wiley and Sons, 1995
[10]. Boroujeny,B.“Adaptive Filters: Theory and
Applications”1998
[11].SandhyaYogi,Prof.K.R. Subhashini,Prof. J.K.Satapathy “A PSO Based Functional Link Artificial Neural Network training algorithm for Equalization of Digital Communication Channels” 2010 5th International Conference on Industrial and Information Systems, ICIIS 2010, Jul 29-Aug 01,2010, India [12].Harmandeep Singh,S.S. Gill “Approaches to Channel Equalization” 2012 Second International Conference on Advanced Computing & Communication Technologies
[13].“Adaptive Equalization Algorithms: An overview”
International journal of advanced computer science and applications,Vol-2, Number-3,March 2011.
[14].Proakis, J.2001 “Digital Communication, Mc Graw- Hill,NY,4th edition
[15].Debidutta Mohanty “Channel equalization using GA
family”National Institute of technology Rourkela(orissa),2008 [16]. “Recursive Least Squares Adaptive Filters a better ISI Compensator” Sharma, O., Janyani, V and Sancheti, S. 2009
International Journal of Electronics, Circuits and Systems
[17]. ” M.F.Mosleh,A.H.ALNakkash “Combination of LMS and RLS Adaptive Equalizer for Selective Fading Channel European Journal of Scientific Research ISSN 1450-216X Vol.43
Number1(2010),pp.127-137
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 647
ISSN 2229-5518
[18]. M.S.Chavan, R.H.Chile “Optimizing the Performance of FuzzyImplemented Radial Basis Function Channel Equalizer with Subset Centre Selection” International journal of emerging trends technology in computer science Volume 1 Issue 1, May-June
2012 ISSN 2278-6856
[19]. Maitha H. Al Shamisi, Ali H. Assi and Hassan A. N. Hejase“Using MATLAB to Develop Artificial Neural Network Models for Predicting Global Solar Radiation in Al Ain” City – UAE United Arab Emirates University United Arab Emirates
*Darshna Kundu is currently pursuing M.Tech from
Lingayas University,Faridabad,Haryana,India.
Email : darshanakundu@gmail.com
**M.K.Jain is an Associate Professor currently working with Lingayas University,Faridabad,Haryana,India.
Email : mkjain@lingayasuniversity.edu.in
IJSER © 2013 http://www.ijser.org