
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 1

ISSN 2229-5518
Mwizerwa Pierre Celestin
—————————— ——————————
Abstract -This paper aims to respond to different mysteries which appear in news and blogs around the world about hypersonic flights, Colombia disaster, and hypersonic tests which are going on nowadays. People are really confused and wonder if, when we travel at hypersonic speed, the laws of physics change or if they remain intact. The laws of physics never change. It is we, humans, who have to respect those laws. In this paper, I will try to demonstrate and do all necessary calculations so people may find what is going on.
Index terms - Mach 20 speed, speed limit in atmosphere, terminal velocity, Colombia disaster, Falcon HTV-1 and 2 problem, hypersonic flights problems, hypersonic speed design proposals
After seeing a lot of hypersonic flights failures, I took my time and did some research about it. A big amount of money has been lost and many human lives have been lost as well. That’s why I took a paper and a pen to write about it. In fact, we cannot fly in atmosphere as we want, there are the resistance forces which oppose to movement and prevent us to move as quickly as we want. As those forces are directly proportional to the speed square, they grow very quickly and become extremely big so that they block the object travelling in the atmosphere. This is the case for example, of Colombia, Falcon HTV-1 and 2. This study have been made previously at NASA for a particular case of an object falling in atmosphere [1], but here, I would like to extend the study to object accelerated in atmosphere, as people continue to make mistakes about it, because when you accelerate, the point called terminal velocity is reached very quickly than in case of an object falling in the atmosphere.
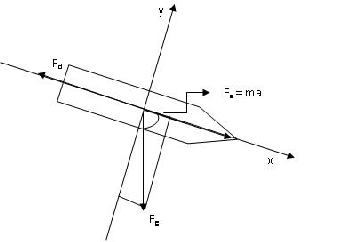
When travelling in the atmosphere, as for any system in motion, we need to identify all forces applied to the vehicle, for the object travelling in atmosphere, there is the drag force, the force resultant to acceleration we apply and the gravitational
important and its effects are really enormous.
![]()
2
Where ρ is the air density
v is the speed of the object
travelling in the atmosphere
S is the biggest section
perpendicular to the direction of the motion.
Cd is the drag coefficient
depending on the mass of the object, the atmospheric
acceleration g and the angle of attack. Its expression is:
g is the gravitational acceleration
θ is the angle of attack.
Where : m is the mass of the object
a is the acceleration applied to the object
According to the law of physics, the object will take the direction of the resultant force if the object is not in motion,
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 2
ISSN 2229-5518
if it is in motion, the object will simply accelerate or decelerate depending on the force resultant sign (positive or negative), [2]
At low speed, the drag force is very small and can be neglected, but as the speed increases, the drag force becomes very big as it is directly proportional to the speed square.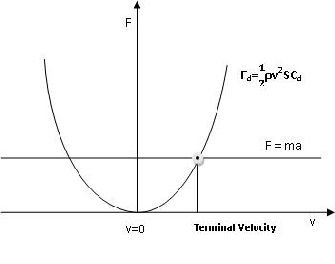
From the graphic, we can see:
d ⃗ + F g ⃗ + F a ⃗ = 0 ⃗ (First law of
a. Before the terminal velocity, we can accelerate as we want, as the force resultant to acceleration we apply plus the force resultant to the gravitational acceleration (This force depends on the angle of attack) is bigger than the drag force.
b. At the terminal velocity, the force we apply plus
the gravitation force equals the drag force. At this point the motion is uniform.
Fd = Fa + Fg
Fd = ma + mgcos 8;
Newton)
![]()
1
ρv2SC
= ma + mgcos 8;
2 d
v2 =![]()
2m(a+gcos9)
![]()
pSCd
![]()

2m(a+gcos9)
- Fd + Fa + Fg = 0 ;
Fd = Fa + Fg
Fd = ma + mgcos 8;
v =
v =
pSCd
2m(a+gcos9)
pSCd
![]()
ρv2SCd = ma + mgcos 8;![]()
2m(a+gcos9)
If we start to nnot go over this speed. This is the speed limit we cannot go over in
v2 =![]()
![]()
pSCd
2m(a+gcos9)
pSCd
atmosphere if we accelerate from zero.
c. After the terminal velocity, we cannot accelerate anymore because the drag force is bigger than the force resultant to acceleration we apply plus the force resultant to
gravitational acceleration which depends on the angle of
attack.
Fd > Fa + Fg We cannot accelerate anymore
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 3
ISSN 2229-5518
Here, it is very very dangerous, because if the speed is too high, the vehicle will explode! This is the case for Colombia, Falcon HTV-1 and 2, and Airforce Hypersonic jet Waverider if you hit atmosphere at extremely high speed, the air will form a kind of wall with a resistance force of the drag force. Let us estimate, for example , the drag force for Colombia when it was reentering the atmosphere: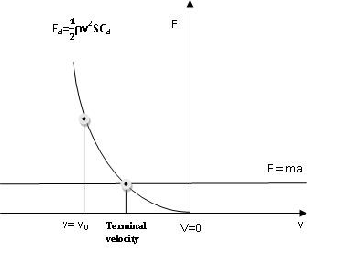
![]()
1
2
![]()
1
2
3600s = (20000000 / 3600) m/s = 5555 m/s ]
![]()
1
2
9m2 and the drag coefficient was 0.2, the air density at the
explosion of Colombia, is the meteor which exploded in the skies of Russia, it exploded when reentering atmosphere, you know how a rock is so compact, so hard to blow, but it exploded and break apart! How then Colombia could resist when rocks are exploded?
This is the same thing as for Falcon HTV-1 and 2. At the reentry, they lost their skins and engineers say that it is the extreme heat [3] or the aeroshell degradation [4] This is the air resistance which caused the vehicles to disintegrate because the drag force is too big so that the vehicles disintegrate.
According to Yunus A. (2006) [5], when you travel in the atmosphere, the air will decelerate you until you reach the speed called the terminal velocity, the deceleration force is the drag force. This force is very big so that your vehicle will decelerate very quickly. This is why Falcon HTV-1 and 2 fall in Ocean prematurely [6] and the engineers say that it is an unknown anomaly.
you can’t accelerate at all, because the drag force is far superior to the force you can apply to your vehicle, any acceleration you apply , will not accelerate it. Here for example, when the air Force’s X-51A Waverider hypersonic missile was tested, engineers accelerated, and when it didn’t accelerate, they said that the engines didn’t start[7]., The engines may have been started but because the drag force was far superior to the force resultant to their acceleration, there were no effect.
Let’s take an example of Colombia as we calculated the drag force at reentry:![]()
1
2
![]()
31 021 572 5 N
d = - 10340.5 m/s ( Assume that Colombia
m
moment was 1.1117 kg/m3]
This force is really too big, Colombia could not enter atmosphere at this speed (20000km/h), that why it exploded at reentry but until now people still say that the reason of its disintegration was a mystery! Or say that the wing was burned out. At the moment it exploded, people living in the region head a very big blast and they thought that it was a seism. Another event which explains the
mass was 3 000 kg)
This deceleration is too big, even if you accelerate, it is difficult to find an acceleration which is bigger than this deceleration. Even if you can find it, the vehicle would be compressed between two extremely big forces so that it can explode ! This is the deceleration at reentry.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 4
ISSN 2229-5518
Calculation of the speed below which you can start accelerate :
Fd = Fa + Fg![]()
Fd = ma + mgcos 8;
ρv2SCd = ma + mgcos 8;![]()
v2 = 2m(a+gcos9)![]()
pSCd
![]()
v = 2m(a+gcos9)
pSCd
![]()
![]()
v = 2m(a+gcos9)
pSCd
but if you increase the acceleration, the speed will grow quickly, so that the terminal velocity can be reached quickly. This speed is indirectly proportion to the square root of the section, so that there is also a chance to increase the terminal velocity by reducing the section. Another option would be to minimize the drag coefficient as its square root is indirectly proportional to the velocity. As we can see from this expression, it would be really difficult to achieve Mach 20, that’s why I said in the title, that Mach 20 is impossible or very difficult to achieve in atmosphere.
For example, for Falcon HTV-2, the mass required for it to be a glider and travel at the speed mach 20 must be bigger
2m a+gcos9
v =
pSCd

This is the speed below which you can start accelerate in
than:
V(mach 20) =![]()
![]()
2m(a+gcos9) ;
pSCd
atmosphere. As we can see, it depends on the square root of the mass of the vehicle and the square root of the
The acceleration is 0 as it is a glider; so that
acceleration you apply. It is also indirectly proportion to the square root of the biggest section perpendicular to the
direction of the motion and indirectly proportion to the
V(mach 20) =![]()
![]()
2m(gcos8)
pSCd
=> v2 =
![]()
2m(gcos8)
pSCd
square root of the drag coefficient.
v2 ρSCd = 2m(gcosθ) ;
m =( v2 ρSCd)/ 2gcosθ
![]()
![]()
![]()
![]()
pSCd
![]()
2x1000x(100+10cos60) =
1.117x5x0.2
![]()
![]()
20000x(10+cos60) =
1.117
=[ (5555.5)2x1.117x5x0.2]/2x10xcos60
![]()
2x1000x(10+0.5)
1.117
[ I assume that Falcon HTV – 1 and 2 weight 1000 kg, the acceleration is 100 m/s2 and the air density is 1.1117 kg/m3 and the drag coefficient Is 0.2, the biggest section perpendicular to the direction of the motion is 5m2 , you may calculate the real speed when using the real values]
As this speed is directly proportion to the square root of the mass and acceleration, you can increase it by increasing the mass and the acceleration, that’s why large planes which have big mass, this speed can be high, so to increase this speed you need to increase the mass and acceleration
= 34474929.41 kg = 34474.9 Tones. This mass is really really big for falcon htv-2 to travel at mach
At this speed (terminal velocity), the motion is uniform and even if you continue to accelerate, there will be any effect. The motion will remain uniform.
From above, we can see that it is difficult to travel at mach
20, but solutions exist: We will discuss them in coming publications.
From above discussions we can see, regardless of erodynamic design we can do, there must be a speed limit we cannot go ever in atmosphere. If we launch our vehicle from a high speed, the air will bring us to this speed limit, if we accelerate from zero, the air will not allow us to go over
this speed limit. At low velocities up to mach 3, we may
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 5
ISSN 2229-5518
neglect (but we must calculate it) the drag force, but above mach 3 we have to take in account the drag force and deal with it properly otherwise it may cause a lot damages and our usual design may not work, we may need another special kind of design which may allow us to penetrate in atmosphere. I have some proposals which I might discuss about with people who are interested.
References
[1] National aeronautics and space administration, Terminal Velocity (Gravity and Drag) [online] Available from: http://exploration.grc.nasa.gov/education/rocket/termvr.ht ml (Accessed 28 January 2013)
How we can achieve high speed, the speed of light and even higher
How we can travel in the atmosphere at high speed
(Hypersonic flights problem solved)
How we can cut expenses flying to space and building powerful airplanes.
Mwizerwa Pierre Celestin
Tel: (0086) 13522370755
E-mail: mwipice@yahoo.com
px (accessed 28 January 2013)
http://www.darpa.mil/NewsEvents/Releases/2011/08/14_D ARPA_HYPERSONIC_VEHICLE_SPLASH_DOWN_CO NFIRMED.aspx (Accessed 28 January 2013)
failure-of-htv-2-hypersonic-vehicle-23224174/
How to fly in the atmosphere conveniently, and at low price.
IJSER © 2013 http://www.ijser.org