International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 421
ISSN 2229-5518
Supply Chain Control Via Distributed Robust
Model Predictive Controllers
Romina Madani, Amin Ramezani, Mohammad Taghi Beheshti
Abstract—Companies apply supply chain management system to gain and preserve their positions in today's competitive market world. Supply chain is a united network of supply, production, storage, distribution and sales units. The aim of the control system is to keep the system in an optimal set point in presence of the uncertainties and delays which results in customer satisfaction in least time, with minimum cost and best product quality. Model predictive control (MPC) is an effective method in supply chain systems, but it lacks the capability of dealing with system model uncertainties. In supply chains, model uncertainties are significant and can easily degrade the supply chain performance. In this paper uncertainties will be added to regular supply chain models and two kind of uncertainties (plant model mismatches and bounded input uncertainties) will be controlled by distributed robust Model Predictive Controllers (DRMPCs).
Index Terms—Supply Chain, Model uncertainties, Distributed Robust Model Predictive Controller
—————————— ——————————
1 INTRODUCTION
upply chain consists of suppliers, manufacturers, distributers, warehouses and retailers to transform products from raw materials into finished goods and deliver those goods into the hand of end customers in least time, with minimum cost and the best product quality. So the supply chain is a large scale system with different subsystems that are highly coupled with each other. There are two important concepts in supply chains. One of them is safety stock (safety inventory) and the other is Bullwhip effect. Safety stock is a term used by logisticians to describe a level of extra stock that is maintained to mitigate risk of stockouts due to uncertainties in supply and demand. Adequate safety stock levels permit business operations to proceed according to their plans. Safety stock is held when there is uncertainty in the demand level or lead time for the product; it serves as an insurance against stockouts. Another concept in the supply chains is bullwhip effect. The bullwhip effect can be explained as an occurrence detected by the supply chain where orders sent to the manufacturer and supplier create larger variance than the sales to the end customer. This variance can interrupt the smoothness of the supply chain process as each subsystem in the supply chain will over or underestimate the product
demand resulting in exaggerated fluctuations.
During the last half century many mathematical tools emerging from the control literature have been applied to the supply chain management problem. These tools vary from classical transfer function analysis, optimal control methods and PID controllers to highly sophisticated control methodologies, such as model predictive control [1]. Vassian
————————————————
• Romina Madani is currently pursuing masters degree in control engineering in Tarbiat Modares University, Iran.Email:romina.madani@modares.ac.ir
• Amin Ramezani is Assistant Professor in electrical engineering in Tarbiat
Modares University, Iran. E-mail: ramezani@modares.ac.ir
• Mohammad Taghi Beheshti is Associate Professor in electrical engineering
in Tarbiat Modares University, Iran. E-mail: mbeheshti@modares.ac.ir
proposed an inventory control framework based on z- transform methodology [2]. Kapsiotis and Tzafestas were the first to implement MPC to an inventory management problem [3]; Dunbar and Desa applied a recently developed distributed implementation of MPC to the problem of dynamic supply chain management problem, using “Beer Game” theory [4]; Jie Li and Mian Peng have implemented a time stamped MPC to control a supply chain with uncertainties in customer order transmittal delay[5].
However MPC is a powerful mean in industry and supply chain, but it lacks the capability of dealing with system model uncertainties. Many methods have been proposed to solve this problem, where the LMI based Robust predictive control is quite common among them. Supply chain is a large scale problem which has uncertainties in its various parts. For example manufacturing rate and distribution rate are considered to be constant in most papers, however in practical cases these assumptions may not be hold and distribution rate and manufacturing rate may belong to uncertain but bounded sets. Another uncertainty is Customer demand which may be stochastic and have no specific structure, but is known to be bounded. Ignoring these uncertainties could have serious effects on the system. Reference number [6] is among the few papers which has considered uncertainties in supply chain model and used a centralized feedback robust model predictive controller for the system. However, for large scale systems it is better to use distributed controllers. One of the main reasons is that the state feedback controller for each subsystem in decentralized control is obviously of smaller dimensions than a state feedback controller of the centralized control strategy and this will speed up the simulations. Moreover inventory control (safety storage control) is an important issue in supply chains which is not considered in the mentioned paper. In this paper, uncertainties in distribution rate and manufacturing rate are considered as polynomial uncertainties or plant model mismatches and customer stochastic demand is considered as a bounded input uncertainty. Supply chain model is divided into different subsections, so that robust MPCs based on LMI and convex optimization can be applied for the subsystems with
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 422
ISSN 2229-5518
polynomial uncertainties and the subsystem (Retailer) which includes bounded input uncertainty will be controlled by a
d(inv k (t))
dt
= pM (t) − p k ,k "(t)
robust MPC in which a robust counter part of the uncertain
optimization problem will be derived by using YALMIPs
pM = R M t M
(3)
robust optimization feature in MATLAB software. In general each controller will do its own local optimization and will sent its optimized signals to the other coupled controllers.
2 SUPPLY CHAIN MODELING AND CONTROL STRATEGY
R Mmin ≤ R M ≤ R Mmax
k ∈{M}, k " ∈{D}
Where inv k (t) , shows the inventory level of node k
(manufacturing unit) , pM (t) is the number of the products which
2.1 Supply chain model
is produced by manufacturer. R M
is the manufacturing rate
Fig.1 illustrates a supply chain system .The supply chain
consists of suppliers (S) , manufacturers (M) ,distributers (D),
retailers (R) and final customers (shoppers) as its subsystems. For each subsystem k, an upstream subsystem k' (on the left)
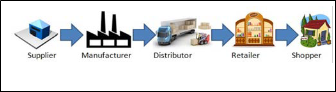
and a downstream subsystem k" (on the right) is determined. Node k' will supply node k and node K" will be supplied by node k.
Fig. 1. Supply chain echelons
Equations 1-3 are representing the system model in each of the retailer, distributer and manufacturing units.
Retailer unit model :
(units/hour) which belongs to an uncertain but bounded set and
t M is machine running time .
2.2 Supply chain control method
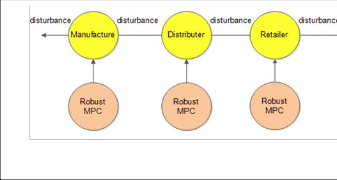
In this paper distributed Robust MPCs (DRMPCs) are used to control the supply chain. First controller corresponds to the retailer unit. This controller performs its optimization process based on customer demand and sends the optimized signals to the distribution unit as input disturbances. Second controller corresponds to the distributer unit. In distribution center despite the model uncertainties, the local optimizations will be performed and the optimized inputs will be sent to the next controller as input disturbances. Third and final controller corresponds to the Manufacturer unit. Such as two other controllers, after finishing the optimization process despite the model uncertainties, the last controller sends its optimized inputs to raw material supply unit. So all of the subsections will be controlled and the uncertainties cannot interrupt the
system smoothness anymore.

d(inv k (t)) = p dt
k ',k
(t) − W k (t)
Wmin ≤ W k (t) ≤ Wmax
k ∈{R}, k' ∈{D}
(1)
3 ROBUST MPC
3.1 Bounded input uncertainty
Consider the following system model
Where inv k (t)
shows the inventory level of node k (retailer
x(k + 1) = Ax(k) + Bu(k) + W(k)
center), p k ',k (t)
is the transferred product through (ḱ, k) channel
y(k) = cx(k)
(4)
and W k (t)
represents the consumer demand which belongs to an
uncertain but bounded set.
Distributer unit model:
Wmin ≤ W(K) ≤ Wmax
In many cases, control engineers do not have a-priori knowledge of the disturbance but only know its range.

d(inv k (t)) = p dt
D k ',k
(t) − p
k ,k "(t)
Equation (4) describes these systems. We are looking for a control law that gives good performance for every possible
disturbance from this uncertainty model. Equation (1) is a
pD k ',k = R Dk ',k ND
R Dmin ≤ R Dk ',k ≤ R Dmax
k ∈{D}, k ' ∈{M}, k " ∈{R}
(2)
practical example of these systems. After discretizing (1), its total structure will be similar to (4).The objective is to stay output as close as possible to the desired level while
guaranteeing that
y ≤ ymax
is satisfied despite the unknown
Where
inv k (t) , shows the inventory level of node k
but bounded disturbances W.
(distribution center) ,
pD k ',k (t) is the number of the products
Various formulations for robust MPC and handling bounded
(units) which should be distributed by distribution center at
input uncertainties was introduced in [7] . To speed up the simulations we will use YALMIPs robust optimization feature
rate
R Dk ',k (units/van).
R Dk ',k belongs to an uncertain but
in MATLAB software (Using "ROBUSTIFY" command) to
bounded set and ND represents the number of the vans which
are needed.
Manufacturer unit model:
derive a robust counter part of the uncertain optimization problem and to handle uncertain inequalities. For more information the reader is referred to YALMIP WIKI Site.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 423
ISSN 2229-5518
3.2 Polynomial uncertainty
Kothare et al. (1996) proposed a methodology for robust centralized constrained MPC design that maintains robust stability and minimizes a bound on performance in the presence of model errors. The problem is formulated as a convex optimization problem with linear matrix inequalities (LMI) ,[8].
u(k) = Fx(k)
x(k + 1) = (A + BF)x(k)
Step 4: k+1 ← K and go to step 2
4 SIMULATIONS
(11)
Consider the following system model
x(k + 1) = A(k)x(k) + B(k)u(k)
y(k) = cx(k)
[A(k) B(k)] ∈Ω
(5)
A three echelon supply chain system is used in simulated example. The echelons are manufacturer, distributer, and retailer. Whole simulation time is 60 time unit (day), the prediction horizon time is 30 and the control horizon time is
10. The model uncertainties such as distribution rate ( R D ),
manufacturing rate ( R M ) and customer order rate ( W k )
Matrices A(k) and B(k) belong to the following convex set Ω
with L vertices.
belong to unknown but bounded sets between 70-120 (units/day), 50-100 (units/van) and 70-100 (units/day)
respectively. The nominal rates for R D and R M are 80 and 100.
Ω = CO{[A1
B1 ], [A2
B2 ] ,, [AL
BL ]}
(6)
Output and input Weights that are used to tune Model
Where “CO” refers to the convex hull and the following
equations are satisfied
predictive controllers, Inventory set points (safety storage), and initial inventory levels are given in table one
[A B] = ∑ l
λ [A B ]
, λ ≥ 0, ∑
λ = 1
(7)
i =1
i i i i
i =1 i
TABLE I. SUPPLY CHAIN DATA
Cost function is defined as a Min-Max optimization problem.
J = ∑ p x(k + i) Q x(k + i) + u(k + i) Ru(k+ i)
i = 0
1
min
max
J(k)
(8)
u(k + i), i = 0,1,..., Np
[A(k + i) B(k + i)] ∈Ω
It is proved that this problem can be converted into a LMI
based robust control problem as follows:
minγ
γ ,Q,Y
Simulations will be done with two Control methods. one with
1 x(k)T
≥ 0
implementation of distributed Robust MPCs and considering
x(k) Q
T 1/ 2
1/ 2 T
all model uncertainties (Fig.2) and the another one is
implementation of distributed standard MPCs and nominal
Q (A jQ+ B jY)
Q(Q1)
(R Y)
(9)
rates (Fig.3 )
A jQ + B jY Q 0 0 ≥ 0
1/ 2
(Q1) Q 0
γI 0
R1/ 2Y 0 0
2
γI
u max
Y
≥ 0,


u(k +i|k) ≤
Y T
Q 2
u max
After solving the convex optimization problem, the matrices Y and Q are achieved and control gain can be calculated using (10).
F = Y −1Q
(10)
Fig. 2. Method 1: Implementation of Distributed Robust MPCs on Supply Chain Management
Thus, the overall LMI based robust model predictive control algorithm can be expressed as following steps:
Step1: Specify the initial value x (0)
Step2: calculate the control gain using equation (10).
Step3: calculate the state and input variables using equations
(11):
IJSER ©
http://www.ij
International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 424
ISSN 2229-5518
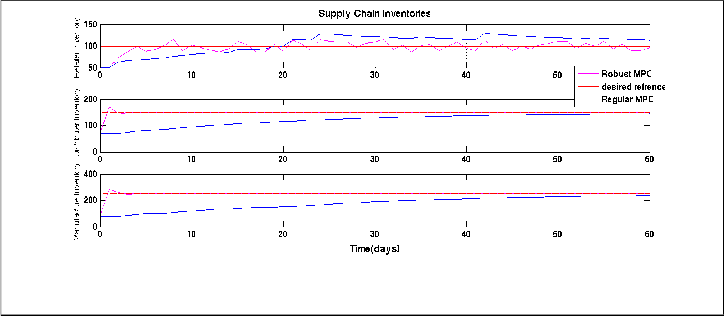
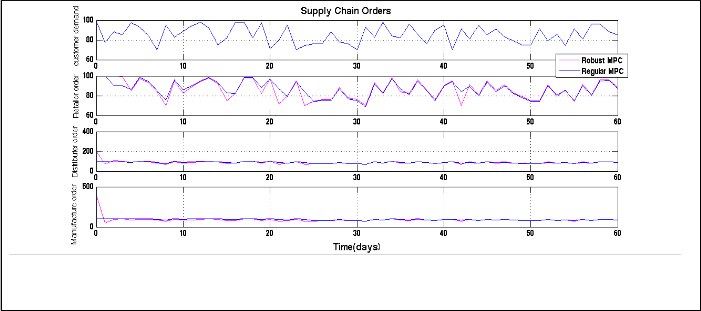
Fig 4 shows Inventory levels in all echelons which are achieved by two control methods. It can be seen that by using RMPCs, the inventory level in first echelon (Retailer) is fluctuating in certain small domains around its predetermined safety stock (desired reference) and for two other echelons (Distributer and Manufacturer), the desired inventory levels are tracked after around three days; however, by implementing regular MPCs, the desired inventory levels are tracked after long time horizon (more than 60 days for first echelon and 50 days for two other
echelons). It means that, in the presence of model uncertainties, the distributed RMPCs can easily handle inventory and safety stock control and play better performance on inventory control than the method with regular MPCs and nominal rates. Customer orders which are sent to upstream echelons are illustrated in Fig.5. As it mentioned before, from control engineering perspective, these orders are manipulated inputs (signal controls) which are achieved by local optimization of Model Predictive Controllers. As it can be seen, the signal controls which are achieved by two methods are similar to each other and the only considerable difference is in the initial control efforts which are stronger in first method (DRMPCs) than second method (regular DMPCs) . To conclude, Demand variability rate from customer to supplier or the bullwhip effect has been successfully controlled by two methods, but the first method (implementation of DRMPCs) has used these signal controls in a more efficient way than second method (regular DMPCs) to handle inventory control.
Fig .4. Supply chain inventory control ( safety storage control) vie two control methods (Distributed Robust MPCs and
Distributed regular MPCs)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 425
ISSN 2229-5518
Fig .5. Supply chain order rates vie two control methods (distributed Robust MPCs and distributed regular MPCs)
5. CONCLUSION
Supply chain is a large scale problem which has uncertainties in its various parts .Uncertainties in supply chain model could seriously affect the performance of the system. In this paper, model uncertainties are added to regular supply chain models. Due to these model uncertainties and large scale characteristic of supply chain, distributed robust Model Predictive Controllers (DRMPCs) are implemented. The simulation results show that in the presence of model uncertainties the distributed RMPCs play better performance on inventory control than regular distributed MPCs . Also optimal customer orders in each echelon and bullwhip effect control are successfully achieved in the presence of model parametric uncertainties.
REFERENCES
[1] Sarimveis, H., Patrinos, P., Tarantilis, D., Kiranoudis,T. " Dynamic modeling and control of supply chain systems," A review. Computers and Research, Vol. 35, pp. 3530 – 356, 2008.
[2] Vassian JH. "Application of discrete variable servo theory to inventory control," Operations Research; 3:272–82, 1955.
[3] S. Tzafestas, G. Kapsiotis, and E. Kyriannakis, “Model-based predictive control for generalized production planning problems,” Computers in Industry, vol.34, no.2, pp.201-210, 1997.
[4] du W. B. Dunbar., S. Desa., “Distributed MPC for dynamic supply chain management,” in Assessment and Future Directions of Nonlinear Model Predictive Control, Springer,pp. 607–615 , 2007.
[5] J. Li., Y. Chai., and M. Peng., “Time-stamping Predictive Strategy for Multi-echelon Inventory Control with Uncertain Lead Time,” Int. J. Inf. Manag. Sci., pp. 273–286 , 2012 .
[6] X. Li and T. E. Marlin, “Robust supply chain performance via Model
Predictive Control,” Computer and Chemical Engineering., vol. 33, no.
12, pp. 2134–2143 , 2009.
[7] J. Löfberg. Minimax Approaches to Robust Model Predictive Control.
PhD thesis no. 812, Linköping University, Linköping, Sweden, 2005. [8] M. V. Kothare, V. Balakrishnan, and M. Morari, “Robust constrained
model predictive control using linear matrix inequalities,”
Automatica, vol. 32, no. 10, pp. 1361–1379 , 1996.
IJSER © 2014 http://www.ijser.org




