International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 338
ISSN 2229-5518
Static Voltage Collapse Studies
In Power Systems
D. Vijaya Kumar , B.Manmadha Kumar , I.Ramesh , A.Jagannadham
—————————— ——————————
I INTRODUCTION
ORE and more voltages related problems are being experienced by modern power systems in India as well as in other foreign countries. It is well known that the
voltage problems are closely related to the management of reactive power resources and flows in the system. It has been established that quite a few of the grid failures experienced by different electric utilities have been caused by the voltage collapse phenomenon [10]. The study of a system for voltage instability/collapse conditions will have to be done both from the planning as well as from the operation viewpoints [13]. The present study mainly concentrates on the planning aspects.
Lack of adequate reactive power resources in a power system is a major contributing factor to the process of voltage collapse. As loads in a power system increase, voltage across the network tends to decrease and reactive power, losses increased. The increased reactive power demand would be supplied by voltage regulating devices such as generators or static var compensators, if possible [1]. However, due to physical limitations, such devices cannot supply unlimited amounts of reactive power. Often sustained load growth will result in some source of reactive power, or perhaps a number of such sources, encountering limits, i.e. reaching a physical limitations in the amount of reactive power that they can supply.
————————————————
• DVijaya Kumar is Professor in Department of E.E.E, Aditya Institute of
Technology and Management, Tekkali, Andhra Pradesh, India.
• I.Ramesh and A.Jagannadham are Assistant Professors in Department of
E.E.E, Aditya Institute of Technology and Management, Tekkali, A.P, India.
Once a reactive power source has reached its maximum limit, it can no longer regulate the voltage. Therefore, sustained load growth results in accelerated voltage decay and hence greater reactive power requirements. This may force other voltage regulating devices to their limits, with subsequent further accelerations in the rate of decline of Voltage. If load is increased further, the point of voltage collapse would soon be reached. This phenomenon has come to be known as voltage collapse.
A voltage collapse process may consist of the following steps: [10]
a) The critical disturbance by increasing transmission line loading would develop and untenable increase of series reactive power losses I2 X.
b) This would cause a sharp voltage reduction at a number of transmission load substations.
c) By reducing loads and provoking over excitation in surrounding units, the voltage reduction would create and initiate stability.
d) But the voltage reduction would also initiate a powerful destabilizing force, automatic on-load transformer tap changing, which would progressively increase the loads, and may even provoke load overshoot.
e) This load increase caused by each tap changing step would progressively reduce the transmission voltage levels.
f) Each voltage reductions would increase series reactive power losses inversely to the voltage cubed.
g) This changing situation could only maintain stability until the first units’ over excitations protection functions.
h) Once this occurs, the voltage falls so sharply that system collapse is inevitable.
i) The sustained excess, reactive demand would disrupt inter unit co-ordinations so leading to angle instability as the final cause of breakdown.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 339
ISSN 2229-5518
The objective of this paper is to develop the necessary
background for the analysis of static voltage collapse problem, establishing the concepts of P-V/Q–V curves (nose curves). Voltage sensitivity to reactive power, number of solutions at different load levels, the point of collapse (PoC) and the condition which occur at voltage collapse in a simple, single line loss-less power system, and then to generalize to a multi- bus system. The issues of sensitivity of voltage to load power on the upper and lower sections of the nose curve and the
The Fig. 2 illustrates the following ideas.
![]()
dV
![]()
dPd V <0
This shows that an increase in Pd at V1 will cause a decrease in voltage and a decrease in Pd will cause an increase in voltage. This is an expected behavior in normal power system operation and is usually termed as stable solution, upper branch solution or high voltage solution.[1, 2].![]()
dV
change of number of solutions as the load power is changed is explored in this paper.![]()
dPd
V2 > 0
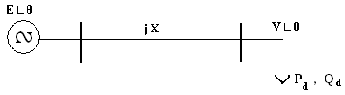
Consider a single line, loss-less system with constant load and fixed sending end voltage, E. This assumption of fixed sending end voltage amounts to limit-less reactive power supply from the generator to keep the generator terminal voltage fixed at E at different load conditions. This section will establish the nose curves, voltage Sensitivity to reactive power, number of solutions at different load levels and the point of collapse in the two-bus system.
The sensitivity of V to Pd at solution point V2 is opposite
to that at V1 . This is called an unstable solution, lower branch
solution or low voltage solution.
It could be seen that the number of solutions various as Pd
is increased. It can be visualized from figure 2 that there will
be:
Fig.1. Lossless Two Bus System
The active and reactive power balance equations are:
EV
i) 2 Solutions for Pd < Pd max
ii) 1 Solution at Pd = Pd max
iii) No Solution for Pd > Pd max
The point (Pd max, V C ) on the P d – V diagram, is the Point of
Collapse![]()
dV
![]()
dPd Vc
Pd =
Q d =
− P =
− Q =
![]()
− Sin θ
X
V 2 EV
![]()
![]()
− +
X X
Cos θ
(2)
(1)
This indicates that voltage is infinitely sensitive to Pd at Vc . Similar results can be obtained for Qd also.
From
euqation
E 2
(1)
For a single line network, the criterion for voltage stability
Pd =![]()
Sin 2θ
2X
(3)
is stated as follows
dV dV
E 2![]()
P = at
θ = 45 0
(4)![]()
![]()
> 0 > 0 dP dQ
(5)
d max 2X
Where P = - Pd
and Q = -Qd.
The point (Qdmax, V C ) is the PoC on Q d –V diagram. The condition for voltage collapse is thus;
dV dQ
![]()
![]()
= ∞ (or) = 0
dQ dV
dV dP
![]()
![]()
= ∞ (or) = 0
dP dV
Thus an alternate statement for voltage collapse can be given as: A Power system in steady state is at a point of voltage
ΔVj
Fig.2. Pd – V Diagram
collapse if some![]()
ΔQ k
is unbounded as ∆Qk tends to zero.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 340
ISSN 2229-5518
Using bus frame of reference, the bus current at ith bus is
dp = J
dq
dθ
dv
+ J λ
dλ = 0
(16)
expressed as [3]:
n
Where J is given by
I i =
∑Yik Vk
; For i
= 1, 2, ........n
(6)
=dp
− P *
J Pλ
k =1
The complex power at ith bus
J = dλ =
dq
=
(17)
![]()
− Q *
J Qλ
S = V I *
= V ∑
Y * V * ;
For i
= 1, 2, ........n (7)
dλ
i i i i
efine
ik k
D
Therefore it gives the direction of loading from equation
(16)
Vi = |Vi |ejѳ ;
θik = θ i - θ k ;
dθ
dv
= − J −1
[J λ ]dλ
(18)
Yik = Gik + jBik; Si = P iSP + jQiSP Then
So λ can be increased until J becomes singular. The point of
voltage collapse therefore corresponds to the singularity of J, i.e.,det J = 0![]()
![]()
![]()
P (x) = ∑ V V [G
Cos(θ − θ
) + B
sin(θ − θ
)]
VOLTAGE SENSITIVITY
i i k ik
![]()
![]()
[
i k ik
i k
(8)
The linearised power flow equation is re-written in a modified
form as:
Q i (x) = ∑ Vi Vk
G Sin(θ − θ ) − B sin(θ − θ )]
ik
Δp
= J Pθ
J PV
Δθ
For i=1,2,3, …n.
Define mismatch vector for real and reactive power as:
Δq
J qθ
J QV
Δ ![]() V
V ![]()
(19)
Using equation (16) and assuming that there is no angular
Pi (x) = Pi (x) - Pi SP (9)
instability, i.e., det J
Pθ≠0
Qi (x) = Qi (x) - Q iSP (10)
Equations (9) and (10) can be expressed in compact form as:
If λ is set equal to E, the generator terminal voltage dV = - J QS -1 (J Qe - J Qθ J Pθ-1 J Pe ) dE (20)
f ( x) =
p(x) = 0
q(x)
(11)
∂q
![]()
Where J Qe =
∂E
and
![]()
∂P J Pe = ∂E
Let X = Xe + Δx, then by Taylor series expansion.
If λ is set equal to b, the susceptance of SVC at the load bus
(Qd = -b V2) and
dV = J QS -1 (J Qb - J Qθ J Pθ-1 J Pb ) db = - J QS -1 J Qb db (21)
F(x) = f(xe +Δx) = f(Xe )+J(Xe )ΔX + higher order terms (12)
Choose Δ x such that f(x) =0 and ignoring the higher order
∂P
![]()
As J pb =
∂b
= 0 and
∂q
![]()
G b = ∂b
terms of the expansion,
Δx = -J-1(xe) f(xe) (13)
Where J(xe) the Jacobian evaluated at Xe , Expressed as an
Thus, in single line case, in addition to the condition given by equation (5) for voltage stability, the following are also to be satisfied.
iterative scheme, the next estimate of state vector is Xi+1 = Xi +
ΔXI , the iterative method of solution continues until mismatch functions satisfy a pre-determined tolerance between
dV dV
![]()
![]()
> 0, > 0
dE db
(22)
successive iterations.
The power flow equation in the case of multi-bus system
can be written as
P(θ, V, λ) = P((θ, V) – PSP – λ P* = 0 (14)
Q(θ, V, λ) = Q((θ, V) – QSP – λ Q* = 0 (15)
Where λ is the loading parameter and
In a multi – bus system the sufficient condition for voltage
stability is that all elements of J Qs -1 , -(J Qe - JQθ J Pθ-1 J Pe ) and – (J Qb - J Qθ J Pθ -1 J Pb ) are positive when there is no angular stability problem.
The relationship between voltage sensitivity to parameter λ, A
similar relationship can be established between θ and λ.
Using equation (15):
dp dp
J PO
J PV
dθ
J Pλ
P* =
− and
![]()
Q * = −
+
dλ
= 0 (23)
![]()
dλ dλ
J Q0
J QV
dv
J qλ
Linearization of equations (14) and (15) yields,
From equation (23)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 341
ISSN 2229-5518
dV = -J QV-1 (J Qθ dθ + J Qλ dλ) (24)
dθ = - (J PS -1 (J Pλ – J PV J QV-1 J Q λ) dλ (25)
If det J QV ≠ 0, then det J = 0 implies det J PS = 0 and equation (25) shows that angular sensitivity to parameter λ is infinite when det J = 0.
Thus it is seen that in general angle and voltage stability
issues are interrelated.
A Power system is voltage stable, at a given operating
condition, if for every bus in the system, bus voltage magnitude increases as reactive power injection at the same bus is increased. A system is voltage unstable if, for at least one bus in the system, bus voltage magnitude decreases as the reactive power injections at the same bus is increased. In other words, a system is voltage stable if V-Q sensitivity is positive for every bus and unstable if V-Q sensitivity is negative for at least one bus.
The linearised steady state system power voltage equations are given by equation (19)
Bus Participation Factor:-
The relative participation of bus k in mode is given by bus participation factor.
Pki = ζ ki η ik
Where Pki indicates the contribution of the ith eigen value to
the V _ Q sensitivity at bus k. The bigger the value of Pki , the more λi contributes in determining V – Q sensitivity at bus k. For all the small eigen values, bus participation factors determine the areas close to voltage instability. Bus participation factors determine the areas associated with each mode. The size of the bus participation in a given mode indicates the effectiveness of remedial actions applied at that bus in stabilizing the mode. The sum of all the bus participation for each mode is equal to unity.
Branch Participations:-
When the change in reactive power injections in Δ Qmi, the
resulting voltage variations is ΔVmi and the model angle
variation is,
ΔP
J P θ
J PV
Δθ
Δθmi = -J-1 pθ J pv ΔVmi
ΔQ =
Where
Q θ
J
Qv
ΔV
(26)
With ΔV and Δθ known, the linearised reactive loss variation across transmission branch 1j, ΔQ1ji, and the linearised reactive power output variation at generator gk, ΔQgki, can be
ΔP = incremental change in bus real power
ΔQ = incremental change in bus reactive power injection. Δθ = incremental change in bus voltage angle.
ΔV = incremental change in bus voltage magnitude.
System voltage stability is affected by both P & Q. However, at each operating point P is kept constant and
calculated, Let,
Δθ1maxi = maxj ΔQ1ji,
Δθgmaxi = Maxk ΔQgki,
The participation factor of branch ij to mode I is defined as,
ΔQ
voltage stability is evaluated by considering the incremental
relationship between Q and V. Although incremental changes in P are neglected in the formulation, the effects of change in
P1ji =
1ji
![]()
ΔQ1maxi
(29)
system load or power transfer levels are taken into account by
studying the incremental relationship between Q and V at different operating conditions.
let ΔP = 0 then,
ΔQ = (J qv - J qθ J-1 pθ J pv) ΔV (27)
= J R ΔV
And
ΔV = J-1 R ΔQ (28)
J R is called the reduced Jacobian matrix of the system; J R is the
matrix which directly relates the bus voltage magnitude and
bus reactive power injections. Eliminating the real power
Branch Participations thus indicate, for each mode, branches consume the most reactive power for a given for a incremental change is reactive load. Branches with high P1ji are those which cause mode I to be weak. The branch participation thus provides valuable information regarding.
i. Remedial actions in terms of transmission branch
enhancement and redistributing the power flow to alleviate the loading on that branch,
ii. Criteria for contingency selection,
The participation factor of generator gk to mode i is defined
as, incremental change in system reactive loading i.e
ΔQ
and angle part from the system steady state equations allows one to concentrate on the study of the reactive demand and
gki
![]()
P =
ΔQ gmaxi
(30)
supply problem of the system as well as to minimize
computational efforts.
Generator participations provide important information’s regarding proper distribution of reactive reserves among all
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 342
ISSN 2229-5518
machines in order to maintain an adequate voltage stability margin.
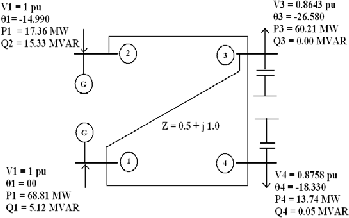
A Computer program has been developed to conduct the modal analysis of the system. The program is tested with the small system shown in Fig. 3 the test is conducted in such a way that, the operating points are varied by implementing a step change in reactive power at bus 3 (in steps of 0.05 p.u), starting from 0 p.u and incrementing until, the load flow fails to converge.
Fig.3. Four Bus Two Generator Test System
The results obtained at different operating conditions are presented in the Table.1.
TABLE I
Model Analysis Results at Different Operating Points
The fundamental aim behind this paper is to develop some tools which help in predicting the behavior of a complex system with respect to system wide voltage related performance as the loading on encounter their limits. The thesis work done establishing of effect of reactive power on the voltage stability of a power system. The work done is established on a sample 4 bus test system.
The Eigen value analysis method normally known as the
modal analysis is used for this study. It is observed that as
and when the reactive power is increased on a PQ bus, the minimum value of the Eigen values is decreasing which indicates that the stability of the system is decreasing and when the system is unstable the Eigen value becomes zero.
The study was supported by many other factors such as the
bus and branch participation factor and voltage sensitivity which gives a measure of the system stability.
[1] P.Kundur, “Power Systems stability and Control”, Mc.Graw Hill Inc.
New York. 1993 (Book).
[2] C.W. Taylor, “Power system voltage stability”, Mc.Graw Hill
International Editions; New York, 1994 (Book)
[3] A.R. Bergen, “Power System Analysis”, Prentice – Hall Inc.
Englewood Cliffs, New Jersey 07632, 1986 (Book)
[4] I.A. Hiskens, D.J.Hill, “Energy Functions, transient stability and voltage behavior in power systems with non-linear loads,” IEEE Trans on Power Systems, Vol.4, No.4, Oct 1989, PP. 1525-1533.
[5] P.A. Lof, et.al., “Fast calculations of a voltage stability index”, IEEE Trans. On Power Systems, Vol. 7, No.1 February, 1992.
[6] B.Scott, “Review of load – flow calculations methods”, IEEE Proceedings Vol. 62 No.7, pp 916-929, July 1974.
[7] B.Gao, G.K.Marrison, P.Kundur, “Voltage Stability Evaluation using modal Analysis”, IEEE Trans and power systems, Vol.7, No. 4, pp.1529-1545, November, 1992.
[8] Voltage stability of power systems: Concepts analytical tools and industry experience”, Report prepared by IEEE working group on voltage stability, 1990(Book).
[9] K.Walve, Modelling of power systems components at severe disturbances”, CIGRE report 38-18, Paris, August, 27-September,4,
1986.
[10] W.R.Lachs, “Voltage Collapse in EHV Power Systems”, IEEE paper
A 78057 – 2, 1978 IEEE/PES Wister meeting, New York, Jan/Feb.
1978.
[11] V.Aijarappu and C. Christy, “The Continuation Power Flow: A tool for steady state voltage stability analysis”, IEEE PICA conference proceedings, pp-304-311, May, 1991.
[12] N. Flatabo, R.Ogenedal, and T. Carlsen, “Voltage Stability conditions in a power transmission systems calculated by sensitivity methods”, IEEE Trans. On power systems, Vol. 5, No.4, pp-1286-1293, November, 1990.
[13] Y.Tamura, H.Mori and S. Iwamoto, Relationship between voltage instability and multiple and flow solutions in electric power
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
systems;, IEEE Trans. On power systems. Vol. PAS102, No.5, pp,llS-
1125, May, 1983.
343