International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 746

ISSN 2229-5518

Solving multi-objective Intuitionistic linear programming using Triangular Intuitionistic fuzzy number

First Author, Second Author

Abstract— This paper provides an algorithm for solving a multi-objective Intuitionistic fuzzy linear programming problem with data as triangular intuitionistic fuzzy numbers. Here, the multi-objective Linear programming problem is converted into a single objective linear programming and the problem is defuzzified using Triangular Intuitionistic fuzzy numbers. Then it is converted into equivalent crisp linear problems, and are solved using simplex method. A numerical example is provided to show the efficiency of the methodology.

Index Terms— Intuitionistic Fuzzy Sets,Triangular Intuitionistic fuzzy number,Membership and Nonmembership,Value,Ambiguity and Score value

1. Introduction

Linear Programming is one of the most important operations research techniques. It has been applied to solve many real world problems. An application of fuzzy optimization techniques to linear programming problems with multiple objectives has been presented by Zimmermann. It is extended to IFO by Attanassov.
The Intuitionistic fuzzy set (IFS) is an extension of fuzzy set (FS) where the degree of non- membership denoting the non-belongingness to a set is explicitly specified along with the degree of membership of belongingness to the set. Unlike the FS where the non-membership degree , in IFS , the membership and nonmebership degrees are more or less independent and related only by that the sum of two degrees must not exceed one.

————————————————

• Dr.R.Sophia Porchelvi,Associate Professor,A.D.M College for

Women,Nagappattinam,sophiaporchelvi@gmail.com

• S.Rukmani,Assistant Professor,S.T.E.T Women’s

College,Mannargudi,rukuthiagu@gmail.com
Recently, Li[1] has proposed a ratio ranking method for triangular intuitionistic fuzzy numbers. Then, it is applied to solve MADM problems. To this end, the value and ambiguity of TIFNs are used to obtain a new ranking approach. Using similar idea,Salahshour[6] proposed other new ranking approach for TIFNs based on the value and ambiguity. However, this approach is completely differ from Li’s method. For ranking TIFNs, concert each TIFNs to the related TFNs based on its membership function and non-membership function. Then, for each obtained TFN we applied a new defuzzification to derive a real value related to the original TFN.
The organization of the paper is as follows.Some basic definitions and properties of Triangular Intuitionistic fuzzy numbers relevant to the present work and a new ranking function are given in section 2. In section 3, an algorithm is proposed to solve the multi-objective Intuitionistic linear programming problem. A numerical example is provided in section 4 and the
paper is summarized in section 5.

International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 747

ISSN 2229-5518

2.Preliminaries

Definition:1

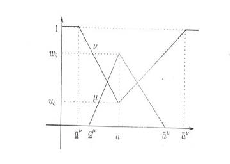
An Intuitionistic fuzzy sets (IFS) 𝑎� assigns to each element x of the universe X a membership degree
𝜇𝑎� (𝑥)𝜖[0,1] and a non-membership 𝜈𝑎� (𝑥)𝜖[0,1] such that 𝜇𝑎� (𝑥) + 𝜈𝑎� (𝑥) ≤ 1 . An IFS 𝑎� is mathematically, represented as {< 𝑥, 𝜇𝑎� (𝑥), 𝜈𝑎� (𝑥) >/𝑥 ∈ 𝑋}.
The value𝜋𝑎� (𝑥) = (− 𝜇𝑎� (𝑥)) − 𝜈𝑎� (𝑥) is called
the degree of hesistancy or the intuitionistic index of x
to 𝑎�.

Definition:2

The same is depicted in Fig 1,

Figure 1: Triangular Intuitionistic Fuzzy Number

(TIFN)

A TIFN 𝑎� = {� a

𝜇

, 𝑎, 𝑎�𝜇 , 𝑤𝑎� �, ( a

𝜈

, 𝑎, 𝑎�𝜈 , 𝑢𝑎� )}is

Definition: 3

an IFS in ,whose membership and non-membership
functions are respectively defined as,
Let �𝑎 = {�𝑎𝜇 , 𝑎, 𝑎�𝜇 , 𝑤𝑎� �, (𝑎𝜗 , 𝑎, 𝑎�𝜈 , 𝑢𝑎� )} be a TIFN. Then the value and ambiguity of 𝑎� are given as follows.

(x - 𝑎 μ)𝑤𝑎� , 𝑎 μ
≤ x ≤ 𝑎
(i) The value of the membership function of
𝑎� is ,
𝜇𝑎 (𝑥)=
𝑤𝑎� x = 𝑎

(𝑎�𝜇 – 𝑥)𝑤𝑎� , 𝑎 < x ≤ 𝑎�𝜇

(𝑎�𝜇−𝑥)𝑤𝑎�

𝑉𝜇 (𝑎�) =

�𝑎𝜇 + 4𝑎 + 𝑎�𝜇 �𝑤𝑎�
6
0, otherwise

𝑎 − 𝑥 + 𝑢𝑎� (𝑥 − 𝑎𝜗 ), 𝑎𝜗 ≤ x ≤ 𝑎
𝑢𝑎� , x = 𝑎
While the value of the non-membership function
is,

�𝑎𝜗 + 4𝑎 + 𝑎�𝜗 �(1 − 𝑢𝑎� )
𝑉𝜗 (𝑎�) = 6
𝜗𝑎� (𝑥)=

𝑥−𝑎+𝑢𝑎� (𝑎�𝜗−𝑥)

𝑎�𝜗−𝑎

, 𝑎 < x ≤ 𝑎�𝜗
(ii) The ambiguity of the membership

function of 𝑎� is

0, otherwise
𝐴𝜇 (𝑎�) =

�𝑎�𝜇 −𝑎𝜇�𝑤𝑎�

The values 𝑤𝑎� and 𝑢𝑎� respectively represent the maximum degree of the membership and non-
membership such that 0 ≤ 𝑤𝑎� ≤ 1 , 0 ≤ 𝑢𝑎� ≤ 1 and 0 ≤ 𝑤𝑎�
+ 𝑢𝑎� ≤ 1.
While the ambiguity of the non-membership function
of 𝑎� is

𝐴 (𝑎�) = �𝑎�𝜗−𝑎𝜗�(1−𝑢𝑎� )

𝜗

International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 748

ISSN 2229-5518

3.The Proposed Algorithm

1. To find the solution of a multi-objective intuitionistic fuzzy linear programming
problem, Define 𝑎� = {�𝑎𝜇 , 𝑎, 𝑎�𝜇 , 𝑤𝑎� �, (𝑎𝜗 , 𝑎, 𝑎�𝜈 , 𝑢𝑎� )} and 𝑏� = {�𝑏𝜇 , 𝑏, 𝑏�𝜇 , 𝑤𝑏� �, (𝑏𝜗 , 𝑏, 𝑏�𝜈 , 𝑢𝑏� )}

2. Convert the multi-objective IFLP into a single objective IFLP using

Where,
C1 = 5� = {(4,5,6;3/4)(4,5,6.1;1/4)}
C2 = 3� = {(2.5,3,3.2;1/2)(2,3,3.5;1/4)}
P1 = 2�5 = {(19,25,33;0.9)(18,25,34;1)}
P2 = 4�8 = {(44,48,54;0.9)(43,48,56;1)}
Subject to
𝑎� + 𝑏� = {�𝑎𝜇 + 𝑏𝜇 , 𝑎 + 𝑏, 𝑎�𝜇 + 𝑏�𝜇 ; min{𝑤𝑎� , 𝑤𝑏� }�,
a11
= 4�
= {(3,5,4.1;1)(3,4,5;0)}
�𝑎𝜗 + 𝑏𝜗 , 𝑎 + 𝑏, 𝑎�𝜗 + 𝑏�𝜗 ; min{𝑢𝑎� , 𝑢𝑏� }�}
a12
= 3� = {(2.5.3.3.5;3/4)(2.4,3,3.6;1/5)}
3. Defuzzify the IFLP into a crisp linear programming using
The value of P(𝒂�) ,
P(𝑎� )= 𝑆𝜇 (𝑎� ) − 𝑆𝜈 (𝑎� )

Where, 𝑆 (𝑎� ) = 𝑉𝜇 (𝑎� )

1+𝐴𝜇 (𝑎� )

𝑉𝜈(𝑎�)

a21 = 1� = {(0,1,2;1)(0,1,2;0)}
a22 = 3� = {(2.8,3,3.2;3/4)(2.5,3,3.2;1/6)}
b1 = 1�2 = {(11,12,13;1)(11,12,14;0)}
b2 = 6� = {(5.5,6,7.5;3/4)(5,6,8.1;1/4)}
For, converting multi-objective into single
objective,
𝑆𝜈 (𝑎� ) =

1+𝐴𝜈(𝑎�)

X1 =C1 +P1

4. Formulate the linear programming problem.
5. Solve the LPP by any one of the used simplex procedure.

4. Numerical Example

Max 5� 𝑥1 + 3� 𝑥2
Max 2�5𝑥1 + 4�8𝑥2
Subject to
4� 𝑥1 + 3� 𝑥2 ≼ 1�2
1� 𝑥1 + 3� 𝑥2 ≼ 6�
𝑥1 + 𝑥2 ≥ 0

={(4+19,5+25,6+33;min{3/4,0.9})(4+18,5+25,6.1+34;ma x{1/4,1})}

= {(23,30,39;3/4)(22,30,40.1;1)} Similarly,
X2 = C2 + P2 = {(46.5,51,57.2;0.5)(45,51,59.5;1)}
For,defuzzification,
X1 = {(23,30,39;3/4)(22,30,40.1;1)}
𝑉𝜇 (𝑎� ) = 22.75 , 𝑉𝜈 (𝑎� ) = 0
𝐴𝜇 (𝑎� ) = 4, 𝐴𝜈 (𝑎� ) = 0

International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 749

ISSN 2229-5518

𝑠𝜇 (𝑎� ) = 4.55, 𝑆𝜈 (𝑎� )
Therefore, P(X1 ) = 4.55
Similarly,
P(X2 ) = 9.2137
P(a11 ) = 0.8775
P(a12 ) = -0.018
P(a21 ) = 0
P(a22 ) = 0.005
P(b1 ) = 3.14755
P(b2 ) = 0.47073
Therefore the crisp linear programming is
Max 4.55x1 + 9.2137x2
Subject to 0.8775x1 – 0.018x2 ≤ 3.14755
0x1 + 0.005x2 ≤ 0.47033
x1 , x2 ≥ 0
Using simplex method,the optimum feasible solution is
obtained and is given by

x1 = 5.518 , x2 = 94.146 , Max Z = 892.53

Conclusion

This paper is useful to solve the multi-objective intuionistic linear programming Problem. It is also helps to defuzzification of TIFNs. An algorithm is proposed for solving mult-objective linear programming problem and a numerical example is given to show the efficiency of the

methodology.

References

1. D.F.Li, A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problem, Computer and Mathematics with Applications 60(2010) 1557-
1570
2. Dipti Dubey, Aparna Mehra, Linear Programming with Triangular Intuitionistic Fuzzy numbers, EUSFLAT-LFA (July 2011)
3. H.J.Zimmermann, Fuzzy programming and Linear programming with several objective functions, Fuzzy sets and systems.
4. S.Muruganandam, Dr.R.Nallaswamy, A multi- objective fuzzy assignment problem, Advances in fuzzy sets and systems.
5. S.Muruganandam, Dr.R.Nallaswamy, A two- objective fuzzy assignment problem, International Journal of Mathematical Sciences.
6. S.Salahshour, G.A.Shekari, A.Hakimzadeh, A novel approach for ranking triangular intuitionistic fuzzy numbers, AWER Proedia Information Technology, 1(2012) , 442-446
7. S.Salahshour, S.Abbasbandy, T.Allahviranloo, Ranking fuzzy numbers using fuzzy maximizing-minimizing point, Advances in Intelligent systems Research, IFSA-EUSFLAT
2011.