International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 1708

ISSN 2229-5518

Smart Power Flow Control Through Distribution

Systems Utilizing Advanced Technique

Noha H. El-Amary, Mohamed El Fakharany, Yasser Galal Mostafa

Abstract— Smart electrical power flow control in distribution systems is targeted in this paper. Optimal electrical power continuity through energy management, self healing, high reliability and real-time pricing is one of the main aims of the researches. In this paper, a smart electrical power grid is represented to save the power flow continuity with minimum power losses in case of any abnormal condition. The optimum power continuity is achieved utilizing a developed Particle Swarm Optimization (PSO) technique. This technique is programmed to fulfill two main tasks. The first task is finding all the possible alternative paths for supplying the loads, in case of fault occur or abnormal condition. The second task is modifying the angles of the buses' voltages of the electrical power system to determine the optimal path with minimum power loss. The optimal determined path could have less power losses than that of the path already obtained by the initial power flow analysis. The buses' voltages angles can be modified using static VAR compensators, capacitor banks, or Flexible AC Transmission System devices (FACTs) technology. The performance of the developed technique is tested on a standard IEEE 14-bus system and the results are satisfied.

Index Terms— Energy management, minimum power loss, optimal path, optimum power continuity, Particle Swarm Optimization (PSO)

technique, power flow control, Smart Grid (SG).

——————————  ——————————

1 INTRODUCTION

smart grid can be defined in many ways, however, there is no agreement on a universal definition for it be- cause of the diverse range of factors, and numerous
competing taxonomies. Smart grid refers to a modernization of the electricity delivery system so it monitors, protects and automatically optimizes the operation of its interconnected elements (from the central and distributed generator through the high-voltage network and distribution system, to industri- al users and building automation systems, to energy storage installations and to end-use consumers and their thermostats, electric vehicles, appliances and other household devices). A smart grid delivers electricity from suppliers to consumers using digital technology to save energy, reduce cost and in- crease reliability and transparency. In brief, smart grid is the use of sensors, communications, computational ability and control in some form to enhance the overall functionality and reliability, and improve the efficiency and quality of the elec- tric power system [1].
A century ago, most industrialized countries built the electric power grid which has been growing ever since in its capacity and size. In the last few decades, the grid has been technologi- cally upgraded with automation and monitoring schemes, and new techniques has been implemented to modernize the grid. In the last two decades there was a high concentration on the integration of renewable energy sources into the grid in order to minimize environmental concerns [2]. The evolution of SG is traced to several innovations such as the installation of power system stabilizers, phase shifting transformers, FACT’s and Phasor Measurement Units (PMU’s) with the aim of achieving better control of the grid and minimizing power losses [3]. In the middle of the 1980’s, many electrical engi- neering researchers have paid a great attention to the applica- tion of PMU’s in power system monitoring and control.
PMU’s are high speed units distributed throughout a trans- mission network, which can obtain phasor measurements by synchronizing with each other through the Global Positioning Satellites (GPS). This network of PMU’s forms a Wide Area Monitoring System (WAMS) that can provide real-time moni- toring on a regional and national scale [4], [5].
Artificial Intelligence techniques play great role in dealing with the power system problems. The PSO technique is one of the ad- vanced and, nowadays, widely used optimization techniques that can be applied to many of power systems optimization problems.
PSO technique has many advantages such as [6]:
1) It has fewer parameters to adjust and so it is easier to imple-
ment.
2) It has a more effective memory capability since every particle
remembers its own previous best value as well as the neighbor-
hood best.
3) It is more efficient in maintaining the diversity of the swarm,
since all the particles use the information related to the most suc-
cessful particle in order to improve themselves.
4) It is not largely affected by the size and nonlinearity of the
problem and can converge to the optimal solution where most ana-
lytical methods fail to converge.
The PSO algorithm has been applied to a lot of engineering
problems with very promising results. Among the published litera-
ture, PSO has been used in electrical power engineering for [7]-[9]:
• Training neural networks for power transformer protection.
• Controlling voltage and Reactive Power in electric power
systems.
• Estimating states in practical distribution system.
• Solving the economic dispatch problem.
• Designing an optimum PID controller in AVR system.
• Designing a multi-machine power system stabilizer.
• Identifying dynamic security border.

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 1709

ISSN 2229-5518

This paper presents optimum power continuity through distribution systems by finding the possible alternative paths in case of the occurrence of a fault in the system, and also con- trol power flow in a smart way by changing the voltages’ an- gles of the buses to obtain the minimum power loss path new- ly developed PSO technique to achieve.

2 MATHEMATICAL MODELING

2.1 Power Flow

The power flow concept is explained on two-bus system and then generalized for the 14-bus IEEE Standard System.
Two buses of an electrical network with voltage phasors Vi∟δi and Vj∟δj are shown in Fig. 1. The two buses are con- nected through a transmission line with impedance Z = R + jX. The current phasor I∟β flows through the line from bus-i to bus-j (3).
Vi∟δi Vj∟δj

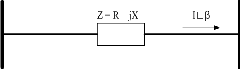
Bus-i Bus-j

Fig. 1. Simplified two-bus network

In power system analysis, some of the traditional system measured quantities are the real and reactive power injected to each bus (Pi, Qi) and the real and reactive power flow from bus-i to bus-j (Pij, Qij) which are calculated by the following equations:
Pi = Σ (Vi Vj Yij cos (δi-δj+θij)), for j = 1, 2… N (1) Qi = Σ (Vi Vj Yij sin (δi-δj+θij)), for j = 1, 2… N (2) Pij = Vi Vj Yij cos (δi-δj+θij) - Vi2 Yij cos (θij) (3) Qij = Vi Vj Yij sin (δi-δj+θij) - Vi2 (Yij sin (θij) + Bcapij) (4)
Where:

2.2 Power Loss

In electrical power systems there are always electrical power losses. These power losses are not desirable to be large in the system, as this will affect the overall quality of the pow- er delivered by the network and the reliability of the electrical system.
One of the main targets from the developed smart grid in this paper is minimizing the grid power losses and maximiz- ing the delivered power to the customers. This is the reason for considering the power loss control one of the major topics in power system research. It leads the researchers to continu-
ously search for new methods to reduce the power losses in the electrical network.
The basic rule of calculating power loss in the network transmission lines is
Ploss = I2R (5) Where:
Ploss : is the transmission line power loss
I: is the current flowing in the transmission line
R: is the resistance of the transmission line.
And it can be converted to the following form:
Ploss = (ΔV/Z)2 R (6) Where:
ΔV: is the voltage difference between any two consecutive connected buses.
ΔV= ((Vi cos(θi ) - Vj cos(θj ))2 + (Vi sin(θi ) - Vj sin(θj ))2)1/2
(7)

3 PARTICLE SWARM OPTIMIZATION

3.1 PSO Technique Objective

A newly developed PSO technique is programmed to opti- mize power flow in the electrical power system. It works on changing the values of the voltage angles of the buses to min- imize the power loss, to achieve better energy management through the electric grid and maintain power continuity.
PSO optimizes our problem by having a population of can- didate solutions which are the ten particles identified that are moving around in the search space according to the mathe- matical formula over the position and velocity of the particle. Each particle movement is influenced by its local best known position and is also guided toward the best known positions in the search-space, which are updated as better positions that are found by other particles. This leads the swarm to move toward the best solutions and hence obtain a global best solu- tion for the optimization problem.

3.2 PSO Equations

The concept of the particle swarm optimization technique is that it adjusts the velocity and location of each particle to- wards its personal best and global best locations as per the following equations:

VRfR = VRiR + cR1 RrR1R (XRpbestR - XRiR) + cR2 RrR2R(XRgbestR - XRiR) (8) XRf R= XRi R+ VRf R (9) where:

cR1R and cR2:R: are two positive constants called cognitive and social parameters respectively.

rR1R and rR2:R: are random numbers distributed between 0 and 1. VRfR and VRi R: are the final and initial velocities of the particle

during one iteration respectively.

XRf Rand XRi R: are the final and initial positions of the particle during one iteration respectively.

XRpbestR: is the particle personal best position. XRgbestR: is the particle global best position.

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 1710

ISSN 2229-5518

4 SIMULATION AND RESULTS

This work aims two main targets, which are; 1- searching all the alternative possible paths in case of faulted network, 2- then finding the optimal path and adjusting the value of its buses' voltage angles for optimizing the power flow to be with minimum power losses.
This work is developed through three stages, which are;
1- Simulating the power network on the Electrical Transient
Analysis Program (ETAP) to evaluate the power flow in nor-
mal healthy case and in faulted (unhealthy cases).
2- Developing a Matlab/m-file program, to find all the pos-
sible alternative paths for the power to feed the system dis-
connected parts due to the fault.
3- Developing a PSO technique program to find the optimal
path. The PSO program finds the optimum values of the bus-
es' voltage angles of the optimal path, for optimizing the pow-
er flow through minimizing its power loss. The PSO program is fed from the ETAP and the developed Matlab/m-file pro- grams to determine the available alternative paths.

The previous stages are illustrated in Fig. 2

4.1 AI Technique for Determination of Paths after a

Fault

1) Fault at a Bus

Figure 3 illustrates the circuit diagram of the standard IEEE
14-Bus system with fault occurrence at bus-6. The faulted bus
is circled by a dotted oval shape.

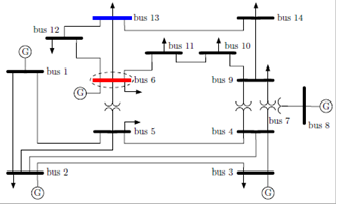
Fig. 3. IEEE 14-Bus system with fault at bus-6

Power system simulation and power flow studies using ETAP program

Determining all possible alternative power flow paths and their power losses in case of fault occurrence (utilizing a newly developed Matlab/m-file)

Optimization stage (utilizing PSO technique) for determining the optimal alternative power flow path and their voltage angles to fulfill minimum power loss

Optimal power flow path

After the occurrence of a fault at bus-6, there are only 18 paths which are available to feed the critical load at bus 13 as shown in Table I. The available paths consist of up to 8 buses at maximum which have voltage magnitudes and angles that will be entered as inputs to the PSO program.

TABLE 1

AVAILABLE PATHS AFTER FAULT OCCURRENCE AT BUS-6

Fig. 2. The three main stages of the developed work

The developed technique is applied to the IEEE 14- Bus standard system
In our research a scenario is proposed that there is a critical load at bus-13 which shall be fed continuously without inter- ruption, although any fault occurred in the system. In case (1), it is assumed that the fault occurred at one of the system’s buses which is bus-6. In case (2), the fault is assumed to be at one of the system’s branches which is the branch connecting bus-6 and bus-13. The total number of the available paths from the generation sources to the critical load is calculated after the occurrence of the fault in each case using a newly developed Matlab/m-file program.
The total number of paths that can feed the critical load at bus-13 from the different generation sources of the IEEE 14- Bus system are 63 paths without the occurrence of any fault in the system.

2) Fault at a Branch

The fault occurrence on the line connected bus-6 and bus-13 is shown in Fig. 4.

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 1711

ISSN 2229-5518

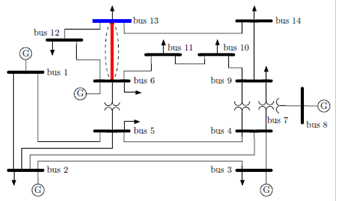
Fig. 4. IEEE 14-Bus system with fault at branch between bus-6 and bus-13

After the occurrence of a fault at the branch connecting bus-6 and bus-13, there are 43 paths available to feed the critical load at bus-13 as shown in Table 2.

TABLE 2

AVAILABLE PATHS AFTER FAULT OCCURRENCE AT THE BRANCH BETWEEN BUS-6 AND BUS-13

4.2 Initial Power Loss Calculation

The procedures of determining the alternative paths and cal- culating the initial power loss calculation, after a fault occur- rence, can be summarized in the flowchart shown in Fig. 5.
START

Enter the system parameters and data

Determine all the possible alternative paths for power flow in case of fault occurrence

Calculate ΔV and Ploss (between each two consecutive buses in the available alternative paths)

Calculate the total power losses of the path

Plt = Σ Ploss – path

= Σ I2 R =Σ (ΔV/Z)2 R

Identify the path of the minimum power losses

Pltmin = min (Plt)

END

IJSER © 2013 http://www.ijser.org

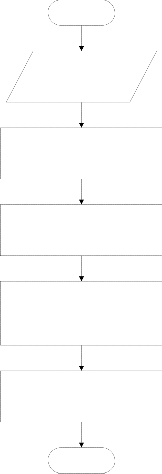
Fig. 5. Initial power loss calculation flowchart

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 1712

ISSN 2229-5518

The total power loss for each path is calculated for case (1) (IEEE 14-Bus system with a fault at bus-6). The power losses calculation results is shown in Table 3.

TABLE 3

INITIAL TOTAL POW ER LOSS RESULTS

11- Checking the END conditions (No. of iteration or Ploss- min )

Figure 6 shows the flowchart which summarizes the previ- ous steps of the developed PSO technique program. In study- ing case (1), where the fault is at Bus-6, the 18 available alter- native paths which can feed the critical load at Bus-13 are con- sidered. Each path consists of 8 buses at maximum, which leads to have swarm particles with 8x18 variables at maxi- mum. The developed PSO technique is composed of 10 parti- cles.

START

Read the system data, parameters, load flow, and paths from both ETAP

and developed m-file

The calculation shows that the minimum power loss (Plt- min) is equal to 0.3662. It occurs in the third path passing through buses-1-2-4-9-14-13.

0 < Con < 90 No

θn+1 = θn – 0.15 – P*0.02

Yes

4.3 PSO Technique

The algorithm procedures and the flowchart of the PSO pro- gram are based on the assumption that voltage magnitudes are constants. The used technique changes only the values of the angles of the buses aiming to find the optimal alternative path that could deliver power with the lowest power loss value in this case. The algorithm procedures can be summarized in the

Calculate ΔV, CF (Ploss )

and determine θgbest

CF < Ploss(min)

or

i > I No

Yes

following steps;
1- Entering the network parameters, initial values and re-
sults after running the load flow program (ETAP pro-
gram) considering the fault.
2- Determining the available paths and the number of variables (using m-files).
3- Initialization of particles positions and velocities.
4- Checking that the condition of the angles is satisfied.
5- Calculating ΔV and Ploss.
6- Calculating the Cost Function (CF) and initializing
θgbest.
7- Applying PSO technique concept using (8) and (9).
8- Checking the constraint (Δθ).
Δθ = I θn+1 - θn I
0 < Δθ < 90°
9- Calculating the minimization function (CF) using (6)
and (7).

Calculate particles’ positions and

velocities

0 < Con < 90 No

Yes

Calculate ΔV, CF (Ploss )

Determine θpbest and θgbest

θn+1 = θn – 0.15 – P*0.02

θ = θgbest

END

10- Determining θpbest and θgbest .

Fig. 6. PSO technique flowchart

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 1713

ISSN 2229-5518

The particle swarm personal best “θpbest ” for the 10 particles are calculated, from which the global best “θ gbest ” is obtained, as shown in Table 4. The initial values of the angles of the first path are changed as shown in the schedule illustrated in Table 5.

TABLE 4

RESULTS OF ΘPBEST AND ΘGBEST

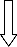
The personal best solution “θpbest” for the 10 particles are
calculated from which the global best “θgbest” is also obtained.
The initial values of the angles of the first path are changed
as shown in the following schedule.

TABLE 5

GBEST AND INITIAL VALUES OF THE SELECTED BUSES ANGLES

The lowest Power Loss (Plossmin ) occurred on particle (1) with a value equals to 0.1163.
These new voltage angles leads to reduce the power losses of the system from 0.3662 to 0.1163 as clarified in Table 7. They lead to have another alternative path of a lower power loss which is the path passing through the buses 1-2-3-4-9-14-13.

TABLE 7

RESULTS COMPARISON OF POW ER LOSS

5 CONCLUSION

4.4 Power Losses Results

Each Particle carries the 18 paths. The minimum power loss that can be obtained in each particle is shown in Table 6.

TABLE 6

FINAL TOTAL POWER LOSS RESULTS

Particle Total Power Loss

This paper presents an intelligent smart grid which can achieve optimum power continuity and smart power flow control through distribution systems during any abnormal conditions.
This research targets to find all the alternative possible paths in case of faulted network, then adjust the values of the paths buses voltages angles for optimizing the power flow to be with minimum power losses. The work is developed through three stages, which are; 1- Simulating the power net- work on the ETAP simulation program to evaluate the power flow in normal healthy case and in abnormal conditions (faulted unhealthy cases). 2- Developing a Matlab/m-file pro- gram, to find all the possible alternative paths for the power to feed the system disconnected parts during the fault. 3- Devel- oping a PSO technique program to find the optimal path. The PSO program finds the optimum values of the buses' voltage

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013 1714

ISSN 2229-5518

angles of the optimal path, for optimizing the power flow through minimizing its power loss. The PSO program is fed from the ETAP and the developed Matlab/m-file programs to determine the available alternative paths. The optimal deter- mined path may have less power losses than that of the path already obtained by the initial power flow analysis.
The new developed PSO technique succeeds in finding an available alternative power flow path and adjusting its buses voltages angles to be with minimum power loss in case of fault occurrence. The newly technique is applied to a standard IEEE 14-Bus system. The results illustrate that this technique can be used to achieve the power flow continuity and optimi- zation.

REFERENCES

[1] Clark W. Gellings, "The Smart Grid: Enabling Energy Efficiency And

Demand Response", The Fairmont Press, April 20, 2011.

[2] M. Godoy Simões, R. Roche, E. Kyriakides, A. Miraoui, B. Blunier, K.

McBee, S. Suryanarayanan, P Nguyen and P. Ribeiro “Smart-Grid

Technologies and Progress in Europe and the USA”, IEEE Energy

Conversion Congress and Exposition (ECCE), September 17, 2011.

[3] T. J. Overbye, J. D. Weber, “Visualizing the electric grid”, IEEE Spec- trum, vol. 38, no. 2, pp. 52-58, 2000.

[4] S. M. Amin, “For the good of the grid”, IEEE Power and Energy

Magazine, vol. 6, no. 6, pp. 48-59, Oct. 2008.

[5] S. Chakrabarti, E. Kyriakides, and D. G. Eliades, “Placement of syn-

chronized measurements for power system observability,” IEEE

Transactions on Power Delivery, vol. 24, no. 1, pp. 12-19, Jan. 2009.

[6] Yasser G. Mostafa, M. Sayed Hussien, and N. H. El-Amary, "Co- ordination of Overcurrent Voltage Controlled Protection in Large Electrical Networks using Particle Swarm Optimization Technique", Proceeding of IEEE Conference, the 2009 International Conference on Computer Engineering and Systems, ICCES' 09, Cairo, Egypt, 14th –

16th December, 2009.

[7] Yamille del Valle, Ganesh Kumar Venayagamoorthy, Salman Mo-

hagheghi, Jean-Carlos Hernandez, Ronald G. Harley, "Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems", IEEE Transactions on Evolutionary Computation, Vol. 12, No. 2, April 2008.

[8] Y. Fukuyama, and H. Yoshida, "A Particle Swarm Optimization for

Reactive Power and Voltage Control in Electric Power Systems", Evo- lutionary Computation Congress, Vol. 1, pp. 87-93, 2001.

[9] S. Naka, T. Genji, T. Yura, and Y. Fukuyama, "A Hybrid Particle Swarm Optimization for Distribution State Estimation", IEEE Trans- actions on Power Systems, Vol. 18, No. 1, pp. 60-68, February 2003.

[10] A. S Kannan, and R. Kayalvizhi, "Utility of PSO for Loss Minimiza- tion and Enhancement of Voltage Profile Using UPFC", International Journal of Scientific and Engineering Research, Vol. 2, No. 2, Febru- ary 2011.

[11] U.S. Department of Energy, "Smart Grid System Report”, July 2009.

[12] Brown, R.E.,"Impact of Smart Grid on Distribution System Design",

IEEE, Power and Energy Society General Meeting – Conversion &

Delivery of Electrical Energy in the 21st Century, 24 July 2008.

[13] Chuck Goldman, Roger Levy, “Smart Grid Technical Advisory Pro-

ject”, Lawrence Berkeley National Laboratory, February 2010.

[14] John J. Grainger and William D. Stevenson, “Power System Analy-

sis,” McGraw-Hill, International Editions 1994.

[15] Hadi Saadat, “Power System Analysis,” Second Edition, Internation- al Edition 2004.

IJSER © 2013 http://www.ijser.org