International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

Sequential Division Circuit Using Reversible Logic Gates

Md. Ashraful Haque Department of Electrical and Electronic Engineering

Islamic University of Technology, Board Bazar, Gazipur-1704, Bangladesh. limon_786@yahoo.com

Sadia Rahman Department of Applied Physics Electronics and Communication Engineering

Dhaka University. sadia445514@yahoo.com

Abstract:

Quantum computer is a computation device that incorporates quantum mechanical phenomena
distinctively to perform operation on data in terms of superposition & entanglement. In contrast to traditional computer where data is represented by means of bits, Q.C makes use of Quantum bits
(qubits)for data representation [12]. There are several reasons that researchers are working so hard to
develop a practical quantum computer. First, atoms change energy states very quickly -- much more quickly than even the fastest computer processors. Next, given the right type of problem, each qubit can take the place of an entire processor -- meaning that 1,000 ions of say, barium, could take the place of a
1,000-processor computer. The key is finding the sort of problem a quantum computer is able to solve.

Keywords: Reversible logic gate, quantum bits, MUX, Sequential Circuits.

Introduction

Quantum computation and quantum information
is the study of the information processing tasks that can be accomplished using quantum
mechanical systems. The basic principle behind quantum computation is that quantum properties
can be used to represent data and perform operations on these data [1].Quantum computer is a computation device that incorporates
quantum mechanical phenomena distinctively to perform operation on data in terms of
superposition & entanglement. In contrast to traditional computer where data is represented by means of bits, Q.C makes use of qubits for
data representation [2]. There are several reasons that researchers are working so hard to develop a
practical quantum computer. First, atoms change energy states very quickly -- much more quickly
than even the fastest computer processors. Next, given the right type of problem, each qubit can take the place of an entire processor -- meaning
that 1,000 ions of say, barium, could take the place of a 1,000-processor computer. The key is
finding the sort of problem a quantum computer is able to solve.
If one were to be built today, no information on the Internet would be safe. Our current methods of encryption are simple compared to the complicated methods possible in quantum computers. Quantum computers could also be used to search large databases in a fraction of the time that it would take a conventional computer. It has been shown in theory that a quantum computer will be able to perform any task that a classical computer can. However, this does not necessarily mean that a quantum computer will outperform a classical computer for all types of task. If we use our classical algorithms on a quantum computer, it will simply perform the calculation in a similar manner to a classical computer. In order for a quantum computer to show its superiority it needs to use new algorithms which can exploit the phenomenon of quantum parallelism.Quantum mechanics incorporates four classes of phenomena for which classical physics cannot account:
 The quantization of certain physical properties
 wave-particle duality

International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

902

 The uncertainty principle
 quantum entanglement [3]
The bit (each bit represents either a one or a zero) is the fundamental concept of classical computation and classical information. The elementary unit of quantum information is the
qubit. A single qubit can represent a │1⧽, a│0⧽,
or, crucially, any quantum superposition of
these. A quantum computer with n qubits can be in an arbitrary superposition of up to 2n different states simultaneously. For our purposes, the
most general model of the qubit is:

|ψ⧽ =α | 0 ⧽ +β |1⧽

Where α and β are complex numbers such that
|�|2+|�|2 =1

Advantages of Reversible logic:

• Landauer has shown that for irreversible logic computations, each bit of information lost, generates kTlog2 joules of heat
• Bennett showed that kTln2 energy dissipation would not occur, if a computation were carried out in a reversible way
• Whenever a logic operation is performed, the computer erases information. All these logic operations are irreversible dissipating a lot of heat.
• The current irreversible technologies will dissipate a lot of heat and can reduce the life of the circuit.
• As Moore’s law continues to hold, processing power doubles every 18 months.
• Reversible logic operations do not erase (lose) information and dissipate much less heat.
Reversible logic is likely to be in demand in high speed power aware circuits.

THE QUANTUM CIRCUIT MODEL:

Reversible circuits form the basic building blocks of quantum computers, as all quantum operations are reversible. Quantum circuitry consists of sequence of quantum gates applied to Quantum register having size n is made up with combination of uniquely addressable qubits having individual couplings. Each quantum gate carries reversible property which incorporates transformation by means of unitary operator between the inputs and outputs. Hence quantum circuit can be defined in terms of Quantum register to which a finite no. of quantum operations are applied

REVERSIBLE EQVIVALENT GATES USED FOR DESIGNING SEQUENTIAL CIRCUITS:

 NOT gate (Pauli-X gate):

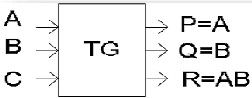
 Toffoli gate:

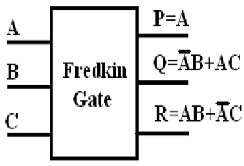
 Fredkin Gate:

International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

903

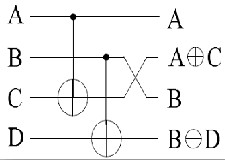
 HNFG gate:

 Modified TSG (MTSG)

gate:

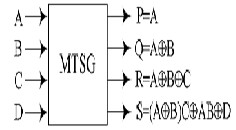
 Controlled-NOT gate

(Feynman gate):

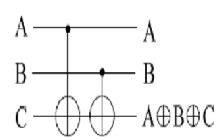
 Feynman double gate:

 TS-3 Gate:

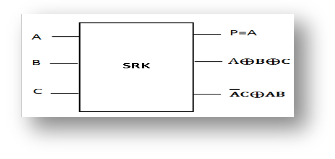
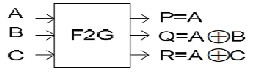
 SRK Gate:

Components of Division Circuit:

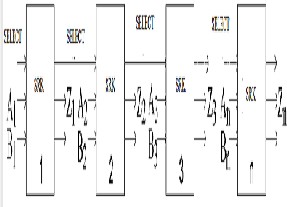
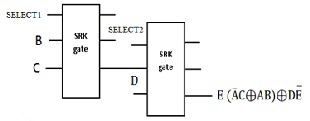
 2 input n bit reversible MUX :

International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

904

 3 input n bit reversible MUX:

Basic cell for 3 input MUX

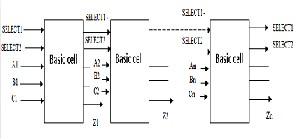
 n-bit reversible PIPO left-shift registers:

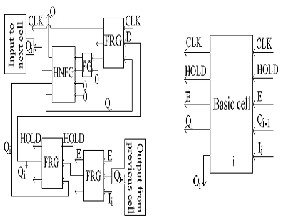
Basic cell for the reversible PIPO left-shift register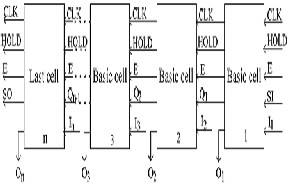

An n-bit reversible PIPO left-shift registers
 n bit parallel Subtractor: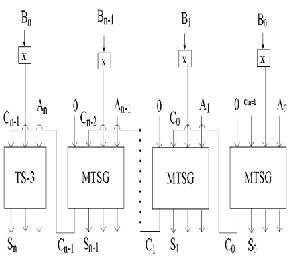

 Control Circuit: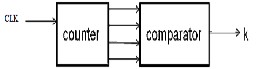

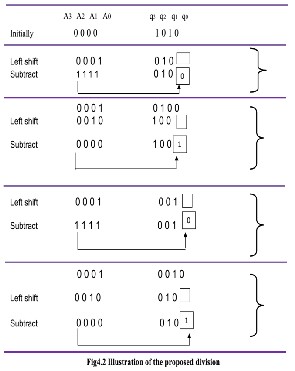
Reversible Divider:

The following figure shows the reversible design of non performing restoring division circuit for positive integers. This circuit includes

 two n bit reversible PIPO left- shift register

 one 3input n bit reversible MUX

International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

905

 one 2i input n bit reversible MUX and
 One n bit reversible parallel subtractor for performing subtraction.
When the division operation is completed,
register
 Q (qn-1qn-2…q0) contains the quotient and
 A (an-1an-2…a0) contains the remainder.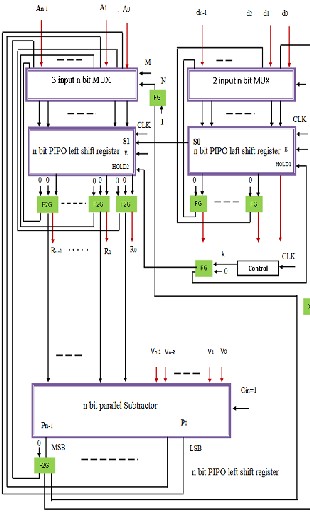

Fig: reversible divider

Circuit Operation:

Initially:
A (an-1an-2…a0) =0
D (dn-1dn-2…d0) = dividend, V (vn-1vn-2…v0) = divisor

K = 0

If M = 1, and N=1then 3-input n bit MUX selects A (an-1an-2…a0) = 0, and when SELECT1=1, 2input n-bit MUX selects dividend D (dn-1dn-2…d0). During the clock pulse when E = 1 and HOLD2 = 0, the output data from 3input n-bit MUX are loaded into A, and when HOLD1 = 0, outputs from n-bit MUX are loaded into Q in parallel. When
E = 0, both A and Q act as left-shift registers. Then subtraction is performed using n-bit
reversible parallel subtract or.
If Pn-1=1, then N becomes 0 and if M=0 then 3 input n bit MUX selects B (bn-1, bn-2…..n0) (output of the shift register) and when SELECT=0 2 input n bit MUX selects data from

the quotient shift register. 𝑃n-1=0 is loaded into
q0 bit position of register Q and output data
from 3 input MUX is loaded into A during next clock pulse.
If Pn-1=0, then N becomes 1 and if M=0 then 3 input n bit MUX selects output of the n bit parallel subtract or and when SELECT=0 2 input MUX selects data from the quotient shift

register. 𝑃n-1=1 is loaded into q0 bit position of
register Q and output data from 3 input MUX is
loaded into A during next clock pulse.
It requires 2n+1 clock pulses to store the value of quotient into register Q. After 2n+1 clock pulses, Control outputs a high signal K. This signal is connected to HOLD1, input of Q register and HOLD2, input of A register. Thus Q stores the quotient and A stores the remainder indefinitely.

International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

906

Step- 6:

Inputs: A (an-1an-2…a0) =0 and D (dn-
1dn-2…d0) = dividend) are loaded
into A and Q register respectively

Step 7:

Step -8:

else
if SELECT = 0, M=0, N=1

Step -9:

Outputs from parallel subtract or and quotient left shift register are loaded
into A and Q registers respectively

Step-10:

else

Step-11:

SELECT = 0, M=0, N=0
After the division operation,
1qn-2…q0) = 0101 and
(an-1an-2…a0) = 0000

Algorithm:

Quotient Q (qn- Remainder: A

Step-12:

Outputs from remainder shift register and quotient left shift register are
loaded A and Q registers respectively.

[End if-else] Step -13:

count = count +1

Step-14:

E = 0

Step -15:

if (count = 2n+1)

Step-16:

break;

Inputs A (an-1an-2…a0) =0

D (dn-1dn-2…d0) = dividend and
V (vn-1vn-2…v0) = divisor

Outputs: Q (qn-1qn-2…q0) = quotient and

A (an-1an-2…a0) =remainder

Division Algorithm

Step -1:

K = 0,

Step -2:

SELECT = 1, M=1, N=1

Step -3:

E = 1

Step-4:

Count = 0

Step -5:

If CLK is high

Step-17:

else

Step-18:

if (CLK is high)

Step-19:

Occurrence of left shift of A and Q
register

Step-20:

Occurrence of subtraction
[End if-else]

Step-21:

if Pn-1=0( the MSB of sum)

Step-22:

. q0 will be 1 during the next CLK

Step-23:

3input MUX will select output from parallel subtractor

Step-24:

else

Step-25:

International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

907

q0 will be 0 during the next CLK

Step-26:

3 inputs MUX will select output from remainder shift register
[End if-else]

Step-27:

if ( count = 2n+1)

Step-28:

K = 1, HOLD1 and HOLD2 will be 1,

Step-29:

A and Q register will store remainder an
quotient indefinitely

[End if-else]

Table: Characteristics of the n-bit reversible divider.

Compone nts of reversible divider	Rever sible gates	Garbag e output	Const ant inputs	Quan tum cost
n bit reversible PIPO shift register	10n	6n+6	3n	36n
2-input n bit reversible MUX	n	n	0	5n
3-input n- bit reversible MUX	2n	2n	0	10n
n bit adder	n	2n	n-1	6n-4
NOT gate	n+1	0	0	0
Feynman gate and double Feynman	2n+2	1	3n+3	3n+3
Total	18n+3	10n+7	7n+2	60n- 1

Thus, an n-bit reversible division circuit can be realized by at least
10n+n+2n+n+n+1+2n+2=18n+3 gates and
6n+6 + n + 2n+2n+1= 10n+7 garbage outputs with
36n+5n+10n+6n-4+3n+3 =60n-1 quantum cost

Conclusion:

 2-input n bit reversible MUX, requiring n gates, n garbage outputs and 5n quantum cost
 3-input n-bit reversible MUX, requiring
2n gates, 2n garbage outputs and 10n
quantum cost
 n bit reversible PIPO shift register, requiring 5n gates, 3n+3 garbage outputs and 18n quantum cost
 n+1 Feynman gates and (n+1) double Feynman gates to avoid fan-out and to invert input bit, requiring
(3n+3)quantum cost ,1 garbage output
 n-1 DKG gates, one TS-3 and (n-1) FG gate for n bit adder, requiring 2n-1 gates, 2n+2 garbage outputs and 7n-1 quantum cost
One NOT gate which has no quantum cost.

References

1. M.Nielsen and I.Chuang, Quantum computation and quantum information (Cambridge University Press,
Cambridge, UK 2000).]
2. [12] Quantum computation.David
Deutsch,physics world,1/6/92
3. P.A.M Dirac, The principles of quantum
Mechanics,Claredon Press, Oxford,1930
4. Simon, D.R. (1994). "On the power of quantum computation". Foundations of Computer Science, 1994 Proceedings,
35th Annual Symposium on: 116–123.
5. Mahmudul Hasan, Raqibul Hasan, Masud Hasan, Asif Islam Khan
‘QUANTUM NETWORKS FOR
BOOTH’S AND MODIFIED BOOTH’S ALGORITHM FOR BINARY MULTIPLICATION’
6. Landauer, R, “Irreversibility and Heat Generation in the Computing Process”, IBM J. Research and Development, vol. 3, pp.
183-191,July 1961.

International Journal of Scientific & Engineering Research, Volume 6, Issue 4, April-2015

ISSN 2229-5518

908

7.Noor Muhammed Nayeem, Md. Adnan Hossain, Md. Mutasimul Haque, Lafifa Jamal, Hafiz M. Hasan Babu “Novel Reversible Division Hardware”IEEE
8. Vlatko Vedral, Adriano Bareno and Artur Ekert, “Quantum Networks for Elementary Arithmetic Operations”, arXiv:quantph/
9511018 v1, nov 1995.
9. J. Smoline and D. P. DiVincenzo, “Five two-qubit gates are sufficient to implement the quantum Fredkin gate,” Physical Review A, vol. 53, no. 4, pp. 2855-2856, 1996.
10.Himanshu Thapliyal and M.B Srinivas, “A Beginning in the Reversible Logic Synthesis of Sequential Circuits.”
11. H. Thapliyal, S. Kotiyal, and M. B. Srinivas, “Novel BCD Adders and Their Reversible Logic Implementation for IEEE
754r Format,” Proceedings of 19th International Conference on VLSI Design, pp.387-392, January 03-07, 2006.
12.Krishnaveni, D, Geetha Priya, M, “A Novel Design of Reversible Universal Shift Register with Reduced Delay and Quantum Cost”, Submitted for Review to VLSI Systems Journal, IEEE
13. Kihwan Jun, B.S.E.E. M.S.E.E
‘Modified Non-restoring Division
Algorithm with Improved Delay Profile’