International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 1
ISSN 2229-5518
G.Vaithiyanathan1,6, K.Venkatesan2,6, S.Sivaramakrishnan3,6, S.Siva4,6 and S. Jayakumar5
Abstract -In a typical processor, Multiplication is one of the basic arithmetic operations and it requires subst antially more hardware resources and processing time than addition and subtraction. In fact, 8.72% of all the instruction in typical processing units is multipliers. In com puters, a typical central processing unit devot es a considerable am ount of processing time in implem enting arithmetic operations, particularly multiplication
operations .In this project , the comparative study of different multipliers is done for low power requirem ent and high speed, also gives information of
“Urdhva Tiryakbhyam” algorithm of Ancient Indian Vedic Mat hem atics which is utilized for multiplication to improve the speed, area param et ers of multipliers. Vedic Mathem atics also suggests one m ore form ulae for m ultiplication i.e. “Nikhilam Sutra” which can increase the speed of multiplier by reducing the num ber of iterations. W hich increase the speed of the multiplier as well as processor or system .
Index Terms- Delay, Multiplier, Nikhilam, Speed , Urdhvatiryakbhyam, Vertical and Crosswise, Vedic Multiplication.
—————————— ——————————
Multiplication is an important fundamental function in arithmetic operations. Multiplication-based operations such as Multiply and Accumulate (MAC) and inner product are among some of the frequently used Computation- Intensive Arithmetic Functions (CIAF) currently implemented in many Digital Signal Processing (DSP) applications such as convolution, Fast Fourier Transform (FFT), filtering and in microprocessors in its arithmetic and logic unit. For multiplication algorithms performed in DSP applications latency and throughput are the two major concerns from delay perspective. Nikhilam Sutra is then discussed and is shown to be much more efficient in the multiplication of large numbers as it reduces the multiplication of two large numbers to that of two smaller ones. This Sutra also shows the effectiveness of to reduce the NXN multiplier structure into an efficient 4X4 multiplier structures. The Multiplier Architecture is based on the Vertical and Crosswise algorithm of ancient Indian Vedic Mathematics[5]
——————————
1.G.Vaithiyanathan, vaithi24.eie@gmail.com
2.K.Venkatesan, venkatesan92.eie@gmail.com
3.S.Sivaramakrishnan, shivaglitzzz@gmail.com
4.S.Siva, sivaac09uei085@gmail.com
5. S.Jayakumar, Ph.D Research Scholar & Asst.Lecturer of
![]()
Adhiyamaan College of Engineering, Hosur. jayakmr@gmail.com
6.Dept. of Electronics and Instrumentation, Student of Adhiyamaan
College of Engineering, Hosur
The proposed Vedic multiplier is based on the Vedic multiplication formulae (Sutras). These Sutras have been traditionally used for the multiplication of two numbers in the decimal number system. In this work, the same ideas to the binary number system to make the proposed algorithm compatible with the digital hardware. Vedic multiplication based on some algorithms, some are discussed below
The multiplier is based on an algorithm Urdhva Tiryakbhyam (Vertical & Crosswise) of ancient Indian Vedic Mathematics. Urdhva Tiryakbhyam Sutra is a general multiplication formula applicable to all cases of multiplication. It literally means “Vertically and crosswise”. It is based on a novel concept through which the generation of all partial products can be done with the concurrent addition of these partial products. Power dissipation which results in higher device operating temperatures. Therefore it is time, space and power efficient. It is demonstrated that this architecture is quite efficient in terms of silicon area/speed [10, 4].
IJSER © 2013
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 2
ISSN 2229-5518
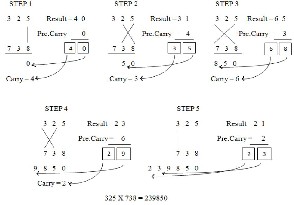
Figure 1: Multiplication of two numbers
To illustrate this multiplication scheme, for example, the multiplication of two decimal numbers (325 *
738). Line diagram for the multiplication is shown in Fig.2.
The digits on the both sides of the line are multiplied and added with the carry from the previous step. This generates one of the bits of the result and a carry. This carry is added in the next step and hence the process goes on. To make the methodology more clear, an alternate illustration is given with the help of line diagrams in figure.4 where the dots represent bit „0‟ or „1‟[4].
Multiplicand X3 X2 X1 X0
Multiplier Y3 Y2 Y1 Y0
--------------------------------------------------------- Product H G F E D C B A
P7 P6 P5 P4 P3 P2 P1 P0
----------------------------------------------------------
2) Algorithm for 8 X 8 Bit Multiplication Using Urdhva Triyakbhyam (Vertically and crosswise) for two Binary numbers [11]
A = A7 A6 A5 A4 A3 A2 A1 A0
X1 X0
B = B7 B6 B5 B4 B3 B2 B1 B0
Y1 Y0
X1 X0
* Y1 Y0
------------------------------------- F E D C
CP = X0 * Y0 = C
CP = X1 * Y0 + X0 * Y1 = D CP = X1 * Y1 = E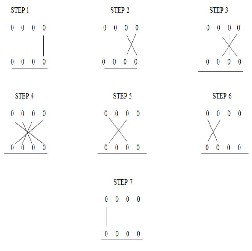
To illustrate the multiplication algorithm, let us consider the multiplication of two binary numbers a3a2a1a0 and b3b2b1b0. As the result of this multiplication would be more than 4 bits, we express it as... r3r2r1r0. Line diagram for multiplication of two 4-bit numbers is shown in Fig. 4 which is nothing but the mapping of the Fig.5 in binary system. For the simplicity, each bit is represented by a circle. Least significant bit r0 is obtained by multiplying the least significant bits of the multiplicand and the multiplier. The process is followed according to the steps shown in Fig. 5
Figure 2: Line diagram for multiplication of two 4
- bit numbers
Firstly, least significant bits are multiplied which gives the least significant bit of the product (vertical). Then, the LSB of the multiplicand is multiplied with the next higher bit of the multiplier and added with the product of LSB of multiplier and next higher bit of the multiplicand (crosswise). The sum gives second bit of the product and the carry is added in the output of next stage sum obtained by the crosswise and vertical multiplication and addition of three bits of the two numbers from least significant position..
For example, if in some intermediate step, we get 110, then 0
IJSER © 2013
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 3
ISSN 2229-5518
will act as result bit (referred as rn) and 11 as the carry (referred as cn). It should be clearly noted that cn may be a multi-bit number.Thus we get the following expressions:
r0=a0b0…… (1)
c1r1=a1b0+a0b1…… (2)
c2r2=c1+a2b0+a1b1 + a0b2 (3)
c3r3=c2+a3b0+a2b1 + a1b2 + a0b3 (4)
c4r4=c3+a3b1+a2b2 + a1b3…… (5)
time taken by the carry to propagate through the adders which form the multiplication array.
Nikhilam Sutra literally means “all from 9 and last from 10”. Although it is applicable to all cases of multiplication, it is more efficient when the numbers involved are large. Since it finds out the compliment of the large number from its nearest base to perform the multiplication operation on it, larger is the original number,
lesser the complexity of the multiplication. We first illustrate
c5r5=c4+a3b2+a2b3
c6r6=c5+a3b3
(6)
(7)
this Sutra by considering the multiplication of two decimal numbers (96 * 93) where the chosen base is 100 which is nearest to and greater than both these two numbers.
With c6r6r5r4r3r2r1r0 being the final product. Hence this is the general mathematical formula applicable to all cases of multiplication.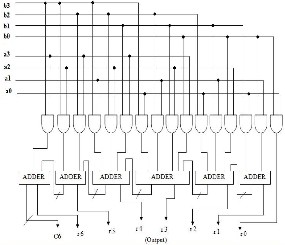
Figure 3: Architecture of the Urdhva tiryakbhyam multiplier
This hardware design is very similar to that of the famous array multiplier where an array of adders is required to arrive at the final product. All the partial products are calculated in parallel and the delay associated is mainly the
Figure 4: Multiplication Using Nikhilam Sutra
The right hand side (RHS) of the product can be obtained by simply multiplying the numbers of the Column
2 (7*4 = 28). The left hand side (LHS) of the product can be
found by cross subtracting the second number of Column 2 from the first number of 12 Column 1 or vice versa, i.e., 96 - 7
= 89 or 93 - 4 = 89. The final result is obtained by concatenating RHS and LHS (Answer = 8928) [4].
Vedic multiplier is faster than array multiplier and Booth multiplier. As the number of bits increases from 8x8 bits to 16x16 bits, the timing delay is greatly reduced for Vedic multiplier as compared to other multipliers. Vedic multiplier has the greatest advantage as compared to other multipliers over gate delays and regularity of structures. Delay in Vedic multiplier for 16 x 16 bit number is 32 ns
while the delay in Booth and Array multiplier are 37 ns and
IJSER © 2013
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 4
ISSN 2229-5518
43 ns respectively [12]. Thus this multiplier shows the highest speed among conventional multipliers. It has this advantage than others to prefer a best multiplier.
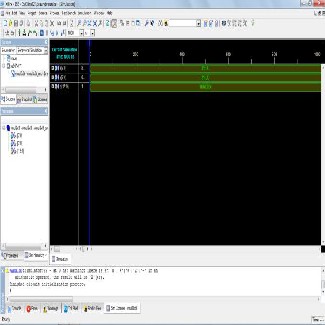
Figure 5: Result
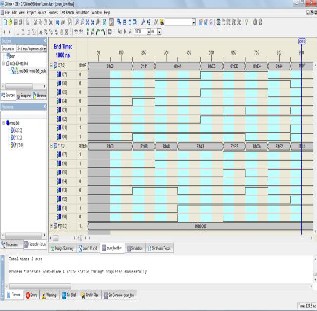
Figure 6: I/O Vedic Multiplication Algorithm
Description:
a : Input data 8 – bit b : Input data 8 – bit
q _ out : Output data 16 – bit
a = 11110000 b = 10101010
q = 1001111101100000.
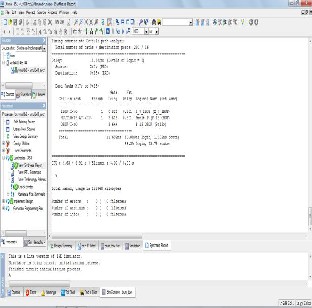
Figure 7: Report for Vedic Multiplier
Architecture of Vedic multiplier based on speed specification is designed here for following criteria
Increase the Speed of the system
To acquire good efficiency of the system
Reduce the time delay as well as path delay in the multiplier
The combinational path delay of Vedic multiplier obtained after compared with normal multipliers and found that the proposed Vedic multiplier.
It can be concluded that Vedic Multiplier is superior in all respect like speed, delay, complexity.
However Array Multiplier requires more power
IJSER © 2013
International Journal of Scientific & Engineering Research Volume 4, Issue 1, January-2013 5
ISSN 2229-5518
consumption and gives optimum number of components required. Ancient Indian Vedic Mathematics gives efficient algorithms orformulae for multiplication which increase the speed of devices. Urdhva Tiryakbhyam, is general mathematical formula and equally works the best. applicable to all cases of multiplication. Also, the architecture based on this sutra is seen to be similar to the popular array multiplier where an array of adders is required to arrive at the final product.
Vedic Mathematics, developed about 2500 years ago, gives us a clue of symmetric computation. Vedic mathematics deals with various topics of mathematics such as basic arithmetic, geometry, trigonometry, calculus etc. All these methods are very efficient as far as manual calculations are concerned. If all those methods effectively implement hardware, it will reduce the computational speed drastically. Therefore, it could be possible to implement a complete ALU using all these methods using Vedic mathematics methods. Vedic mathematics is long been known but has not been implemented in the DSP and ADSP processors employing large number of multiplications in calculating the various transforms like FFTs and control applications such as P, PI, PID Controller implementing in FPGA etc.
[1]. Implementation of Vedic Multiplier for Digital Signal Processing, International Conference on VLSI, Communication & Instrumentation (ICVCI) 2011, Proceedings published by International Journal of Computer Applications® (IJCA).
[2]. Gianluca Cornett a and Jordi Cortadella ―Asynchronous
Multipliers with Variable-Delay Counters, IEEE Conference, 2001, pp. 701-705.
[3]. Kiwon Choi and Mi nkyu Song, ―Design of a High Performance
32x32-Bit Multiplier With a Novel Sign Select Booth Encoder, IEEE Conference, 2001, pp. 701-704.
[4]. Wen-Chang Yeh and Chein-Wei Jen, ―High-Speed Booth
Encoded Parallel Multiplier Design, IEEE Transactions on
Computers, Vol. 49, No. 7, JULY 2000, pp. 692-701.
[5]. Jung-Yup Kang, Member, IEEE, and Jean-Luc Gaudiot, ―A
Simple High-Speed Multiplier Design, IEEE Transactions on
Computers, Vol. 55, No. 10, October 2006, pp.1253-1258.
[7]. Shiann-Rong Kuang, Jiun-Ping Wang, and Cang- Yuan Guo,
―Modified Booth Multipliers With a Regular Partial Product Array,‖ IEEE Transactions On Circuits And Systems—II: Express Briefs, Vol. 56, No. 5, May 2009, pp.404-408. Acknowledgement
It is a great opportunity to expresses our gratitude and sincere thanks to our Head of the Department Mrs.S.Sujatha for providing a proper encouragement to carry out this research work successfully.
IJSER © 2013