International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1884
ISSN 2229-5518
Routing Based Ant Colony Optimization in
Wireless Sensor Networks
ANJALI1, Navpreet Kaur2
ABSTRACT--W ireless Sensor Networks (W SN’s) have become an important and challenging research area in last year. W ireless Sensor Networks consisting of nodes with limited power are deployed to gather useful information from the field. In W SNs it is critical to collect the information in an energy efficient manner. Ant Colony Optimization, a swarm intelligence based optimization technique, is widely used in networ k routing. In this paper, we introduce a heuristic way to reduce energy consumption in W SNs routing process using Ant Colony Optimization. W e introduce three Ant Colony Optimization algorithms, the Ant System, Ant Colony System and improved AS and their application in W SN routing process. The simulation results show that ACO is an effective way to reduce energy consumption and maximize W SN lifetime.
Index Terms :-Ant colony optimization , Delay , Energy consumption, Routing , Routing protocols , Sensors , W ireless sensor networks.
![]()
Due to advance information technology, Wireless sensor networks (WSN’s) are rapidly developing area in both research and application. Wireless sensors have the ability to perform simple calculations and communicate in a small area. Wireless sensor networks have critical applications in the scientific, medical, commercial, and military domains. Although WSNs are used in many applications, they have several restrictions including limited energy supply and limited computation and communication abilities. These limitations should be considered when designing protocols for WSNs. Because of these considerations specific to WSNs, many routing schemes using end-to-end devices and MANETs [3] are inappropriate for WSNs. In sensor networks, minimization of energy consumption is considered a major performance criterion to provide maximum network lifetime. When considering energy conservation, routing protocols should also be designed to achieve fault tolerance in communications. In addition, since channel bandwidth is limited, protocols should have capability of performing local collaboration to reduce bandwidth requirements [4].
Anjali is currently pursuing masters degree program in electronic &
communication engineering in Lovely Professional University, India , PH-
9878001786. E-mail: anjalisehgal1988@mail.com
Navpreet Kaur is an Assist Professor in Lovely Professional University,
India, PH-8968699806. E-mail: Navpreet.kaur@lpu.co.in.
The basic method to transfer information from a sensor node to the base is called flooding. The optimization of network parameters for WSN routing process to provide maximum service life of the network can be regarded as a combinatorial optimization problem. Many researchers have recently studied the collective behavior of biological species such as ants as an analogy providing a natural model for combinatorial optimization problems. Ants in a colony are able to converge on the shortest among multiple paths connecting their nest and a food source. The driving force behind this behavior is the use of a volatile chemical substance called pheromone. While locating food, ants lay pheromone on the ground, and they also go in the direction where the concentration of pheromone is higher. This mechanism allows them to mark paths and subsequently guide other ants, and let good paths arise from the overall behavior of the colony.
The main goal of our study was to maintain network life time at a maximum, while discovering the shortest paths from the source nodes to the base node using swarm intelligence based optimization technique called ACO. A multi-path data transfer is also accomplished to provide reliable network operations, while considering the energy levels of the nodes. Wireless Sensor Network
architecture, ACO algorithm for network routing and
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1885
ISSN 2229-5518
Simulation Results are presented in the following sections.
The ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. This algorithm is a member of the ant colony algorithms family, in swarm intelligence methods, and it constitutes some metaheuristic optimizations. Initially proposed by Marco Dorigo in 1992 in his PhD thesis, the first algorithm was aiming to search for an optimal path in a graph, based on the behavior of ants seeking a path between their colony and a source of food. The original idea has since diversified to solve a wider class of numerical problems, and as a result, several problems have emerged, drawing on various aspects of the behavior of ants.
A combinatorial optimization problem is a problem defined over a set C = c1, ... , cn of basic components. A subset S of
components represents a solution of the problem; F ⊆ 2C is
the subset of feasible solutions, thus a solution S is feasible if
and only if S ∈ F. A cost function z is defined over the
solution domain, z : 2C � R, the objective being to find a
minimum cost feasible solution S*, i.e., to find S*: S* ∈ F and z(S*) ≤ z(S), ∀S∈F. Given this, the functioning of an ACO
algorithm can be summarized as follows:-
A set of computational concurrent and asynchronous agents (a colony of ants) moves through states of the problem corresponding to partial solutions of the problem to solve. They move by applying a stochastic local decision policy based on two parameters, called trails and attractiveness. By moving, each ant incrementally constructs a solution to the problem. When an ant completes a solution, or during the construction phase, the ant evaluates the solution and modifies
the trail value on the components used in its solution. This
pheromone information will direct the search of the future ants. Furthermore, an ACO algorithm includes two more mechanisms: trail evaporation and, optionally, daemon actions. Trail evaporation decreases all trail values over time, in order to avoid unlimited accumulation of trails over some component. Daemon actions can be used to implement centralized actions which cannot be performed by single ants, such as the invocation of a local optimization procedure, or the update of global information to be used to decide whether to bias the search process from a non-local perspective. More specifically, an ant is a simple computational agent, which iteratively constructs a solution for the instance to solve. Partial problem solutions are seen as states. At the core of the ACO algorithm lies a loop, where at each iteration, each ant moves (performs a step) from a state ι to another one ψ, corresponding to a more complete partial solution. That is, at each step σ, each ant k computes a set Ak σ(ι) of feasible expansions to its current state, and moves to one of these in probability. The probability distribution is specified as follows. For ant k, the probability pιψk of moving from state ι to state ψ depends on the combination of two values:
• the attractiveness ηιψ of the move, as computed by some heuristic indicating the a priori desirability of that move;
• the trail level τιψ of the move, indicating how proficient it has been in the past to make that particular move: it represents therefore an a posteriori indication of the desirability of that move. Trails are updated usually when all ants have completed their solution, increasing or decreasing the level of trails corresponding to moves that were part of "good" or "bad" solutions, respectively.
The first ACO algorithm was called the Ant system and it was aimed to solve the travelling salesman problem, in which the goal is to find the shortest round-trip to link a series of cities. The general algorithm is relatively simple and based on a set of ants, each making one of the
possible round-trips along the cities. At each stage, the
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1886
ISSN 2229-5518
ant chooses to move from one city to another according to some rules:
1. It must visit each city exactly once;
2. A distant city has less chance of being chosen
(the visibility);
3. The more intense the pheromone trail laid out on an edge between two cities, the greater the probability that that edge will be chosen;
4. Having completed its journey, the ant deposits more pheromones on all edges it traversed, if the journey is short;
5. After each iteration, trails of pheromones evaporate.
ACS was the first algorithm inspired by real ant’s behavior. The merit is used to introduce the ACO algorithms and to show the potentiality of using artificial pheromone and artificial ants to drive the search of always better solutions for complex optimization problems. In ACS once all ants have computed their tour
(i.e. at the end of each iteration) AS updates the
pheromone trail using all the solutions produced by the ant colony. Each edge belonging to one of the computed solutions is modified by an amount of pheromone proportional to its solution value. At the end of this phase the pheromone of the entire system evaporates and the process of construction and update is iterated. On the contrary, in ACS only the best solution computed since the beginning of the computation is used to globally update the pheromone. As was the case in AS, global updating is intended to increase the attractiveness of promising route but ACS mechanism is more effective since it avoids long convergence time by directly concentrate the search in a neighborhoods of the best tour found up to the current iteration of the algorithm. ANTS algorithm within the ACO frame-work has two mechanisms:
i. Attractiveness: - The attractiveness of a move can be effectively estimated by means of lower bounds (upper bounds in the case of maximization problems) on the cost of the completion of a partial solution. In fact, if a state ι corresponds to a partial problem solution it is possible to compute a lower bound on the cost of a complete solution containing ι.
ii. Trail update :- A good trail updating mechanism avoids stagnation, the undesirable situation in which all ants repeatedly construct the same solutions making any further exploration in the search process impossible. Stagnation derives from an excessive trail level on the moves of one solution, and can be observed in advanced phases of the search process, if parameters are not well tuned to the problem. The trail updating procedure evaluates each solution against the last k solutions globally constructed by ANTS. As soon as k solutions are available, their moving average z is computed; each new solution z is compared with z. If z is lower than z, the trail level of the last solution's moves is increased, otherwise it is decreased.
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1887
ISSN 2229-5518
Where z is the average of the last k solutions and LB is a lower bound on the optimal problem solution cost.
In the ACO based approach, each ant tries to find a path in the network, providing minimum cost. Ants are launched from a source node s and move through neighbor repeater nodes ri, and reach a final destination node (sink) d. Whenever, a node has data to be transferred to the destination which is described as a base or base station, launching of the ants is performed. After launching, the choice of the next node r is made according to a probabilistic decision rule (1):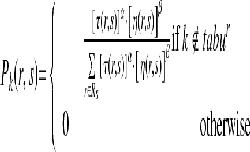 (1)
(1)
where τ (r,s) is the pheromone value, n (r,s)is the value of the heuristic related to energy, Rs is the receiver nodes. For node r, tabur is the list of identities of
received data packages previously. α and β are two parameters that control the relative weight of the pheromone trail and heuristic value. Pheromone trails are connected to arcs. Each arc(r,s) has a trail
value. τ (r,s) ∈ lsqb;0,1rsqb; Since the destination dis a
stable base station, the last node of the path is the same
for each ant travel. The heuristic value of the node r is expressed by equation (2):
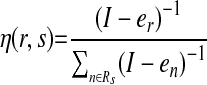 (2)
(2)
where I is the initial energy, and er is the current energy level of receiver node r. This enables decision making
according to neighbor nodes' energy levels, meaning that if a node has a lower energy source then it has lower probability to be chosen. Nodes inform their neighbors about their energy levels when they sense any change in their energy levels.
In traditional ACO, a special memory named Mk is held in the memory of an ant to retain the places visited by that ant (which represent nodes in WSNs). In equation (1), the identities of ants (as sequence numbers) that visited the node previously, are kept in the node's memories, instead of keeping node identities in ant's memories, so there is no need to carry Mk lists in packets during transmission. This approach decreases the size of the data to be transmitted and saves energy. In equation (1) each receiver node decides whether to accept the upcoming packet of ant k or not, by checking its tabu list. So, the receiver node r has a choice about completing the receiving process by listening and buffering the entire packet. If the receiver node has received the packet earlier, it informs the transmitter node by issuing an ignore message, and switches itself to idle mode until a new packet arrives.
After all ants have completed their tour, each ant k deposits a quantity of pheromone Δτk(t) given
inequation (3), where ![]() is the length of tour, wk (t)
is the length of tour, wk (t)
which is done by ant k at iteration t. The amount of pheromone at each connection ((l(r,s))of the nodes is
given in equation (4). In WSNs, ![]() represents the total number of nodes visited by ant k of tour w at
represents the total number of nodes visited by ant k of tour w at
iteration t:
![]() (3)
(3)
τ(r, s)(t) ← τ(r, s)(t)+ Δτ(r, s)(t), ∀ l(r, s) ∈ wk(t), k = 1, , m
(4)
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1888
ISSN 2229-5518
Pheromone values are stored in a node's memory. Each node has information about the amount of pheromone on the paths to their neighbor nodes. After each tour, an
amount of pheromone trail Δτk is added to the path
visited by ant k. This amount is the same for each arc(r, s) visited on this path. This task is performed by sending ant k back to its source node from the base along the same path, while transferring an acknowledgement signal for the associated data package. Increasing pheromone amounts on the paths according to lengths of tours, Jw (t) would continuously cause an increasing positive feedback. In order to control the operation, a negative feedback, the operation of pheromone evaporation after the tour is also accomplished
in equation (5). A control coefficient ρ ∈ (0,1) is used to
determine the weight of evaporation for each tour [19]:
τij(t) ← (1 − ρ)τij(t) (5)
In simulations, ACO parameter settings are set to values
2 for α, 6 for β, and 0.5 for ρ, which were experimentally found to be good by Dorigo. .
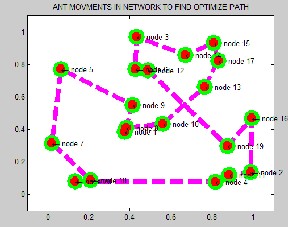
In this section, we present the performance results of the simulation experiments. To accomplish the experiments, a parallel discrete event-based platform was developed in MATLAB. The fig. 2. are represent sensor node are randomly deploy in the network and connect with each other. Fig. 3 represent the node are randomly deployed and node are in range of each other. The nodes are connected within radius of each other. The fig.4. Represent all the node is communicating in range of each other and data can be transfer in small area. The fig. 5 represents ant movement in network to find optimize path. All Sensor node are communicating
bidirectional and data can be transfer through ants.
Fig. 2. Node are deploy randomly
Fig. 3. All sensor node are in range of each other
Fig. 4. All node are communicating in range of each other
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 1889
ISSN 2229-5518
[1] J.-Y. Heo, J.-M.Hong, and Y.-K. Cho, “EARQ: Energy aware routing for real-time and reliable communication in wireless industrial sensor networks,” IEEE Trans. Ind. Informat, vol. 5, no. 1, pp. 3–11, Feb. 2009.
[2].Marco Dorigo, Mauro Bimttari, and Thomas, "Ant Colony Optimization Artificial Ants as a Computational Intelligence Technique", IRIDIA – TECHNICAL REPORT
SERIES: TRlIRIDIAI2006-023.
Fig.5. Ant movement in network to find optimize path
In this paper, Ant Colony Optimization based routing algorithm was implemented. In WSN, the life time network is depended essentially to the density and the rate of communications of sensors which affect the battery level and so the network. We act on the routing level and present a new routing algorithm, which uses ant colony optimization algorithm for WSNs. This solution improves actively the life time network of the WSN. The next work will be focused on the mobility context of sensors witch considered as a huge challenge in WSN area with energy consumption metric.
The authors also would like to thank the anonymous reviewers for their comments and suggestions to improve this paper. The authors also would like to
thanks my friends.
[3]. Camara, D.; Loureiro, AAF, "A novel routing algorithm for ad hoc networks", System Sciences, 2000.
[4]. M.Golshahi, M.Mosleh, M.Kheyrandish, "Implementing An ACO Routing Algorithm For AD-HOC Networlcs," IEEE, International Conference on Advanced Computer Theory and Engineering, 2008.
[5].Gianni Di Caro, Frederick Ducatelle and Luca Maria Gambardella, "SWARM INTELLIGENCE FOR ROUTING IN MOBILE AD HOC ETWORKS" 2005
IEEE.
[6]. Bonabeau E., Dorigo M. Natural to Artificial Systems. Oxford Univ. Press; London, U.K.: 1999. G.T. Swarm Intelligence; pp. 1–278.
[7]. White T., Pagurek B. Toward Multi-Swarm Problem Solving in Networks. International Conference on Multi Agent Systems. 1998:333–340
.
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013
ISSN 2229-5518
1890
IJSER 2013