International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 1399
ISSN 2229-5518
Quantify the Loss Reduction with Optimization of Capacitor Placement Using
ABC Algorithm- A CASE STUDY
Mahdi Mozaffari Legha, Mahdi Nazari Zadeh, Farzaneh Ostovar, Ardalan Zargar Raeiszadeh
Abstract- Increasing application of capacitor banks on distribution networks is the direct impact of development of technology and the energy disasters that the world is encountering. To obtain these goals the resources capacity and the installation place are of a crucial importance. Line loss reduction is one of the major benefits of capacitor, amongst many others, when incorporated in the power distribution system. The quantum of the line loss reduction should be exactly known to assess the effectiveness of the distributed generation. In this paper, a new method is proposed to find the optimal and simultaneous place and capacity of these resources to reduce losses, improve voltage profile too the total loss of a practical distribution system is calculated with and without capacitor placement and an index, quantifying the total line loss reduction is proposed. To demonstrate the validity of the proposed algorithm, computer simulations are carried out on actual power network of Kerman Province, Iran and the simulation results are presented and discussed.
Keywords- Distribution systems, Loss reduction index, Capacitor placement, Artificial Bee Colony
—————————— ——————————
1. Introduction
The loss minimization in distribution systems has assumed greater significance recently since the trend towards distribution automation will require the most efficient operating scenario for economic viability variations. The power losses in distribution systems correspond to about 70% of total losses in electric power systems (2005). To reduce these losses, shunt capacitor banks are installed on distribution primary feeders. The advantages with the addition of shunt capacitors banks are to improve the power factor, feeder voltage profile, Power loss reduction and increases available capacity of feeders. Therefore it is important to find optimal location and sizes of capacitors in the system to achieve the above mentioned objectives. Since, the optimal capacitor placement is a complicated combinatorial optimization problem, many different optimization techniques and algorithms have been proposed in the past. H. Ng et al (2000) proposed the capacitor placement problem by using fuzzy approximate reasoning. Ji Pyng Chiou et al (2006) proposed the variable scale hybrid differential evolution algorithm for the capacitor placement in distribution system. Both Grainger et al (1981) and Baghzouz and Ertem (1990) proposed the concept that the
————————————————
• Mahdi Mozaffari Legha, Department of Power Engineering, Shadegan Branch, Islamic Azad University, Iran. Mobile: +989132994592. (E-mail: Mahdi_mozaffari@mailfa.org).
• Ardalan Zargar Raeiszadeh, Department of Power Engineering, Kerman
Branch, Science and Research, Islamic Azad University, Iran Tel:
+989121329492. (E-mail: Ardalan.zargar@yahoo.com).
size of capacitor banks was considered as a continuous variable.
However, considered only the losses in the lines and the quantification were defined for the line losses only. These indices, therefore, do not indicate the loss reduction of the system itself. A practical distribution system consists of several distribution transformers, supplying consumers at low voltage on the secondary side. The losses occurring in these transformers and the line losses of the secondary low voltage distribution system should also be considered to arrive at the overall loss reduction of the system.
In this paper, a new method is proposed to find the optimal and simultaneous place and capacity of these resources to reduce losses, improve voltage profile too the total loss of a practical distribution system is calculated with and without capacitor placement and an index, quantifying the total line loss reduction is proposed. To demonstrate the validity of the proposed algorithm, computer simulations are carried out on actual power network of Kerman Province, Iran and the simulation results are presented and discussed.
2. Objective Function
The objective of capacitor placement in the distribution system is to minimize the annual cost of the system, subjected to certain operating constraints and load pattern. For simplicity, the operation and maintenance cost of the capacitor placed in the distribution system is not taken into consideration. The three-phase system is considered as balanced and loads are assumed as time invariant. Mathematically, the objective function of the problem is described as:
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 𝑓 = 𝑀𝑖𝑛 (𝐶𝑂𝑆𝑇)
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 1400
ISSN 2229-5518
Where COST includes the cost of power loss and the
capacitor placement. The voltage magnitude at each bus must be maintained within its limits and is expressed as:
𝑉𝑚𝑖𝑛 ≤ |𝑉𝑖 | ≤ 𝑉𝑚𝑎𝑥
Therefore, for each installation location, there are L
capacitor sizes {1QC , 2Qc , 3Qc , …, LQc} available. Given the annual installation cost for each compensated bus, the total cost due to capacitor placement and power loss change is written as
𝑐
𝐿𝑂𝑆𝑆 + � �𝐾
+ 𝐾𝑐 𝑄𝑐 �
Where │Vi│ is the voltage magnitude of bus i, Vmin and
Vmax are bus minimum and maximum voltage limits,
𝐶𝑂𝑆𝑇 = 𝐾𝑝 × 𝑃𝑇
𝑐𝑓
𝑖
𝑖 𝑖
respectively.
3. Formulation
Where n is number of candidate locations for capacitor
placement, Kp is the equivalent annual cost per unit of power loss in $/(Kw-year); Kcf is the fixed cost for the
𝑐
The power flows are computed by the following set of
capacitor placement. Constant 𝐾𝑖
is the annual capacitor
simplified recursive equations derived from the single-
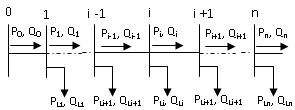
line diagram depicted in Figure. 1.
installation cost, and, i = 1, 2, ..., n are the indices of the
buses selected for compensation. The bus reactive
compensation power is limited to
𝑛
𝑐 ≤ � 𝑄𝐿𝑖
𝑖=1
Where 1Qc and LQc are the reactive power compensated
at bus i and the reactive load power at bus i, respectively.
Figure 1: Single line diagram of main feeder
4. Power Flow Analysis Method
The methods proposed for solving distribution power flow analysis can be classified into three categories: Direct
2 2
𝑃𝑖+1 = 𝑃𝑖 − 𝑃𝐿𝑖+1 − 𝑅𝑖𝑗 +1

𝑃𝑖 + 𝑄𝑖
|𝑉𝑖 |2
methods, Backward-Forward sweep methods and
Newton-Raphson (NR) methods. The Backward-Forward
2 + 𝑄2
Sweep method is an iterative means to solving the load
𝑄𝑖+1 = 𝑄𝑖 − 𝑄𝐿𝑖+1 − 𝑋𝑖𝑗+1

|𝑉𝑖 |2
flow equations of radial distribution systems which has two steps. The Backward sweep, which updates currents
2 2
|𝑉𝑖 |2 = |𝑉𝑖 |2 − 2�𝑅𝑖𝑗+1 𝑃𝑖 + 𝑋𝑖𝑗+ 𝑄𝑖 � + �𝑅𝑖𝑗+1 + 𝑋𝑖𝑗+1 �

2 + 𝑄2
× |𝑉 |2
𝑖
Where Pi and Qi are the real and reactive powers flowing
out of bus i, and PLi and Q Li are the real and reactive load
powers at bus i. The resistance and reactance of the line section between buses i and i+1 are denoted by Ri,i+1 and Xi,i+1 respectively. The power loss of the line section connecting buses i and i+1 may be computed as
using Kirchoff’s Current Law (KCL), and the Forward
sweep, which updates voltage using voltage drop
calculations [5].
The Backward Sweep calculates the current injected into
each branch as a function of the end node voltages. It
performs a current summation while updating voltages. Bus voltages at the end nodes are initialized for the first iteration. Starting at the end buses, each branch is traversed toward the source bus updating the voltage and calculating the current injected into each bus. These calculated currents are stored and used in the subsequent
2 2
𝑃𝐿𝑜𝑠𝑠 (𝑖, 𝑖 + 1) = 𝑅𝑖,𝑖+1

𝑃𝑖 + 𝑄𝑖
|𝑉𝑖 |2
Forward Sweep calculations. The calculated source
voltage is used for mismatch calculation as the termination criteria by comparing it to the specified
The total power loss of the feeder, 𝑃𝐿𝑂𝑆𝑆
may then be
source voltage. The Forward Sweep calculates node
determined by summing up the losses of all line sections
of the feeder, which is given as
𝑛−1
𝐿𝑂𝑆𝑆
voltages as a function of the currents injected into each bus. The Forward Sweep is a voltage drop calculation
with the constraint that the source voltage used is the
𝑃𝑇
= � 𝑃𝐿𝑂𝑆𝑆 (𝑖, 𝑖 + 1)
𝑖=0
specified nominal voltage at the beginning of each
forward sweep. The voltage is calculated at each bus,
Considering the practical capacitors, there exists a finite
number of standard sizes which are integer multiples of
the smallest size Q0 c. Besides, the cost per Kvar varies from one size to another. In general, capacitors of larger size have lower unit prices. The available capacitor size is usually limited to
beginning at the source bus and traversing out to the end buses using the currents calculated in previous the Backward Sweep [5].
5. Artificial Bee Colony Algorithm (ABC)
𝑚𝑎𝑥
𝑐
= 𝐿𝑄𝑐
Artificial Bee Colony (ABC) algorithm, proposed by
Karaboga for optimizing numerical problems in [6],
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 1401
ISSN 2229-5518
simulates the intelligent foraging behavior of honey bee
swarms. In ABC algorithm, the colony of artificial bees contains three groups of bees: employed bees, and unemployed bees: onlookers and scouts. In ABC, first half
current by the capacitor. Where I Cap is the current injected
by the capacitor and I i remains the same at earlier value. The total loss of the distribution system with capacitor is now
of the colony consists of employed artificial bees and the
second half constitutes the artificial onlookers. The
∑𝑁−1 𝐼𝑖 𝑖
𝑁−1
𝐿𝑜𝑠𝑠𝑤𝑖𝑡ℎ 𝐶𝑎𝑝 = ∑𝐾 −1�𝐼𝑖 − 𝐼𝐶𝑎𝑝 � 𝑟𝐿𝑖 +
employed bee whose food source has been exhausted
𝑖=𝑘
2 𝑟𝐿 + ∑𝑖=1 �𝑃𝑐𝑖 + 𝑃𝐿𝑣 �
becomes a scout bee. In ABC algorithm, the position of a food source represents a possible solution to the optimization problem and the nectar amount of a food source corresponds to the quality (fitness) of the associated solution. The number of the employed bees is equal to the number of food sources, each of which also represents a site, being exploited at the moment or to the number of solutions in the population. In the ABC algorithm, first half of the colony consists of employed artificial bees and the second half constitutes the onlookers. For every food source, there is only one employed bee. In the ABC algorithm, each cycle of the search consists of three steps: sending the employed bees onto the food sources and then measuring their nectar amounts Hence, the dance of employed bees carrying higher nectar recruits the onlookers for the food source areas with higher nectar amount. After arriving at the selected area, she chooses a new food source in the neighborhood of the one in the memory depending on visual information. Visual information is based on the comparison of food source positions. When the nectar of a food source is abandoned by the bees, a new food source is randomly determined by a scout bee and replaced with the abandoned one [12].
6. Loss Reduction Analysis
The total loss of the distribution system without capacitor is given by
A factor, loss reduction index (LRI), which quantifies the loss reduction with the insertion of capacitor, is defined as
𝐿𝑜𝑠𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑠𝑦𝑠𝑡𝑒𝑚 𝑤𝑖𝑡ℎ capacitor

𝐿𝑅𝐼 =
𝐿𝑜𝑠𝑠 𝑖𝑛 𝑡ℎ𝑒 𝑠𝑦𝑠𝑡𝑒𝑚 𝑤𝑖𝑡ℎ𝑜𝑢𝑡 capacitor
The LRI is now obtained as
𝐿𝑜𝑠𝑠𝑆𝑦𝑠𝑡𝑒𝑚 𝑤𝑖𝑡ℎ𝑜𝑢𝑡 𝐶𝑎𝑝 + 𝐾𝐿𝑜𝑠𝑠 𝐼𝐶𝑎𝑝

𝐿𝑅𝐼 =
𝐿𝑜𝑠𝑠𝑆𝑦𝑠𝑡𝑒𝑚 𝑤𝑖𝑡ℎ𝑜𝑢𝑡 𝐶𝑎𝑝
Where KLoss is the loss factor given by
𝐾−1
𝐾𝑙𝑜𝑠𝑠 = ��𝐼𝐶𝑎𝑝 − 2𝐼𝑖 � × 𝑟 × 𝐿𝑖
𝑖 =1
7. Test Results
To study the proposed method, actual power network of Kosar feeder of Kerman Province, Iran is simulated in Cymedist. Figure 2 illustrates the single-line diagram of this network. The base values of the system are taken as
20kV and 20MVA. The system consists of 20 distribution
transformers with various ratings. The details of the distribution transformers are given in table 1. The details of the distribution conductors are given in table 2. The lengths of the feeder segments are given in table 3. The total connected load on the system is 2550 KVA and the peak demand for the year is 2120 KVA at a PF of 0.8 lag.
𝑁−1
𝑁−1
2 × 𝑟 × 𝐿 + � �𝑃
+ 𝑃 �
The connected loads on the transformers are listed in
𝐿𝑜𝑠𝑠 𝑤𝑖𝑡ℎ𝑜𝑢𝑡 𝐶𝑎𝑝 = � 𝐼𝑖

𝑖 =1
𝑖
𝑖 =1
𝑐𝑖
𝐿𝑣 𝑖
table 4.
Where I i is the current flowing through ith section, r is
the resistance of line in ohms per unit length, Li is the
length of ith section, Pci is the core loss of ith transformer,
PLvi is the Losses on the low voltage side of the ith
transformer and N is the number of busses in the system.
In order to determine the losses of the system, the core
loss of each transformer and the LV side losses on each transformer must be known. It is evident from the above equation that the total losses can be reduced only by reducing the first term which represents the feeder line losses, since the other term representing the core loss and the LV side loss of each transformer remain same independent of the presence of capacitor. If a capacitor is inserted at Kth bus, the feeder segments up to bus K will carry the difference of the initial current and the injected
IJSER © 2013 http://www.ijser.org
Figure 2: Single-line diagram of actual power network of Kosar feeder of Kerman Province in Cymedist
Table 1: Details of transformers in the system
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 1402
ISSN 2229-5518
[watts] | | | |
Impedance [%] | 4.5 | 4.5 | 4.5 |
Table 2: Details of conductors in the system
Type | R [Ω/km] | X [Ω/km] | Cmax [A] | A [mm2] |
Hyena | 0.1576 | 0.2277 | 550 | 126 |
Dog | 0.2712 | 0.2464 | 440 | 120 |
Mink | 0.4545 | 0.2664 | 315 | 70 |
Table 3: Distribution System Line Data
Initially, a load flow was run for the case study in both
fundamental frequency and harmonics frequencies without installation of capacitor. Table 5 depicts the results of power flow for determination voltage and harmonic before installation of capacitor. Table 6 depicts the locations and capacity of capacitor banks using artificial bee colony algorithm. As it is clear, all the obtained values confines with all the considered constraints. The obtained penetration lever is 0.27, which is less than the assumed allowable value.
Table 5: Results of power flow before installation of
capacitor
from | To | Length (meters) |
1 | 2 | 80 |
2 | 3 | 80 |
3 | 4 | 80 |
4 | 5 | 60 |
5 | 6 | 60 |
6 | 7 | 60 |
7 | 8 | 60 |
8 | 9 | 60 |
9 | 10 | 60 |
10 | 11 | 60 |
11 | 12 | 60 |
12 | 13 | 60 |
13 | 14 | 60 |
14 | 15 | 60 |
14 | 16 | 60 |
16 | 17 | 60 |
17 | 18 | 60 |
18 | 19 | 60 |
19 | 20 | 60 |
Table 4: Details of the connected loads
Table 6: Optimal place and capacity of capacitor banks
In addition the total network loss, which was 10.05MW
before installing capacitor, has diminished to the 4.55MW which shows 45.81% decrease. Table 7 shows the impact of installing capacitor on THD of buses.
Table 7: Results of power flow after installation of capacitor banks
Bus Number | V (pu) |
1 | 1.0 |
2 | 0.9999 |
3 | 0.9999 |
4 | 0.9999 |
5 | 0.9999 |
6 | 0.9988 |
7 | 0.9988 |
8 | 0.9888 |
9 | 0.9881 |
10 | 0.9885 |
11 | 0.99 |
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 1403
ISSN 2229-5518
12 | 0.97 |
13 | 0.91 |
14 | 0.988 |
15 | 0.988 |
16 | 0.95 |
17 | 0.96 |
18 | 0.98 |
19 | 0.95 |
20 | 0.93 |
The detailed pu voltages profile and Percentage of loss of all the nodes of the system before and after capacitor
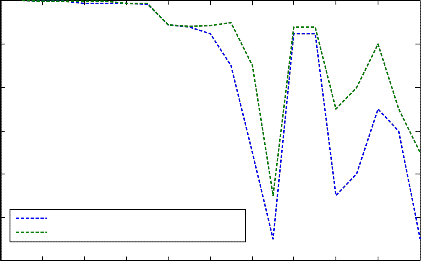
placement are shown in the Figure 3 and Figure 4. The
simulation results are given in Table 8. The simulation results are given in Table 8. These results reveal that the inclusions of capacitor reduce the line losses as expected. It can be shown from the graphs that, LRI decreases marginally, since the core losses of the transformers and the LV side losses remain constant being independent of the presence of v. It can also be seen that with the increase in the reactive power of capacitor, LRI, decrease.
1
0.98
0.96
0.94
0.92
0.9
Voltages profile before capacitor placement
Voltages profile after capacitor placement
0.88
0 2 4 6 8 10 12 14 16 18 20
Bus Number

Figure 3: Voltage profile of 20 bus system before and after capacitor placement
losse without capacitor
losse with capacitor
43%
57%
Figure 4: Percentage of loss before and after capacitor placement
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 1404
ISSN 2229-5518
Table 8: Variation of LRI and capacity & number of capacitor banks
Number | 3 | 3 | 5 | 5 | 7 | 7 |
place | 2,12,16 | 7,13,15 | 2,6,7,13,15 | 7,8,9,11,20 | 5,7,13,15,16,18,20 | 2,4,9,10,14,18,20 |
Picked capacity [Mvar] | 0.02 | 0.02 | 0.575 | 0.35 | 2.1 | 2.25 |
Presumable Capacity Range [Mvar] | 0.025 0.05 0.1 0.2 0.25 0.4 0.5 | 0.05 0.1 0.2 0.4 0.5 0.8 1 | 0.025 0.05 0.1 0.2 0.25 0.4 0.5 | 0.05 0.1 0.2 0.4 0.5 0.8 1 | 0.025 0.05 0.1 0.2 0.25 0.4 0.5 | 0.05 0.1 0.2 0.4 0.5 0.8 1 |
LRI [%] | 0.9296 | 0.8866 | 0.7627 | 0.6649 | 0.7026 | 0.9754 |
8. Conclusion
In the present paper, a new population based artificial bee colony algorithm (ABC) has been proposed to solve capacitor placement problem and quantifying the total line loss reduction in distribution system. Simulations are carried on actual power network of Kerman Province, Iran. The simulation results show that the inclusion of capacitor, marginally reduce the losses in a distribution system. This is because; the line losses form only a minor part of the distribution system losses and the capacitor can reduce only the line losses. The other losses viz. the transformer losses and the LV side distribution losses remain unaltered. Hence this fact should be considered before installing a capacitor into a system. The results obtained by the proposed method outperform the other methods in terms of quality of the solution and computation efficiency.
9. References
[1] C. Lyra, C. Pissara, C. Cavellucci, A. Mendes, P. M. Franca (2005), “Capacitor placement in large sized radial distribution networks, replacement and sizing of capacitor banks in distorted distribution networks by genetic algorithms”, IEE Proceedings Generation, Transmision & Distribution, pp. 498-516.
[2] Ng H.N., Salama M.M.A. and Chikhani A.Y (2000), “Capacitor allocation by approximate reasoning: fuzzy capacitor placement”, IEEE Transactions on Power Delivery, vol. 15, No. 1, pp. 393-398.
[3] Sundharajan and A. Pahwa (1994), “Optimal selection of capacitors for radial distribution systems using genetic algorithm”, IEEE Trans. Power Systems, vol. 9, No.3, pp.1499-1507.
[4] Ji-Pyng Chiou et al(2006), “Capacitor placement in large scale distribution system using variable scaling hybrid differential evolution”, Electric Power and Energy Systems, vol. 28, pp.739-745.
[5] M. Mozaffari Legha, (2011) Determination of exhaustion and junction of in distribution network and its loss maximum, due to geographical condition, MS.c Thesis. Islamic Azad University, Saveh Branch, Markazi Province, Iran.
[6] J. L. Bala, P. A. Kuntz, M. Tayor (1995), “Sensitivity-based optimal capacitor placement on a radial distribution feeder”, Proc. Northcon 95, IEEE Technical Application Conf., pp. 225230.
[7] D. Karaboga, B. Basturk (2007), “A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm”,Journal of Global Optimization, vol. 39, pp. 459-471.
[8] D. Karaboga, B. Basturk(2008), “On the performance of artificial bee colony (ABC) algorithm”, Applied Soft Computing, vol. 8 pp. 687-
697.
[9] Prakash K. and Sydulu M (2007), “Particle swarm optimization based capacitor placement on radial distribution systems”, IEEE Power Engineering Society general meeting 2007, pp. 1-5.
[10] D. Das (2002), “Reactive power compensation for radial distribution networks using genetic algorithms”, Electric Power and Energy Systems, vol. 24, pp.573-581.
[11] K. S. Swarup (2005),”Genetic Algorithm for optimal capacitor allocation in radial distribution systems",Proceedings of the 6th WSEAS Int. Conf. on EVOLUTIONARY COMPUTING, Lisbon, Portugal, June 16-18, pp152-159.
[12] D. Karaboga, B. Basturk(2008), “On the performance of artificial bee colony (ABC) algorithm”, Applied Soft Computing, vol. 8 pp. 687-
697.
[13] Chiradeja, Ramkumar , “ An Approach to quantify the Benefits of Distrributed Generation Systems”, IEEE trans. On Energy Conversion, Vol. 19, Dec 2004, pp 764 – 773.
[14] B. Basturk, D. Karaboga (2006), “An artificial bee colony (ABC) algorithm for numeric function optimization”, IEEE Swarm Intelligence Symposium 2006, May 12-14, Indianapolis, IN, USA.
IJSER © 2013 http://www.ijser.org



