International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 1

ISSN 2229-5518

Photovoltaic Solar Energy: Review

A.M.K. El-Ghonemy

Engineering College, Al-Jouf University, KSA.

Email : amghonemy@yahoo.com .

Abstract

Energy is one of the most important topics on the international environment and development agenda. The sun is the
largest energy source of life while at the same time it is the ultimate source of most of renewable energy sources. Solar energy can be used to generate electricity in a direct way with the use of photovoltaic (PV) modules. Photovoltaic is defined as the generation of electricity from light. The technology of photovoltaic cells was developed rapidly over the past few decades. Nowadays the efficiency of the best crystalline silicon cells has reached 24% for photovoltaic cells under laboratory conditions and for that used in aerospace technology and about 14-17% overall efficiency for those available commercially while modules costs dropped to below 4$ per watt peak (4$/WP).
The present paper presents a review for the work that has been achieved during the recent years in the field of PV systems,
with emphasis on technologies, performance and economics. The review also includes PV modeling and simulation. A comparative study between different PV technologies as well as performance and economics has been done. In addition, the maximum power point tracker (MPPT) for PV system was focused, to maximize its performance. Finally, some general guidelines are given for selection of PV systems and the parameters that need to be considered.

Keywords: Photovoltaic, construction, types, performance, economics, sizing, modeling, Simulation, MPPT, review

1. Introduction

The concentration on the use of fossil fuels for energy
supply is the main threat for the stability of the global climate system and our natural living conditions. To conserve our globe, the scientific community gave evidence that mankind has to decrease the green house gases emissions, mainly CO2 and methane, by 60 - 70% as a minimum until the year 2050 [1]. In order not to harm our natural living spaces and threaten their resilience, a renewed compatibility would require a suitable form of energy alternatives sources that should be independent, easily accessible, and low in cost and should be environmentally clean.
Renewable energy, and in particular power generation from solar energy using Photovoltaic (PV) has emerged in last decades since it has the aforesaid advantages and less maintenance, no wear and tear. The main applications of PV systems are in either stand-alone systems such as water pumping, domestic and street lighting, electric vehicles, military and space applications or grid-connected configurations like hybrid systems and power plants [1].
The sun is the largest energy source of life while at the same time it is the ultimate source of most of renewable energy sources. Solar energy can be used to generate electricity in a direct way with the use of photovoltaic modules. Photovoltaic is defined as the generation of electricity from light where the term photovoltaic is a compound word and comes from the Greek word for light, photo, with, volt, which is the unit of electromotive power. The technology of photovoltaic cells was developed rapidly over the past few decades. Nowadays the efficiency of the best crystalline silicon cells has reached 24% for photovoltaic cells under laboratory conditions and for that used in aerospace technology and
about 14-17% overall efficiency for those available commercially while modules costs dropped to below 4$ per watt peak (4$/WP) [1].
Global PV module production is growing rapidly. Although the market is dominated by crystalline silicon modules, non-crystalline silicon modules are rapidly
penetrating the PV market. Besides various types of amorphous silicon modules with multi-junction layers, modules based on new technologies are introduced, such
as CIS or CdTe.

1.1-Solar resource

Knowledge of the sun is very important in the
optimization of photovoltaic systems [2]. Solar energy is the most abundant renewable resource. The electromagnetic waves emitted by the sun are referred to as solar radiation. The amount of sunlight received by any surface on earth will depend on several factors including; geographical location, time of the day, season, local landscape and local weather. The light's angle of incidence on a given surface will depend on the orientation since the Earth's surface is round and the intensity will depend on the distance that the light has to travel to reach the respective surface. The radiation received by a surface will have two components one which is direct and will depend on the distance the rays travel (air mass). The other component is called diffuse radiation and is illustrated in figure (1). The range of wavelengths of light that reach the earth varies for 300nm to 400nm approximately [3]. This is significantly different from the spectrum outside the atmosphere, which closely resembles 'black body' radiation, since the atmosphere selectively absorbs certain wavelengths.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 2

ISSN 2229-5518

Direct Beam

Cloud and dust etc.

Diffuse sunlight

1. The reference vertical irradiance Eo with a typical value of 1000W/m2
2. Reference cell temperature for performance rating, To with a typical value of 25 0C and a tolerance of ±2 0C;
3. A specified light spectral distribution with an air mass, AM =1.5. Air mass figures provide a relative measure of the path the sun must travel through the atmosphere. In addition to supplying performance parameters at the
Standard Test Conditions manufacturers also provide performance data under the Nominal Operating Cell
Temperature (NOCT) [4]. This is defined as the temperature reached by the open circuited cells in a module under the following conditions:
-Irradiance on cell surface is 800 W/m2
- The ambient temperature is 200C (293 K)

Figure (1): Types of radiation from the sun [3]

1.2-PV History

- Wind speed is 1m/s and the mounting is open back side
To account for other ambient conditions the approximate expression below may be used:

The history of PV dates back to 1839 when a

French physicist, Edmund Becquerel, discovered

Tcell

 Tamb

 NOCT  20 G
0.8

the first photovoltaic effect when he illuminated a metal electrode in an electrolytic solution [16]. Thirty-seven years later British physicist, William Adams, with his student, Richard Day, discovered a photovoltaic material, selenium, and made solid cells with 1~2% efficiency which were soon widely adopted in the exposure meters of camera [16].

In 1954 the first generation of semiconductor silicon-based PV cells was born, with efficiency of

6% [3], and adopted in space applications. Today, the production of PV cells is following an exponential growth curve since technological advancement of late ‘80s that has started to rapidly improve efficiency and reduce cost.

1.3-Spectrum of the sun

Two different spectral distributions have been defined for the sun. The AM0 spectrum relates to radiation in outer space and the AM 1.5 G spectrum is at sea level at certain standard conditions. The photovoltaic (PV) industry and the American Society for Testing and Materials (ASTM), American government research and development laboratories have developed and defined two standard terrestrial solar spectral irradiance distributions: a standard direct normal and a standard total spectral irradiance. An instrument called the pyranometer is used to measure global radiation. This instrument is designed to respond to all wavelengths and therefore gives an accurate value of the total power in any incident spectrum.

1.4-Standard test conditions (STC)

Uniform conditions are usually specified so that a
performance comparison can be made between different PV units (cell, modules). The parameters obtained from the testing are usually provided on the manufacturer's datasheet. Measurements are performed under these standard test conditions and the electrical characteristics obtained characterize the module accurately under these conditions. The conditions are specified as follows:
Where Tcell is cell temperature (0C), Tamb is the ambient temperature, (NOCT) is the Nominal Operating Cell Temperature and G is the solar insolation (kW/m2).

1.5-How do solar panels work?

Solar panels are made up of photovoltaic cells that
convert sunlight directly into electricity by using a semiconductor, usually made of silicon. The term photovoltaic comes from the Greek meaning “light” (photo) and “electrical” (voltaic). When the sunlight hits the photovoltaic cells, part of the energy is absorbed into the semiconductor. When that happens the energy loosens the electrons which allow them to flow freely. The flow of these electrons is a current and when you put metal on the top and bottom of the photovoltaic cells, we can draw that current to use it externally.

1.6-Advantages of PV powered systems

PV systems are highly reliable and are often chosen
because they offer the lowest life-cycle cost, especially for applications requiring less than 10KW, where grid electricity is not available and where internal-combustion engines are expensive to operate [1]. If the water source is 1/3 mile (app. 0.53Km) or more from the power line, PV is a favorable economic choice [1]. Table (1) shows the comparisons of different stand-alone type water pumping systems.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 3

ISSN 2229-5518

Table 1-1: PV powered, Diesel powered, vs. Windmill

[1]

1.7-objectives

The main aim of this paper is to provide a
comprehensive review about photovoltaic systems. The study was extended to include Photovoltaic construction, types, performance, economics, sizing, modeling, and Simulation. Also, the principle and operation of the PV cell and the fundamental characteristics of PV cell are discussed. Finally, a special attention was given to focus on the following points:
-Potential of solar energy
-PV materials
-Future and Market growth of Solar Panels
-Photovoltaic performance
-Photovaltaic systems
-PV hierarchy
-Photovaltaic technology
-Photovoltaic Electrical System
-Factors Affecting PV Output
-Solar Cell Limitation
-Components sizing of PV system
-Economic evaluation
-Modeling and simulation
-Maximum Power Point Tracker (Load type effect, Algorithms, control and Limitations)

2-Potential of solar energy

Energy experts expect that in the year 2050, over 50%
and 80% of all electricity could be generated by renewable energy . Among the potential sources of renewable energy, solar thermal power plants are considered to be one of the most economic.
The understanding of each technology and its associated challenges will provide a suitable basis to recognize advantages and drawbacks. The Annual horizontal solar energy available (kWh/m2) and relative peak value (W/m2) in some countries is given in table (2) [1].

Table (2): The Annual horizontal solar energy available in some countries [1].

2.1-Solar radiation in KSA:

Assessment of solar radiation resources in different
cities of KSA is given in table (3). The daily and annual distribution pattern of solar energy at given locations are essential not only for assessing the economic feasibility of solar energy utilization, but also for the thermal design and environmental control of buildings and greenhouses.
The solar radiation data for the Northern of KSA (SKAKA region) were obtained from the NASA surface meteorology and solar energy Web site [1]. The Average solar data over a 1-year period was obtained and plotted in figure (2). From these results, the average solar

2

radiation is 5.77, 7.22 kWh/m /day for horizontal and
tilted plane respectively. Moreover, the annual average daylight hours are 12 hrs. A brief list of solar energy projects that has been applied in KSA is given in Appendix-A

Table (3): solar radiation resources in different cities of

KSA[10,11]

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 4

ISSN 2229-5518

Average solar data for SKAKA areas

35

30

25

20

15

10

5

0

Month

Figure (2): Average solar data over a 1-year period

For Northern of KSA (SKAKA area) [10,11].

3-PV materials

H hori H tilted Ta PSSH

such as glass, metal or plastic. Epitaxial processes (such as vapor deposition, sputter processes and electrolytic baths) are used to achieve this. Because thin-film materials have high absorptivity, the deposited layer of PV material is extremely thin. This results in the reduction of the dominating material cost although thin- film PV cells suffer from poor cell conversion efficiency. There are several types of thin-film materials [5].

-Amorphous silicon

This material has a significant advantage of higher
light absorptivity. About 40 times that of crystalline silicon. It can be deposited on a low cost substrate and the manufacturing process requires low temperature and therefore less energy. It has lower material and manufacturing costs. Amorphous hydrogenated silicon (a-Si:H) has been widely used by the Japanese to power
PV cells are made of semiconductor materials with crystalline and thin films being the dominant materials. The majority of PV-cells are silicon-based but in the near future other thin film materials are likely going to surpass silicon PV cells in terms of cost and performance [2]. PV materials may fall into one or more of the following classes: crystalline, thin film, amorphous, multi-junction, organic or photochemical.

3-a-Crystalline materials

-Single-crystal silicon

Mono-crystalline silicon cells have in the past dominated the PV market but have now been overtaken
by poly-crystalline silicon. The popularity of mono- crystalline silicon was due to the good stability and desirable electronic, physical and chemical properties of
silicon. Moreover, silicon was already successful in microelectronics and the enormous industry thus created
would benefit the smaller PV industry with regards to
economy of scale [2].

-Poly-crystalline silicon

This is the currently most dominant material and has
surpassed the mono-crystalline because it is cheaper. The cost of silicon is a significant portion of the cost of the solar cell. The manufacturing processes of poly- crystalline silicon reduce the cost of silicon by avoiding pulling in the manufacturing process and it results in a block with a large crystal grain structure. This results in cheaper cells with a somewhat lower efficiency. The assembly of multi-crystal wafers is easier and therefore offsets the low efficiency disadvantage.

-Gallium Arsenide

This material is a compound semiconductor made of gallium and arsenic. It has a crystalline structure and has
a high level of light absorptivity. GaAs has higher efficiency than silicon but its main drawback is its cost. It is used in space applications and in concentrator systems.

3.b-Thin-film materials

Since the 1990s development of thin-film, processes for manufacturing solar cells have increased. These PV
devices are made using very thin semiconductor films deposited on some type of low-cost structural substrate
small consumer goods such as watches and calculators
[5]. This material is a non-crystalline for silicon and does not form a regular crystal structure, but an irregular network. The material is highly defective even with hydrogenation so the minority carrier lifetimes are very low resulting in low conversion efficiency. A major drawback of this material is that it degrades under sun exposure, a mechanism called the Staebler-Wroski effeect.

-Cadmium Telluride (CdTe)

This is one of the most promising thin _lm solar cells.
The material is a poly-crystalline semiconductor compound made of cadmium and tellurium. CdTe has the lowest production cost among the current thin-film technologies. Low-cost soda-lime glass is used as the substrate. The manufacturing processes have greatly improved over the past few years. The CdS film is grown either by chemical bath deposition (CBD), close space sublimation (CSS), chemical vapor deposition (CVD), sputtering, or vapor transport deposition (VTD). This material has a very high absorption coefficient.

-Copper Indium Diselenide (CIGS)

CIGS is a polycrystalline semiconductor compound of
copper, indium and selenium, and has been a major research area in the thin film industry. It is another promising material for thin-film solar cells. It can achieve high energy conversion efficiency and does not suffer from outdoor degradation problem and has demonstrated that thin film PV cells are a viable and competitive choice for the solar industry in the future.
This material also has a high absorption coefficient with only 0.5 micrometers needed to absorb 90% of the solar spectrum. However it is a very complex material making it difficult to manufacture. Moreover its manufacturing process involves hydrogen selenide, an extremely toxic gas raising safety concerns.

4-Future and Market growth of Solar

Panels

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 5

ISSN 2229-5518

4.1-History of PV market

Solar energy production has been doubling every two
years, increasing by an average of 48 percent each year since 2002, making it the world’s fastest-growing energy technology. One day of sunshine produces enough energy to power the planet for a year and solar panel technology is improving drastically to harness this powerful source of clean energy. The cost of electricity from your utility company is always going to go up, and as the demand for solar panels grow, the less expensive they will become.
The worldwide increase in PV module shipments and the breakdown into technology types can be seen in figure(3).The large increase in production of the newer thin film modules is clearly apparent . the PV industry
grew by 380% between 1998 and 2003, and the annual growth is also increasing, with module shipments increasing by approximately 33 % from 2002 to
2003[6].The crystalline silicon technologies have more
than 90% of the market share of module shipments but figure(3) shows increased production of other technologies such as a-Si and CdTe. Many factors contribute to interest in thin film technologies. These factors include: improved efficiency and efficiency stability, lower cost of manufacture and the potential to manufacture the thin film devices in large area sheets and with a flexibility that is not provided by conventional cells made on crystalline wafer substrates

Figure (3): History of total world module shipments.[6]

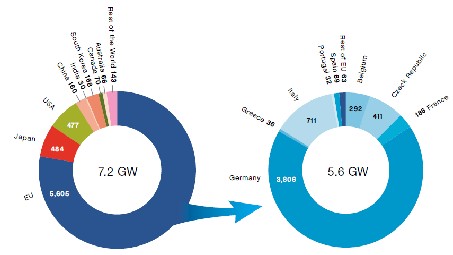
Figure (4): World and European PV markets in 2009 in MW [7].

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 6

ISSN 2229-5518

Table (4): Confirmed terrestrial module efficiencies measured under the global AM1.5 spectrum [5]

The future of the Photovoltaic industry is promising as the efficiency of the cell and sub-modules continues to increase. The table (4) shows the most recent confirmed efficiency of modules of various photovoltaic materials [7]. As technology and manufacturing processes continue to improve higher efficiencies are expected in the near future.
Bulk crystalline Si devices are likely going to remain dominant for the next decade. Thin-_lm technologies are maturing fast and may soon challenge the market share of crystalline Silicon devices. The dominant future technology will be determined largely by material availability and costs.
The increase of conventional energy prices has increased the investment attention for renewable energies and in particular photovoltaics significantly. Since 2006 the investments and growth in thin film photovoltaics have surpassed the already high growth rates of the whole photovoltaics industry but have recently slowed due to technology and financial reasons.
Thin film solar cells still offer the possibility of reducing the manufacturing costs considerably; however, considering the increasing maturity of wafer-based production technologies, observed learning curves, and recent cost reductions, newcomers have to enter the game at already very competitive levels. In addition, the entry ticket, that is, factory size for thin film manufacturers into the market, has increased from a 20MW factory in 2006 to a minimum of 100MW in 2011and is still growing with the increasing market volume[7].
Thin film technologies still need a lot of research over a wide range of issues, ranging from improvement of the understanding of basic material properties to advanced production technologies and the possible market perspectives. To tackle these problems, a long-term vision for photovoltaics and long-term research are needed.
However, there is no “winning technology” and a viable variety of technology options have to be ensured. To focus on any single technology option now could be a road block in the future. Public research funding structures should take into account that different technologies are at different development stages and need different kind of support measures.
In order to realise high production volumes for PV we must now look towards already available high- throughput, high-yield production technologies analysing
if and how they can be utilised for PV in the future. This is especially important for thin film solar cell materials, that have only a limited backing by other industries, such as that provided by the microelectronic industry, in the development of production technologies for silicon solar cells. In addition, there are a number of research issues common to all thin film technologies which have to be solved. No single solar cell technology can neither satisfy the world-wide demand nor all the different wishes consumers have for the appearance or performance of PV systems.

4.2-PV Market size by country in 2009[2]

The European Union represented 5.6 GW or 78% of
the World PV market in 2009(figure (4)). And in Europe itself, the German market clearly dominates with 68 % of the EU market. The emergence of Italy as a major market for PV, combined with the ramp-up of France and the impressive growth of the Czech Republic and Belgium, compensated the slowdown of the Spanish market. One major change in 2009 is the emergence of new markets outside Europe, with Canada and Australia starting to develop while Japan and the USA show both a significant potential in becoming new GW markets in the coming years.

4.3- PV production size by country and technology in 2009, figure (5)[6,7].

In 2009, the regional distribution of production
capacities differed significantly depending on the type of product and its position in the value chain. C-Si cells and modules production capacity seemed to be dominated by Chinese and Taiwanese manufacturers (above 50% in both cases). European production capacity counted for
almost 20% for c-Si cells and almost 30% for c-Si
modules. In Japan, both figures are below 10% whereas the USA production counts for only 5%. The picture is different when considering solar grade silicon production capacity with up to 40% in the USA, followed by Europe and China, both having similar levels of production capacity (almost 20%) and Japan and the rest of Asia (both slightly above 10%). With respect to Thin Film production capacities, Europe leads with around 30%, whereas China, the USA, Japan and the rest of Asia (mainly Malaysia) each count for about 10 to 20% of Thin Film production capacities.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 7

ISSN 2229-5518

that during the silicon shortage over the last few years, many companies invested in Thin Film production facilities. Manufacturers are still ramping up, optimising the production and/or struggling to get to the optimal cost structure to be competitive. This is especially challenging with much lower prices of polysilicon which result in lower prices for c-Si modules.

Figure (5) - Production of Silicon, c-Si cells, c-Si Modules and Thin Film modules by geographies in 2009[7]

4.4-PV technology development, figure (6)[7]

The level of announced capacities in 2009 was around
24 GW. EPIA expects these announced capacities to grow by about 30% in 2010 after which the year-to-year growth rate will level off to about 20% during later years to reach above 65 GW in 2014. The CAGR for c-Si modules will be about 22% whereas for Thin Film modules it will be
around 25%.
In 2009, the share of Thin Film in terms of capacity was around 22%. We expect this share to grow to 25% in
2013. While future capacity expansion of Si based Thin Film technologies will take place in China and Taiwan, other technologies’ production capacities (CdTe, CI(G)S) are expected to remain in the EU, the USA and Japan.
The share of Thin Film in terms of actual production was lower (slightly below 20%) and was mainly driven by CdTe production from one single company (representing above 70% of the total Thin Film module production in 2009). For other Thin Film technologies (and especially for Si based Thin Film) the production was significantly lower whereas production capacity was not (showing low capacity utilisation rates). The reason is

Figure (6): Production Capacity Outlook – Crystalline and

Thin Film technologies (Technologies with market share below 0.5% are not represented)[6,7].

4.5-Market forecasts until 2015[1]

Actual and planned PV production capacities of thin film and crystalline silicon-based solar modules are plotted in fig.(7).The

figure shows that, thin-film production capacity could be

around 17GW, or 19% of the total 88GW, in 2012 and about 27GW, or 24%, in 2015 of a total of112GW (Figure 7).

The actual production and planned capacities of the different thin film technologies are shown in figure(8).From this figure it is clear that, the dominating thin film technology in the market in 2011 is CdTe with about 2.1GW followed by thin film silicon with 2GW and CIGSSe with 0.6GW as shown in fig.(8). In terms of planned capacity increases, thin film silicon is leading followed by CIGSSe and CdTe.

The technology as well as the company distribution varies significantly from region to region (Figure 9). This regional distribution reflects on the one hand the scientific knowledge base concerning the different thin film technologies and also the investment options and availability of human resources.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 8

ISSN 2229-5518

Figure (7): Actual and planned PV production capacities of thin film and crystalline silicon-based solar modules [7].

Figure (8): Actual production and planned capacities of the different thin film technologies [7].

Figure (9): Projected (planned) thin film PV production capacities, Regional distribution of the different technologies [6,7].

5 -Photovoltaic performance

5.1-PV characteristics

There are three classic parameters that are very
important on the PV characteristics namely short-circuit current (Isc), open-circuit voltage (Voc) and the maximum power point (Imp; Vmp). The power delivered by a PV cell attains a maximum value at the points (Imp; Vmp). The classical points are shown in Figure (10) and are usually given as part of a manufacturer's data sheet for a PV module as shown in Table (5). This information is enough to build a simple model of the module to test

Isc,

Short circuit current

Module

Current, I

Vmp, Imp

Max. Power point

Open circuit

Voltage, Voc

power converters, but for a more accurate model more information is required.

Module voltage,

Figure (10): Photovoltaic module I-V curve classical points

[5]

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 9

ISSN 2229-5518

Another important parameter of the PV characteristics is called the Fill Factor (FF) is shown in Figure (11). It is a term that describes how the curve fills the rectangle that is defined by (Voc) and (Isc). It gives an indication of the quality of a cell's semiconductor junction and measures of how well a solar cell is able to collect the carriers generated by light. It is defined as:

Vmpp I mpp

FF 

VocI oc

Where, Impp, Vmpp are the current and voltage at max power point respectively

-PV General Specs and Thermal Characteristics:

The following parameters can be obtained from thev PV
data sheet (by manufacturer)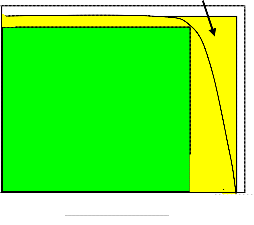

Area A

Table (5): PV Electrical characteristics provided on a datasheet[5]

Area B

I

FF=Area B/ Area A

Module voltage,

Voc

6-Photovaltaic systems

Photovoltaic systems are composed of interconnected
components designed to accomplish specific goals ranging from powering a small device to feeding electricity into the main distribution grid. Photovoltaic systems are classified according to the diagram in Figure (12). The two main general classifications as depicted in the figure are the stand-alone and the grid-connected systems [5]. The main distinguishing factor between

Figure (11): Photovoltaic module characteristics showing

the FF factor[5]

It can be easily observed that FF is always < 1 and
ranges from material to material. The closer the value of the fill factor is to unity, the better the operation of the PV cell. For high quality cells, fill factors over 0.85 can be achieved (see Table (4). For typical commercial devices the value lies around 0.68.

-PV efficiency

The efficiency η is defined as the ratio of

the maximum output power Pmp to the solar power received by the cell surface, PL:

Vmp p I mp p

 

PL

where Vmpp ,and Impp are the voltage and current at maximum power point,

-PL is

these two systems is that in stand-alone systems the solar energy output is matched with the load demand. To cater for different load patterns, storage elements are generally used and most systems currently use batteries for storage. If the PV system is used in conjunction with another power source like a wind or diesel generator then it falls under the class of hybrid systems. The balance of system (BOS) components are a major contribution to the life cycle costs of a photovoltaic system. They include all the power conditioning units, storage elements and mechanical structures that are needed. They especially have a huge impact on the operating costs of the PV system.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 10

ISSN 2229-5518

Figure (12): Classification of PV systems [5]

7-PV hierarchy

7.1-PV cell

PVs generate electric power when illuminated by
sunlight or artificial light. To illustrate the operation of a PV cell the p-n homojuntion cell is used. PV cells contain a junction between two different materials across which there is a built in electric field. The absorption of photons of energy greater than the band gap energy of the semiconductor promotes electrons from the valence band to the conduction band, creating hole-electron pairs

k is the Boltzmann’s constant (1.381×10-23 J/K),

T is the junction temperature in Kelvin (K).

throughout the illuminated part of the semiconductor [5].
These electron and hole pairs will flow in opposite directions across the junction
thereby creating DC power.
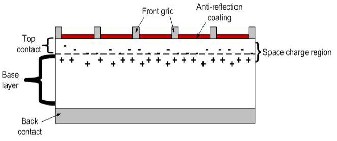
The cross-section of a PV cell is shown in Figure (13). The most common material used in PV cell manufacture is mono-crystalline or poly-crystalline silicon. Each cell is typically made of square or rectangular wafers of dimensions measuring about 10cm X 10cm X 0.3mm [5]. In the dark the PV cell's behavior is similar to that of a diode and the well known Shockley-Read equation can be used to model its behavior.
 q*V 

I  I o e  *K *T  1

Figure (13): Structure of a PV cell[5]

7.2-PV module

For the majority of applications multiple solar cells
need to be connected in series or in parallel to produce enough voltage and power. Individual cells are usually connected into a series string of cells (typically 36 or 72) to achieve the desired output voltage. The complete assembly is usually referred to as a module and manufacturers basically sell modules to customers. The modules serves another function of protecting individual cells from water, dust etc. as the solar cells are placed
into an encapsulation of single or double at glasses.
 
  Within a module the different cells are connected

where: Io is the reverse saturation current of diode

(A),

q is the electron charge (1.602×10-19 C),

Vd is the voltage across the diode (V),

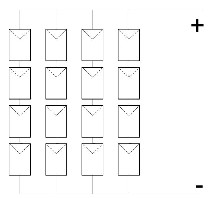
electrically in series or in parallel although most modules have a series connection. Figure (14) shows a typical connection of how 36 cells are connected in series. In a series connection the same current flows through all the

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 11

ISSN 2229-5518

cells and the voltage at the module terminals is the sum of the individual voltages of each cell. It is therefore, very critical for the cells to be well matched in the series string so that all cells operate at the maximum power points. When modules are connected in parallel the current will be the sum of the individual cell currents and the output voltage will equal that of a single cell.
though that it becomes very difficult to replace the diode if it fails.

7.4-Standalone systems

Historically the first cost-effective application of
photovoltaics were stand-alone systems especially in remote areas where it was not feasible or prudent to connect to the main utility grid. Solar power is also seeing growth in small applications, the majority of which, are portable electronic goods such as calculators, watches, ashlights just to name a few. A stand-alone system is shown in Figure (16).
In the developing world stand-alone systems will go a long way in rural electrication. They can also be used for mobile equipment and communication systems and water pumping systems. Typically a stand-alone system comprises of the solar module(s), some power conditioning and control units (converters: dc-dc, inverter), some storage elements and the load.

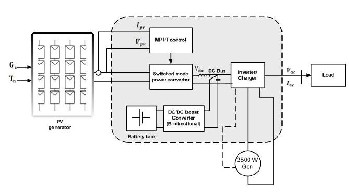
Figure (16): Stand-alone PV system [5,6]

7.3-PV array

An array is a structure that consists of a number of PV
modules, mounted on the same plane with electrical connections to provide enough electrical power for a
given application. Arrays range in power capacity from a
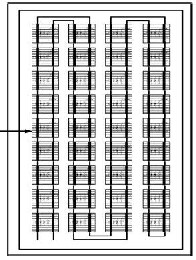
few hundred watts to hundreds of kilowatts. The connection of modules in an array is similar to the connection of cells in a single module. To increase the voltage, modules are connected in series and to increase the current they are connected in parallel. Matching is again very important for the overall performance of the array. The structure of an array is shown in figure (15), which has 4 parallel connections of 4 module strings connected in series.

For an array to perform well all the modules must not be shaded otherwise it will act as a load resulting in heat that may cause damage. Bypass diodes are usually used to avoid damage although they result in further increase in cost. Integration of bypass diodes in some large modules during manufacturing is not uncommon and reduces the extra wiring required. It must be pointed out

Figure (17): Hybrid PV system[5].

7.5-Hybrid systems

In cases where it is not feasible economically or
practically to supply the requisite energy from PV modules other means are used. In most cases the PV system is used in conjunction with a Diesel generator. Such a hybrid system ensures that energy demands are met while fully utilizing the PV supply. A typical hybrid system is shown in Figure (17).

7.6-Grid connected PV systems (fig.(18))

Grid connected PV systems provides a person or business
the opportunity to be self sufficient in terms of energy while protecting the environment. Installed grid

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 12

ISSN 2229-5518

connected systems have increased considerably over the recent years with Germany alone boasting close to (1
GW) of installed PV power by the year 2004 [5]. More installations are going to be witnessed as governments are putting in place more legislations to promote the use of renewable energy and the cost of PV systems continues to reduce. Most technical issues with regards to connection of PV systems to the utility grid have been solved; IEEE adopted standard 929-2000 in 2000 [9]. In the standard the integration of PV systems to electricity networks is covered in two main categories: safety and power quality. The IEEE Std 929 states that the limits on the total harmonic distortion caused by the PV system at the point of common coupling (PCC) must comply with Clause 10 of IEEE Std 519-1992. These limits are shown in Table (6). These limits apply to six pulse converters and for general distortion situations for pulse numbers greater than six a conversion formula is given [5].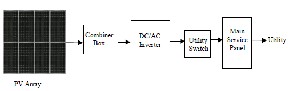

With regards to safety, an important issue that has been extensively studied is the issue of islanding whereby the inverter is supposed to automatically shut down if the source of power is disconnected from the network. If this does not happen the safety of the utility staff and public will be critically compromised. Another issue is Radio Frequency Suppression which demands proper filtering and shielding.

Figure (18-a) Simple PV System Diagram

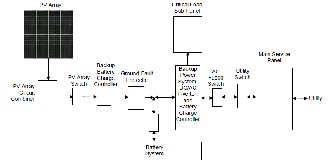
Figure (18-b): Grid-Interactive Only (No Battery Backup)

Figure (18-c): Grid-Interactive Only with Battery Backup

Figure (18): Grid connected PV system [5]

Table (6): Distortion limits as recommended in IEEE Std

519-1992 for six-pulse converters [5]

7.7-PV Module power sizes

There are different sizes of PV module commercially available (typically sized from 60W to 170W). Usually, a number of PV modules are combined as an array to meet different energy demands. For example, a typical small- scale desalination plant requires a few thousand watts of power [1]. The size of system selected for the proposed system is 150W, which is commonly used in small water pumping systems for cattle grazing in rural areas of the United States. The power electronics lab located in the building 20, room 104, has three BP SX 150S multi- crystalline PV modules. Each module provides a maximum power of 150W [1],

7.8-Definition of maximum Power Point

Tracker

The maximum power point tracker (MPPT) is now
prevalent in grid-tied PV power systems and is becoming more popular in stand-alone systems. It should not be confused with sun trackers, mechanical devices that rotate and/or tilt PV modules in the direction of sun. MPPT is a power electronic device interconnecting a PV power source and a load, maximizes the power output from a PV module or array with varying operating conditions, and therefore maximizes the system efficiency. MPPT is made up with a switch-mode DCDC converter and a controller. For grid-tied systems, a switch-mode inverter sometimes fills the role of MPPT. Otherwise, it is combined with a DC-DC converter that performs the MPPT function.

In addition to MPPT, the system could also employ a sun tracker. According to the data in reference [5,13,24], the single-axis sun tracker can collect about 40% more energy than a seasonally optimized fixed-axis collector in summer in a dry climate such as Albuquerque, New Mexico. In winter, however, it can gain only 20% more energy. In a climate with more water vapor in the atmosphere such as Seattle, Washington, the effect of sun tracker is smaller because a larger fraction of solar irradiation is diffuse. It collects 30% more energy in summer, but the gain is less than 10% in winter. The two-axis tracker is only a few percent better than the single-axis version. Sun tracking enables the system to meet energy demand with smaller PV modules, but it increases the cost and complexity of system. Since it is made of moving parts, there is also a higher chance of failure. Therefore, in this simple system, the sun tracker is not implemented. A detailed discussion on MPPT appears in the next sections.

7.9- Photovoltaic energy (PV)

Photovoltaic (PV) cells are semi-conductor devices,
which converts sunlight energy directly to electrical energy. Conventional photovoltaic cells are made of crystalline silicon that has atoms arranged in a three dimensional array, making it an efficient semiconductor. Although, this material is most commonly used for generation of electricity, it also has associated drawbacks, such as high material costs for silicon, costly processes for purifying silicon and manufacturing wafer, additional

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 13

ISSN 2229-5518

processes for assembly of modules and the bulky and rigid nature of the photovoltaic panels.
Becquerel had discovered the photovoltaic effect in selenium in 1839. The conversion efficiency of the new silicon cells developed in 1958 was 11% although the cost was prohibitively high ($1000/W) [1]. The first practical application of solar cells was in space, where cost was not a barrier as no other source of power is available.
PV equipment has no moving parts and as a result requires minimal maintenance and has a long life. It generates electricity without producing emissions of greenhouse or any other gases, and its operation is virtually silent.
A PV cell consists of two or more thin layers of semi- conducting material, most commonly silicon. When the
silicon is exposed to light, electrical charges are generated and this can be conducted away by metal
contacts as direct current (DC). The electrical output from a single cell is small, so multiple cells are connected together and encapsulated (usually glass covered) to form
a module (also called a panel).
The PV panel is the principle building block of a PV system and any number of panels can be connected together to give the desired electrical output. This modular structure is a considerable advantage of the PV system, where further panels can be added to an existing system as required.
Photovoltaic (PV) cells are made of various semiconductors, which are materials that are only moderately good conductors of electricity. The materials most commonly used are silicon (Si) and compounds of cadmium sulphide (CdS), cuprous sulphide (Cu2S), and gallium arsenide (GaAs). These cells are packed into modules which produce a specific voltage and current when illuminated. PV modules can be connected in series or in parallel to produce larger voltages or currents. Photovoltaic systems can be used independently or in conjunction with other electrical power sources. Applications powered by PV systems include communications (both on earth and in space), remote power, remote monitoring, lighting, water pumping and battery charging. The global installed capacity of photovoltaic at the end of 2002 was near 2 GWp [1].
PV applications are: either Stand-alone applications or
Grid-connected systems. Standalone PV systems are used in areas that are not easily accessible or have no access to main electricity. A standalone system is independent of the electricity grid, with the energy produced normally being stored in batteries. A typical stand-alone system would consist of PV module or modules, batteries and charge controller. An inverter may also be included in the system to convert the direct current (DC) generated by the PV modules to alternating current (AC) required by normal appliances.
For grid-connected systems. Nowadays, it is usual practice to connect PV systems to the local electricity network. This means that during the day, the electricity generated by the PV system can either be used immediately (which is normal for systems installed in offices, other commercial buildings and industrial
applications), or can be sold to one of the electricity
supply companies (which is more common for domestic
systems, where the occupier may be out during the day). In the evening, when the solar system is unable to provide the electricity required, power can be bought back from the network. In effect, the grid is acting as an energy storage system, which means the PV system does not need to include battery storage.
For PV system configuration. The PV array consists of a number of individual photovoltaic modules connected together to give a suitable current and voltage output.
Common power modules have a rated power output of around 50–80 W each. As an example, a small system of 1.5–2 kWp may therefore comprise some 20–30 modules covering an area of around 15–25 m2, depending on the technology used and the orientation of the array with respect
to the sun.
Most power modules deliver direct current (DC) electricity at 12 volts (V), whereas most common household appliances and industrial processes operate with alternating current (AC) at 240 or 415 V (120 V in the United States).Therefore, an inverter is used to convert the low voltage DC to higher voltage AC. Numerous types of inverters are available, but not all are suitable for use when feeding power back into the mains supply.
Other components in a typical grid-connected PV system are the array mounting structure and the various cables and switches needed to ensure that the PV generator can be isolated.
Attractiveness of the PV technology is low maintenance, and no pollution, and has positioned PV to
be the preferred power technology for many remote
applications for both space and on the ground. Photovoltaic (PV) technology is expected to be a leading technology to solve the issues concerning the energy and the global environment due to several advantages of the PV system. The installed, unsubsidized costs, now coming close to $0.2/kWh in the best applications while average electric rates from utilities are less than
$0.1/kWh [1, 9]. Although, photovoltaic electricity is three to five times more expensive than other conventional grid power systems, PV is turning into a mainstream. The average cost for PV technology in 2006 was roughly $7–10 per peak watt installed [1]. On the other hand, the average module cost is about $4.34/W on November 2009 [1]. The lowest retail price for a multi- crystalline silicon solar module is $2.48 per watt from a US retailer. The lowest retail price for a monocrystalline silicon module is also $2.70 per watt, from an Asian retailer [9]. Sun Power Corporation, a leader in PV industry is currently offers PV modules at 18% peak efficiency. However, climatic effects such as dirt accumulation and temperature rise as well as aging, which causes a gradual increase of the device’s internal leakage conductance, and consequently lowers the efficiency.

7.10- Main PV Cell Types

The material that is widely used in the industry of PV
cells is silicon. Silicon can be found inside the sand in the form of silicon oxide (SiO2). Depending on the structure of the basic material from which PV cells are made and

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 14

ISSN 2229-5518

the particular way of their preparation, PV cells can mainly be categorized as follows, fig.(19) and table(9) [5,
13, 14,45]:
1. Mono-crystalline: The efficiency of a single crystal silicon cell varies between 13-16% and it is characterized by a high cost for its manufacture and has a dark blue color.
2- Poly-crystalline: Its efficiency varies between 10-14% and it is characterized by lower cost silicon which is used for its manufacture and has light blue color.
3- Amorphous (non crystalline) silicon: This type of photovoltaic cells achieves maximum efficiency not more than 10%. Production cost is much cheaper than what is for the previous two types. Its efficiency degrades with time.
4- Other types of PV cells use other materials or
compounds rather than silicon. Other innovative PV technologies use multi-junction, silicon spheres, or photo electrochemical in manufacturing the PV cells.

advantage of amorphous solar panels over the other two is that they are shadow protected. That means that the solar panel continues to charge while part of the solar panel cells is in a shadow. These work great on boats and other types of transportation [5, 13, and 15].

Fig.(19): Main types of PV cell[5,13,14,24].

Table(7): Module efficiencies and energy consumption[45].

7.11- Thin-film photovoltaic

As mentioned above, PV thin film technology are
usually divided into mono-crystalline, multi-crystalline silicon and amorphous silicon cells [5, 13, 14, 24] .

Mono-crystalline silicon cells are made from very pure mono-crystalline silicon. The silicon has a single and continuous crystal lattice structure with almost no defects or impurities. The principle advantage of mono- crystalline cells is their high efficiency, typically around

15%, although the manufacturing process required to
produce mono-crystalline silicon is complicated, resulting in slightly higher costs than other technologies.

Multi-crystalline silicon cells are produced using numerous grains of mono-crystalline silicon. In the manufacturing process, molten polycrystalline silicon is cast into ingots; these ingots are then cut into very thin wafers and assembled into complete cells. Due to the simpler manufacturing process, multi-crystalline cells are cheaper to produce than mono-crystalline ones. However, they tend to be slightly less efficient, with average efficiencies of around 12%.

Amorphous silicon cells are composed of silicon atoms in a thin homogenous layer rather than a crystal structure. Amorphous silicon absorbs light more effectively than crystalline silicon, so the cells can be thinner. For this reason, amorphous silicon is also known

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 15

ISSN 2229-5518

as a ‘thin film’ PV technology. Amorphous silicon can be deposited on a wide range of substrates, both rigid and flexible, which makes it ideal for curved surfaces and
‘fold-away’ modules. Amorphous cells are, however, less
efficient than crystalline based cells, with typical efficiencies of around 6%, but they are easier and therefore cheaper to produce. Their low cost makes them ideally suited for many applications, where high efficiency is not required and low cost is important. Amorphous silicon (a-Si) is a glassy alloy of silicon and hydrogen (about 10%). Several properties make it an attractive material for thin-film solar cells:
1.Silicon is abundant and environmentally safe.
2..Amorphous silicon absorbs sunlight extremely well, so that only a very thin active solar cell layer is required (about 1 mm as compared to 100 mm or so for crystalline solar cells), thus greatly reducing solar-cell material requirements.
3. Thin films of a-Si can be deposited directly on inexpensive support materials such as glass, sheet steel, or plastic foil.
Other thin films which are promising materials such as cadmium telluride (CdTe) and copper indium diselenide (Cu In Se2) are now being used for PV modules. The attraction of these technologies is that they can be manufactured by relatively inexpensive industrial processes, in comparison to crystalline silicon
technologies, yet they typically offer higher module efficiencies than amorphous silicon.
Photovoltaic panels or modules are designed for outdoor use in such a harsh conditions as marine, tropic, arctic, and desert environments. The choice of the photovoltaically active material can have important effects on system design and performance. Both the composition of the material and its atomic structure are influential.
The atomic structure of a PV cell can be single-crystal (mono-crystalline), multi-crystalline, or amorphous. The most commonly produced PV material is crystalline silicon, either polycrystalline or in single-crystals.
A module is a collection of PV cells that protects the cells and provides a usable operating voltage. PV cells can be fragile and susceptible to corrosion by humidity or fingerprints and can have delicate wire leads. Also, the operating voltage of a single PV cell is less than 1 V, making it unusable for many applications. Depending on the manufacturer and the type of PV material, modules have different appearances and performance characteristics. Also, modules may be designed for specific conditions, such as hot and humid climates. Nowadays, the panels come in a variety of shapes like roof-tiles made from amorphous silicon solar cells.
Usually, the cells are series-connected to other cells to produce an operating voltage around 14–16 V. These strings of cells are then encapsulated with a polymer, a front glass cover, and a back material. Also, a junction box is attached at the back of the module for convenient wiring to other modules or other electrical equipment.
Cells made of amorphous silicon, cadmium telluride, or copper indium diselenide are manufactured on large pieces of material that become either the front or the back of the module. A large area of PV material is divided into
smaller cells by scribing or cutting the material into electrically isolated cells.
It is evident that since the past 15–20 years various thin-film technologies have been under development for reducing the amount of light absorbing material required in producing a solar cell. Since silicon is the key contributor to the cost of PV technology, using less silicon will have a considerable effect on the cost reduction of the PV technology.
Conversion efficiency is one major metric for solar material, which represents how much of the sun’s energy the material can convert into electricity. Today, the laboratory efficiency of the Amorphous Silicon (a-Si) is
12.3%, Cadmium Telluride (CdTe) is 16.5% and Copper
Indium Gallium Selenide (CIGS) is 19.9% [5,13,14,24].
Advantages of Thin Film Technologies over Conventional Crystalline Silicon are lower cost of production than conventional silicon processes, lower
production facility cost per watt, use of far less material, as little as 1/500th the amount used in standard silicon cells, and lower energy payback. It also produces more useable power per rated watt, provides superior performance in hot and overcast climates, has the ability to be attractively integrated into buildings and produces the lowest cost of power. The thin-film module manufacturing cost decreased to 98 cents per watt, breaking the $1 per watt price barrier [22, 23].Although, thin-film cells are not as efficient as conventional crystalline silicon-especially as they are not used in tandem devices, it is believed that thin-film will be a dominant PV technology in the future. Many also believe
that, the likelihood of significant reduction of module cost has many opportunities to increase the efficiency that surely will reduce the overall cost of thin-film technology.

8-Photovaltaic technology [8, 14, 16-18, 25-26]

8.1 Photovoltaic Cell

Photons of light with energy higher than the band-gap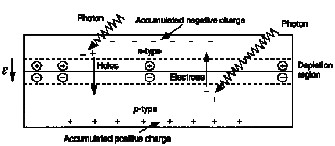

energy of PV material can make electrons in the material break free from atoms that hold them and create hole- electron pairs, as shown in Figure (35). These electrons, however, will soon fall back into holes causing charge carriers to disappear. If a nearby electric field is provided, those in the conduction band can be continuously swept away from holes toward a metallic contact where they will emerge as an electric current. The electric field within the semiconductor itself at the junction between two regions of crystals of different type, called a p-n junction [5,13,14,24].

Figure (35): Illustration of the p-n junction of PV cell

[5,13,14,24]

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 16

ISSN 2229-5518

K T  I 

Voc  B ln L  1

e  Io 

Figure (36): Illustrated side view of solar cell and the conducting current [5,13,14,24]

The PV cell has electrical contacts on its top and
bottom to capture the electrons, as shown in Figure (36). When the PV cell delivers power to the load, the electrons flow out of the n-side into the connecting wire, through the load, and back to the p-side where they recombine with holes [13]. Note that conventional current flows in the opposite direction from electrons.

8.2-Background:

A-Nature of Light:

Light is a form of the radiant energy, which is propagated through space or matter as electromagnetic
waves. Light differs form other kinds of electromagnetic radiation such as radio waves, heat ,and X- rays only in wavelength or frequency . The Sunlight is composed of packets of energy which is known as photons. These
photons contain various amounts of energy
corresponding to the different wavelengths of light. When photons strike a semiconductor, they may be reflected or absorbed, or they may pass right through. When a photon is absorbed, its energy is transferred to an electron in the semiconductor. The electron with its newfound energy will be able to escape from its normal position associated with that semiconductor to become part of the current in an electrical circuit [5,13,14,24].

b-Photovoltaic Effect:

The photovoltaic (or PV) effect is the basic physical process through which sunlight converts into electricity.
The word photovoltaic is a joining of two words Photo, meaning light, and voltaic, meaning electricity. And this is the phenomenon by which certain materials, properly processed and fabricated into suitable devices; generate a
voltage when they are exposed to light. The photovoltaic

cell or self generating photocell is one that generates an output voltage in proportion to the intensity of incident light.
And the voltage is given by:

V  K BT  I  I L 

ln  1

e  Io 

There are many important quantities we can determine,
firstly, the short-circuit current (ΙSC) which is, by setting
V =0, in Eq (2-2) equal to the light generated current (IL
).

Secondly, the open - circuit voltage (VOC) which can obtain by setting I =0 in Eq. (2-3):
At high intensities of light the open circuit voltage can approach the semiconductor band gap. In the case of Si solar cells for solar illumination (without atmospheric absorption) the value of Voc is roughly 0.7 eV.
A plot of the current in the solar cell as a function of

the voltage provides the curve shown in Fig. (37). In general, the electrical power delivered to the load is given by:
The maximum power Pm is delivered at voltage and current values of Vm and Im as shown in Fig. (37).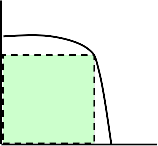

I

Isc

Im

Maximum Power Rectangle (Pm)

Vm Voc V

Figure (37): The I.V characteristics of the solar cell[13].

The open circuit voltage is Voc and the short circuit current is the maximum power is Isc delivered at the Rectangle shown in Figure (37). [14, 15]

8.3- Equivalent Circuit of Solar Cell:

An ideal solar cell may be modeled by a current source

in parallel with a diode. In practice no solar cell is ideal, so a shunt resistance and a series resistance component are added to the model. The result is the equivalent circuit of a solar cell shown in. fig. (38). [5,13,14,24]

Figure (38): Equivalent circuit of the solar cell [13].

8.3-Construction and operation

- Photovoltaic construction

A solar cell is considered the basic part in the
photovoltaic system; it is a device that converts light energy into electrical energy by the photovoltaic effect. Solar cells are often electrically connected and encapsulated as a module. PV modules often have a sheet of glass on the front (sun up) side, allowing light to pass while protecting the semiconductor wafers from the elements (rain, hail, etc.). Solar cells are also usually connected in series in modules, creating an additive voltage. Connecting cells in parallel will yield a higher current. Modules are then interconnected, in series or parallel, or both, to create an array with the desired peak DC voltage and current.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 17

ISSN 2229-5518

PV cells consist basically of a junction between two thin layers of semi conducting materials, known as p (positive) type semiconductors and n (negative) type semiconductors. The p-type semiconductor is created when some of the atoms of the crystalline silicon are replaced by atoms with lower valence like boron which causes the material to have a deficit of free electrons. The n-type semiconductor is created when some of their atoms of the crystalline silicon are replaced by atoms of another material which has higher valence band like phosphorus in such a way that the material has a surplus of free electrons. The photovoltaic cell consists of 6 different layers of materials as shown in figure (39).

Figure (39): Silicon PV cell construction[45]

8.4- Operation and Characteristics of PV or

Solar Cells

-Principle of Operation of Solar Cell

An array of solar cells converts solar energy into a usable

amount of direct current (DC) electricity. The solar panels are mainly made out of semiconductor material and silicon being the most abundantly used semiconductor. Solar cells are connected in series to increase the output voltage. Similarly, the cells in parallel will yield a higher current. Series connected cells are
called as PV modules and the interconnection series and parallel combination of solar cells is an array.
The operation of solar cells may be described from a PN junction where there are diffusion currents and drift currents for the direct and reverse polarization, respectively. Usually, the cells operate in reverse direction so that the current drift is desirable. When the PN junction is exposed to light, photons with energy greater than the gap of energy are absorbed, causing the emergence of electron-hole pairs. These carriers are separated under the influence of electric fields within the junction, creating a current that is proportional to the incidence of solar irradiation [5,13,14,24].

- Characteristics of Solar Cell:

Solar cells naturally exhibit a nonlinear I-V and P-V
characteristics which vary with the solar irradiation and cell temperature. The typical I-V and P-V characteristics of solar cell are shown in figure (40).

-Variation of PV characteristics with temperature

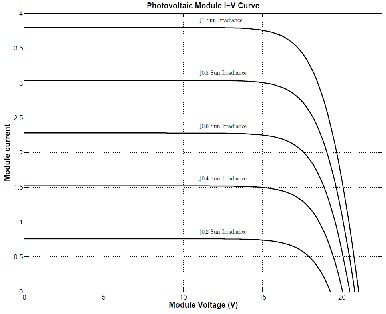
The performance of a photovoltaic module at a constant level of irradiance (1000 W/m2 or 1 Sun in this case) is depicted in Figure (41). There is a clear reduction in the open circuit voltage as the temperature increases.
Figure (41) provides a clear view on how the curves vary with temperature and constitutes a typical set of curves that are displayed on a manufacturer's datasheet. There is significant reduction in the power output of the photovoltaic system as cell temperature increases. This relationship is clearly depicted in Figure (42) where the power is plotted as a function of voltage for 4 different temperatures.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012 18

ISSN 2229-5518

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

19

ISSN 2229-5518

-Variation of PV characteristics with irradiance

To show the effect of irradiance on the
performance of a module the temperature is kept fixed at 25 0C and the values of irradiance are changed to different values. The variation of the current-voltage characteristics with irradiance are shown in Figure (43). It is quite clear that irradiance has a major effect on the short circuit current and indeed the relationship between irradiance and the short circuit current
is a linear one. Power was also calculated at different levels of irradiation as shown in 6.5. To obtain the maximum possible output from the photovoltaic module, it has to operate at the voltage corresponding to maximum power as shown by the dotted lines.

9-Photovoltaic Electrical System:

An individual solar cell generates a low
voltage, approx 0.5V, and only DC current, which is not enough for many applications. Therefore, solar cells must be used through an electrical system known as Photovoltaic electrical Systems, or PV Systems, for short. PV Systems have two general types of electrical designs; off-grid and grid-connected systems. Off-grid, or Stand-alone, systems are those which use photovoltaic technology only, and they are not connected to a utility grid. Such systems need a battery backup. On the other hands, grid-tied systems interact with the utility power grid and have no battery backup capability.
Both types need many components to make the entire system fully functional to supply the needed electricity. These components can be divided into essential and optional ones. [13,14,24]

9.1- The Essential Components:

i) PV Modules and Arrays:

Solar cells, composed of semiconductor
materials such as silicon are the basic of building of PV technologies. An individual PV cell typically produces between 1 and 2 Watts, hardly enough to meet household needs. To increase the power output, a number of cells are connected in series or parallel to form larger PV modules. The module is the smallest commercially available unit for power applications. PV modules range in power output from about 6 watts to about 300 watts with supposed output voltages from 6 to 90 volts. Connecting modules together in series will increase the output voltage, while parallel connection increases the output current. These groups of modules form PV panels or arrays. System designers can create PV arrays that have power outputs of 15kW or more. A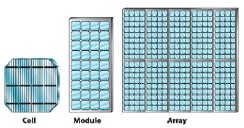

typical PV module consists of a protective weatherproof enclosure for the semiconductor materials and the electric wiring, as it is shown in Fig (44). [13,14,24]

Figure (44): Diagram that shows how individual cells make up a module. An array consists of

sets of modules (from the National Renewable

Energy Laboratory, Golden, CO).

ii) Inverters:

PV cells produce direct current DC, rather
than alternating current AC, which is required to run most common household appliances and electronic devices. The inverter converts the DC power produced by the PV array into AC power consistent with the voltage and power quality requirements of the utility grid, and automatically stops supplying power to the grid when the utility grid is not energized. The inverter must be carefully selected to insure proper operation with other system components, for most net metering applications inverters will range in size from
100 Watts, small inverters, to 4kW, large inverters. Large inverters typically contain built in battery chargers. This allows the inverter to operate as a battery charger when power is available from another AC source such as a generator.
There are two classes of inverters. Sine wave inverters supply clean, utility-grade power. Modified sine wave inverters supply a stepped sine wave output. This power is not as clean as pure sine wave inverters; however, they can operate well in most stand-alone applications and are less expensive than pure sine wave inverters. [13.14, 24]

iii) Batteries (off-grid):

Batteries are an essential component for off-
grid or emergency backup power systems. Several batteries linked together comprise a battery "bank", which collects and stores energy produced by the PV array for periods. Several factors can be used to help determine the size of the battery bank. These include the electric load, the duration of required reserve power, and the availability of a source of backup power, grid or generator. A good quality, lead-acid battery bank will last from

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

20

ISSN 2229-5518

500 to 1,000 charge-discharge cycles depending on depth of discharge and attention to maintenance considerations. Other types of batteries are available such as Nickel Cadmium. These batteries are longer lasting, but quite a bit more expensive than lead acid batteries. A battery box is needed to enclose the battery bank. The battery box must provide adequate ventilation of explosive hydrogen gas that produced during battery charging to the outside. This includes careful attention to charge and discharge levels, periodic watering, and inspection of cables and connections for tightness and corrosion. [13.14, 24]

iv) Wiring:

Connecting PV panels to the household
requires properly sized wiring, installed according to code standards. All systems also require fuses for protection of people and equipment. Interconnection requirements in Vermont include a utility accessible, lockable, load break rated, visible break disconnect switch for all grid connected PV installations. [13.14, 24]

v) Charge Controller:

A charge controller regulates the amount of

energy flowing from the PV array to the batteries. This is essential to avoid the damaging situation of overcharging the batteries. Figure (45) shows how this controller works. [13, 14, 24]

Figure (45): Diagram of stand-alone PV

system[13,14,24].

9.2-The Optional Components:

i) Metering:

Grid connected households will most commonly use a single meter set up, whereby
the utility meter registers the net difference between the household's load and PV system output. When the PV output is greater than the house's consumption, the meter will spin
backwards. If the sun is shining, and the
is not shining, the utility meter operates as usual in a non-solar house. The single meter set up is attractive because there is no additional cost for PV metering. However, it is difficult to know how much solar electricity is actually generated each month. [13, 14, 24]

ii) Generator:

Some off grid home owners need to install a generator to supplement the PV system during
cloudy periods, or for when high-power equipment such as washing machines, water pumps or power tools are being used. [13, 14,

24]

iii) Concentrating Photovoltaic (CPV):

To concentrating photovoltaic systems use a

large area of lenses or mirrors to focus sunlight on a small area of photovoltaic cells. These systems use single or dual-axis tracking to improve performance as it is shown in figure (46). The primary attraction of CPV systems is their reduced usage of semiconductor material which is expensive and currently in short supply. Additionally, increasing the concentration ratio improves the performance of general photovoltaic materials and also allows for the use of high performance materials such as gallium arsenide. Despite the advantages of CPV technologies their application has been limited by the costs of focusing, tracking and cooling equipment. The sunflower is a CPV system currently in development. [13,14,24]

Figure (46): A parabolic solar collector concentrating the sun's rays on The solar cells (Solar Stirling Engine)

10-Factors Affecting PV Output

10.1-Standard Test Conditions

Solar modules produce dc electricity. The dc
output of solar modules is rated by manufacturers under Standard Test Conditions (STC). These conditions are easily recreated in a factory, and allow for consistent comparisons of products, but need to be modified to estimate output under common outdoor operating conditions. STC conditions are: solar

o

household load is greater than the PV output, then the meter will spin forward, but more
cell temperature = 25
(intensity) = 1000 W/m2
C; solar irradiance
(often referred to as
slowly than it would if there was no contribution of solar electricity. When the sun
peak sunlight intensity, comparable to clear
summer noon time intensity); and solar

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

21

ISSN 2229-5518

spectrum as filtered by passing through 1.5 thickness of atmosphere (ASTM Standard Spectrum). A manufacturer may rate a particular solar module output at 100 Watts of power under STC, and call the product a “100- watt solar module.” This module will often have a production tolerance of +/-5% of the rating, which means that the module can produce 95 Watts and still be called a “100- watt module.” To be conservative, it is best to use the low end of the power output spectrum as a starting point (95 Watts for a 100-watt module).

10.2-Factors Affecting Output

A-Temperature [13,14,24]

Module output power reduces as module
temperature increases. When operating on a roof, a solar module will heat up substantially, reaching inner temperatures of 50-75 oC. For crystalline modules, a typical temperature reduction factor recommended by the CEC is
89% or 0.89. So the “100-watt” module will
typically operate at about 85 Watts (95 Watts x
0.89 = 85 Watts) in the middle of a spring or fall day, under full sunlight conditions.

B-Dirt and dust

Dirt and dust can accumulate on the solar
module surface, blocking some of the sunlight and reducing output. Much of California has a rainy season and a dry season. Although typical dirt and dust is cleaned off during every rainy season, it is more realistic to estimate system output taking into account the reduction due to dust buildup in the dry season. A typical annual dust reduction factor to use is
93% or 0.93. So the “100-watt module,” operating with some accumulated dust may operate on average at about 79 Watts (85 Watts x 0.93 = 79 Watts).

c-Mismatch and wiring losses

The maximum power output of the total PV
array is always less than the sum of the maximum output of the individual modules. This difference is a result of slight inconsistencies in performance from one module to the next and is called module
mismatch and amounts to at least a 2% loss in system power. Power is also lost to resistance
in the system wiring. These losses should be kept to a minimum but it is difficult to keep these losses below 3% for the system. A reasonable reduction factor for these losses is
95% or 0.95 due to Dc to ac conversion losses. The dc power generated by the solar module
must be converted into common household ac power using an inverter. Some power is lost in the conversion process, and there are
additional losses in the wires from the rooftop array down to the inverter and out to the house panel. Modern inverters commonly used in residential PV power systems have peak efficiencies of 92-94% indicated by their manufacturers, but these again are given below:

d-Sun angle and house orientation

During the course of a day, the angle of
sunlight striking the solar module will change, which will affect tm the power output. The output from the “100-watt module” will rise from zero gradually during dawn hours, and increase with the sun angle to its peak output at midday, and then gradually decrease into the afternoon and back down to zero at night. While this variation is due in part to the changing intensity of the sun, the changing sun angle (relative to the modules) also has an effect The pitch of the roof will affect the sun angle on the module surface, as will the East- West orientation of the roof. These effects are summarized in Table (7), which shows that an array on a 7:12-pitch roof facing due South in Southern California gives, for example, the greatest output (correction factor of 1.00), while an East facing roof at that same pitch would yield about 84% of the annual energy of the South facing roof (a correction factor of
0.84 from Table (8).
Table (8) is intended to give a conservative estimate of the annual energy expected from a typical PV system, taking into account the various factors discussed above.
These values are for annual kWh produced from a 1-kilowatt (1kW) STC DC array, as a simple and easy guide. If the system includes battery backup the output may be reduced further by 6-10% due to battery effects.
Example: A 4 kWSTC solar array (as specified under STC conditions) located in the Los Angeles area at a 4:12 pitch and facing southeast should produce at least 5343 kWh of electric energy annually (1406 kWh/kW x 0.95 x 4 kW = 5343 kWh). The typical residential customer in that area uses about 7300 kWh annually1, meaning such a PV system could produce at least 75% of the total energy needed by such a typical home. And if energy efficiency measures were taken by the owner to reduce the overall electrical consumption of the home, the percentage could approach
100%. Note that the low end of the range was used to calculate the actual savings. It is wise to be conservative when making performance claims. Net metering has recently been extended to time-of-use customers yielding a potential additional value of 20-30% for the PV electricity generated by the system. With

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

22

ISSN 2229-5518

this net time-of-use metering, the homeowner would cover almost their entire electric bill and only have to pay the monthly metering charge.

Table (8): Orientation Factors for Various Roof

Pitches and Directions

11- Solar Cell Limitation:

Solar cells have a lot of applications but they
are limited by three main factors; efficiency, cost, and Lifetime

11.1 Efficiency:

Solar cells are characterized by the percentage of the incident power that they
convert into electric power. This characteristic factor is called the power conversion efficiency or just efficiency. The efficiency is given by a percentage and it is depend on many factors. [33]

i) Energy Losses:

Light is composed of photons—or packets of
energy—that range in wavelength. The energy of photons can be expressed in term of
wavelength by the relation λhc/ Ε=. When

light strikes the surface of a solar cell, some photons are reflected and the other photons pass through the material, some are absorbed but only have enough energy to generate heat, and some have enough energy to exciting an electron from the valence band to the conduction band, leaving behind a positively charged hole. If these excited carriers can be separated before they spontaneously recombine, voltage and current can be derived, hence power can be provided to a load. . [34,37]

Figure (32): Processes through which energy can be lost in the solar cell

In stander solar cell, there are four processes through which energy can be lost. Namely;
1) If the light energy is lower than the semiconductor band gap simply passes through unutilized, which represents a significant loss. . [13,14,24]
2) If an electron is excited to the conduction band by a photon with energy greater than the bandgap, it will lose energy as heat (thermalization of photogenerated carriers) until the energy of the electron is reduced to the bandgap energy, (see figure (32), case.1). [13,14,24]
3) When N and P-type silicon come into contact, they create their own electric field. This electric field is created when the electrons on the N-type silicon close-by fall into the holes in the P-type silicon. The result is a barrier between the positive and negative sides, called diode, which allows electrons to travel one way. The barrier is called a diode. The diode allows electrons to travel from the P- type silicon to the N-type silicon, but not the other way around (figure (32), cases 2 & 3) [13,14,24]
4) An electron in its excited state will spontaneously return to its ground state, and in doing so it will release energy as heat or light. This is known as recombination of the photoexcited electron-hole pairs (figure (32), case 4). [13,14,24]

ii) Natural electrical Resistance:

The natural resistance to electron flow in a cell decreases cell efficiency. These losses
control in three places: in the bulk of the primary solar material, in the thin top layer typical of many devices, and at the interface
between the cell and the electrical contacts leading to an external circuit. [13,14,24]
Larger electrical contacts can minimize

electrical resistance. But covering a cell with large, opaque metallic contacts would block too much incident light. Typically, top-surface contacts are designed as grids, with many thin, conductive spread over the cell's surface as it shown in figure (33). The back-surface contact of the cell is simpler, it often being just a layer of metal. [13,14,24]

Figure (33): Front and rear contacts of the solar cell[1].

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

23

ISSN 2229-5518

iii) Temperature:

Solar cells work best at low temperatures, as
determined by their material properties. All cell materials lose efficiency as the operating temperature rises. Much of the light energy shining on cells becomes heat, so it is good to either match the cell material to the operation temperature or continually cool the cell. [13,
14,24]

iv) Reflections:

A cell's efficiency can be increased by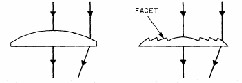

minimizing the amount of light reflected away from the cell's surface. For example, silicon reflects more than 30% of incident light. We can use antireflection (AR) technologies in the top layer of solar cell to optimize light absorption. A single AR layer will reduce reflection only at one wavelength. The best results with use multiple AR layers over a wider range of wavelengths.

Figure (34): Reducing reflection by texturing the top surface of the cell.

Another way to reduce reflection is to texture the top surface of the cell as shown in figure (34), which causes reflected light to strike a second surface before it can escape, thus increasing the probability of absorption. If the front surface is textured into pyramid shapes for antireflection, all incident light is bent so that it strikes the polished—but otherwise untreated—back surface of the cell at an angle. This texturing causes light to be reflected back and forth within the cell until it is completely absorbed. [13,14,24]

v) Light intensity:

The best result of solar cells electricity in the
daylight, whereas the result is not good at sunrise or sunset as a result of smallness of light intensity. A higher light intensity will be focused on the solar cells by the use of mirror and lens systems. [13]
Silicon as a semiconductor has many limitations. While the limit on conversion of sunlight to electricity is 95%, the theoretical upper limit for the standard single junction silicon solar cell is just 33% and the research or laboratory efficiency of these is close to
25% as a result of previous limitations. The theoretical efficiency rises to 40.8% under concentrated light. [24]

11.2 Cost:

Solar cells in commercial production today
are expensive; they cost around $6 per watt. To
understand what that means, consider this: If you install $600 worth of solar cells, you can power a typical light bulb for 25 years. That is about twice the cost of coal-based electricity.
Through various technological improvements, solar-cell prices have typically fallen by 5% to 6% a year, but no more, because cells are manufactured through complex processes similar to those employed for making PC processors and memory cards. [9, 20, 22]
The photovoltaic industry has achieved impressive improvements in solar cell efficiencies and significant cost reductions. Mostly photovoltaic cells today achieve efficiencies between 12 and 20 percent, well above what they were just 15 years ago. The price of photovoltaic panels has declined from
$100/watt in the 1970s to the current price of approximately $3 /watt. The global photovoltaic industry is expanding rapidly; global manufacturing of solar cells stood at 58 megawatts per year in 1992 and has risen to over 1,600 megawatts per year in 2005 - an increase of almost 30% per annum over the past 15 years. Analysts believe that the photovoltaic industry will continue to see impressive gains in efficiencies and cost reductions.
In recent years, most solar production has been going to Europe and Asia, even from US- based manufacturing facilities. Countries like Germany have had government motivation programs that have made the installation of solar systems attractive. In the US, some states have instituted financial motivations that have played an important role in starting to boost the use of solar electricity in the US.
The price of electricity produced from solar cells is still significantly more expensive than it is from fossil fuels like coal and oil, especially when environmental costs are not considered. Photovoltaics can be cost-
competitive for utility companies today,
especially in areas where photovoltaic installations can defer or avoid costly upgrades to the transmission and distribution system. [9,20,22]

11.3 Lifetime:

Solar cells lifetime depends on some factors
such as temperature, materials and the recombination rate that occurs inside the junction. It is found that lifetime slowly increases with temperature over the range of
10 to 80 C under constant irradiance. On the other hands, lifetime decreases with the recombination that occurs inside the solar cell. [9]

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

24

ISSN 2229-5518

Modules from crystalline cells have a lifetime of over twenty years, while thin-film modules will last at least ten years. [9]

12-Components sizing of PV system

12.1 PV Panel Sizing [13, 45]

where: Tamb: ambient temperature, 0C, G: solar radiation, W/m2,
NOCT:normal operating cell temperature, which is defind as the cell temperature when
the module operates under the following conditions at open circuit: (solar radiation

2

The total peak power of the PV generator
=800 W/m
, spectral distribution= air

o

required to supply certain load depends on load, solar radiation, ambient temperature, power temperature coefficient, efficiencies of solar charger regulator and inverter and on the safety factor taken into account to compensate for losses and temperature effect. This total peak power is obtained as follows:
Where EL is the daily energy consumption in kWh, PSH is the peak sun hours (in KSA PSH = 12) and as a figure it represents the
mass(AM1.5), ambient temperature 20C ,
wind speed >1m/s.
The following equation can be used to calculate Tc approximately if NOCT is not given by the manufacturer [13,45]:

Tc  Tamb  0.0256 * G

b-Solar radiation effect:

Increasing the solar radiation increases in the same proportion the short circuit current. The
following equation illustrates the effect of variation of radiation on the short circuit current:
yearly average of daily solar radiation intensity

I sc

@ G  I sc
@(1000w / m2 ) * (G /1000)
on horizontal surface in (kWh/m2 –day), ηPVR ,
ηV are efficiencies of solar charger regulator and inverter and SF is the safety factor [45].
The output power of the PV panel taking into consideration the solar radiation variation and temperature variation effects is given below:

Pout pv  Pr  pv * (G / Gref ) * 1  KT (Tc  Tref )

Where, Pout-pv : output power from the PV cell, Pr-pv: rated power at reference conditions (STC)
G : solar radiation in W/m2.,
Gref: Solar radiation at reference condition
(1000 W/m2),
Tc : cell temperature in 0K,
Tref: cell temperature at reference condition(20

0C),

KT: temperature coefficient of the max. Power (KT=-3.7*10-3 /10C for mono and poly crystalline Si).
The two most important effects that must be considered are due to variable temperature and solar radiation. The effect of these two parameters must be taken into account while sizing the PV system, and can be calculated as follows:

a-Effect of cell temperature:

this is an important effect on the power output
from the cell.This effect appears on the output voltage of the cell, where the voltage decreases as temperature increases. This decrease for silicon cell is approximately 2.3mV/ 1 0C increase in the cell temperature. The solar cell temperature can be found by the following equation[ 45]:
Where, G in w/m2.

12.2 Battery Bank Modeling and

Sizing

The output power from the wind turbine
varies with wind speed variations through the day. Also the maximum power output of the PV generator varies according to variations in solar radiation and temperature. So the PV generator and the wind turbine may not be able to meet the load demands at all times. A battery between the DC bus of the hybrid system and the load will compensate and act as a power supply during these times.
Excess energy during times when the output power from the wind turbine and the PV generator exceed the load requirement is stored in the battery to supply load at times when the wind turbine and the PV generator are not able to supply load.
The two main types of batteries used in hybrid systems are nickel-cadmium and lead- acid . Nickel-cadmium batteries are restricted in use for few systems due to higher cost , lower energy efficiency and limited upper operating temperature. Lead-acid batteries is still the most common type for the hybrid systems [13,45] .

- Lead acid battery construction and performance

A lead acid battery in its basic construction
is made of more than one electrochemical cells interconnected in such a way to provide the required voltage and current. Lead acid battery is constructed of two electrodes, the positive
  one consists of lead dioxide PbO2 and the

Tc  Tamb

  NOCT  20  * G
 800 
negative consists of pure lead (Pb). The empty space between the two electrodes is filled with

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

25

ISSN 2229-5518

diluted sulphuric acid ( H2SO4 ). The voltage of the battery depends on cell temperature and the density of the acid solution, also its density changes with temperature and charge state. A battery with a 12V nominal voltage is constructed of 6*2V lead acid cells. The upper and lower limits of charging and discharging open circuit voltage at 25 0C are 14.4V and
10.5V respectively [13, 45].

The depth of discharge (DOD) is the state of charge of the battery. The relation between battery voltage and its depth of discharge is almost linear until a cut-off-voltage point is reached. Ope
will result in of the battery
A charge controller (regulator) is used to control operation of battery within its design

limits so that not to exceed its cut-off point, also not to exceed overcharge limit.
A lead acid battery loses so
due to internal chemical reaction. This phenomenon is called self of discharge (SOD) of the battery and it increases with increasing in battery temperature. Providing batteries with lead grid or lead-calcium grid will minimize its SOD [13, 45].
Long life-time, cycling stability rate and capability of standing very deep discharge are the main design points shall be taken into account when choose a battery for certain application.

- Lead acid battery rating and model Battery rating is commonly specified in terms of its Ampere-hour (Ah) or Watt-hour (Wh) capacity. The ampere-hour capacity of a battery is the quantity of discharge current available for a specified length of time at a certain temperature and discharge rate. High discharge current would result in reduction of the battery capacity and will decrease its life

time.
The ampere-hour efficiency of a battery (ηAh) is the ratio of amount of total Ampere- hours the battery provides during discharge to that required to charge it back to its original condition. The battery efficiency can be specified as Watt-hour efficiency (ηWh) , its definition is in the same manner as ηAh. ηWh has values lower than ηAh because the variation in voltage is taken into account [13,45] .
When the power generated from the renewable system ( wind and PV in the case under study) exceeds the load requirement, energy is stored in the battery. A minimum storage level is specified for a battery so that

should not be exceeded it. This level is a function of battery DOD so that
Where
Emin: minimum allowable capacity of the battery bank,
EBN: is the nominal capacity of battery bank, DOD : is the depth of discharge.
Energy stored in the battery at any time during charging mode can be expressed as [3]:
Energy stored in the battery at any time during discharging mode can be expressed also as [45]:
Where Eb(t) and Eb(t-1): are the charge capacity of battery bank at the time t and (t-1) respectively,
σ : is hourly self discharge rate,
EW(t) : is the energy from wind turbine during the time interval,
EPV(t) : is the energy from PV system during the time interval,
EL(t) : is the load requirement during the time interval,

ηv and ηwh : are the efficiency of inverter and

battery bank respectively.

- Battery bank sizing

The two types of lead-acid batteries available at high capacities are the regular and
the block types. The block type has long life time (>10 years), high cycling stability-rate (>
1000 times) and capability of standing very deep discharge, but has higher price than
regular batteries [13,45] .
The ampere-hour capacity (CAh ) and watt- hour capacity (CWh ) of a battery bank required to supply a load for a certain period (

day) when an energy from renewable resources is not available can be specified as follows [13,45] :
where AD : is the daily autonomy It is obvious from the above relation that total capacity of the battery depends on daily autonomy which represents number of days that battery will be capable to supply the load in case of shortage of the renewable sources.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

26

ISSN 2229-5518

To make it more clear, the sizing steps of PV
system are detailed in Appendix-C.

13-Economic evaluation [9,20,22,45]

The costs of a hybrid system include
acquisition costs, operating costs, maintenance costs and replacement costs. At end of the life of the system, the system may have a salvage value. An economic analysis is done based on life cycle costing method, which accounts for all costs associated with the system over its life time, taking into account the value of money. Life cycle costing is used in the design of the
 1  i n

PWF   

 1  d 
Where i, d and n as defined before.
Sometimes it is necessary to determine the present worth of a recurring expense, such as maintenance cost or fuel cost. In this case PWV=PWFC * Ca
Where Ca is the annual payment (cost) and PWFC is the cumulative present worth factor, and is given by:
 1  X n 

PWFC   

hybrid system that will cost the least amount
over its lifetime. Cost annuity (cost required to generate 1 kWh of energy) is an indication on
where

 1  X 

X   1  i 

the cost of the system so that the system with  
the least cost annuity is selected.

13.1 Life Cycle Cost

- Time value of money

The life cycle cost of an item consists of the
total cost of procurement and operating this item over its lifetime. Some costs involved in the procurement and operating of an item are incurred at the time of an acquisition (includes costs of purchasing equipments and installation them), and other costs are incurred at later times (includes costs of fuel if exists, operation and maintenance). The later costs may occur at regular basis or/and at irregular basis. In order to compare two similar items, which may have different costs at different times; it is convenient to refer all costs to the time of acquisition.
Two phenomena affect the value of money over time and shall be considered when evaluating economically the hybrid systems:
- The inflation rate (i) is a measure of decline in value of money. The inflation rate of any item need not necessarily follow the general inflation rate.
- The discount rate (d) relates to the amount of interest that can be earned on the principal that
is saved in a certain account.

- Present worth analysis [9]

A future amount of money for an item
converted into its equivalent present value is called the present worth (PW) of this item. For an item to be purchased (n) years later with a value of (C0) , the present worth value (PWV) is given by

PWV = PWF * C0

Where PWF is the present worth factor, and is
given by
 1  d 

13.2 Costs of PV modules

Any PV module is characterized by its peak watt (Wp )at standard test conditions. Price of
PV module depends mainly on its rated power (peak power) and its type. Table (9) shows different types of PV modules according to their rated power and manufacturer, price of each module, and the cost in ($/Wp ) for each
module. It is obvious that as rated power of a
module increases, the cost ($/Wp ) decreases. For high rated power it can be considered about 5 ($/Wp ) [www.affordable-solar.com] .
The values of installation costs vary for different applications and projects and depend mainly on the location of installation and mounting structures. For domestic applications, it can be considered about 16% of capital costs.

Table (9): the cost in $/Wp for different types of

PV modules[45].

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

27

ISSN 2229-5518

PV maintenance costs are often collected in monthly payments that cover system inspection by a maintenance person. The PV panels are in many cases assumed to have life times of more than 20 years. During its lifetime no PV panel replacement costs occur.

13.3 Costs of batteries

Any battery is characterized by its nominal
voltage and its rated Ah capacity. The 2V cell block batteries are the most common ones in the hybrid systems. Their prices are higher than the prices of regular batteries, but as mentioned before they are characterized by their high cycling rate and capability to stand very deep discharge. Table (10) shows different types of batteries according to their capacity and manufacturer, price of each one, and cost in ($/kWh) for each. As it is obvious, these cost values vary in the range 250-290 ($/kWh) [www.affordable-solar.com].
Battery operation costs comprise expenses for maintenance and replacement. Maintenance includes checking the battery electrolyte levels. Battery maintenance costs are often included in the maintenance costs of the over all system. Battery lifetime is rated on the charge- discharge cycles that it attains at the specified DOD. Number of cycles decreases as DOD percentage assumed during system operation increases. During real system operations, batteries are to a large extent partially cycled and this affects the actual battery life time [45].

Table (10): the cost in $/Wp for different types of batteries [45].

14-Modeling and simulation

14.1 Modeling a PV Cell [5,13,27-30,42,43]

The use of equivalent electric circuits

I-The Simplest Model

The simplest model of a PV cell is shown as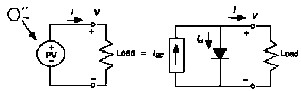

an equivalent circuit below that consists of an ideal current source in parallel with an ideal diode. The current source represents the current generated by photons (often denoted as Iph or IL), and its output is constant under constant temperature and constant incident radiation of light, fig.(47).

Figure (47): PV cell with a load and its simple equivalent circuit [27-30,42,43].

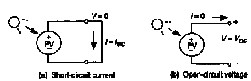
There are two key parameters frequently used to characterize a PV cell. Shorting together the terminals of the cell, as shown in Figure (48-a), the photon generated current will follow out of the cell as a short-circuit current (Isc). Thus, Iph = Isc. As shown in Figure (48-b), when there is no connection to the PV cell (open-circuit), the photon generated current is shunted internally by the intrinsic p-n junction diode. This gives the open circuit voltage (Voc). The PV module or cell manufacturers usually provide the values of these parameters in their datasheets.

Figure (48): Diagrams showing a short- circuit and an open-circuit condition [27-

30,42,43]

The output current (I) from the PV cell is found by applying the Kirchoff’s current law (KCL) on the equivalent circuit shown in Figure (47).

I=Isc- Id ----------------(1)

Where: Isc is the short-circuit current that is
equal to the photon generated current, and Id
is the current shunted through the intrinsic
diode.
The diode current Id is given by the
Shockley’s diode equation:

 q*Vd 

 

makes it possible to model characteristics

I  I

* (e K *T  1)

---------------(2)

 

of a PV cell. The method used here is d o

implemented in MATLAB programs for

Where: Io is the reverse saturation current of

simulations. The same modeling technique is also applicable for modeling a PV

diode (A),

q is the electron charge (1.602×10

-19

C),

module.

Vd is the voltage across the diode (V),

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

28

ISSN 2229-5518

k is the Boltzmann’s constant (1.381×10-23

J/K),

T is the junction temperature in Kelvin (K).

Replacing Id of the equation (1) by the equation (2) gives the current-voltage relationship of the PV cell.

 q*Vd 

 

I  I sc

 Io

* (e K *T   1)

----------------(3)

Where: V is the voltage across the PV cell, and

I is the output current from the cell.

The reverse saturation current of diode (Io) is constant under the constant temperature and found by setting the open-circuit condition as shown in Figure (48-b). Using the equation (3), let I = 0 (no output current) and solve for Io.

 q*Voc 

Figure (49): I-V plot of ideal PV cell under two different levels of irradiance (25 oC).[

27-30,42,43]

II- The More Accurate Model

  There are a few things that have not

0  I sc
 Io

* (e K *T   1)

 q*Voc 

------------(4)

been taken into account in the simple model and that will affect the performance

 

I sc

 Io

* (e K *T   1)

 q*Voc 

-------------(5)

of a PV cell in practice.

 

Io  I sc

/(e K *T   1)

----------------(6)

a-Series Resistance

In a practical PV cell, there is a series of resistance in a current path through the

To a very good approximation, the photon
generated current, which is equal to Isc, is directly proportional to the irradiance, the intensity of illumination, to PV cell [27-
30,42,43]. Thus, if the value, Isc, is known from the datasheet, under the standard test condition, Go=1000W/m2 at the air mass (AM)

= 1.5, then the photon generated current at any other irradiance, G (W/m2), is given by:

 q*Voc 

semiconductor material, the metal grid,

contacts, and current collecting bus [27-

30,42,43]. These resistive losses are lumped together as a series resister (Rs). Its effect becomes very conspicuous in a PV module that consists of many series- connected cells, and the value of resistance is multiplied by the number of

cells.

 

Io  I sc

/(e K *T   1)

----------------(7)

b) Parallel Resistance

This is also called shunt resistance. It is a
Figure (49) shows that current and voltage relationship (often called as an I-V curve) of an ideal PV cell simulated by MATLAB using the simplest equivalent circuit model. The discussion of MATLAB simulations will appear in Section (49). The PV cell output is both limited by the cell current and the cell voltage, and it can only produce a power with any combinations of current and voltage on the I-V curve. It also shows that the cell current is proportional to the irradiance.
loss associated with a small leakage of current through a resistive path in parallel with the intrinsic device [13]. This can be represented by a parallel resister (Rp). Its effect is much less conspicuous in a PV module compared to the series resistance, and it will only become noticeable when a number of PV modules are connected in parallel for a larger system.

c) Recombination

Recombination in the depletion region of PV cells provides non-ohmic current paths in parallel with the intrinsic PV cell [27-
30,42,43]. As shown in Figure (50), this can be represented by the second diode (D2) in the equivalent circuit.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

29

ISSN 2229-5518

Figure (50): More accurate equivalent circuit of PV cell

Summarizing these effects, the current- voltage relationship of PV cell is written as:

(8)

------------------

Figure (51): PV cells are connected in series to make up a PV module

Also, multiple modules can be wired together in series or parallel to deliver the voltage and current level needed. The

It is possible to combine the first diode (D1) and the second diode (D2) and rewrite the equation (2.8) in the following form.

--- (9)

where: n is known as the “ideality factor” (“n” is sometimes denoted as “A”) and takes the value between one and two [27-30,42,43].

14.2- Photovoltaic Module

A single PV cell produces an output voltage less than 1V, about 0.6V for crystalline silicon
(Si) cells, thus a number of PV cells are connected in series to archive a desired output voltage. When series-connected cells are placed in a frame, it is called as a module.
Most of commercially available PV modules with crystalline-Si cells have either 36 or 72
series-connected cells. A 36-cell module provides a voltage suitable for charging a 12V battery, and similarly a 72-cell module is appropriate for a 24V battery. This is because most of PV systems used to have backup
batteries, however today many PV systems do
not use batteries; for example, grid-tied systems.
Furthermore, the advent of high efficiency DC-DC converters has alleviated the need for modules with specific voltages. When the PV cells are wired together in series, the current output is the same as the single cell, but the voltage output is the sum of each cell voltage, as shown in Figure (51).

group of modules is called an array.

14.2.a-Modeling a PV Module

-Electrical characteristics data of PV

module taken from the datasheet

As example, BP Solar BP SX 150S PV

module, pictured in Figure (52), is chosen for a MATLAB simulation model. The module is made of 72 multi-crystalline silicon solar cells in series and provides

150W of nominal maximum power [13, 27-

30, 42,43]. Table (11) shows its electrical specification.

Figure (52): Picture of BP SX 150S PV module

[13]

Table (11): electrical specification of PV

The strategy of modeling a PV module is no different from modeling a PV cell. It uses the same PV cell model. The

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

30

ISSN 2229-5518

parameters are the all same, but only a voltage parameter (such as the open- circuit voltage) is different and must be divided by the number of cells.

The study done by Walker [13] of University
of Queensland, Australia, uses the electric model with moderate complexity, shown in Figure (53), and provides fairly accurate results. The model consists of a current source (Isc), a diode (D), and a series resistance (Rs).
The effect of parallel resistance (Rp) is very small in a single module, thus the model does not include it. To make a better model, it also includes temperature effects on the short- circuit current (Isc) and the reverse saturation current of diode (Io). It uses a single diode with the diode ideality factor (n) set to achieve the best I-V curve match.
a is the temperature coefficient of Isc in percent change per degree temperature als given in the datasheet.
The short-circuit current (Isc) is proportional to the intensity of irradiance, thus Isc at a
given irradiance (G) is:

 G 

I sc @ G  I sc @ Go  G 

 o 

--------------(12)

Where: Go is the nominal value of irradiance, which is normally 1KW/m2.
The reverse saturation current of diode (Io) at the reference temperature (Tref) is given
by the equation (2.6) with the diode ideality factor added: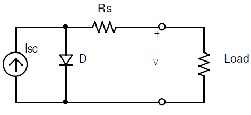

Io 

I sc

-------------(13)

(eqVoc / nKT  1)

The reverse saturation current (Io) is temperature dependant and the Io at a given
temperature (T) is calculated by the following equation [27].

Figure (53): Equivalent circuit used in the

3 qEg  1



1 

MATLAB simulations

Io @ T  Io

@ Tref

 T  n

 

T



* e nK  T



ref 

Since it does not include the effect of parallel resistance (Rp), letting Rp =  in the equation (2.9) gives the equation [13] that describes the current-voltage relationship of the PV cell, and it is shown below.

 q s  

 ref 

--------------------------------------------(14)

The diode ideality factor (n) is unknown and
must be estimated. It takes a value between one and two; the value of n=1 (for the ideal
diode) is, however, used until the more

 V  I *R 

I  I sc

(10)

 I e 





n KT

  1





----------------

accurate value is estimated later by curve
fitting [13]. Figure (54) shows the effect of the varying ideality factor.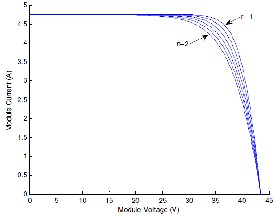

Where: I is the cell current (the same as the module current),

V is the cell voltage = {module voltage} ÷

{number of cells in series},

T is the cell temperature in Kelvin (K).

First, calculate the short-circuit current (Isc)
at a given cell temperature (T):

I sc @T  I sc @Tref 1  a(T  Tref )

-------------- (11)
where: Isc at Tref is given in the datasheet
(measured under irradiance of 1000W/m2),

Tref is the reference temperature of PV cell in

Kelvin (K), usually 298K (25 oC),

Figure (54): Effect of diode ideally factors by MATLAB simulation (1KW/m2, 25 oC)

The series resistance (Rs) of the PV module has a large impact on the slope of the I-V curve near the open-circuit voltage (Voc), as shown in Figure (55), hence the value of Rs is

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

31

ISSN 2229-5518

calculated by evaluating the slope dI of the I-

dV

V curve at the Voc [27]. The equation for Rs is

derived by differentiating the equation (2.10)
and then rearranging it in terms of Rs.
Finally, it is possible to solve the equation of
I-V characteristics (2.10). It is, however, complex because the solution of current is recursive by inclusion of a series resistance in the model. Although it may be possible to find the answer by simple iterations, the Newton’s method is chosen for rapid convergence of the answer [13]. The Newton’s method is described as:

xn 1

 xn

 f ( xn)

f ' ( xn )

-------------- (19)

16)

Where: f '(x) is the derivative of the function, f (x) =0 , xn is a present value, and x n+1 is a next value.
Rewriting the equation (2.10) gives the
following function:

---------- (17)

 q V  IR s  

Then, evaluate the equation (17) at the open circuit voltage that is V=Voc (also let I=0).

f (I )  I sc

 I  I



e 

o 



n KT



  1  0




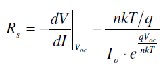
(20)

--------

where:

------ (18)

dI is the slope of the I-V curve

Plugging this into the equation (2.19) gives a following recursive equation, and the output current (I) is computed iteratively.

 V  I R 

q 

dV Voc

I sc

 I n
 I o
e 

n KT

  1

at the Voc (use the I-V curve in the datasheet
then divide it by the number of cells in series),

I n 1

 I n 
 

 

 V  I n Rs 

Voc is the open-circuit voltage of cell (found

 qR

 q  
by dividing Voc in the datasheet by the number of cells in series).
 I  I o 


s

nKT

e 


n KT

  1




The calculation using the slope measurement of the I-V curve published on the BP SX150 datasheet gives a value of the series resistance per cell, Rs = 5.1m Ω.

Figure (55): Effect of series resistances by

MATLAB simulation (1KW/m2, 25 oC)[13].

----- (21)
It was mentioned that using The MATLAB, it can performs the calculation five times iteratively to ensure convergence of the results. Also, the testing result has shown that the value of In usually converges within three iterations and never more than four interactions[ 13].

Figure (56) shows the plots of I-V characteristics at various module temperatures simulated with the MATLAB model for BP SX 150S PV module. Data points superimposed on the plots are taken from the I-V curves published on the manufacturer’s datasheet [31]. After some trials with various diode ideality factors, the MATLAB model chooses the value of n

= 1.62 that attains the best match with the I-V curve on the datasheet. The figure shows good correspondence between the data points and the simulated I-V curves.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

32

ISSN 2229-5518

Figure (56): I-V curves of BP SX 150S PV module at various temperature Simulated with the MATLAB model (1KW/m2, 25 oC)[13].

14.3 The I-V Curve and Maximum

Power Point

Figure (57) shows the I-V curve of the

BP SX 150S PV module simulated with the MATLAB model. A PV module can produce the power at a point, called an operating point, anywhere on the I-V curve. The coordinates of the operating point are the operating voltage and current. There is a unique point near the knee of the I-V curve, called a maximum power point (MPP), at which the module operates with the maximum efficiency and produces the maximum output power. It is possible to visualize the location of the by fitting the largest possible rectangle inside of the I-V curve, and its area equal to the output power which is a product of voltage and current.

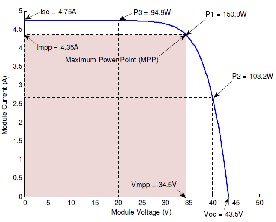
Figure (57): Simulated I-V curve of BP SX 150S PV module (1KW/m2, 25 oC)[13].

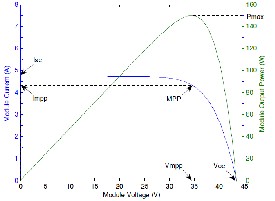
The power vs. voltage plot is overlaid on the I-V plot of the PV module, as shown in Figure (58). It reveals that the amount of power produced by the PV module varies greatly depending on its operating condition. It is important to operate the system at the MPP of PV module in order to exploit the maximum power from the module. The next chapter will discuss how to do it.

Figure (58): I-V and P-V relationships of BP SX

150S PV module Simulated with the MATLAB

model (1KW/m2, 25 oC)[13]

15-Maximum Power Point Tracker

15.1- Effect of load type

When a PV module is directly coupled to a
load, the PV module’s operating point will be at the intersection of its I–V curve and the load line which is the I-V relationship of load. For example in Figure (59-a), a resistive load has a straight line with a slope of 1/Rload as shown in Figure (60). In other words, the impedance of load dictates the operating condition of the PV module. In general, this operating point is seldom at the PV module’s MPP, thus it is not producing the maximum power. A study shows that a direct-coupled system utilizes a mere
31% of the PV capacity [13]. A PV array is usually oversized to compensate for a low power yield during winter months. This mismatching between a PV module and a load requires further over-sizing of the PV array and thus increases the overall system cost. To mitigate this problem, a maximum power point tracker (MPPT) can be used to maintain the PV module’s operating point at the MPP. MPPTs can extract more than 97% of the PV power when properly optimized [9].

This section discusses the I-V characteristics of PV modules and loads, matching between the two. It also discusses the details of some MPPT algorithms and control methods, and limitations of MPPT.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

33

ISSN 2229-5518

Figure (59-a): PV module is directly connected to a (variable) resistive load

Figure (59-b): Electrical model of permanent magnet DC motor

Figure (59): PV module is directly

connected to Different loads[13]

Figure (60): I-V curves of BP SX 150S PV module and various resistive loads Simulated with the MATLAB model (1KW/m2, 25 oC)[13].

2- DC Motors load

As example, Many PV water pumping systems employ DC motors (instead of AC motors) because they could be directly coupled with PV arrays and make a very simple system. Among different types of DC motors, a permanent magnet DC (PMDC) motor is preferred in PV systems because it can provide higher starting torque. Figure (59-b) shows an electrical model of a PMDC motor. When the motor is turning, it produces a back emf, or a counter electromotive force, described as an electric potential (E) proportional to the angular speed (ω) of the rotor. From the equivalent circuit, the DC voltage equation for the armature circuit

is:

where: Ra is the armature resistance.
The back emf is E=K·ω where: K is the constant, and ω is the angular speed of rotor in rad/sec.
Figure (61) shows an example of current- voltage relationship (I-V curve) of a DC motor. Applying the voltage to start the motor, the current rises rapidly with increasing voltage until the current is sufficient to create enough starting torque to break the motor loose from static friction [13]. At start-up (ω=0), there is no effect of back emf, therefore the starting current builds up linearly with a steep slope of

1/Ra on the I-V plot as shown in Figure (61). Once it starts to run, the back emf takes effect and drops the current, therefore the current rises slowly with increasing voltage.

As usual already a simple type of PV water pumping systems uses a direct coupled PV-
motor setup. This configuration has a severe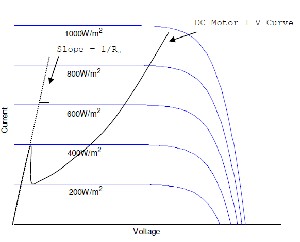

disadvantage in efficiency because of a mismatched operating point, as shown in Figure (61). For this example, the water pumping system would not start operating until irradiance reaches at 400W/m2. Once it starts to run, it requires as little as 200W/m2 of irradiance to maintain the minimum operation. This means that the system cannot utilize a fair amount of morning insolation just because there is insufficient starting torque. Also, when the motor is operated under the locked condition for a long time, it may result in shortening of the life of the motor due to input electrical energy converted to heat rather than to mechanical output [13].

Figure (61): PV I-V curves with varying irradiance and a DC motor I-V curve[13].

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

34

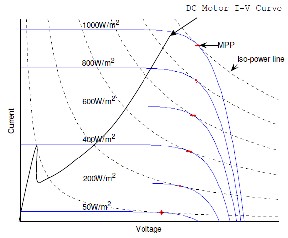
ISSN 2229-5518

Figure (63): PV I-V curves with iso-power lines (dotted) and a DC motor I-V curve[13]

There is a MPPT specifically called a linear current booster (LCB) that is designed to overcome the above mentioned problem in water pumping systems. The MPPT maintains the input voltage and current of LCB at the MPP of PV module. As shown in Figure (63), the power produced at the MPP is relatively low-current and high-voltage which is opposite of those required by the pump motor. The LCB shifts this relationship around and converts into high-current and low-voltage power which satisfies the pump motor characteristics. For the example in Figure (63), tracing of the iso- power (constant power) line from the MPP reveals that the LCB could start the pump
motor with as little as 50W/m2 of irradiance (assuming the LCB can convert the power without loss).

15.2 Maximum Power Point

Tracking Algorithms[5,13,24]

The location of the MPP in the I–V plane is
not known beforehand and always changes dynamically depending on irradiance and temperature. For example, Figure (64) shows a set of PV I–V curves under increasing irradiance at the constant temperature (25 oC), and Figure (65) shows the I–V curves at the same irradiance values but with a higher temperature (50 oC). There are observable voltage shifts where the MPP occurs. Therefore, the MPP needs to be located by tracking algorithm, which is the heart of MPPT controller.
There are a number of methods that have been proposed. One method measures an open- circuit voltage (Voc) of PV module every 30 seconds by disconnecting it from rest of the circuit for a short moment. Then, after re- connection, the module voltage is adjusted to
76% of measured Voc which corresponds to
the voltage at the MPP [13] (note: the

percentage depends on the type of cell used). The implementation of this open-loop control method is very simple and low-cost although the MPPT efficiencies are relatively low (between 73~91%) [13]. Model calculations can also predict the location of MPP; however in practice it does not work well because it does not take physical variations and aging of module and other effects such as shading into account. Furthermore, a pyranometer that measures irradiance is quite expensive. Search algorithm using a closed-loop control can achieve higher efficiencies, thus it is the customary choice for MPPT. Among different algorithms, the Perturb & Observe (P&O) and Incremental Conductance (incCond) methods are studied here.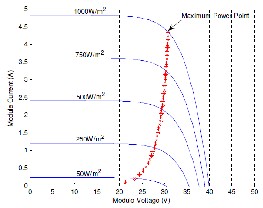

Figure (64): I-V curves for varying irradiance and a trace of MPPs (25 oC)

Figure (65): I-V curves for varying irradiance and a trace of MPPs (50 oC) [13]

I- Perturb & Observe Algorithm

The perturb & observe (P&O) algorithm,
also known as the “hill climbing” method, is very popular and the most commonly used in practice because of its simplicity in algorithm and the ease of implementation. The most basic form of the P&O algorithm operates as follows. Figure (66) shows a PV module’s output power curve as a function of voltage (P- V curve), at the constant irradiance and the

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

35

ISSN 2229-5518

constant module temperature, assuming the PV module is operating at a point which is away from the MPP.
In this algorithm the operating voltage of the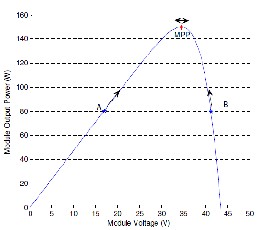

PV module is perturbed by a small increment, and the resulting change of power, ΔP, is observed. If the ΔP is positive, then it is supposed that it has moved the operating point closer to the MPP. Thus, further voltage perturbations in the same direction should move the operating point toward the MPP. If the ΔP is negative, the operating point has moved away from the MPP, and the direction of perturbation should be reversed to move back toward the MPP. Figure (67) shows the flowchart of this algorithm.

Figure (66): Plot of power vs. voltage for

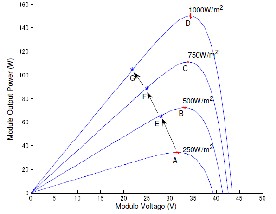
BP SX 150S PV module (1KW/m2, 25oC)

Figure (68): Erratic behavior of the P&O algorithm under rapidly increasing irradiance

Figure (67): Flowchart of the P&O

algorithm[13].

There are some limitations that reduce its MPPT efficiency. First, it cannot determine when it has actually reached the MPP. Instead, it oscillates the operating point around the MPP after each cycle and slightly reduces PV efficiency under the constant irradiance condition [13]. Second, it has been shown that it can exhibit erratic behavior in cases of rapidly changing atmospheric conditions as a result of moving clouds [13]. The cause of this problem can be explained using Figure (68) with a set of P-V curves with varying irradiance.
Assume that the operating point is initially at the point A and is oscillating around the MPP at the irradiance of 250W/m2. Then, the irradiance increases rapidly to 500W/m2. The power measurement results in a positive ΔP. If this operating point is perturbing from right to left around the MPP, then the operating point will actually moves from the point A toward the point E (instead of B). This happens because the MPPT can not tell that the positive ΔP is
the result of increasing irradiation and simply assumes that it is the result of moving the operating point to closer to the MPP. In this case the positive ΔP is measured when the operating voltage has been moving toward the left; the MPPT is fooled as if there is a MPP on the left side. If the irradiance is still rapidly increasing, again the MPPT will see the positive ΔP and will assume it is moving towards the MPP, continuing to perturb to the left.
From points A, E, F and G, the operating point continues to deviate from the actual MPP until the solar radiation change slows or settles down. This situation can occur on partly cloudy days, and MPP tracking is most

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

36

ISSN 2229-5518

difficult because of the frequent movement of the MPP.
The advent of digital controller made implementation of algorithm easy; as a result many variations of the P&O algorithm were proposed to claim improvements. The problem
of oscillations around the MPP can be solved by the simplest way of making a bypass loop which skips the perturbation when the ΔP is very small which occurs near the MPP. The tradeoffs are a steady state error and a high risk of not detecting a small power change.

Another way is the addition of a “waiting” function that causes a momentary cessation of perturbations if the direction of the perturbation is reversed several times in a row, indicating that the MPP has been reached [13]. It works well under the constant irradiation but makes the MPPT slower to respond to changing atmospheric conditions. A more complex one uses a variable step size of perturbation, using the slope of PV power as a variable, for example:
Again, this works well under the constant irradiation but worsens the erratic behavior under rapidly changing atmospheric conditions on partly cloudy days because the power change due to irradiance makes the step size too big. A modification involving taking a PV power measurement twice at the same voltage solves the problem of not detecting the changing irradiance [13]. Comparing these two measurements, the algorithm can determine whether the irradiance is changing and decide how to perturb the operating point. The tradeoff is that the increased number of sampling slows response times and increases the complexity of algorithm.

II- Incremental Conductance

Algorithm

In 1993 Hussein, Muta, Hoshino, and
Osakada of Saga University, Japan, proposed the incremental conductance (incCond) algorithm intending to solve the problem of the P&O algorithm under rapidly changing
atmospheric conditions [13].
The basic idea is that the slope of P-V curve becomes zero at the MPP, as shown in Figure
3-13. It is also possible to find a relative location of the operating point to the MPP by looking at the slopes. The slope is the derivative of the PV module’s power with
respect to its voltage and has the following
relationships with the MPP.
------- (18-20)

The above equations are written in terms of voltage and current as follows. (21)

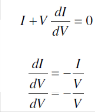
If the operating point is at the MPP, the eq mes:
--------------- (22,23)
If the operating point is at the left side of the
MPP, the equation (3.21) becomes: 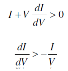--------------- (24, 25)
If the operating point is at the right side of the MPP, the equation (3.21) becomes:
---------------- (26, 27)
Note that the left side of the equations (23), (25), and (27) represents incremental conductance of the PV module, and the right side of the equations represents its instantaneous conductance.

The flowchart shown in Figure (69) explains the operation of this algorithm. It starts with measuring the present values of PV module voltage and current. Then, it calculates the incremental changes, dI and dV, using the present values and previous values of voltage and current. The main check is carried out using the relationships in the equations (23), (25), and (27). If the condition satisfies the inequality (25), it is assumed that the operating point is at the left side of the MPP thus must be moved to the right by increasing the module voltage. Similarly, if the condition satisfies the inequality (27), it is assumed that the

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

37

ISSN 2229-5518

operating point is at the right side of the MPP, thus must be moved to the left by decreasing the module voltage. When the operating point reaches at the MPP, the condition satisfies the equation (23), and the algorithm bypasses the voltage adjustment.

At the end of cycle, it updates the history by storing the voltage and current data that will be used as previous values in the next cycle. Another important check included in this algorithm is to detect atmospheric conditions. If the MPPT is still operating at the MPP (condition: dV = 0) and the irradiation has not changed (condition: dI = 0), it takes no action. If the irradiation has increased (condition: dI >

0), it raises the MPP voltage. Then, the algorithm will increase the operating voltage to track the MPP. Similarly, if the irradiation has decreased (condition: dI<

0), it lowers the MPP voltage. Then, the algorithm will decrease the operating voltage.

Figure (69): Flowchart of the incCond algorithm[13]

In practice, the condition dP/dV = 0 (or dI/dV = -I/V) seldom occurs because of the approximation made in the calculation of dI and dV [13]. Thus, a small margin of error (E) should be allowed, for example: dP/dV = ±E. The value of E is optimized with exchange between an amount of the steady-sate tracking error and a risk of oscillation of the operating point.

15.3- Control of MPPT[5,13,,24]

As explained in the previous section, the
MPPT algorithm tells a MPPT controller how
to move the operating voltage. Then, it is a MPPT controller’s task to bring the voltage to a desired level and maintain it. There are several methods often used for MPPT:
-PI Control
- Direct Control
- Output Sensing Direct Control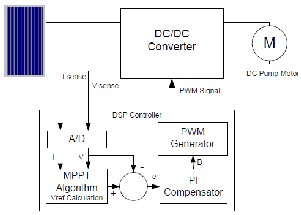

the block diagram for the first two types is given below in figures(70 and 71):

Figure (70): Block diagram of MPPT with the PI compensator[13]

Figure (71): Block diagram of MPPT with the direct control[13].

15.4- Limitations of MPPT

From the above explanation, it’s obvious
that there is no regulation of the output voltage and current. If the application requires a constant voltage, it must employ batteries to maintain the voltage constant. For water
pumping system without batteries, the lack of output regulation is not a predicament as long
as they are equipped with water reservoirs to
meet the demand of water. The speed of pump motor is proportional to the converter’s output voltage which is relative to irradiation. Thus, when the sun shines more, it simply pumps more water.
Another noteworthy fact is that MPPT stops its original task if the load cannot consume all

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

38

ISSN 2229-5518

the power delivered. For the stand-alone system, when the load is limited by its maximum voltage or current, the MPPT moves the operating point away from the MPP and sends less power. It is very important to select an appropriate size of load, thus it can utilize the full capacity of PV module and array. On the other hand, the grid-tied system can always perform the maximum power point tracking because it can inject the power into the grid as much as produced.

Of course, in reality DC-DC converter used in MPPT is not 100% efficient. The efficiency gain from MPPT is large, but the system needs to take efficiency loss by DC-DC converter into account. There is also tradeoff between efficiency and the cost. It is necessary for PV system engineers to perform economic analysis of different systems and also necessary to seek other methods of efficiency improvement such as the use of a sun tracker.

16- Solution technique for

Simulation of PV Module [27-

30,42,43]

The blocks of the model can be developed using MATLAB /Simulink based on the set of
Equations mentioned above. The Solarex MSX60/MSX64 PV modules are chosen for modeling. The typical electrical characteristics
of both MSX60 and MSX 64 are given in table
(11). These modules consist of 36 polycrystalline silicon solar cells electrically configured as two series strings of 18 cells each [13].
The blocks developed using MATLAB/simulink for the PV module is shown in Appendix-B.
The I-V characteristics and P-V characteristics curves obtained from the simulation are also presented in Appendix-B

17- Conclusion

Issues of energy and global warming are
some of the biggest challenges for humanity in the 21st century. Energy is so important for everyone, and in fact, taking control of the world’s supply of oil is one of the most important national agenda for United Sates. In contrast, renewable energy resources are ubiquitous around the world. Especially, PV has a powerful attraction because it produces electric energy from a free inexhaustible source, the sun, using no moving parts, consuming no fossil fuels, and creating no pollution or green house gases during the
power generation. Together with decreasing PV module costs and increasing efficiency, PV is getting more pervasive than ever.
The use of PV solar energies appears
nowadays as a reasonable and technically attractive option towards the emerging and stressing energy problems.
A PV module model based on the mathematical model of solar cell can be developed using MATLAB/Simulink blocks. The essential input parameters such as Vm, Im, Voc, Isc, Ns, KI, Tc and G are taken from the manufacturer's datasheet. The I-V and P-V characteristics outputs can be generated using the developed model at different operating parameters, for the selected modules. The obtained results are well matched with the design ones.
Finally, the study validates that MPPT can significantly increase the efficiency of energy production from PV compared to the system without MPPT.

Nomenclature

ACT Total Annual Cost ART Total Annual Revenue a-Si Amorphous-Silicon BOS Balance of System

CI(G)S Copper Indium(Gallium) Diselenide

COE Cost of Energy DOD Depth of Discharge EPBT Energy Pay Back Time

ISC Short Circuit Current kWh Kilo Watt Hour

LCC Life Cycle Cost

MPPT Maximum Power Point tracker

NOCT Normal Operating Cell Temperature

NPV Net Present Value PSH Peak Sun Hour PV Photovoltaic

PWF Present Worth Factor

PWFC Cumulative Present Worth Factor

PWV Present Worth Value

SC-Si Single Crystaline-Silicon

SOC State of Charge

SOD Self of Discharge

VOC Open Circuit Voltage

Wp Watt peak

REFERENCES

[1] El-Ghonemy, A.M.K. 2012" Water desalination systems powered by renewable energy sources: Review" Renewable and Sustainable Energy Reviews, 16, p. 1537–

1556.

[2]Markvart, T. and Castaner, L.,2003 "Practical Handbook of Photovoltaics, Fundamentals and Applications" Elsevier,

2003.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

39

ISSN 2229-5518

[3]Castaner, L., 2002 "Modelling Photovoltaic

Systems Using PSpice" CRC Press, 2002.

[4] Ross, R.G., 1980 "Flat-plate photovoltaic array design optimization," in 14th IEEE Photovoltaic Specialists Conference, pp. 1126-

1132, March 1980.

[5] Gwinyai D.B.S., 2008 " MODELING OF PHOTOVOLTAIC SYSTEMS" M.Sc thesis,

The Ohio State University.

[6]Global market outlook for photovoltaics until

2014, European photovoltaic industry association (EPIA)

[7]Waldau, A.J., 2012"Thin Film Photovoltaics: Markets and Industry"Hindawi Publishing

Corporation, International Journal of

Photoenergy, Article ID 768368, 6 pages.

[8]AbKadir, M.Z.A., Rafeeu, Y., Adam, N.M., 2010" Prospective scenarios for the full solar energy development in

Malaysia: Renewable and Sustainable

Energy Reviews, 14, 3023–3031.

[9] Ummel, K, Wheeler, D., 2008" " Desert Power: The Economics of Solar Thermal Electricity For Europe, North Africa, and the Middle East" Center for Global Development.

[10]Alawaji, S.H., Hasanain, S.M., 1999 "Role of Solar Energy Research in Transferring of Technology to Saudi Arabia", Energy Sources, 21:923 ] 934,

1999.

[11]Alawaji,S.H., 2001 "Evaluation of solar energy research and its application in Saudi Arabia – 20 years of experience,", Renewable & Sustainable Energy Reviews, Vol.5, 59-77.

[12]Al-Abbadi, N.M., Alawaji, S.H., Bin Mahfoodh, M.Y, Myers, D.R, and Anderberg, M., 2002"Saudi Arabian solar radiation network operation data collection and quality assessment" Renewable Energy 25 () 219–234.

[13]Akihiro Oi, 2005 "DESIGN AND SIMULATION OF PHOTOVOLTAIC WATER PUMPING SYSTEM" M.Ss thesis, California Polytechnic State University, San Luis Obispo.

[14]Carr, A.J., 2005" A detailed performance comparison of PV modules of different

technologies and the implications for the PV system design method", PhD thesis, Murdoch university, Western Australia.

[15] M. D. Archer and R. Hill, Clean Electricity

from photovoltaics. Imperial College Press,

2001.

[16] G. A., 2003"Photovoltaic materials, history, status and outlook" Materials Science and

Engineering: R: Reports, vol. 40, pp. 1{46, January 2003.

[17] Green, Y. H. , Emery, K., 2008 "Short communication solar cell efficiency tables

(version 31)," Progress in Photovoltaics: Research and Applications, vol. 16, p. 435440,

2008.

[18] R. Messenger and G. Ventre, "Photovoltaic

Systems Engineering" Second Edition, Wiley,

2003.

[19] K. Töpfer,2009 “Decarbonisation of energy supply – central challenge for mankind” Clean Power from Deserts, The DESERTEC Concept for Energy, Water and Climate Security, WhiteBook · 4th Edition.

[20] Leva, S., Zaninelli, D., 2006 "Technical and Financial Analysis for Hybrid Photovoltaic Power Generation Systems" WSEAS

Transactions on Power Systems, Vol. 5, no.1, pp.831-838

[21] S. Leva, D. Zaninelli, R. Contino" Integrated renewable sources for supplying

remote power systems" WSEAS Transactions on Power Systems, vol.2, no.2, February 2007, pp.41-48

[22] Schaefer, J., 1990 "Review of Photovoltaic

Power Plant Performance and Economics" IEEE Trans. Energy Convers., Vol. EC-5,pp.

232-238.

[23] Markvart T.: “Solar Electricity”, John Wiley

& Sons, 1994.

[24] C. C. Hua and C. M. Shen, “Study of maximum power tracking techniques and control of dc-dc converters for photovoltaic

power system,” Proceedings of 29th annual IEEE Power Electronics Specialists Conference, vol. 1, 1998, pp. 86-93.

[25] H. S. Rauschenbach" Solar cell array design

handbook" Van Nostrand Reinhold, 1980.

[26] Angrist, S. W. 1982"Direct Energy Conversion" Allyn and Bacon, Inc., 4th edition, pp. 177-227.

[27] O. Wasynczuk, “Dynamic behavior of a class

of photovoltaic power systems,” IEEE Transactions on Power Apparatus and Systems, Vol. PAS-102, no. 9, 1983, pp. 3031-3037.

[28] J. C. H. Phang, D. S. H. Chan, and J. R.

Philips, “Accurate analytical method for the extraction of solar cell model parameters,” Electronics Letters, vol. 20, no. 10, 1984, pp.406-408.

[29] W. De Soto, S. A. Klein, and W. A. Beckman. "Improvement and validation of a model for photovoltaic array performance" Solar Energy, 80(1):78–88, January 2006.

[30] Marcelo Gradella Villalva, Jonas Rafael Gazoli, Ernesto Ruppert Filho“Modeling and Circuit-based Simulation of photovoltaic arrays” 10th Brazilian Power Electronics

Conference (COBEP), 2009.

[31]Solarex MSX60/64 datasheet. Available online at: http://www.californiasolarcenter.org

/newssh/pdfs/Solarex- MSX64.pdf

[32]Eltawil M.A, Zhengming Z., and Yuan.L., 2009,"Areview of renewable energy technologies integrated with desalination systems", Renewable and Sustainable Energy Review, Vol 13 PP

2245–2262..

[33]Kalogirou, S.A, 2005,"Seawater desalination using renewable energy sources" Progress in Energy and Combustion Science, vol. 31, pp 242–281.

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

40

ISSN 2229-5518

[34]Trieb,F., Scharfe, J., Kern,J.

Nieseor,T., Glueckstern, P.,

2009"Combined Solar Power and Desalination Plants: Techno-Economic Potential in Mediterranean Partner Countries", (MED-CSP), Work Package

1 Leader Organization: DLR.

[35]Al-Karaghouli, A., and Kazmerski, L.L.,

2011 " Renewable Energy Opportunities in Water Desalination" National Renewable Energy Laboratory (NREL),Golden, Colorado, 80401, USA.

[36] Al-Karaghouli, A. and Kazmerski, L.L.,

2010" Economic Analysis of a Brackish Water Photovoltaic-Operated (BWRO- PV) Desalination System" National Renewable Energy Laboratory Golden, Colorado 80401 (USA).

[37]El-Nashar,AM.,1992 "Optimising the operating parameters of a solar desalination plant." Solar Energy,

48(4):207–13.

[38]Alawaji, S, Smiai, M.S, Rafique, S., 1995" PV-powered water pumping and desalination plant for remote areas in Saudi Arabia" Applied energy, 52,283-289.

[39]Hasnain, S.M, Alajlan, S, 1998"

Coupling of PV-Powered RO brachish water desalination plant with solar stills" Reneable energy, vol.14, nos.1-4,pp281-

286

[40] Ghermandi, A., Messalem, R., 2009" Solar-driven desalination with reverse osmosis: the state of the art" Desalination and Water Treatment, vol.7 , PP 285–296. [41]Desalination Units powered by Renewable Energy Systems, Opportunities and Challenges, 2005" Organized by INRGREF, Proceedings of

the International Seminar held in

Hammamet, Tunisia,.

[42] Huan-Liang Tsai, 2010" Insolation- oriented model of photovoltaic module using Matlab/Simulink" Solar Energy, Vol. 84, No.

7, pp. 1318-1326.

[43]Kashif Ishaque, Zainal Salam, and

Syafaruddin, 2011" A

comprehensive MATLAB-Simulink PV system

simulator with partial shading capability based on two-diode model"

[44] ULUOĞLU,A., 2010"SOLAR-HYDROGEN

STAND-ALONE POWER SYSTEM DESIGN AND SIMULATIONS"MSc thesis, THE GRADUATE SCHOOL OF NATURAL AND APPLIED SCIENCES OF MIDDLE EAST TECHNICAL UNIVERSITY.

[45] Abdel-Qader,M.S.I.,2008"Simulation of a Hybrid Power System Consisting of Wind Turbine, PV, Storage Battery and Diesel

Generator with Compensation Network: Design, Optimization and Economical Evaluation" MSc thesis , Faculty of Graduate Studies, at An-Najah National University,

Nablus, Palestine

Appendix-A

-Applications of Solar energy in KSA [10,11]:

A brief description of the major projects
executed in Saudi Arabia is given in Appendix (A2)[14-28]. After two decades from operation, the performance results and lessons learned through operation and maintenance of selected projects we discussed and reported by Alawaji, S.H [14]. All projects are divided into the following categories,
1-PV power plant (The Solar Village Project).
2- Solar-Powered Water Desalination Projects
3-The Solar Thermal Dish Project coupled with Stirling engines to convert the collected solar thermal energy into mechanical energy.
4-The 350 kW Solar Hydrogen Production Project (solar-powered hydrogen- generation plant)
5-The Solar-Powered Hydrogen Utilization Project (using an internal combustion engine enabled it to use hydrogen as a fuel instead of petrol or gasoline.
6- The Solar-Powered Highway Devices
Project (lightning)
7- Solar dryers (drying dates by solar energy)
8- The Solar Water Heating Project
9- The Solar Energy Education and Training
Project.

Appendix-B

The MATLAB / Simulink PV model (at insolation of 600, 1000 w/m2)

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

41

ISSN 2229-5518

Appendix-C: sizing steps of PV system:

I-Input data for system parameters:

1-concurrent load factor: how much of the total possible load can be expected at any point of time?
0 =100%
2-Inverter efficiency , ηinv. Typuical 0.85:0.9
3-System voltage 12 or 24 or 48V in residential electric load voltage sstems.
4- Das of autonomy: how many days should the system continue to provide energy without input
(due to bad weather).
5-Daily depth of discharge: The acceptable depth of battery discharge each day(typically 10:50%, where discharging battery below 50% is not recommended).
6 –battery efficiency, ηbatt : 0.8:0.9

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

42

ISSN 2229-5518

7-The number of Peak sun hours per day(PSH): it depends on geographic location of place.
8-PV module wattage: could be from 50- 200 Watt.
9- system voltage and current : assume total AC load =

II-Calculations of appliances loads:

1-For AC loads:

- total nominal AC load =A=740 W
-total nominal AC energy=B=1840 Wh (according to working hrs for each appliance)
-Total AC surge power=C=4180 W Note:
- Total AC load considering surge factor=sum(individual appliance nominal load * its surge factor) in Watt
-Total AC load in Watt hours= sum(individual appliance nominal load * working hrs per day) in
Wh

2- For DC loads

-Total nominal DC load= D =265 W
-Total nominal energy= E=140
-total surge DC power=F=D=265W (surge factor=1 for DC appliances)
II- system voltage and current
- Total AC Load / Inverter Efficiency Factor=G=A/( ηinv=0.85)= 870.5882353
-total DC load =D=262W
-total load= G+D= H=1135.588235 W
-total load* Concurrent Load Factor =I= H * Concurrent Load Factor(0.5)= 567.7941176 W.
-desired system voltage=J=24V
- System Amperage @ System Voltage=k=I/J= 23.65808824A

III-System components: Inverter:

-Continuous Power=A=740W
- Surge Power=C= 4180W
- Continuous Power x Concurrent Load Factor=L=A* Concurrent Load Factor(0.5)= 370W
- Surge Power x Concurrent Load Factor=m=C* Concurrent Load Factor(0.5)=2090W

Batteries:

- Total Energy Use=N=B+E=1890Wh
- Inverter Input Energy=O=B* ( ηinv=0.85)= 2164.705882Wh.
- DC Energy Use=E=140Wh
- Battery Output Energy=P=O+E=2304.705882Wh.
- Battery Output Energy x Days Of Autonomy=Q=P*(Days of autonomy=5)= 11523.52941Wh.
- Battery Total (Wh)=R=P/(100/DOD%)=23047.05882Wh.
- Battery Total (Ah)= R/(system voltage(24V)= 960.2941176Ah.

PV modules:

- Daily Energy Input Into Battery==T=P/( ηbatt=0.8)= 2880.882353Wh.
- Hourly Energy Input Into Battery=U=T/(peak sun hours=5)= 576.1764706Wh.
- Number Of Modules=V=U/(PV module wattage=80W)= 7.202205882
- Number Of Modules (Rounded Up)=Round(V)=8.

Regulator

-System voltage=J=24V
-System Amperage=K= 23.65808824

IJSER © 2012 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 3, Issue 11, November-2012

43

ISSN 2229-5518

Maximum Depth Of Discharge 50%

2: APPLIANCES

2.1: AC Loads Number Power (W) Hours (H) Energy (Wh) Surge Factor Surge (W)

Fridge 1 160 8 1280 6 960

Washing Machine 1 500 0.5 250 6 3000

TV 1 70 4 280 3 210

Powerpack 1 10 3 30 1 10

Total AC Load 740 1840 4180

2.2: DC Loads Number Power (W) Hours (H) Energy (Wh) Surge Factor Surge (W)

Compact Fluoro 1 15 1 15 1 15

Pump 1 250 0.5 125 1 250

Total DC Load 265 140 265

3: SYSTEM VOLTAGE AND CURRENT

4: SYSTEM COMPONENTS

4.1 Inverter

4.2: Batteries

Continuous Power 740 W Surge Power 4180 W Continuous Power x Concurrent Load Factor 370 W Surge Power x Concurrent Load Factor 2090 W

Calculations Total Energy Use 1980 Wh Inverter Input Energy 2164.7 Wh DC Energy Use 140 Wh Battery Output Energy 2304.7 Wh Battery Output Energy x Days Of Autonomy 11524 Wh Battery Total (Wh) 23047 Wh

Battery Total (Ah) 960.29 Ah

4.3: PV Modules

4.4: Regulator

Daily Energy Input Into Battery 2880.9 Wh Hourly Energy Input Into Battery 576.18 Wh Number Of Modules 7.2022

Number Of Modules (Rounded Up) 8

System Voltage 24 V System Amperage 23.658 A

IJSER © 2012 http://www.ijser.org