International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 1
ISSN 2229-5518
Phase Shifts of Electron-Atom Scattering Using
J-Matrix Method for a Class of Short Range
Potentials
Nawzat S. Saadi1, Badal H. Elias 2
Abstract— This study deals with the non-relativistic J-matrix method in quantum scattering theory. The method is investigated for a class of short range scattering potentials (Yukawa, Hulthén, and Exponential-Cosine Screened Coulomb), and in two different L2 basis (Laguerre and Gaussian) for elastic electron-atom scattering problem. The results of the scattering phase shifts non-relativistic case for this class of potentials are shown to be reasonable compared to analytical results.
Index Terms—Electron-Atom Scattering , Exponential-Cosine Screened Coulomb potential, Hulthén potential, J-Matrix Method , Phase
Shift , Short Range Potentials, and Yukawa potential .
—————————— ——————————
ost of the computational efforts for describing electron scattering have concentrated on quantal methods. The numerical methods used in electron scattering generally
falls into one of two categories, namely perturbation-series expansions based on variations of Born series or the non- perturbative close-coupling approach originating from the expansion of the trial wavefunction into a set of basis func- tions. [1]
Typically, Born- series expansions (Born approximation, dis- torted wave approximation…) [2] used successfully for high collision energies where the projectile-target interaction is a relatively small perturbation of the free-particle motion with large kinetic energy. On the other hand, close-coupling expan- sions were applied to simulate low-energy collision where the incident energy is such that only elastic scattering, or at most excitation of few low-lying target states is possible. However, this method may be extended to deal with higher collision energies.
Close-coupling expansions can be generalized to a relativistic
Hamiltonian can be tridiagonalized in a certain complete set of (L2) basis functions. The resulting symmetric three-term recur- sion relation for the expansion coefficients of the unperturbed wave function is solved in terms of appropriate orthogonal polynomials. The method yields exact scattering information over a continuous range of energy for a model potential ob- tained by truncating the given short-range potential in a finite subset of this basis [4].
This method has been applied successfully to a large number of problems. It is shown to be free from the fictitious reso- nances that plague some algebraic variational scattering methods. The group-theoretical foundation of the theory has been exploited to account for the class of analytic potentials that are compatible with the formalism.
In our calculations we consider a class of short range poten- tials which are exponentially small in the asymptotic domain
r
framework, and the collision problem essentially consists of
V ( r ) O (e ) ,
0 ,
for r (1)
finding the solution to this system. This can be achieved by various iterative, noniterative, or algebraic methods such as R- matrix, and J-matrix. [1, 3].
Through our consideration, it will be applicable to most of the
potentials belonging to this class. We will illustrate our calcu-
lations by considering three specific potentials in detail [5].
Those potentials are the Yukawa potential,
V (r ) Z exp(r ) / r
(2)
The J-matrix theory of quantum scattering is an algebraic
The Exponential-Cosine Screened Coulomb potential,
method which exploits the fact that the unperturbed reference
————————————————
1. Faculty of Science, School of Physics, Duhok University, Duhok, Iraq. . E-mail: : nawzat@uod.ac
V (r ) Z exp( r ) cos(r ) / r
And Hulthén potential,
V (r ) Z exp( r ) / (1 exp( r))
Those potentials have the behavior
(3)
(4)
2. Faculty of Science, School of Physics, Duhok University,
V (r ) ] 1 / r
for r 0
(5)
Duhok, Iraq. E-mail badel_hyder@yahoo.com
And are exponentially small in the r limit, Where![]()
Z : is the atomic number.
: is the screening parameter ( o Z 1 3 , o 0.97 ) [6].
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 2
ISSN 2229-5518
r : is relative distance between the target and the projectile.
complete ( L ) basis
V (r ) Z exp( r ) / r
V (r ) Z exp( r ) cos( r ) / r
] V (r ) Z / r ,
for r 0
V N : is the approximated potential expanded in the basis
The exact solution of the new problem [3 ,8, 10, 12, 13, 14,
15, 16] , i.e.,(equation 6) is:
V (r ) Z exp( r ) / (1 exp( r))
Figure (1) shows the behavior of this class of potentials as a function of r . It is clear that for r 0 this class of potentials
N S t C
Which can be expanded in the basis
N 1
{ l }as:
behaves like a Coulomb potential, whereas for large values of
r they decrease exponentially [5,7].
N ( r ) al l S ( k , r ) t
n 0
C ( k , r )
(7)
t is an approximation

N
of the tangent of the sought phase shift of the exact solu-
tion N of the eq(6)
E
which is equivalent to:
N 1
N (r ) a l l (s l tan c l ) l
(8)
n 0
n 0
The solution has to satisfy the boundary condition
N sin( kr l / 2) tan
cos( kr l / 2) , as r
E N
The left-hand side projection of Eq. (6) onto the basis{ l } gives
then infinitely equations depending on n .![]()
![]()
![]()
![]()
l N 2 N
( H V
k / 2) 0
m 0, 1, ...........,
(9)
Schematically, these equations look like
0 N 1

0 X X X X X
d 0
0
l
X X X X X
X X X X X
0
d1
.
0
0
Fig. 1. The behavior of Yukawa, Hulthén and Exponential-Cosine
Screened Coulomb potentials as a function of r , compared to
X X X X X
.
.
N 1
l
coulomb potential.
X X X X X X
d
N 1
.
(10)
X X X
s l t c l
.
l
l
X X X
sN 1
t N cN 1
.
0 X X X
s l t c l
.
.
. .
.
. .
The basic approach of the J-matrix method is to treat an un- coupled Hamiltonian ( Ho ) exactly in the space spanned by the complete ( L ) basis, in atomic and nuclear scattering. It is
Equation (9) imposes a restriction on
often desirable to use Laguerre or gauss functions as complete
( L ) basis. This leads to a soluble Jacobi matrix. The properties
2
for each m , m 0,1, ...,
E

al 0
of the Jacobi matrix representation of
Ho in the
( L )
basis
(J V)0,0
................... (J V)0,N2
(J V)0,N1
0
play a central role in the J-matrix method. For this reason, this
(J V)1,0 ................... (J V)1,N2 (J V)1,N1 0
l 0
1
method is called the `Jacobi (or J -) matrix method` [8, 9, 10, 11,
12].
...................
The remaining part of the Hamiltonian (i.e., the potential) is
(J V) ................... (J V) (J V) 0
al
0
N2,0
N2,N2
N2,N1
N2
approximated
V approx such that the resulting Hamiltoni-
l
l al
JN1,NsN
an ( Ho V approx ) is also exactly soluble in the complete ( L2 )
(J V)N1,0
................... (J V)N1,N2
(J V)N1,N1
JN1,NcN
![]()
N1
space. Then phase shifts can then be extracted from the result-
0 ................... 0
J ,N 1
JN,N1cN1
![]()
t
J sl
ing wave function E .
N N
N,N1 N1
( Ho V N
k 2
/ 2) N 0
(6)
E
Where
Notice that the large N N
block of the coefficient matrix is
Ho : is the partial-wave reference Hamiltonian expanded in
composed of the matrix elements of
( Ho V
k / 2)
in the
l IJSER © 2013
![]()
{hntt}p://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 3
ISSN 2229-5518
first N basis functions.
To perform a calculation, we need merely augment this
TABLE 1
THE VALUE OF THE PHASE SHIFT FOR THIS CLASS OF POTENTIALS COM-
N N
matrix with the extra row and column shown and
PARED TO THE COULOMB POTENTIAL FOR THE SAME ENERGY
(Z=1,Λ=1,Κ=1,E=1HARTREE, GAUSS BASIS ,N=50, ro =0.0001 A.U.)
with the right-hand side driving term. Equation (10) can be
immediately solved for t by standard techniques. An illumi-
nating formula for tan t can be obtained by prediagonaliz-
ing the inner N N matrix ( Ho V
k / 2) , with the energy-
independent transformation , where
l l
tan
s
![]()
N 1
g
N 1, N 1
( E ) J s
N , N 1 N
(11)
N l l
c
N 1
g
N 1, N 1
( E ) J c

N , N 1 N
Where g
E
N 1
(
/ E E )
with the matrix
N 1, N 1 ( )
n 0
N 1, m m
diagonalizing the finite-dimensional problem
( P ( Ho V k
/ 2) P )m n ( Em E ) m n
.[4, 8, 12, 16, ,17]
In order to visualize the effect of increasing the number of base N (i.e. N ) on the phase shift value , it is necessary to plot the phase shift versus the number of basis N to show that as the number of basis increase N (i.e. N ) ,the phase shift (i.e. t ) converges to correct value (i.e.
t tan as N ) .
The values of the parameters used in the numerical computa-
tions are the energy of the projectile electron e=1 Hartree, po- tential truncation (cut-off parameter) ro =1 a.u, atomic number of the target atom Z =1, potential screening parameter =1, base function scaling parameter =1, numbers of base func- tions N extend from 1 to 550 , and orbital angular quantum number l = 0, 1 .
Since the phase shift has been calculated by using J-matrix
method for Coulomb potential and they are identical to the
analytical results [14, 12, 17], so taking
r 0 the phase shift
Fig.(2.a) Convergence of the non-relativistic phase shift versus number
of Laguerre basis function used to truncate Hulthén potential ( l =0, 1)
of this class of potentials using J-matrix method should con-
verges to that of Coulomb calculated by the same method,
Table (I) shows the value of the phase shift for this class of
potentials compared to the Coulomb potential for the same energy (Z=1,λ=1,κ=1,e=1Hartree, gauss basis ,N=50, ro =0.0001 a.u.)
Figures (2.a), and (2.b) illustrate the nonrelativistic phase shift convergence using Laguerre and Gauss basis function respec-
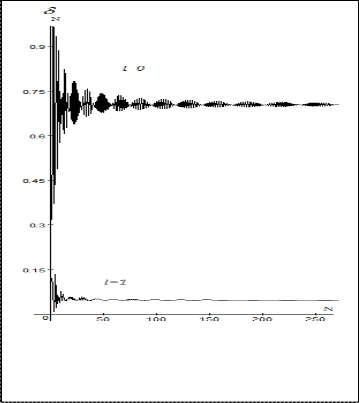
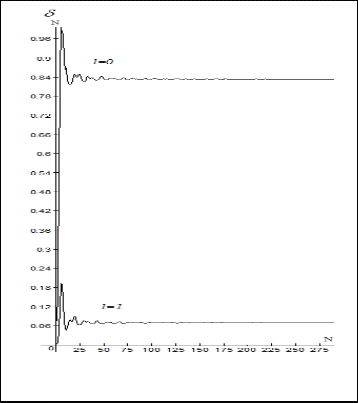
Figures (3.a), and (3.b) illustrate the nonrelativistic phase shift convergence using Laguerre and Gauss basis function respec- tivelly to truncate Exponential- cosine screened coulomb po- tential for l =0 and 1.
The figures show the effect of increasing the number of basis
tivelly to truncate the potential Hulthén for l =0 and 1.
N on the phase shift value N
such that as the number of ba-
The figures show the effect of increasing the number of basis
sis increase the accuracy of the phase shift increase and the
N on the phase shift value N
such that as the number of
convergence become faster.
basis increase the accuracy of the phase shift increase and the convergence become faster.
For l =1 the convergence of phase shift value for Laguerre is faster than that for l =0 especially for N > 50, while for Gauss it convergence at N < 100.
One can notice that the convergence in Laguerre basis set has completely different nature if compared to convergence in Gaussian set. The convergence in Laguerre set appears to be more stable and regular, but is slower. In Gaussian basis, we have rather a quick convergence, but the numerical results “jump” around the analytical result.
For l =1 the convergence of phase shift using Lagurre basis
function is faster than that for l =0 especially for N < 75 which
is the same number of Gauss basis function nedded to achive
the convergence.
One can notice that the convergence in Laguerre basis set has completely different nature if compared to convergence in Gaussian set.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 4
ISSN 2229-5518
Fig.(2.b) Convergence of the non-relativistic phase shift versus num- ber of Gauss basis function used to truncate Hulthén potential ( l =0,
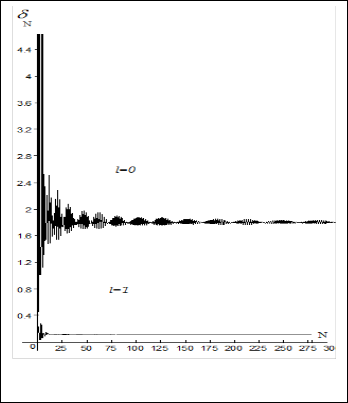
For phase shift convergence in Yukawa potential, figures (4.a) , and (4.b) show the nonrelativistic case using Laguerre and Gauss basis function to truncate the potential for l =0 and
1 recectivily .
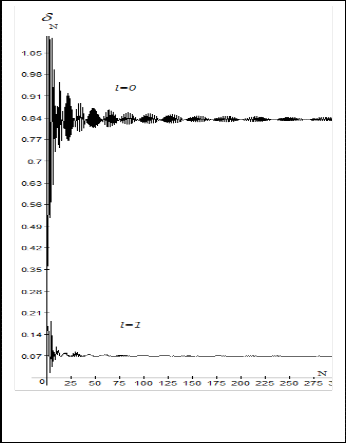
For l =1 the convergence of phase shift value is faster than that for l =0 especially for N < 50 unsing Lagurre while for Gauss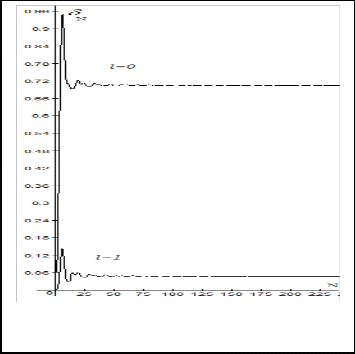
basis function the convergence is N < 50 .
Fig.(4.a) Convergence of the non-relativistic phase shift versus number of Laguerre basis function used to truncate Yukawa potential ( l =0, 1)
In general, in both investigated cases ( l =0 and 1) it is not dif- ficult to see that phase shifts computed numerically converge to phase shift obtained using an analytical formula, the con- vergence in this basis is rather slow but systematic.
Fig.(3.a) Convergence of the non-relativistic phase shift versus num- ber of Laguerre basis function used to truncate Exponential- cosine screened coulomb potential ( l =0, 1)
Fig.(3.b) Convergence of the non-relativistic phase shift versus number of Gauss basis function used to truncate Exponential- cosine screened coulomb potential ( l =0, 1)
IJSER ©
International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 5
ISSN 2229-5518
roughly three times as many are needed to achieve the same accuracy,
As the angular momentum quantum number l increases, the convergence of the scattering phase shift values become faster
in both Laguerre and Gaussian basis because this increasing makes the basis decay faster due to the (r) dependence in the exponent in the both basis,
As the angular momentum quantum number l increases, the effect of the repulsive centrifugal potential increases and be-
come more dominants, so phase shift values decrease.
The convergence of phase shift values for Hulthén potential
are slower than those of Yukawa and Exponential Cosine- Screened Coulomb potential because the fall off of Hulthén potential is slower than that of the other potentials.
[1] N. Anderson, K. Bartschat, Polarization, Alignment, and Orientation in
Atomic Collision, Springer Verlag, New York (2001)
[2] I. Ladawa, Aspect of Atomic Structure in Atomic Collisions, Ph.D. Thesis, University of Bergen (2000).
[3] A. D. Alhaidari, H. Bahlouli, M. S. Abdelmonem, F. S. Al-Ameen and T. H.
Al-Abdulaal, Scattering theory with a natural regularization: Rediscovering the J-matrix method, Physics Letters A, 364.5, 372, (2007
[4] A.D. Alhaidari, H.A. Yamani, and M.S. Abdelmonem, J-matrix method of
L2
scattering in any
basis ,Phys. Rev. A ,64, 042703, (2001)
Fig.(4.b) Convergence of the non-relativistic phase shift versus number of Gauss basis function used to truncate Yukawa potential ( l =0, 1)
Applying the J-matrix method to a class of short range poten- tials for describing the scattering phenomena was the funda- mental purpose of the work. For this purpose the JMATRIX program is modified and used to carry out numerical calcula- tions for scattering phase shifts for potentials in the shape of the Yukawa potential, Hulthén potential and exponential- cosine screened potential. Preformed calculations of scattering phase shifts show, that:
The J-matrix method is an effective method for describing the scattering phenomena for any scattering potential vanishing faster than the Coulomb one given in analytical form (short range potential) and especially for this class of short range potentials(Yukawa potential, Hulthén potential and exponen- tial-cosine screened potential),
The convergence in Laguerre basis set has completely different nature if compared to convergence in Gaussian set. The con- vergence in Laguerre set appears to be more stable and regu- lar, but is slower. In Gaussian basis, we have rather a quick convergence, but the numerical results `jump` around the ana- lytical result. The difference between the Laguerre and Gauss- ian basis is in the "r" The Gaussian basis squares the "r" [see table I] so the (r) dependence in the exponent in the Gaussian basis is a poorer representation than that of the Laguerre basis. Gaussian basis also falls off more rapidly with distance than Laguerre basis. These factors suggest that more Gaussian basis are needed to form a suitable basis set than Laguerre basis,
[5] S.H. Patil , U.I. patil, Asymptotically correct basis for a class of short range potentials, Physica Scripta, 48, 641, (1993)
[6] B. H. Alias, E. M. Ahmad, Energy Calculation of S-State for some Atoms using Hulthén and exponential Cosine Screened Coulomb Potentials, J.Edu.Sci. 34, 45 (1998)
[7] H. A. Yamani, The J-matrix reproducing kernel: Numerical weights at the
Harris energy eigenvalues, J. Math. Phys., 25, 317, (1984)
[8] E. J. Heller and H. A. Yamani, New L2 approach to quantum scattering:
Theory, Phys. Rev. A, 9, 1201, (1974)
[9] E. J. Heller and H. A. Yamani, J-matrix method: Application to s-wave elec- tron-hydrogen scattering, Phys. Rev. A, 9, 1209, (1974)
[10] H.A. Yamani, L. Fishman, J. Math. Phys., J-matrix method: Extensions to arbitrary angular momentum and to Coulomb scattering, 16, 410 (1975)
[11] J.T. Broad and W. P. Reinhardt, J-matrix method: multichannel scattering and photoionization, J. Phys., B, 9, 1491 (1976)
[12] P. Syty, The J-matrix method: numerical computations, TASK Quarterly 3
No. 3 (1999)
[13] S. K. Adhikari, Variational Principles and the Numerical Solution of Scatter- ing Problems, John Wiley & Sons, Inc., New York (1998)
[14] P. Horodecki, Relativistic J-matrix method, Phys. Rev. A, 62, 052716 (2000)
[15] A. D. Alhaidari, H. A. Yamani, and M. S. Abdelmonem, Relativistic J-matrix theory of scattering, Phys. Rev. A, 63, 062708,(2001)
[16] H. A. Yamani, The J-matrix reproducing kernel: Numerical weights at the
Harris energy eigenvalues, J. Math. Phys., 25, 317, (1984)
[17] P. Syty, Programming the J-matrix method, MSc thesis, Gdansk University of
Technology (1999)
IJSER © 2013 http://www.ijser.org