International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2257

ISSN 2229-5518

Performance of RCC Box type Superstructure in

Curved bridges

MULESH K. PATHAK (M. E. CASAD)

LECTURER IN APPLIED MECHANICS DEPARTMENT GOVERNMENT POLYTECHNIC, VALSAD- 396001

Contact No.- 09725609699 E-mail : muleshp@yahoo.com
In this paper, various behaviours like bending, shear, axial & torsion are presented for horizontally curved RCC box bridges considering 3-D FEM using SAP software. FEM models are prepared for four different span lengths keeping the same material properties with varying degree of curvature from 0° to 90° for different load conditions & combinations to get multiplication factor for various actions like BM, SF, AF & TM w.r.t to straight bridge to multiply the desired parameters of straight bridge to get that for curved bridge. This approach simplifies analysis & the preliminary design of curved bridge section.

IJSER

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2258

ISSN 2229-5518

1.0 INTRODUCTION

Horizontally curved bridges are the most feasible options at complicated interchanges or river crossings where geometric restrictions and constraint of limited site space, make difficult the adoption of standard straight superstructures. Usually these bridges are of cellular cross- section so that high torsional moment can be well resisted economically. Contrary to straight bridges, a very limited documentation on the study of horizontally curved bridges has been available.
In the current specifications of IRC, no separate guideline is available for the curved bridge except consideration of torsion moment. Refined analysis is required to calculate torsional moment in the curved bridges. Finite element method is most suitable for analysis of such type of problem, but looking to the complexity involved in use of finite element method, the designer involved in the process of bridge designing need some simplified solution to solve the problem. In this paper, the authors have tried to solve the problem by introducing the term multiplication factor (M.F), which is used to find out desired action in the curved bridge by simply multiplying to the corresponding action of the straight bridge.
Ali R. Khaloo1 and M. Kafimosavi2 has discussed about enhancement of flexural design of
horizontally curved prestressed bridges1. The flexural behavior of horizontally curved prestressed (post tensioned) box bridges in studied by using three dimensional and refined finite element modeling and analysis. The results of analysis show that in curved bridges, stress distribution is significantly different in comparison to straight bridges. Also, the level of stresses at some locations of section width is considerably high.
There is a very limited knowledge available about flexural behavior of curved bridges, both in standard specifications and literature. In the present scenario, engineers often resort to straight bridge analysis for a span with minor curvature in plan. In this paper, analytical results of straight and curved bridges are compared and charts and tables are prepared for a various parameters such as shear, bending, torsion and axial force for curved bridges. This type of work can be also useful for preliminary design of horizontally curved bridge considering straight bridge analysis with multiplication factor for various parameters like degree of curvature, span etc.
Hence to fill in the void for the realistic analysis, the work on the parametric study of curved bridges is performed. Various behaviors like bending, shear, axial and torsional of horizontally curved RCC box bridges is presented by using three-dimensional finite element analysis software, SAP 20005. Fourty models are prepared for four different span lengths (15m, 20m, 25m & 30m) keeping the same material properties with varying degree of curvature from 0° to 90° at 10° increment for different load conditions and load combinations. Charts & tables for various parameters of curved bridges are presented in this paper.

2.0 FINITE ELEMENT METHOD

The main advantage of this method is its universal acceptance for variety of problems. The method over other analytical techniques is its generality. Normally, as was pointed out, it seems possible, by using many elements, to virtually approximate any continuum with complex boundary and loading conditions to such a degree that an accurate analysis can be expected. The application of FEM to bridge problems will need a thorough understanding and

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2259

ISSN 2229-5518

knowledge of almost all the facets of advanced structural mechanics and numerical techniques which many times a design engineer may not have.
During the past two decades, the Finite Element Method (FEM) 6 of Analysis has rapidly become a very popular technique for the computer solution of complex problems in engineering. The FEM consists of solving the mathematical model which is obtained by idealizing a structure as an assembly of various discrete two or three dimensional elements connected to each other at their nodal points, possessing an appropriate number of degrees of freedom.
The entire structure (Box Girder) is divided into small elements and the stiffness of the structure is assembled from the membrane and plate bending stiffness of each element8. The method is the only one that is truly general and powerful and can handle all types of structures

3.0 MODEL USING SAP- 2000 SOFTWARE

SAP5, product of Computer and Engineering Software and Consulting, has been proven to be the most integral, productive and practical general purpose structural program in the market today. SAP has a three dimensional interface and uses finite element method for analysis. SAP is a stand-alone finite element based structural program for the analysis and design of structures. It has powerful user interface with many tools to aid in the quick and accurate construction of models, along with the sophisticated analytical techniques needed to do the most complex projects.
In SAP, there is an option of bridge wizard section, which is useful to create model easily &
quickly. There are 12 steps in SAP to create a bridge model, which are given below.
1) Layout lines: Layout lines are used as reference lines for defining the vertical and horizontal layout of bridge objects and lanes. Layout lines are defined in terms of stations, bearings and grades. The lines may be straight, bent or curved both in the horizontal and the vertical plane. There are many choices available for both Horizontal and Vertical curves. In this work the Right Curve line in Horizontal case is selected.
2) Deck sections: Various parametric bridge deck sections are available for use in defining a bridge. In this work the Concrete Box Girder External Girders Sloped option is selected shown in Fig. 1. Shows the various bridges deck sections type.

Figure 1. Cross Section for Box Girder

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2260

ISSN 2229-5518

3) Abutment definitions: Abutment definitions specify the support conditions at the ends of the bridge. The user support condition allows each of the six degrees of freedom at the abutment to be specified as fixed, free or partially restrained with a specified spring constant.

4) Bent definitions: Bent definitions specify the geometry and section properties of the bent cap beam and the bent columns. They also specify the base support condition of the bent columns.

5) Diaphragm definitions: Diaphragm definitions specify properties of vertical diaphragms that span transverse across the bridge. Solid concrete diaphragm properties are onl y applicable to concrete bridge sections. For all models, the end diaphragm thickness is kept the same as 0.4 m, in order to reduce local effects and provide uniform distribution of large support reaction.

6) Hinge definitions: Hinge definitions specify properties of hinges (expansion joints) and restrainers.
7) Parametric variations: Parametric variations defined the variations in the deck section along the length of the bridge. Any parameter like varying the bridge depth, thickness of girders, slabs along the length of the bridge etc. can be used in the parametric definition of the deck section that can be vary. One or more of the parameters can vary at the same time. Each varying parameter can have its own unique variation. The variations may be linear, parabolic or circular.
8) Bridge object: The bridge object is the heart of the bridge modeler. The following is included in the Bridge objects definitions: (a) The bridge spans are defined (b) Deck section properties are assigned to each span (c) Parametric deck section variations may be assigned to each span (d) Abutment properties and skews are assigned (e) Bent properties and skews are assigned (f) Hinge locations, properties and skews are assigned (g) Super elevations are assigned (h) Prestressed tendons are defined.

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2261

ISSN 2229-5518

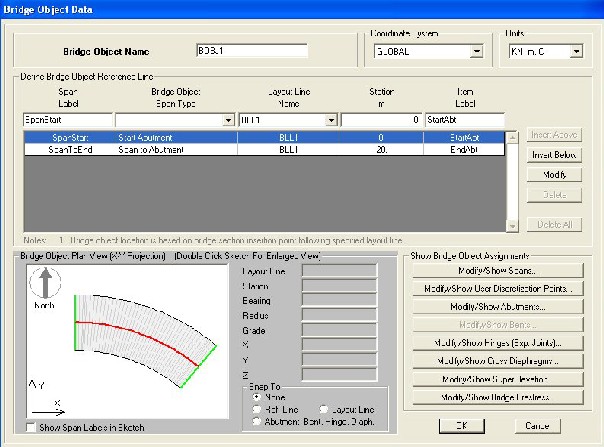
Figure 2: Bridge Object menu of SAP2000 software

9) Update linked model: The update linked model command creates the SAP2000 object-
based model from the Bridge objects definition. Bridge object menu of SAP2000 software is shown in fig. 2. Spine models, area object models (Shell Element) and solid object models of the bridge can be created when the linked model is updated.
10) Lanes: Lanes must be defined for the analysis of the bridge for moving vehicle live loads. Lanes can be defined with reference to either layout lines or existing frame objects. A Single lane is referenced to one or more layout lines or one or more frame objects. Lanes can be defined with width if desired. Lanes are used in the definition of Moving Load type analysis cases and in Bridge Live load cases. In this paper, lanes for various load cases are shown in fig. 3 (As per SAP input).

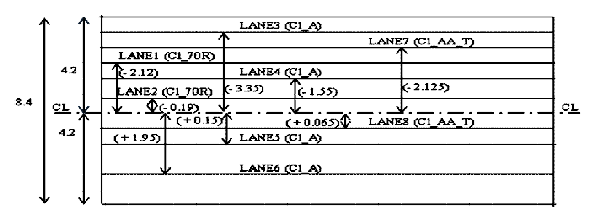
Figure 3: Lanes Defined for Different Load Cases

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2262

ISSN 2229-5518

11) Vehicles: Vehicles must be defined to analyze the bridge for vehicle live loads. In SAP2000 v11 vehicles loads are applied to the structure through lanes. Numerous standard vehicle definitions are built into the program. In addition the General Vehicle feature can be used to create one’s own vehicle definition. Each vehicle definition consists of one or more concentrated and/or uniform loads. The software SAP 2000 v11 also consist of IRC standards of loading.
12) Analysis case: There are many load cases needs to be considered while analyzing bridges. Several analysis options are available especially for analysis of vehicle live loads. Moving load analysis cases compute influence lines for various quantities and solve all permutations of lane loading to obtain the maximum and minimum response quantities. Multi-step static and multistep dynamic (direct integration time history) analysis cases can be used to analyze one or more vehicles moving across the bridge at any speed. These multi-step analysis cases are defined using special Bridge Live Load Cases that defined the direction, starting time and speed of vehicles moving along lanes.

The Finite element model is prepared using bridge wizard of SAP-2000 software is shown in fig.4. The 4 noded 3D shell elements are taken in modeling of box section. The results of the finite element models with different mesh sizes are compared and finally 1.25 m2 mesh size is adopted in the modeling of structures.

IJSER

Figure 4: Three Dimensional model of 30 m span and 60° curvature in SAP software

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2263

ISSN 2229-5518

4.0 PARAMETRIC STUDY

In the present paper, two parameters, which are having highest influence on behaviour of the curved bridges, are considered. These parameters are as follows:
1) Span: This is important parameters for any bridge structure. From the literature, it is found that RCC Box type of superstructure be cost effective in the range of 15 m. to 30 m. and hence in this study span length ranging in this limit with an increase in 5 m., i.e., 15 m., 20 m., 25 m. and 30 m., and its effect on various behaviour of the curved bridge is presented in this paper.
2) Degree of curvature: This is most important parameter for curved bridge structure from the behavior point of view. In addition to the axial, flexure and shear stresses, torsional stresses are found to be significant in the curved bridges and hence this effect is studied by varying degree of curvature from 0° to 90° with increment of 10°.
Fourty models of curved RCC box girder are prepared by varying span of 15m, 20m, 25m and 30m and degree of curvature from 0° to 90° with 10° increment for different load conditions and load combinations. Various parameters like bending, shear, axial and torsional behavior of curved RCC box bridges are presented using three-dimensional finite element modeling and analysis software, SAP 2000 and charts & tables are prepared and few of them are presented in this paper for above mentioned parameters of curved bridges.

5.0 PROBLEMIDESCJRIPTIONSER

The parametric study is carried out on a problem of curved bridges of two lanes with main
carriageway width of 7.5m having RCC box type superstructure with span length of 15 m., 20
m., 25 m. and 30 m. and degree curvature from 0° to 90° with 10° increment. The material properties are kept same while different cross section of the box type superstructure is adopted for each span length. Support conditions simulate a simple span with one end of pinned support and the other end roller allowing horizontal movement. Super elevation of 7% is provided for all models to counteract the effect of centrifugal force in the curvature. End diaphragms of 0.4 m width are provided, in order to reduce local effects and provide uniform distribution of large support reaction.

Loads

The following loads are considered3:
1) Dead load: The dead load includes self weight of the box type superstructure.
2) SIDL: Weight of crash barrier and wearing coat is considered in SIDL.
3) Live Load: IRC loading for two lane bridges are considered, which are as follows:

 One lane of Class-70R wheel loading

 Two lane of class-A loading

 One lane of class-AA Tracked loading

4) Load Combination: Following load combinations are carried out and worst effect is considered in the analysis.

 DL + SIDL + LL (Maximum of Class 70R, Class A and Class AA Tracked)

The live load moments are checked at edge and center of the main carriageway with specified minimum clearance as per IRC: 6 and it is found that the live loads at the edges are governing and hence the results of the same have been taken into consideration.

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2264

ISSN 2229-5518

6.0 RESULTS

The results are collected for a particular span (15m, 20m, 25m, and 30m) with varying degree of curvature (0° to 90° at 10° increment) and a particular degree of curvature with varying span. Results are taken for total load i.e. DL + SIDL + LL (Max.). The values of maximum B.M., S.F., Torsion and Axial force are collected for entire Section of which maximum B.M. and axial force occurs at mid span, maximum S.F. at edge and maximum torsion not being exactly at edge but somewhat away from support.

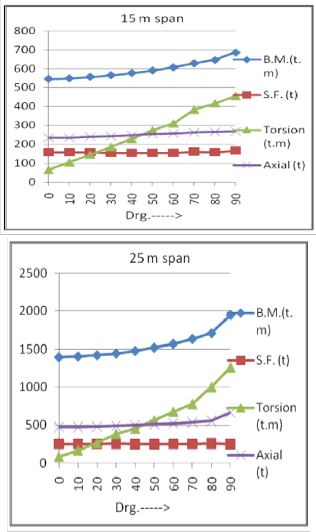
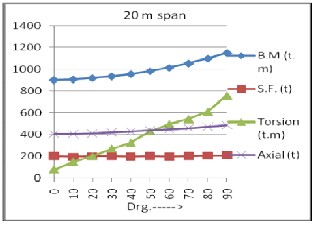
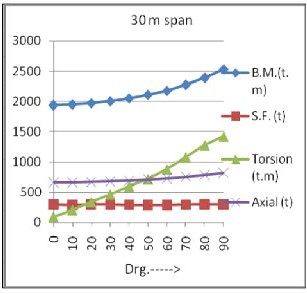
Parametric variation of various actions for 15m, 20m, 25m and 30m span for varying degree of curvature as abscissa for entire box section for combined load case of DL + SIDL + LL (Max.) in a graphical form is shown in fig. 5.

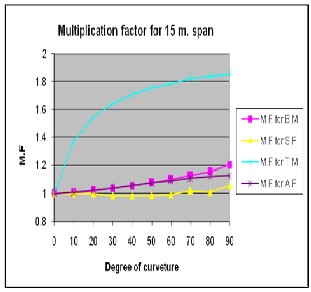
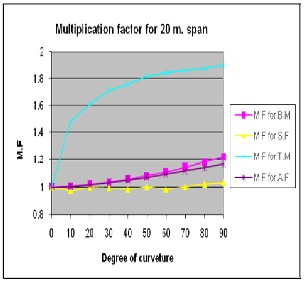
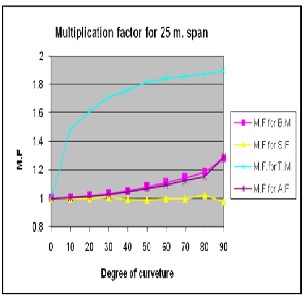
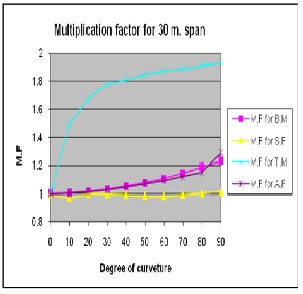
Multiplication factors for B.M., S.F., Axial force & Torsional moment for spans of 15m,

20m, 25m and 30m and for varying degree of curvature for entire box Section for load case of

DL + SIDL + LL (Max.) in a graphical form is shown in fig. 6.

IJSER

Figure 5: B.M., S.F., Axial force & Torsional moment for span of 15m, 20m, 25m and 30m for varying degree of curvature for entire box Section.

IJSER

Figure 6: Multiplication factors for B.M., S.F., Axial force & Torsional moment for spans of 15m, 20m,

25m and 30m and for varying degree of curvature for entire box.

7.0 CONCLUSION

Fourty Models were prepared for four different span lengths (15m, 20m, 25m and 30m) keeping the same material properties with varying degree of curvature from 0° to 90° at 10° increment for different load conditions and load combinations. Loads, load combinations and end conditions were applied to the models as per IRC specifications. Finite element software SAP-2000 was used for the analysis. The conclusions obtained from the present study are shown in tables and graphs above and can be described as below.
1) From the graphs of the results shown above it can be inferred that the increase in the torsion for any set of graph is comparatively steeper than that of bending moments, shear forces and axial carrying capacities which indicates that box section is having higher torsional stiffness and is nonlinearly vary with degree of curvature.
2) The study also provides multiplication factors for all the parameters for varying degree of curvature (i.e. 10° to 90°) W.r.t. a straight bridge (0°) and for varying spans (between 15m to
30m) as shown in fig 6. These can be useful to simplify the analysis by considering straight

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2266

ISSN 2229-5518

bridge instead of curved bridge, in which multiplication factor is used multiply to the corresponding action of the straight bridge. This can be very much useful in the preliminary design of the section.
3) From the study it is observed that for different span, the multiplication factor for variable degree of curvature is varying linearly for axial force & bending moment, which is about 1.2 to 1.3 for 90° curvature. Multiplication factor for torsion moment is varying nonlinearly having 1.8 to 1.9 for 90° curvature, while there is no need to apply multiplication factor for shear force.

REFERENCES

1. Ali R. Khaloo and M. Kafimosavi (2007) “Enhancement of Flexural Design of Horizontally Curved Prestressed Bridges “, Journal of bridge engineering, Vol.12, No.5, September.
2. Barr P. J., Yanadori N., Womack K. C.(2007) “ Live load analysis of a Curved I Girder
Bridge”, Journal of bridge engineering, Vol. 12, No. 4,July.
3. IRC: 6(2000). Standard Specification and Code of Practice for Road Bridge, Section II,
Loads and Stresses, Indian Road Congress, New Delhi.
4. IRC: 21(2000). Standard Specification and Code of Practice for Road Bridge, Section –

III, Cement Concrete (Plain and Reinforced), Indian Road Congress, New Delhi.

5. Bridge Manual, SAP (2000). Linear and Nonlinear Static and Dynamic Analysis and
Design of Three- Dimensional structures.
6. C.S. Surana and R. Agrawal. Griliage Analogy in Bridge Deck Analysis ,Narosa
Publishing House, New Delhi.
7.Magdy Samaan ; Khaled Sennah ; and John B. Kennedy (2005) “Distribution Factors for
Curved Continuous Composite Box- Girder Bridges “ , Journal of bridge engineering, Vol.10,No.6, November.
8. Dr. V.K. Raina. Raina’s Concrete Bridge Practice Analysis, Design & Economics, The international bank for reconsruction and development and The United Nations Organisation.