Where Y = vertical co-ordinate; X = abscissa; and a = shape parameter (Figure 1).
Top width T is given by
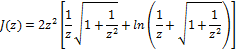
Wetted perimeter, W, is given by where
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 804
ISSN 2229-5518
Parabolic Channel Design
Richwell Mubita Mwiya
The parabolic cross section shape is for many situations the best practical shape for an open channel. One of its
advantages is the ability to maintain a higher velocity at low discharge which reduces the tendency to deposit sediment. Another is its greater depth at low discharges which enables it to carry floating and semi-floating debris more easily than a flat-bottomed channel. Moreover, small parabolic channels tend to suffer less damage from cattle because they do not walk in them, and from cyclists because they do not ride in them as often happens to other conventional channels. Furthermore, Mironenko et. al. ([13]) and Chahar ([5]) stated that since river beds, unlined channels, and irrigation furrows all tend to approximate a stable parabolic shape, unlined channels are made more hydraulically stable when they are initially constructed in a parabolic shape. The channel side slopes along the cross section are always less than the maximum allowable slide slope which occurs at the water surface. Laycock ([11]) also states that in the form of precast concrete segments, the parabola has an inherent structural strength, especially if the sides are unsupported, and practically, it is easy to design the profile of varying thickness so that the strength is at the root of the cantilevered sides, where it is needed.
Loganathan ([12]) and Chahar ([5]) showed that the optimal parabolic cross section has a side slope of 1 / 0.513 at the water surface. However, Laycock ([11]) pointed out that, in order to increase strength and ease of handling, small precast segments must have a narrower top width than the hydraulically most efficient section, and cast-in situ
————————————————
Richwell Mubita Mwiya is currently pursuing masters degree program in Agirculttural Water Soil Engineering at Hohai University, China, PH-8615150573420. E-mail: rmwiya@yahoo.com
concrete channels should have a wider top width to flatten the side slopes for safety reasons and to make construction
without formwork easier. He argued that people and animals have great difficulty getting out of large, smooth- lined channels with side slopes greater than 1/2, and that constructing channels without formwork greatly reduces the construction costs of the channel. Montanes ([14]) also stated that a side slope of 60o (or 1/0.577) is too steep to be stable in most types of ground except rock. Thus, although the most hydraulically efficient parabolic section has a water surface side slope of 1/0.513, often what is needed in the field is a channel which has a surface water side slope less than this value or greater than this value.
Hussein [9], Anwar and Clarke ([1]) and Anwar and de Vries ([2]) suggested methods for the design of power-law channels where the variable to be optimized is the exponent m for the power-law channel and not the side slope at the water surface. However, these tend to produce U-shaped cross sectional designs which tend to lose some of the advantages of the first order parabolic channel.
In this paper, a method is proposed for the design of a first order parabolic channel with consideration of freeboard and maximum allowable side slope. Another method is shown that only considers freeboard and not the maximum allowable side slope. The second method optimizes the channel section using the optimum side slope value at the water surface of 1/0.513. A design example is used to compare the two methods.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 805
ISSN 2229-5518
A parabolic canal is described by the equation ([13],[12],[5]): ![]() (1)
(1)
Where Y = vertical co-ordinate; X = abscissa; and a = shape parameter (Figure 1).![]()
Top width T is given by![]()
![]()
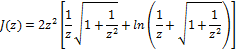
Wetted perimeter, W, is given by where
(6)
(7) (8)
(9)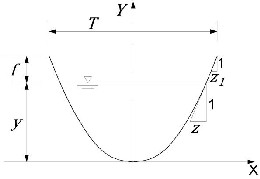
Figure 1 Parabolic channel cross section
It can be shown that the total area At is given by![]()
![]()
and flow area A as
(2)
(3)
Manning’s equation is the most used equation for uniform
flow design of open channels and it is used in this analysis.
The Manning’s equation can be expressed as follows
![]() (10)
(10)
in which Q = flow discharge (m3/s); n = Manning’s
roughness coefficient; and S = longitudinal bed slope (%).
Substituting (3) and (8) into (10) gives
in which y = the flow depth (m); f = freeboard (m); 1/z1 is the side slope at the top bank level, and 1/z is the side slope at the water surface level.
It can also be shown that z1 and z are related by the equation
![]() (4)
(4)
![]()
where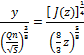
(11)
The LHS of (11) is the nondimensional expression for flow depth ([5]). Thus
![]() (12)
(12)
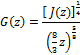
where Y* is nondimensional flow depth and
(13)
Thus flow area A can be expressed as
(5)
TABLE 1 gives values of Y* for different values of z1 and k.
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 806
ISSN 2229-5518
TABLE 1(a)
VALUES OF Y* FOR DIFFERENT VALUES OF z1 AND k![]()
![]()
z1 Y*
![]()
k = 0 k = 0.1 k = 0.2 k = 0.3 k = 0.4 k = 0.5 k = 0.6
0.1 2.7401 2.6616 2.5920 2.5297 2.4735 2.4223 2.3756
0.2 1.8090 1.7595 1.7157 1.6766 1.6413 1.6093 1.5800
0.3 1.4359 1.3986 1.3657 1.3363 1.3098 1.2857 1.2638
0.4 1.2290 1.1987 1.1719 1.1480 1.1265 1.1069 1.0891
0.5 1.0956 1.0698 1.0470 1.0266 1.0083 0.9916 0.9764
0.6 1.0014 0.9788 0.9587 0.9408 0.9247 0.9100 0.8966
0.7 0.9307 0.9104 0.8924 0.8762 0.8617 0.8485 0.8364
0.8 0.8753 0.8567 0.8402 0.8255 0.8121 0.8000 0.7889
0.9 0.8304 0.8131 0.7979 0.7842 0.7718 0.7605 0.7502
1.0 0.7930 0.7768 0.7625 0.7497 0.7381 0.7275 0.7178
1.1 0.7612 0.7460 0.7324 0.7203 0.7093 0.6993 0.6901
1.2 0.7337 0.7193 0.7064 0.6948 0.6844 0.6748 0.6660
1.3 0.7096 0.6958 0.6835 0.6725 0.6624 0.6533 0.6449
1.4 0.6883 0.6751 0.6632 0.6526 0.6430 0.6341 0.6260
1.5 0.6692 0.6564 0.6451 0.6348 0.6255 0.6170 0.6091
1.6 0.6520 0.6396 0.6286 0.6187 0.6097 0.6014 0.5938
1.7 0.6363 0.6243 0.6136 0.6040 0.5953 0.5872 0.5799
1.8 0.6220 0.6103 0.5999 0.5906 0.5820 0.5742 0.5671
1.9 0.6088 0.5975 0.5873 0.5782 0.5699 0.5623 0.5553
2.0 0.5966 0.5855 0.5756 0.5667 0.5586 0.5512 0.5443
2.1 0.5853 0.5745 0.5648 0.5561 0.5481 0.5409 0.5342
2.2 0.5747 0.5641 0.5547 0.5461 0.5383 0.5312 0.5247
2.3 0.5648 0.5545 0.5452 0.5368 0.5292 0.5222 0.5158
2.4 0.5556 0.5454 0.5363 0.5281 0.5206 0.5137 0.5074
2.5 0.5468 0.5368 0.5279 0.5198 0.5125 0.5057 0.4995
2.6 0.5386 0.5288 0.5200 0.5120 0.5048 0.4982 0.4921
2.7 0.5308 0.5211 0.5125 0.5047 0.4976 0.4911 0.4850
2.8 0.5234 0.5139 0.5054 0.4977 0.4907 0.4843 0.4783
2.9 0.5164 0.5070 0.4986 0.4911 0.4842 0.4778 0.4720![]()
3.0 0.5097 0.5005 0.4922 0.4847 0.4779 0.4717 0.4659
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 807
ISSN 2229-5518
TABLE 1(b)![]()
![]()
z1 Y*![]()
k = 0.7 k = 0.8 k = 0.9 k = 1.0
0.1 2.3325 2.2927 2.2557 2.2212
0.2 1.5531 1.5283 1.5052 1.4837
0.3 1.2436 1.2250 1.2078 1.1917
0.4 1.0727 1.0576 1.0436 1.0305
0.5 0.9624 0.9495 0.9375 0.9264
0.6 0.8843 0.8729 0.8623 0.8524
0.7 0.8253 0.8149 0.8054 0.7964
0.8 0.7787 0.7692 0.7604 0.7521
0.9 0.7406 0.7318 0.7236 0.7159
1.0 0.7088 0.7005 0.6927 0.6855
1.1 0.6816 0.6737 0.6663 0.6594
1.2 0.6579 0.6504 0.6433 0.6368
1.3 0.6371 0.6298 0.6231 0.6168
1.4 0.6185 0.6116 0.6051 0.5990
1.5 0.6019 0.5951 0.5888 0.5830
1.6 0.5868 0.5803 0.5742 0.5684
1.7 0.5730 0.5667 0.5607 0.5552
1.8 0.5604 0.5542 0.5484 0.5430
1.9 0.5488 0.5427 0.5371 0.5318
2.0 0.5380 0.5321 0.5266 0.5214
2.1 0.5279 0.5222 0.5168 0.5117
2.2 0.5186 0.5129 0.5076 0.5026
2.3 0.5098 0.5042 0.4990 0.4942
2.4 0.5015 0.4961 0.4910 0.4862
2.5 0.4938 0.4884 0.4834 0.4787
2.6 0.4864 0.4811 0.4762 0.4716
2.7 0.4795 0.4743 0.4694 0.4648
2.8 0.4729 0.4677 0.4629 0.4585
2.9 0.4666 0.4615 0.4568 0.4524![]()
3.0 0.4606 0.4556 0.4510 0.4466
3. Using the chosen z1 and for a chosen value of ko, find the nondimensional depth Y* from table 1.
4. Find the flow depth of the channel section by finding the product of L and Y*.
5. Compute the resulting freeboard fo = koY*.
6. If computed f0 = f, go to (5), else, set k1 = f /Y*, start at
(3) and repeat.
7. Compute flow area using (6); z using (4); wetted perimeter using (8) and (9); total cross sectional area using (2); and top width using (7).
8. End
Mironenko et. al [13] gives values of z1 for different materials; Laycock ([11]) gives values of freeboard for different normal flow discharges; and Cuenca (1989) gives values of Manning’s roughness coefficient n for different types of lining materials.
In line with Loganathan ([12]), minimize total area At
![]() (14)
(14)
subject to
![]() (15)
(15)
![]()
in which
(16)
The design procedure of an open channel is often an iterative one. For a given specific project, the design
procedure can be summarized in the following steps:
1. Choose the Manning’s roughness coefficient n, allowable maximum side slope 1/z1 for the particular type of lining, and freeboard required.![]()
2. For the given Q and So, and chosen n, compute the length scale .![]()
![]()
Substituting (15) into (14) gives in which
and
IJSER © 2013 http://www.ijser.org
(17)
(18)
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 808
ISSN 2229-5518
![]() (19) Flow depth in (15) can be expressed in nondimensional
(19) Flow depth in (15) can be expressed in nondimensional
form as
Design a parabolic channel section to carry 1.0 m3/s of water. The channel will be built in a firm clay soil with a
longitudinal slope of 0.1% and will have n = 0.035.
![]()
in which
(20)
(21)
Iteration 1:
(1) From Mironenko ([13]), z1 = 1.5 for firm clay soil. From Laycock ([11]), f = 0.5 m; (2) L = 1.0388; (3) assuming ko = 0.3, Y* = 0.6348; (4) y = L * Y* =1.0388 * 0.6348 = 0.66 m; (5) fo = ko *
Eq. (17) reaches its unconstrained minimum at z = 0.514 for any given k. Thus, the unconstrained nondimensional values for flow depth, flow area, and wetted perimeter of the optimal parabolic channel section are:![]() (22) It can be shown that T* is given by the equation:
(22) It can be shown that T* is given by the equation:
![]() (23)
(23)
The design procedure for an optimal parabolic channel section can be summarized as follows:
1. For the required discharge Q and given longitudinal slope S, choose the Manning’s roughness coefficient n, and freeboard required.
2. Compute the length scale ![]() .
.
3. Compute flow depth y = 1.08388 * L.
4. Compute k = f / y.
5. Compute z1 using (4) and z = 0.514 .
6. Compute flow area using (6), total area using (2), wetted perimeter using (8) and (9), top width using (7), and total depth h = f + y.
7. End
The example used by Mironenko et. al. ([13]) is used here. The problem is re-phrased as:![]()
y = 0.3 * 0.66 = 0.20 m; (6) fo ![]() f
f
Iteration 2:
(3) k1 = f / y = 0.5 / 0.66 = 0.8, Y* = 0.5951; (4) y = L * Y* =1.0388
*0.5951 = 0.62 m; (5) f1 = k1 * y = 0.8 * 0.62 = 0.47 m; (6)
Because f1![]() f, the iteration is terminated at this point. (7) A =
f, the iteration is terminated at this point. (7) A =
2.06 m2 ; z = 2.0; W = 5.16 m; At = 5.02 m2; T = 6.70 m.
(1) Q = 1.0 m3/s, S = 0.1%, n = 0.035, f = 0.5 m; (2) L = 1.0388; (3) y = 1.0806*1.0388 = 1.12 m (4) k = 0.5 /1.12 = 0.446 (5) z1 =
0.427 (5) A = 1.6003 * 1.03882 = 1.73 m2, At = 2.78 m2, W =
3.2400 * 1.0388 = 3.37 m, T = 2.77 m.
It is clear that the results of example (2) are more optimal than the results of example (1). Flow area, wetted perimeter, top width and total cross sectional area obtained by the first method are all larger than those obtained by the second method.
Several methods have been developed for the design of optimal parabolic channels. However, rarely has maximum and, in some cases, minimum allowable side slopes been taken into account even though in practice there is often need to take this design parameters into consideration. Sometimes the side slope is chosen based on the angle of repose of material for better stability or for vehicles to cross the channel during no-flow periods ([5]). Also, improving strength and ease of handling of small precast segments is done by deliberately making the side slopes steeper. Furthermore, safety is enhanced to both animals and people by making side slopes of large channels as flat as possible. Thus the value of side slope maybe be predetermined and has to be taken into consideration in the design process. This paper has proposed a method by which this problem
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 809
ISSN 2229-5518
can be addressed. However, the proposed method results in a non-optimal section as shown by comparing the results
of the two methods. This is because the side slope parameter z is the governing parameter for a parabola and when this parameter is prevented from assuming its optimal value of 0.514 at the normal flow depth, the section obtained is less optimal.
[1] A. A. Anwar and D. Clarke, “Design of Hydraulically Efficient Power-Law Channels with Freeboard.” J. Irrigation and Drainage Engineering, vol. 131, no. 6, pp. 560-563, Dec.
2005.
[2] A. A. Anwar and T. T. de Vries, “Hydraulically efficient
powerlaw channels.” J. Irrigation and Drainage
Engineering, vol. 129, no. 1, pp. 18–26, Feb. 2003.
[3] S. L. Atmapoojya and R. N. Ingle, “Discussion of
‘Optimal design of parabolic-bottomed triangle canals,’
by K. Babaeyan-Koopaei, E. M. Valentine, and D. C.
Swailes.” J. Irrigation and Drainage Engineering, vol. 128,
no. 3, pp. 189–191, Nov/Dec 2002.
[4] K. Babaeyan-Koopaei, E. M. Valentine D. and C.
Swailes, “Optimal design of parabolic-bottomed
triangle canals.” J. Irrigation and Drainage Engineering,
vol. 126, no. 6, pp. 408–411, Nov. 2000.
[5] B. R. Chahar, “Optimal Design of Parabolic Canal
Section.” J. Irrigation and Drainage Engineering, vol. 131,
no. 6, pp. 546-554, Dec. 2005.
[6] V. T. Chow, Open-channel hydraulics. McGraw-Hill, New
York, 1959.
[7] R. H. Cuenca, Irrigation system design; an engineering
approach. Prentice- Hall, Inc., Englewood Cliffs, N.J.,
pp. 464-517, 1989.
[8] C. Guo and W. C. Haughes, “ Optimum channel cross
section with freeboard.” J. Irrigation and Drainage
Engineering, vol. 110, no. 3, pp. 304-314, Sept. 1984.
[9] A. S. A. Hussein, “Simplified Design of Hydraulically
Efficient Power-Law Channels with Freeboard.” J. Irrigation and Drainage Engineering, vol. 134, no. 3, pp.
380-386, Jun. 2008.
[10] A. R. Kacimov, “Discussion of ‘Hydraulically efficient
powerlaw channels’ by Arif A. Anwar and Tonny T. de
Vries.” J. Irrigation and Drainage Engineering, vol. 130, no. 5, pp. 445–446, Jan /Feb 2004.
[11] A. Laycock, Irrigation Systems: Design, Planning and
Construction. CAB International, Cambridge, 2007.
[12] G. V. Loganathan, “Optimal Design of Parabolic
Canals.” J. Irrigation and Drainage Engineering, vol. 117, no. 5, pp. 716-735, Sept/Oct 1991.
[13] A. P. Mironenko, L. S. Willardson and S. A. Jenab, “Parabolic canal design and analysis.” J. Irrigation and Drainage Engineering, vol. 110, no. 2, pp. 241–246, Jun.
1984.
[14] J. L. Montanes, Hydraulic Canals: Design, construction, regulation and maintenance. Taylor & Francis, New York,
2006.
[15] T. S. Strelkoff and A. J. Clemmens, “Approximating wetted
perimeter in power-law cross section.” J. Irrigation and
Drainage Engineering, vol. 126, no. 2, pp. 98–109, Mar/Apr
2000.
IJSER © 2013 http://www.ijser.org