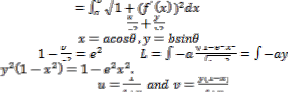International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 467

ISSN 2229-5518

Overview of History of Elliptic Curves and its use in cryptography

Minal Wankhede Barsagade, Dr. Suchitra Meshram

Abstract— Elliptic curves occur first time in the work of Diophantus in second century A.D. Since then the theory of elliptic curves were studied in number theory. Till 1920, elliptic curves were studied mainly by Cauchy, Lucas, Sylvester, Poincare. In 1984, Lenstra used elliptic curves for factoring integers and that was the first use of elliptic curves in cryptography. Fermat’s Last theorem and General Reciprocity Law was proved using elliptic curves and that is how elliptic curves became the centre of attraction for many mathematicians.

Properties and functions of elliptic curves have been studied in mathematics for 150 years. Use of elliptic curves in cryptography was not known till

1985. Elliptic curve cryptography is introduced by Victor Miller and Neal Koblitz in 1985 and now it is extensively used in security protocol.

Index Terms— Elliptic curve, cryptography, Fermat’s Last Theorem.

Introduction

Elliptic curves and its properties have been studied in
mathematics as pure mathematical concepts for long
since second or third century A.C. but its use in
cryptography is very recent. The name “elliptic” itself
was given in nineteenth century, though it has been
studied widely by many mathematicians. Use of
elliptic curve in cryptography was not known till 1984.
The first application in cryptography is found in
integer factorization method by Lenstra. In 1985, Victor
Miller and Neal Koblitz proposed completely different
cryptographic use of elliptic curves. Elliptic curve
cryptography (ECC) is public key cryptography. ECC is
based on properties of a particular type of equation
created from mathematical group. Equations based on
elliptic curves have characteristic that is very valuable
for cryptographic purpose. The main reason for
attractiveness of ECC is the fact that there is no sub
exponential algorithm known to solve the discrete
logarithm problem on a properly chosen elliptic curve.
This means that significantly smaller parameters can be
used in ECC with equivalent level of security.
Elliptic curves are the basis for a relative new class of
public key schemes. It is predicted that elliptic curves
will replace many existing schemes in near future. It is
fascinating to know the origin and development of
elliptic curves and how it has been used in
cryptography?
This paper throws light on historical background of
elliptic curves and its use in mathematics as well as
cryptography.

Prehistory of elliptic curves

Elliptic curve is a curve of the form y2 = p(x), where
p(x) is a cubic polynomial with no repeated roots.
Elliptic curve appears first time in the work of
Diophantus in second or third century A.D.
Diophantus had no concept of analytic geometry or
modern algebraic notations and certainly no idea about
elliptic curves. But for the first time where the elliptic curve appears is in the book of Diophantus’s “Arithmetica”. The problem written by him related to elliptic curve in his book read as follows:
“To divide a given number into two numbers such that their product is cube minus its side”. And the equation that Diophantus wrote is Y (a – Y) = X3 – X which is actually an elliptic curve in disguise. The way Diophantus solved the problem is as follows:
Consider the equation Y (a – Y) = X3 – X
Set a = 6 and Subtract 9 from both the sides gives
6Y – Y2 - 9 = X3 –X – 9
Replace Y by y+3 and X by –x gives y2 = x3 – x +9 which
is an elliptic curve.
Diophantus solved the problem for a = 6 by
substituting X = 3Y – 1, ignoring the double root he
obtained the solution y = 26/27 and x = 17/9. Therefore
the two numbers are y = 26/27 and a – y = 136/27 and
the product of these two numbers is (17/9)3 – (17/9).
The exact nature of what Diophantus accomplished in
the section of his problem took over 1500 years to
reveal itself completely.
Elliptic curves then occurs roughly in eighth century
and Fibonacci made it famous in eleventh century. He
encountered the problem as to find a rational number r
such that both r2 – 5 and
r2 + 5 are rational squares. Fibonacci found such
numbers namely, r = 41/6. Fibonacci called the positive
integer “n” a congruent number if r2 – n, r2, r2 + n are all
nonzero squares for some rational number r. The
connection with elliptic curve is that if n is a congruent
number then the product of the three nonzero rational
squares r2 – n, r2, r2 + n is also a rational square. If we
let r2 = x, we get the equation y2 = x(x-n)(x+n) , which
represents elliptic curve. Thus if n is a congruent
number, then the elliptic curve contains a nonzero
rational point.
French mathematician Bachet made a Latin translation

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 468

ISSN 2229-5518

of Diophantus’s Arithmetica and published it in 1621. Fermat acquired a copy of Arithmetica in 1630. Fermat’s collected works contains several references to problems involving elliptic curves. In particular, his conjecture that the only integers satisfying the equation y2 = x3 – 2 are (x, y) = (3, 5) or (3, -5) and that the only integers satisfying y2 = x3 – 4 are (x, y) = (2, 2), (2, -2), (5,
11), (5, -11).
Euler obtained the copy of Fermat’s work and he
expanded the scope of number theory far beyond

Fermat’s work, he gave number theory its status as a
legitimate field of mathematics. Euler also did quite a
bit of work on congruent number problem and derived
many results about elliptic integrals.
During 1670s Newton used recently developed tools of
analytic geometry to classify cubic curves. In doing so,
he explained the mysteries behind both Diophantus ‘
Arithmetica problem and Bachet’s theorem about
rational solution to elliptic curve.
In nineteenth century, Jacobi and Weirstrass connected
these efforts with elliptic integrals and elliptic
functions. In 1901, Poincare unified and generalized
this work to algebraic curve.
The name “elliptic” is given because of the fact that
these curves arose in studying the problem of finding
the arc length of an ellipse. If one writes down the
integral which gives the arc length of an ellipse and
makes elementary substitution, the integrand will
involve the square root of a cubic polynomial which is
named as elliptic curve.
The invention of integral calculus in 1660’s provided
the new tool for solving the question of finding arc
length of an ellipse. The first attempt to solve the arc
length of an ellipse involved series and not integrals. In
1669, Newton expressed the arc length of an ellipse as
an infinite series. Euler in 1733 and Maclaurin in 1742
also gave the series expression. To understand why, let
us investigate what actually the problem arises while
finding arc length of an ellipse.

Arc length of an ellipse

If y = f(x) is continuous and has continuous derivative

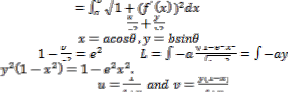
on the interval [a, b], then the arc length (L) of the
curve is given by L .
If the curve is an ellipse = 1 then with the
parametrization and the
substitution gives
where
Again the substitution gives rise
to an elliptic curve which is of the form

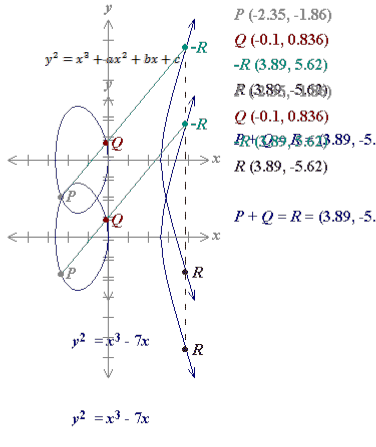
Group Law on elliptic curve

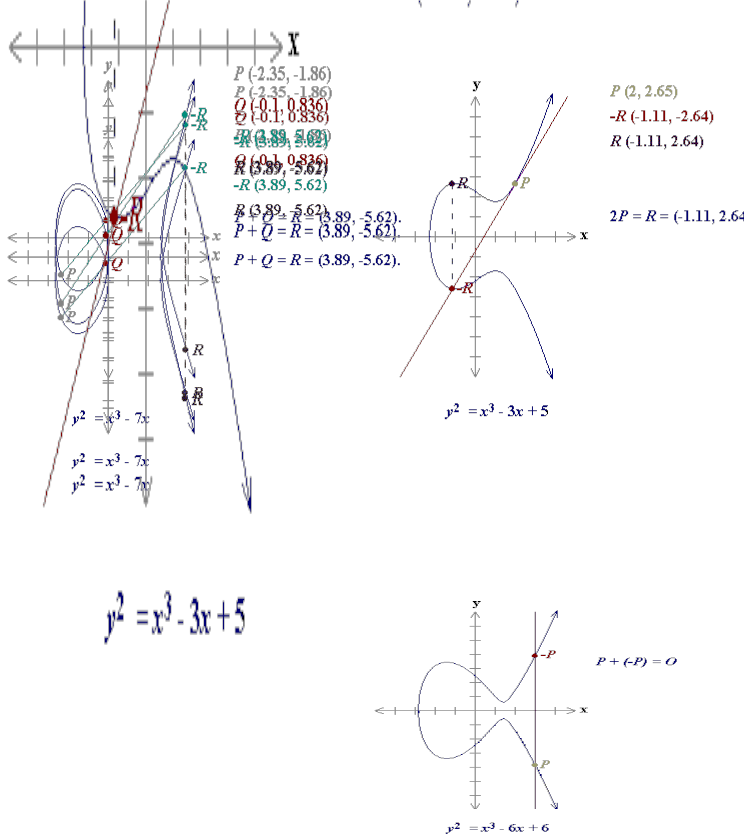
Let E : represents elliptic curve
over field IR. Let P, Q be the point on the elliptic curve.
Draw line through the points P and Q and find the
third intersection point “-R”. Draw the vertical line
through the point “-R”. Since the curve is symmetric
about x- axis we just take point R and reflect it above x-
axis. The corresponding point “R” represents addition
of two points P and Q. Set of all points on elliptic curve
along with the point at infinity, which is actually an
identity element form a group with binary operation
addition as defined above.

.

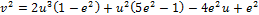
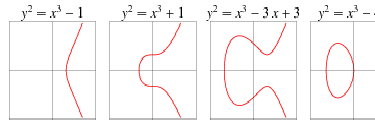
Definition of elliptic curve

An equation of the form 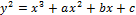is
called an elliptic curve. Some of the examples of elliptic
curves are as follows:

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 469

ISSN 2229-5518

Thus if P = (x1, y1 ) and Q = (x2, y2 ) then P + Q = R = (x3, y3 ) is given by
X3 = [(y2 - y1 )/(x2 - x1 )]2 – x1 - x2 .and y3 = -y1 + [(y2 - y1 )/(x2 - x1 )](x1 – x 3 )
If the points P and Q are same i.e. if the line through the point P meet the curve at point “-R” as shown in the figure below then in that case addition is taken as P+P = R.
If P = (x1, y1 ) and Q = (x2 , y2 ) and x1 = -x2 then P + Q = P
+ (-P) is defined to be an identity element, which is
point at infinity as shown below
.

Use of elliptic curves in cryptography

The first use of elliptic curves in cryptography was
Lenstra’s elliptic curve factoring algorithm. This
algorithm is a fast, sub exponential running time
algorithm for integer factorization which employs
elliptic curves. Lenstra invented new factorization

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 470

ISSN 2229-5518

method using elliptic curves and it set a process of finding cryptographic uses that had never before being studied for this purpose. The largest factor found using elliptic curve factorization method so far has 83 digits and was discovered on September 7, 2013 by R. Propper.
In 1985, N. Koblitz and V. Miller independently proposed using the group of points on an elliptic curve defined over a finite field in discrete log cryptosystem. It is completely different way of solving cryptographic problems. One can use elliptic curve group that is smaller in size while maintaining the same level of security. In many situations, the result is smaller key size, bandwidth savings and faster implementation, especially in smart cards and cell phones.
In 2005, the U. S. National Security agency posted a paper in which they recommended that, “take advantages of the past 30 years of public key research and analysis and move from first generation public key algorithm on to elliptic curves.

Public key cryptography

Public key cryptography is a “one-way” mathematical
process or function for which the inverse cannot
feasibly be computed. In RSA system, the process is to
take two very large randomly generated prime
numbers and multiply them together. The inverse
process is called integer factorization. In the Diffie-
Hellman system, the operation is exponentiation in a
finite field. The inverse of this process is called discrete
logarithm in finite field.

Discrete logarithm problem

Let E: 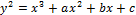represents elliptic curve
over finite field. Let P, Q be points on elliptic curve. The
problem is to find an integer k such that Q = KP.

Example

Let Consider an elliptic curve given by the equation y2
= x3 + 9x+ 17 (mod 23).
Let P = (4, 5) and Q = (16, 5), Elliptic curve discrete
logarithm problem is to find an integer k such that
kP = Q.
The integer k can be found by repeated point doubling
till we get Q.
Since P = (16, 5), 2P = (20, 20), 3P = (14, 14), 4P =(19, 20),
6P = (7, 3), 7P = (8, 7), 9P = (4, 5) = Q.
Thus 9P = Q and hence k = 9.

Solving discrete logarithm problem

At first the only algorithm known to solve the elliptic
curve discrete log problems were generic one, that is they have nothing to do with specific structures of elliptic curve group. The first such algorithm designed in the setting of finite field discrete log by Pohling and Hellman. He uses Chinese remainder theorem to reduce discrete log problem in the prime order subgroup. This is why the groups of prime orders are usually chosen fir Diffie-Hellman type cryptosystem.
In a group G of prime order n, the two best generic algorithms, Baby step – Giant step and Pollards rho algorithm each requires running time roughly 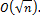Subsequently faster-than-square root algorithms were found for various classes of elliptic curves. However it still appears that the types of curves used in most cryptographic applications cannot be attacked by anything faster than the generic algorithms.

Conclusion

Jouney of elliptic curves since its inception is quite
fascinating and its use in cryptography is amazing.
After examining the security, implementation and
performance of ECC applications, we can conclude that
ECC is the most suitable public key cryptography
scheme for use. Its efficiency and security makes it an
attractive alternative to conventional cryptosystem. It is
without a doubt, fast being recognized as a powerful
cryptographic scheme.

References

[1] Neal Koblitz, A course in number theory and
cryptography, Springer – Verlag (2006)
[2] Neal Koblitz, Algebraic aspects of cryptographu,
Springer – verlag (1998)
[3] Joseph Silverman, John Tate, Rational Points On
Elliptic curves, Springer Velag (2010)
[4] Certicom, The elliptic curve cryptosystem: an
introduction to information security (2003)
[5] Adrian Rice, Ezra Brown, Why Ellipses are Not
Elliptic curves, Mathematical Magazine, vol.85, No.3,
June (2012) 163-176
[6] Amiee O’Malay, Elliptic curves and Elliptic curve
cryptography, B.S. Undergraduate Mathematics
Exchange, Vol.3, No. 1 (Fall 2005) 16-24.
[7] Ezra Brown, Bruce Myres, Elliptic curves from
Mordell to Diophantus and Back, The Mathematical
Association of America (Aug – sep 2002) 639-646.

International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014

ISSN 2229-5518

471

http /lwww .qs er .or g