International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 629

ISSN 2229-5518

Optimization of Tribological properties of Al-6082/SiC Metal Matrix Composite by Grey-Taguchi’s Method

Vijayanand Dharanikota

Abstract- Tribological behavior of aluminium alloy Al-6082 reinforced with silicon carbide particles (0%,5% & 10% Volume percentage of SiC) fabricated by powder metallurgy was investigated . In this paper the optimization of dry sliding performances on the aluminum hybrid metal matrix composite was done using grey relational analysis in the Taguchi method. Different loads, sliding speeds, sliding distances and varying percentage of Silicon Carbide are selected as control factors. The multiple responses to evaluate the dry sliding performances are specific wear rate and coefficient of friction. A series of L27 orthogonal array of experiments for three different samples of Al-6082 SiC MMCs have been conducted on pin-on-disc wear tester apparatus, the volume loss and frictional force are measured. Based on grey relational analysis, the optimum level parameters for specific wear rate and coefficient of friction have been identified. Analysis of Variance (ANOVA) had given the impact of individual factors on the specific wear rate as well as the coefficient of friction. The results indicated that the four test parameters had a significant role in controlling the friction and wear behavior of composites out of which %vol. was identified as most influential parameter followed by load for specific wear rate and load for coefficient of friction.

Index Terms— Aluminum hybrid metal matrix composite, Gray relation –taguchi’s Method, L27 orthogonal array , pin-on-disc wear tester

Dry sliding wear behavior, Analysis of variance.

——————————  ——————————

1 INTRODUCTION

oday our modern technologies require materials with unusual combinations of properties that cannot
be met by conventional ceramics, polymeric materials and metal alloys. This is true, especially for the material needed in transportation, aerospace and under water applications. These combinations of material properties are achieved by development of composites. These ma- terials fulfill the demand of almost all the engineering application due to their tremendous physical and me- chanical properties i.e. light weight, high strength, im- proved density and hardness, high wear and high corro- sion resistance.
Al and Al alloys became attractive candidate for the application in aerospace, defense and automotive industries owing to their versatile properties. A major requirement for such applications is the high strength along with reasonable ductility. There has been a con- stant effort to enhance the mechanical properties of Al alloys by alloying additions, heat treatment, thermo me- chanical processing, and severe plastic deformations and so on. The advantage of utilizing the beneficial properties of the constituent materials, to satisfy the specific demands, is the driving force for the develop- ment of composites. In this paper, our focus will be on the metal matrix composites (MMCs) and more especial- ly on the aluminium metal matrix composites.

Vijayanand Dharan ikota , graduated fro m NIT Warangal, And presen tly pursuing Mas ters in Industria l Engineer ing at Ar izona State Unive rsity, PH : +1-480-358-8930 ,

Email Id: vdharan1@asu.edu

Fabrication of MMCs has several challenges like porosity formation, poor wettability and improp- er distribution of reinforcement. The fabrication tech- niques of MMCs play a major role in the improve- ment of mechanical and tribological properties. The performance characteristics of Al alloy reinforced Achieving uniform distribution of reinforcement is the foremost important work.

The size and type of reinforcement also has a significant role in determining the mechanical and tribo- logical properties of the composites. The effect of type of reinforcements such as SiC whisker, alumina fiber and SiC particle fabricated by Powder Metallurgy on the properties of MMCs has been investigated. It was found that there existed a strong dependence on the kind of reinforcement and its volume fraction. The results re- vealed that particulate reinforcement is most beneficial for improving the wear resistance of MMC[1].
There is a growing interest worldwide in man- ufacturing hybrid metal matrix composites [HMMCs] which possesses combined properties of its reinforce- ments and exhibit improved physical, mechanical and tribological properties. Aluminium matrix composites reinforced silicon carbide was developed using powder metallurgy techniques. The reinforcements were varied by 0%,5% and 10% by volume. The composite was test- ed for dry sliding wear characteristics. The tribological properties of MMCs are also increased by increasing reinforcements at all applied conditions[2].

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 630

ISSN 2229-5518

2 DESIGN OF EXPERIMENTS

Design of Experiment is one of the important and pow- erful statistical techniques to study the effect of multiple variables simultaneously and involves a series of steps which must follow a certain sequence for the experiment to yield an improved understanding of process perfor- mance [3]. All designed experiments require a certain number of combinations of factors and levels be tested in order to observe the results of those test conditions. Taguchi approach relies on the assignment of factors in specific orthogonal arrays to determine those test com- binations. The DOE process is made up of three main phases: the planning phase, the conducting phase, and the analysis phase. A major step in the DOE process is the determination of the combination of factors and lev- els which will provide the desired information [4].
Analysis of the experimental results uses a signal to noise ratio to aid in the determination of the best pro- cess designs. This technique has been successfully used by researchers in the study of dry sliding wear behavior of composites. In the present work, a plan order for per- forming the experiments was generated by Taguchi method using orthogonal arrays [5]. Analysis of data from these designed experiments yields significance of influence of a factor or the interaction of factors on a particular output response and their % contribution.

3 GREY-RELATIONAL ANALYSIS

Grey relational analysis was proposed by Deng in 1989, is widely used for measuring the degree of relationship between sequences by grey relational grade. Grey rela- tional analysis is applied by several researchers to opti- mize control parameters having multi-responses through grey relational grade [6]. The use of Taguchi method with grey relational analysis to optimize the specific wear rate and co-efficient of friction with multi- ple process parameters.

A. Data Pre-Processing

In grey relational analysis, the data pre-processing is the first step performed to normalize the random grey data with different measurement units to transform them to dimensionless parameters. Thus, data pre-processing converts the original sequences to a set of comparable sequences. Different methods are employed to pre- process grey data depending upon the quality character- istics of the original data.
The original reference sequence and pre-
processed data (comparability sequence) are represent- ed by x0 (0)(k) and x i (0)(k) i =1,2,….,m; k =1,2,.....,n respec- tively, where m is the number of experiments and n is the total number of observations of data. Depending upon the quality characteristics, the three main catego- ries for normalizing the original sequence are identified
as follows: If the original sequence data has quality characteristic as ‘larger-the-better’ then the original data is preprocessed as ‘larger-the-best’:

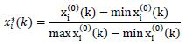(1)

If the original data has the quality characteristic as
‘smaller the better’, then original data is pre-processed as ‘smaller-the best’:

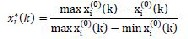(2) However, if the original data has a target optimum val-

ue (OV) then quality characteristic is ‘nominal-the-
better’ and the original data is pre-processed as ‘nomi-
nal-the-better’:

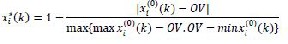
(3) Also, the original sequence is normalized by a simple

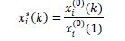
method in which all the values of the sequence are di- vided by the first value of the sequence.
(4)
where max xi(0)(k) and min xi (0)(k) are the maximum and
minimum values respectively of the original sequence xi(0)(k). Comparable sequence xi*(k) is the normalized sequence of original data.

B. Grey Relation Grade

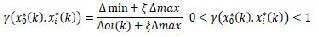
Next step is the calculation of deviation sequence, 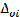(k) from the reference sequence of pre-processes data xi*(k) and the comparability sequence xi*(k). The grey rela- tional coefficient is calculated from the deviation se- quence using the following relation:

(5)

where (k) is the deviation sequence of the reference sequence x0 *(k) and comparability sequence xi*(k).

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 631

ISSN 2229-5518

𝜉 is the distinguishing coefficient 𝜉 ∈ [0,1]. The distin- guishing coefficient (𝜉) value is chosen to be 0.5. A grey
relational grade is the weighted average of the grey rela-

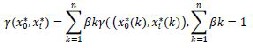
tional coefficient and is defined as follows:
(6)

The grey relational grade , represents the de- gree of correlation between the reference and compara- bility sequences. If two sequences are identical, then grey relational grade value equals unity. The grey rela- tional grade implies that the degree of influence related between the comparability sequence and the reference sequence. In case, if a particular comparability sequence has more influence on the reference sequence than the other ones, the grey relational grade for comparability and reference sequence will exceed that for the other grey relational grades. Hence, grey relational grade is an accurate measurement of the absolute difference in data between sequences and can be applied to appropriate the correlation between sequences.

4 MATERIAL SELECTION

4.1 Aluminium alloy Al6082:

In the present investigation, Al-6082 alloy was chosen as the base matrix as it has the excellent corrosion re- sistance and high strength in 6000 series alloys. In plate form, Aluminium alloy 6082 is the alloy most commonly used for machining. As a relatively new alloy, the higher strength of Aluminium alloy 6082 has seen it replace
6061 in many applications. The addition of a large amount of manganese controls the grain structure which in turn results in a stronger alloy. After the addition of SiC, due to the property of high hardness and high thermal conductivity, SiC accommodates in soft ductile aluminium base matrix, which enhance the wear resist- ing behavior of the Al – SiC metal matrix composite.
properties that are ideally suited for all electronic pack- aging applications requiring thermal management. The Al-SiC coefficient of thermal expansion (CTE) value is compatible with direct IC device attachment for the maximum thermal dissipation through the 170 – 200

W/mK thermal conductivity value material. Additional- ly, the low material density of AlSiC makes it ideal for weight sensitive applications such as portable devices.

Figure 1 Al-6082 SiC Microstructure

The ideal AlSiC material properties and the Al- SiC net-shape fabrication process provide low-cost high performance functional thermal management packaging solutions.

Table 2 Properties of Al-6082 SiC

Figure 2 Al-6082 Sic Samples of Different Compositions used for Wear test

Table 1 Chemical Composition of Al-6082 alloy

The above table gives us the chemical composi- tion of Al6082 the rest is aluminium.

4.2 Aluminium Silicon Carbide (Al-6082 Sic):

Aluminium Silicon Carbide (Al SiC) metal matrix com- posite (MMC) materials have a unique set of material

5 EXPERIMENTAL DETAILS

The aim of the experiment is to find the im- portant factors and combination of factors influenc- ing the wear process to achieve the minimum wear rate and coefficient of friction. The experiments were developed based on an orthogonal array, with the

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 632

ISSN 2229-5518

aim of relating the influence of sliding speed, applied load and sliding distance and Volume% . And the wear test is carried out using Pin-on-Disc wear device according to ASTM G99 standards. It consist of a rotary horizontal steel disc driven by variable speed motor A stationary test specimen with a defined normal force is pressed against the surface of another test specimen placed on the rotary disk.

During the test, the pin was held pressed against a rotating disc by applying load that acts as

counterweight and balances the pin. The load, sliding speed and sliding distance were varied in the range given in Table 3. A LVDT (load cell) on the lever arm helps determine the wear at any point of time by monitoring the movement of the arm. Once the sur- face in contact wears out, the load pushes the arm to remain in contact with the disc. This movement of the arm generates a signal which is used to determine the maximum wear and the coefficient of friction is moni- tored continuously as wear occurs and graphs be- tween co-efficient of friction and time was monitored for \ the specimens i.e.,0 %, 5% and 10% vol. SiC/ Al-6082 MMCs. Further, weight loss of each specimen was obtained by weighing the specimen before and after the experiment by a single pan electronic weigh- ing machine

Figure 3 Pin-On-Disc Friction and Wear tester

5 PLAN OF EXPERIMENTS

In full factorial design, the number of experimental runs exponentially increases with the increase in the number of factors as well as their levels. This results in huge ex- perimentation cost and considerable time period. So, in order to compromise these two adverse factors and to search for the optimal process condition through a lim- ited number of experimental runs Taguchi’s L27 orthog- onal array consisting of 27 runs was selected to optimize the tribological properties of Al-6082 Sic alloy. Experi- ments were conducted with the Factor levels as given in Table 3.

Table 3 Experimental Factors And Their Levels

Selected design matrix shown in Table 4 based on the Taguchi L27 orthogonal array consisting of 27 sets of coded conditions and the experimental results for the responses of specific wear rate (ws ) and coefficient of friction (µa ). All these data are used for the analysis and evaluation of the optimal parameters combination.
The specific wear rate and co-efficient of friction is calculated using following formulas:
Sliding Speed (m/s) = (2πN) /60
Sliding Distance (m) = πD * number of revolutions
Time (sec) = Sliding Speed / Sliding Distance
Wear Rate (g/s) = Weight loss / Time
Weight Loss = Initial Weight – Final Weight
Density (kg/mm3) = Mass / Volume
Specific Wear Rate (mm3/N-m) = V/ L*D Coefficient of friction = Ft / Fn
Where, N = Speed of disc in rpm
D = Wear track diameter in m

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 633

ISSN 2229-5518

18	-11.966	11.483	0.752	0.630	0.248	0.370
19	-22.793	13.979	0.346	0.795	0.654	0.205
20	-11.746	17.077	0.761	1	0.239	0
21	-15.038	14.894	0.637	0.856	0.363	0.144
22	-20.002	13.151	0.451	0.741	0.549	0.259
23	-9.866	14.894	0.831	0.856	0.169	0.144
24	-5.374	17.077	1	1	0	0
25	-12.289	14.894	0.740	0.856	0.260	0.144
26	-8.454	13.979	0.884	0.795	0.116	0.205
27	-10.252	13.979	0.817	0.795	0.183	0.205

Table 4 Orthogonal Array L 27 Of The Experimental

Runs & Results

The results for various combinations of parameters were obtained by conducting the experiment as per the Orthogonal array show in the Table 4. The meas- ured results were analyzed using the commercial software JMP specifically used for design of experi- ment applications.

6 ANALYSIS OF RESULTS

6.1 Grey relation analysis

The experimental results for specific wear rate (ws) , coefficient of friction (µa) are listed in the Table
4.Typically, smaller values of ws, µa are desirable. Thus the data sequences have the smaller-the-better characteristic, the “smaller-the-better” methodology, i.e. Equation (2).The normalized S/N ratio values were obtained based on the quality of characteristics.

Table 5 S/N ratio values, normalized S/N ratio values, and deviation sequences for Al-6082 SiC

The grey relational coefficients and grade values for each experiment are given in Table 6. Average grey rela- tional coefficient and grades for each level of a testing parameter calculated as per Taguchi method.

For both Specific wear rate and co- efficient of friction		For Specific wear rate		For co-efficient of friction
Exp. N.o	Grey Relation Grade	Rank	Exp. N.o	Grey Relation Coefficient	Rank	Exp. N.o	Grey Relation Coefficient	Rank
24	1	1	24		1	1	20	1	1
11	0.841	2	11		0.971	2	24	1	2
20	0.839	3	26		0.812	3	21	0.776	3
23	0.762	4	23		0.747	4	23	0.776	4
26	0.761	5	15		0.745	5	25	0.776	5
27	0.721	6	27		0.732	6	11	0.71	6
25	0.717	7	20		0.677	7	19	0.709	7
21	0.678	8	18		0.668	8	26	0.709	8
17	0.648	9	17		0.665	9	27	0.709	9
14	0.624	10	25		0.658	10	22	0.659	10
15	0.623	11	14		0.617	11	14	0.631	11
18	0.622	12	16		0.617	12	17	0.631	12
16	0.576	13	21		0.579	13	10	0.575	13
19	0.571	14	9		0.557	14	18	0.575	14
22	0.568	15	12		0.553	15	8	0.534	15
12	0.527	16	2		0.531	16	16	0.534	16
8	0.503	17	6		0.515	17	12	0.501	17
10	0.500	18	5		0.487	18	15	0.501	18
2	0.469	19	22		0.477	19	13	0.475	19
9	0.466	20	8		0.471	20	1	0.454	20
7	0.429	21	7		0.45	21	2	0.407	21
13	0.427	22	19		0.433	22	7	0.407	22
6	0.424	23	10		0.424	23	9	0.375	23
5	0.419	24	3		0.381	24	3	0.351	24
1	0.394	25	4		0.381	25	5	0.351	25
3	0.366	26	13		0.378	26	4	0.333	26
4	0.357	27	1		0.333	27	6	0.333	27

Table 6 The calculated grey relational coefficient and grey rela- tional grade Al-6082 SiC

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 634

ISSN 2229-5518

The following are the response tables for specific wear rate, coefficient of friction, and for both specific wear rate and coefficient of friction.

Graph 1 Effects of dry sliding parameter levels on specific wear rate of Al-6082 SiC

Table 7 Response Table for specific wear rate of Al-6082 SiC 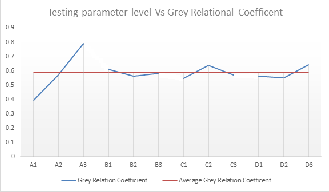Graph 2 Effects of dry sliding parameter levels on coefficient of

friction of Al-6082 SiC

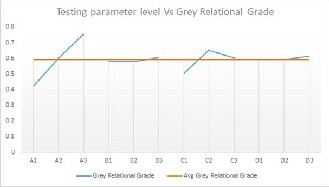
Table 8 Response Table for Coefficient of Friction Al-6082 SiC

Table 9 Response Table for both specific wear rate and coefficient of friction of Al-6082 SiC

The bold characters are shown to denote the opti- mum value of grey relational coefficient and grade in Tables 7, 8, 9. The effects of the testing parameter level versus the grey relational grade and grey relational coef- ficient values are given below for Al SiC MMCs.

Graph 3 Effects of dry sliding parameter levels for both specific wear rate and coefficient of friction of Al-6082 SiC

By using the grey relational coefficient values and grey relational grade values, the graphs are plotted for different parameter levels and grey relations. The optimum values are also drawn from the graphs.
The grey relation grades in Table 7-9 can be fur-

ther arranged in matrix form shown as follows:

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 635

ISSN 2229-5518

0.6794 0.6256 0.6642 0.6198
= 0.7904 0.6092 0.6388 0.6417
0.7561 0.6048 0.6518 0.6142

In grey relation analysis, the maximum analysis, the maximum value in each row represents the most influ- ential factors that affect the output variables. By compar- ing Row 1, Row 2, Row 3, Row 4, some conclusion from this matrix. In the first row, γ(W,A) > γ(W,C) > γ(W,B) > γ(W,D), it means that the order of importance for the controllable factor Specific wear rate (W), in sequence is the factor A,C,B,D. In the second row γ(Cf ,A) > γ(Cf ,D)

> γ(Cf ,C) > γ(Cf ,B), the order of importance for the con- trollable factors to Coefficient of friction (Cf) in the se- quence is the factor A,D,C,B. Similarly , based on the third row, γ(WCf ,A) > γ(WCf ,C) > γ(WCf ,D) > γ(WCf ,B) , The order of importance for the controllable factors to both specific Wear rate and Coefficient of friction (WCf), in the sequence is the factor A,C,D,B

6.2 Analysis Of Variance (ANOVA)

The experimental results were analyzed with Analysis of Variance (ANOVA) which is used to investigate the in- fluence of the considered wear parameters namely, slid- ing distance , applied load, sliding speed, and Sic vol- ume% that significantly affect the performance measures. By performing analysis of variance, it can be decided which independent factor dominates over the other and the percentage contribution of that particular independent variable. Table (6&7) SiC MMCs of the ANOVA results for wear rate and coefficient of friction for four factors varied at three levels and interactions of those factors. This analysis is carried out for a signifi- cance level of α=0.05, i.e. for a confidence level of 95%. Sources with a P-value less than 0.05 were considered to have a statistically significant contribution to the per- formance measures. After performing initial analysis on residuals it is found out that data need to be trans- formed to Stabilize the variance and interpret the results currently .
Specific Wear rate: = 1og( Co-efficient of friction: = 1/()

Table 10 Experimental Data after Transformation

Table 11 gives the results of analysis of variance (ANO- VA) for specific wear rate of Al-6082 Sic using JMP Soft- ware. According to table 11, the factor C i.e. Vol% of Sic with 25.73% of contribution is the most significant con- trolled parameters for dry sliding performance, followed by load with 21.25% contribution, and the last signifi- cant factor is interaction term between Load(A) and slid- ing distance(D) with 9.21% contribution for the minimi- zation of specific wear rate.

S. No

Load

(A)

Slid- ing Speed (B)

Vol% (C)

Slid- ing Dis- tance (D)

1ogS

1/µ a

9.81

1000

1.600

2.501

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 636

ISSN 2229-5518

ABD	1	1.064	1.064	2.019	0.181	1.4
ACD	1	0.046	0.046	0.088	0.772	0.1
BCD	1	0.233	0.233	0.442	0.519	0.3
Error	12	6.323	0.527			14.2
Total	26	78.06				100

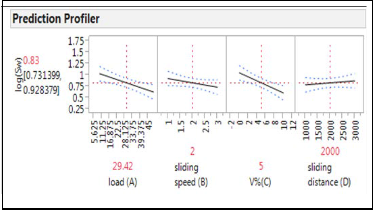
Table 11 ANOVA for specific wear rate

Graph 4 Main Factors v/s Specific Wear rate

Sw Load(A)

Sliding Distance(D)

Graph 5 Interaction between load & Sliding distance v/s Specific

Wear rate

From Table 11 A*D interaction is significant and from graphs 4 & 5 to obtain minimum specific Wear rate Load
,sliding speed, Vol% and sliding distance should main- tained at high level (i.e. 49.03N, 3m/s ,10%, 3000m re- spectively).

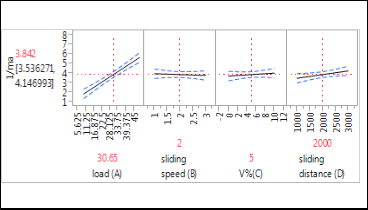
Table 12 ANOVA for Co-efficient of friction

Graph 6 Main Factors v/s Co-efficient of friction

Table 12 gives the results of analysis of variance (ANO- VA) for Co-efficient of Al-6082 Sic using JMP software. According to table 12, the factor A i.e. Load with 76.1% of contribution is the most significant controlled param- eters for dry sliding performance, for the minimization of Co-efficient of friction and no interaction terms are significant. And to obtain to obtain minimum Co- efficient of friction Load , Vol% and sliding distance should maintained at low level (i.e. 9.81N, , 0%, 1000m respectively) and sliding speed at high level (i.e. 3m/s) .

6.2.1 Multiple Linear Regression Model

A multiple linear regression model is developed using statistical software “JMP”. This model gives the relationship between an independent / predicted variable & a response variable by fitting a linear equation to observe data. Regression equation thus generated establishes correlation between the signifi- cant terms obtained from ANOVA analysis namely applied load, sliding speed, Vol% & sliding distance.

The reduced regression equation developed for Al-6082 SiC MMCs wear rate and coefficient of friction are as follows:

Sw = 1.37-0.012A-0.039C-0.000004(A-29.42)*(D-2000) -- Eq(7)

µa = 0.919+0.0953A ----- Eq(8)

From Eq (7), it is observed that the load, Vol%, Sliding distance increases, it will be decrease the wear rate But in case of coefficient of friction Eq (8), load

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 637

ISSN 2229-5518

plays a major role. Overall regression equation gives the clear indication about coefficient of friction is highly influenced by load.

7 CONCLUSION

Following are the conclusions drawn from the study on dry sliding wear test using Taguchi’s technique.

1) For the lowest specific wear rate, 49.03 N ap- plied load, 2 m/s sliding speed, 3000m sliding

distance and 10 Vol.% Silicon Carbide percent- age are used as optimal combination.

2) For the lowest coefficient of friction, 49.03 N applied load, 1 m/s sliding speed, 3000m sliding distance and 5 Vol.% Silicon Carbide percentage are used as optimal combination.

3) For both specific wear rate and coefficient of friction, the lowest values given are 49.03 N ap- plied load, 2 m/s sliding speed, 3000m sliding distance and 10 Vol.% Silicon Carbide percent- age.

4) Based on the ANOVA, Silicon Carbide volume percentage (25.73%) followed load (21.25%) , in-

teraction t between load and sliding distance (9.21%) exert a significant influence on specific wear rate of Aluminium composites.

5) Based on the ANOVA, load(76.1%) exert a sig-

nificant influence on coefficient of friction of
Aluminium composites.

6) The order of importance for controllable factors to the minimum specific wear rate, in sequence, is Vol% of Sic, load, sliding Speed and sliding distance; order to the coefficient of friction, in sequence is load, sliding distance, Vol.% of SiC sliding speed.

7) However, it is observed through ANOVA that the applied load is the most influential control

factor among the four dry sliding performance input parameters of Al SiC.

ACKNOWLEDGMENT

The wish to thank Prof. Dr. N. Selvaraj, Head, Depart- ment of Mechanical Engineering, Nat ional Ins tit ute of Technology, Warangal, Mr. Jeevan, PhD Scholar, NITW, and Prof. Rong Pan, Associate Professor, Arizona State Univer- sity .

REFERENCES

[1] Ashok Kr. Mishra, Rakesh Sheokand, Dr. R K Srivastava , Tribological Behaviour of Al-6061 / SiC Metal Matrix Compo- site by Taguchi’s Techniques, ijsrp Vol.2, Issue 10, ISSN 2250-

3153

[2] Manoj Singla, D. Deepak Dwivedi, Development of Alumini- um Based Silicon Carbide Particulate Metal Matrix Composite Journal of Minerals & Materials Characterization & Engineer- ing, Vol. 8, No.6, pp 455-467.

[3] G. Taguchi, introduction to quality engineering, Asian productivity organization, 1990

[4] R. A. Fisher, Design of Experiments, Oliver & Boyd, Edin- burgh, UK, 1951

[5] P. J. Ross, Taguchi Technique for Quality Engineering, McGraw Hill, New York, NY, USA, 2nd edition1996

[6] Sadasiva Rao T., Rajesh V., Venu Gopal A, Taguchi based Grey Relational Analysis to Optimize Face Milling Process with Multiple Performance Characteristics, ICTIME'2012, March 24-25, 2012 Dubai

[7] JMP User Manual 8 Design of Experiments Guide, Second

Edition Cary, NC: SAS Institute Inc.

[8] S. Dharmalingam, R. Subramanian, Optimization of Tribolog- ical Properties in Aluminum Hybrid Metal Matrix Composites Using Gray-Taguchi Method, JMEPEG (2011) 20:1457–1466.

[9] Hui-Hui Fu, Wear properties of Saffil/Al, Saffil/Al2O3/Al and Saffil/SiC/Al Hybrid metal matrix composites, Wear 256 (2004) 705–713.

[10] Design and Analysis of experiments , Douglas C.Montgomery, Wiley student 8th edition.

[11] N.Radhika,R.Subramanian, Tribological Behaviour of alumin-

ium / Alumina / Graphite Hybrid Metal Matrix Composite Using Taguchi‟s Techniques, Journal of Minerals & materials Characterization & Engineering, Vol. 10, No.5, pp.427-443,

2011.

[12] T. Sritharan, L.S. Chan , A feature of the reaction between Al and SiC particles in an MMC, Materials Characterization 47 (2001) 75– 77.

[13] P.K.Rohatgi, B.F.Schultz, Tribological performance of A206 aluminum alloy containing silica sand particles , Tribology In- ternational 43 (2010) 455–466.

[14] S. Basavarajappa, G. Chandramohan , Application of Taguchi

techniques to study dry sliding wear behaviour of metal ma- trix composites, Materials and Design 28 (2007) 1393–1398