some operating conditions. In the integral controller, if the
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2196
ISSN 2229-5518
Optimal Load Frequency Control in a Single Area
Power System Based Genetic Algorithm
Ahmed Jasim Sultan
—————————— ——————————
HE problem of controlling the real power output of gen- erating units in response to changes in system frequency and tie-line power inter-change within specified limits is
known as load frequency control (LFC) [1]. LFC is a very im- portant issue in power system operation and control for sup- plying sufficient and both good quality and reliable power. To
improve the stability of the power system, it is necessary to
two areas power system.
This paper presents real-valued genetic algorithm to tune the PID controller parameters. In order to guarantee the best results as well as to ensure the robustness of the proposed con- troller, different search criteria are implemented. This includes Integral of Time multiplied by Absolute Error (ITAE), Integral
of Absolute Magnitude of the Error (IAE), Integral of the
IJSER
design LFC systems that control the power generation and
active power [2]. Conventional LFC uses an integral controller.
The main drawback of this controller is that the dynamic per-
formance of the system is limited by its integral gain. A high
gain may deteriorate the system performance causing large
oscillations and instability [1]. Thus the integral gain must be
set to a level that provides a compromise between a desirable
transient recovery and low overshoot in the dynamic response of the overall system [3]. A lot of approaches have been re- ported in the literature to tune the gain of the fixed parameter PI controller [2, 4].
To overcome these drawbacks and to solve the load
frequency control problem effectively, neural network, Fuzzy
logic, and optimization algorithms as intelligent techniques are proposed by many authors [5-10].
Some control strategies have been suggested based on the conventional linear control theory; because of the complex-
Square of the Error (ISE), and Mean of the Square of the Error
(MSE).
Detailed
The frequency of a system is dependent on active pow-
er balance. As frequency is a common factor throughout the
system, a change in active power demand at one point is re-
flected throughout the system by a change in frequency. Be-
cause there are many generators supplying power into the
system, some means must be provided to allocate change in demand to the generators [1]. The block diagram of LFC of a single area power system is shown in Figure (1). It's obvious that the plant for LFC consist of three parts [1- 3]:
• 𝑮𝒈 (𝒔) is the governor with dynamics:
𝟏
ity of the power systems these controllers may be improper in
some operating conditions. In the integral controller, if the![]()
𝑮𝒈 (𝒔) =
𝑮
..………….. (1)
𝑺+𝟏
integral gain is very high, undesirable and unacceptable large
overshoots will be occurred. However, adjusting the maxi-
mum and minimum values of proportional (Kp), integral (Ki)
and integral (Kd) gains respectively, the outputs of the system
(voltage, frequency) could be improved.
• 𝑮𝒕 (𝒔) is the non-reheated turbine dynamics:
![]()
𝑮 𝒔) = 𝟏 ……………. (2)
𝑻𝑻 𝑺+𝟏
For reheated turbine:
(𝑭𝑯𝑷 𝑻𝑹𝑯 𝑺+𝟏)
In [11] the author proposed a load frequency control based Fuzzy, Particle swarm, and genetic algorithms for one![]()
𝑮𝒕 (𝒔) = (𝑻
𝑪𝑯
𝑺+𝟏)(𝑻
𝑹𝑯
𝑺+𝟏) ……………… (3)
and two area in power system. Comparison of performance responses of conventional PID controller with PID controller using different intelligent techniques for the both cases show that the fuzzy tuned controller has better satisfactory generali- zation capability, feasibility and reliability, as well as accuracy than GA and the PSO algorithms. Simulation results are car- ried out by 1 to 10% system disturbances in both of one and
• 𝑮𝒑 (𝒔) is the power system dynamics:
![]()
𝑮 𝒔) = 𝑲𝒑 ……………. (4)
𝑻𝒑 𝑺+𝟏
And ![]() is the droop characteristics.
is the droop characteristics.
Where:
∆𝑷𝑳 Load power disturbance (p.u. MW)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2197
ISSN 2229-5518
𝑲𝒑 Electric power system gain
𝑻𝒑 Electric power system time constant (s)
𝑻𝑻 Turbine time constant (s)
𝑻𝑮 Governor time constant (s)
𝑭𝑯𝑷 Fraction of total turbine power generated by High pres-
sure section.
𝑻𝑹𝑯 Reheater time constant
𝑻𝑪𝑯 Steam chest time constant
𝑹 Speed regulation due to governor action (Hz/p.u. MW)
ral selection. The basic goal of GA is to optimize functions called fitness functions. A possible solution to a specific prob- lem is seen as an individual. A collection of a number of indi- viduals is called a population. The current population repro- duces new individuals that are called the new generation. The new individuals of the new generation are supposed to have better performance than the individuals of the previous gen- eration [14]. GA have been successfully implemented in the area of industrial electronics, for instance, parameter and sys- tem identification, control robotics, pattern recognition, plan- ning and scheduling and classifier system [14-16].
The structure of the control system with RGA-PID controller is shown in Figure (2). It consists of a conventional PID control- ler with auto-tuning its gain coefficients based on GA and a control plant [17].
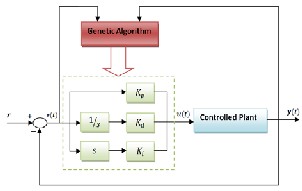
Fig. 1.Block Diagram of LFC LoIop for SJingle Area poweSr system ER
The power system can be described by the state-space equa- tion as following [4, 13]:
𝑿 = 𝑨𝑿 + 𝑩𝑩 + 𝚪𝒑 ……………… (5) Where A state matrix, B and 𝚪 are input and disturbance ma- trices, U and 𝒑 are input and disturbance vectors, and 𝑿 is

the state vector, given as:
..……………. (6)
……...……….. (7)
……………….. (8)
……………….. (9) Also
∆𝒇 Incremental frequency change.
∆𝑷𝑮 Incremental change in generator output (p.u. MW).
∆𝑿𝑬 Incremental change in governor valve position.
Fig. 2.Structure of RGA-PID controller
An auto-tuning RGA-PID controller can be implemented as fol- lows:
A. Encoding:
A real (floating point) numbers will be used to encode the
population. In this paper it is aimed to apply RGA to op-
timize the gains of a PID controller, hence three strings
will be assigned to each number of the population. The boundaries for the PID constants are chosen to ensure that not too many of the generated PID constants lead to an unstable system.
B. Initialization:
Initialize RGA by setting the number of individuals, the
number of generations, the crossover probability, and the mutation probability.
C. Fitness Function:
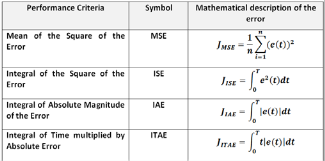
The fitness of an individual is calculated from four differ-
ent objective functions. To optimize the performance of a
PID controlled system, the PID gains of the system are ad- justed to maximize and minimize a certain performance index. The four performance indices can be shown in Ta- ble 1. The minimization fitness function becomes:
The genetic is a robust optimization technique based on natu-![]()
𝑭𝒊𝒕𝒏𝒆𝒔𝒔 𝑭𝒖𝒏𝒄𝒕𝒊𝒐𝒏 = 𝟏
𝑱
……………… (10)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2198
ISSN 2229-5518
TABLE 1
MATHEMATICAL DESCRIPTION FOR DIFFERENT SEARCH CRITERIA [12]
D. Selection:
The Normalized geometric selection is applied to select individuals in the current population pool.
E. Crossover:
Two parent chromosomes are crossed to produce one
child. Arithmetic crossover was chosen as the crossover
procedure.
F. Mutation:
Mutation changes the structure of the string by changing
each individual were set to lie between -100 to +100. The simula- tion results shown in Figures (4, 5, and 6) are carried out for four performance criteria such as; IAE, ISE, MSE, and ITAE. From Figure (4), the results of Non-reheated turbine can be concluded as illustrated in Table (2, 3). Table (2) demonstrates that settling time and peak overshoot of different control schemes uses by other researchers, Table (3) show that settling time and peak overshoot of for RGA-PID controllers using different perfor- mance criteria, It is seem that the ITAE has the shortest settling time and the lowest overshoot. The proposed controller has the best performance in damping of system oscillations compared to the other controllers.
TABLE 2
PERFORMANCE OF THE DIFFERENT TUNING ALGORITHM PID CONTROL-
LER FOR LFC OF NON-REHEATED TURBINE
the value of a bit chosen at random. The multi non- uniform mutation function was chosen as mutation opera- tor.
The object of the proposed auto-tuning RGA-PID controller is to search the optimal values of the gain coefficients Kp, Ki and Kd on-line in order to obtain a minimum fitness function value and to speed up the convergence of position tracking error and to improve the overall performance of controller. The block dia- gram of single area LFC system model controlled by the PID con- troller can be expressed by Figure (3).
Fig. 4.Frequency deviation step response of LFC for Non-Reheated turbine
Fig. 3.Single Area Power Generation Model [11]
ER-
In this section the proposed RGA-PID controller is applied to the system for LFC. In order to evaluate which of the previously mentioned four performance criteria produce the best results when used in conjunction with a real-valued genetic algorithm. The RGA was initialized with a population of 400 and was iterat- ed for 100 generations. The probability of crossover was set to
0.05 and probability of mutation was set to 0.4%. The bounds of
In case of 10% step increase in power demand shown in Figure (5). This Figure indicates the capability of proposed controller in damping oscillations. Moreover, the settling time of these oscilla- tions is approximately 1.09 second so the designed controller are capable of providing sufficient damping to the system oscillatory modes. From Figure (6), the results of Reheated turbine can be
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2199
ISSN 2229-5518
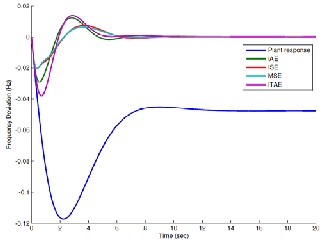
concluded as illustrated in Table (3). The Table (3) demonstrates that settling time and peak overshoot of the performance criteria ITAE has best response among other performance criteria.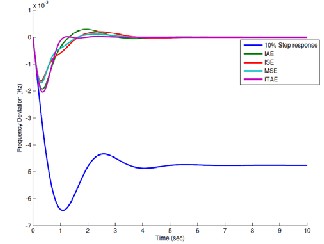
Fig. 4.Frequency deviation 10% step response of LFC for Non- Reheated turbine
been successfully suggested for the load frequency control problem. The proposed algorithm was applied to single area of power system with Non-reheated and Reheated turbines. From the simulation results obtained for load disturbances of RGA-PID controller with four performance indices IAE/ISE/MSE/ITAE that the RGA-PID controller with performance criteria ITAE is faster than the other in damping oscillations, Peak overshoot and Settling time were reduced.
[1] Kundur P. "Power system stability and control" McGraw-Hill, 1994. [2] Saadat H. "Power system analysis" McGraw-Hill, 1999.
[3] Elgerd, O. I., "Electric Energy System Theory: An Introduction" McGraw-Hill
Inc., 1971.
[4] Wen Tan "Tuning of PID load frequency controller for power system" Energy
Conversion and Management, Vol. 50, pp. 1465-1472, 2009.
[5] V. Shanmuga sundaram, Dr. T. Jayabarathi "Load Frequency Control using PID Tuned ANN Controller in Power System" 1st International Conference on Electrical Energy Systems (ICEES), 2011, India.
[6] Lokman H. Hassan, Haider A.F. Mohamed, M. Moghavvem, S.S. Yang "Load
Frequency Control of Power Systems with Sugeno Fuzzy Gain Scheduling
PID Controller" ICROS-SICE International Joint Conference, 2009, Japan.
[7] Wen Tan "Unified Tuning of PID Load Frequency Controller for Power Sys- tems via IMC" IEEE Transaction on power systems, Vol. 25, No. 1, Feb. 2010.
[8] MohammadSoroush Soheilirad, Mohammad Ali Jan Ghasab, Seyedmo-
hammahossein Sefidgar "Tuning of PID Controller for Multi Area Load Fre- quency Control by using Imperialist Competitive Algorithm" Journal of Basic and Applied Scientific Research, Vol. 2, No. 4, pp. 3461-3469, 2012.
![]()
[9] M. E-D. Mandour, E. S. Ali, M. E. Lottfy "Robust Load Frequency Controller
Design via Genetic Algorithm and H " Modern Electric Power Systems
2010, Wroclaw, Poland.
[10] E. Salim Ali, S. M. Abd-Elazim "Optimal PID Tuning for Load Frequency Control using Bacteria Foraging Optimization Algorithm" 14th International Middle East Power Systems Conference (MEPCON'10), Cairo University, Egypt, 2010.
[11] Mohamed M. Ismail, M. A. Mustafa Hassan "Load frequency Control Adap- tation using Artificial Intelligent Technique for one and two different areas
power system" International Journal of Control, Automation and Systems,
Fig. 4.Frequency deviation step response of LFC for Reheated tur-
bine
TABLE 1
PERFORMANCE OF THR RGA-PID CONTROLLER W ITH DIFFERNET PERFORMANCE CRITERIA OF LFC FOR REHEATED TURBINE

In this paper a PID controller which is tuned by the RGA has
Vol. 1, No. 1, Jan. 2012.
[12] Alwadie A. "Stabilization Load Frequency of a single area power system with Uncertain Parameters through a Genetically Tuned PID Controller" Interna- tional Journal of Engineering and Computer Science (IJECS-IJENS), Vol. 12, No. 6, 2012.
[13] D. Das," Electrical Power systems" New Age International Ltd., 2006.
[14] D. E. Goldberg, "Genetic Algorithms in Search, Optimization, and Machine
Learning", Addison-Wiley, 1989.
[15] Randy L. Haupt and Sue Ellen Haupt "Practical Genetic Algorithm" John
Wiley & Sons, 2004.
[16] K. F. Man, K.S. Tang, and S. Kwong, "Genetic algorithm: concepts and appli- cation" IEEE Trans. Industrial Electronics, Vol. 87, No. 9, 1996.
[17] Liu Fan and Er Meng Joo "Design for Auto-tuning PID Controller based on Genetic Algorithm" 4th IEEE conference on Industrial Electronics and applica- tions, China, 2009.
[18] B. Ogbonnaa, S.N. Ndubisib " Neural network based load frequency control for restructuring power industry" Nigerian Journal of Technology (NI-
JOTECH), Vol. 31, No. 1, pp. 40-47, 2012.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 2200
ISSN 2229-5518
![]()
The nominal values of the single area power system model pa- rameters are:
= 0.2 sec
= 0.3
= 7.0 sec
= 0.3 sec
= 0.05 (Hz/p.u. MW)
= 10 sec
= 1.0
IJSER
IJSER © 2014 http://www.ijser.org