
The design variables are the width of the reinforced concrete box culvert 1 , rise of the reinforced concrete box
temperature area steel in side walls x11 , all these variables
are shown in Fig. 1 below.
culvert
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1890
ISSN 2229-5518
Optimal Design of Reinforced Concrete Box
Culvert by Using Genetic Algorithms Method
Dr. Abdul-Hassan K. Al. Shukur1, Dr. Mohammed Abbas Al. Jumaili2, Hawraa Ali Hussein3
Abstract-This paper shows the optimal design of reinforced concrete box culvert based on minimum cost (economical design). The Genetic Algorithms (GAs) is the proposed method to optimize the structure which used as a tools box in MATLAB software version 2011, and the results of these method were verified by using Sequential Quadratic Programming (SQP) method which also used as tool box in
MATLAB software version 2011. The formulation of the problem includes 11 design variables: two geometrical, and 9 structural variables for the reinforcement set-up and the thickness of top, bottom, and the thickness of side walls. A parametric study was conducted to specify initial population and population size and concluded that the optimum results were obtain for initial population= [1.8 1.8 0.2 0.0001 0.0001
0.0001 0.0001 0.0001 0.0001 0.000232773728 0.000232773728], and population size=100.
Index Terms – Box Culvert, Genetic Algorithms MATLAB, Optimal Design, Population.
—————————— ——————————
steel required to resist positive moment in top slab (lower
The present design of economical concrete structures
x
layer) 5 , area steel required to resist negative moment in
mainly follows rules based on the experience of structural engineers. Most procedures adopt the cross-section
side wall (outer layer)
x6 , area steel required to resist
dimensions and material grades sanctioned by common
positive moment in side wall (inside layer)
x7 , area steel
practice. Once the structure is defined according to
experience, it is necessary to analyze the stress resultants
required to resist negative moment in bottom slab (outside
and compute the positive and negative reinforcement so as
layer)
x8 , area steel required to resist positive moment in
to satisfy the limit states prescribed by concrete codes. If the initial design dimensions or material grades be insufficient
bottom slab (inside layer)
x9 ,shrinkage and temperature
or excessive, the structure is redefined on a trial-and-error basis. Such a process leads to safe designs, but the cost of
area steel in top and bottom slabs
x10 , and shrinkage and
the concrete structures is highly dependent on the experience of the structural engineer. Moreover, these designs lack objectivity in the sense that different designers obtain different results despite adhering to the same concrete codes. Structural optimization methods are clear alternatives to designs based on experience [1].

The design variables are the width of the reinforced concrete box culvert 1 , rise of the reinforced concrete box
temperature area steel in side walls x11 , all these variables
are shown in Fig. 1 below.
culvert
x2 , thickness of top and bottom slabs and the
thickness of the side walls
x3 , area steel required to resist
negative moment in top slab (upper layer) x4 , area
————————————————

1(Professor of Civil Engineering, Engineering College/Babylon University, Babylon, Iraq)
2(Assistant Professor of Transportation Engineering, Engineering College/ Kufa University, Najaf, Iraq)
3(B.Sc. of Civil Engineering, Engineering College/ Kufa University, Najaf, Iraq)
Fig. 1. Typical section of reinforced concrete box culvert
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1891
ISSN 2229-5518
The problem of structural concrete optimization proposed in this study consists of an economic optimization. It deals
g 2 = 1 + K E +
2 gn 2 L
![]()
4 / 3
Q 2
![]()
gx 2 x
− H ≤ 0
2
with the minimization of the objective function
f ( X ) of
1 2
2 1 2
x x
expression below, satisfying as well the constraints of
section 2.3.
2(x1 + x2 )
f ( X ) = ( x1 + 2 x3 ) ( x2 + 2 x3 + D f )U ex + (( x1 + 2 x3 ) ( x2 + 2 x3 )2−.3.x11.3x2 )DUescign velocity at the peak design discharge rate determined from the hydrological analysis in
+ ( x1 + 2 x3 ) D f xU f
+ ( x1 + 2 x3 ) x4 ρ sU s + ( x1 + 2 x3 ) x5 ρ sU s
the culvert shall be greater than 1meter/second
+ + + + + + + +
for sediment transport conveyance capacity [4]
2 x3 ) x9 ρ sU s + 4 x10 ρ s xU s + 4 x11 ρ s xU s
3 Q
U ex =unit cost of excavation, ( unit price / m )
g 3 = 1 −
![]()
≤ 0
x1 x2
Uc = unit cost of concrete (labor and material), (
unit price / m 3 )
U =unit cost of earth fill, ( unit price / m 3 )
f
2.3.1.4 When velocities exceed about 3 (m/s), abrasion due to bed movement through the culvert and erosion downstream of outlet can increase significantly [5].
U s =unit cost of steel reinforcement (labor and material), (
unit price / ton )
g 4 =
Q
![]()
x1 x2
− 3 ≤ 0
ρ = density of steel reinforcement, ( Ton / m 3 )
The cost function is the value of materials and all the entries required to evaluate the entire cost of the reinforced concrete box culvert per linear meter (formwork, excavation, fill, etc). The prices considered were provided by local contractors of road construction in October 2012.
The objective function constraints used in this study is applied to ensure that the reinforced concrete box culvert constructed with minimum cost will accomplished all the necessary requirements required to performed its function perfectly thus these constraints are:
2.3.1.5 Box culverts and frames with clear span to rise ratios that exceed 4 are not recommended [6].![]()
g 5 1 − 4 ≤ 0
2
2.3.1.6 Slab thickness shall be equal to the following equation for crack control criteria [7].
g 6 = 0.0102 (3.3x1 + 10) − x3 ≤ 0
2.3.1.7 The primary reinforcing steel required to resist negative moment in top slab (upper layer) can be calculated as:
2.3.1.1 Where inlet control exits, the head
g = =0.85 f c
' bd
−
− 4M r1
![]()
− x ≤
required at culvert inlet is computed from the
7 f 1
1 1.53 f ' bd 2 4 0
orifice equation [2].
y c
g1 =
2g C
Q 2
![]()
2 ( x x )
− 1.2x ≤ 0
2
M =negative moment in top slab of reinforced
1
concrete box culvert.
2.3.1.2 To evaluate the outlet control hydraulics the condition of full flow in the culvert barrel will be used. The energy equation must incorporate the
2.3.1.8 The primary reinforcing steel shall be adequate to develop a factored flexural resistance, Mr, at least equal to the lesser of 1.2 times the cracking moment, Mcr and 1.33 times the factored
losses due to entrance ( ho ), friction ( h f
), and can be written as [3]:
), exit ( hex
moment required by the applicable strength load combinations.
M r = min (1.2M cr , 1.33M u )
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1892
ISSN 2229-5518
if M r = 1.2M cr
![]()
2.3.2.2 The primary reinforcing steel required to resist negative moment in side wall (outer layer) shall satisfy the following constraints:
0.85 f
' b d
148 x 2
g 8 = c 1 −
1 − 3 − x4 ≤ 0
f y
765
![]()
f ' d 2
' 4M
c
g13
0.85 f bd
![]()
= 1 −
1 − r3
'
- x
2 6
Else if M r = 1.33M u
f y
1.53 f
c bd
0.85 f
' b d
![]()
5.32M
g 8 =
c 1 −
1 − r1
'
− x ≤ 0
2 4
M =negative moment in exterior side wall of
3
f y
1.53 f c bd
reinforced concrete box culvert.
2.3.1.9 The provision for maximum reinforcement according to the LRFD deign method for
reinforced concrete box culvert is deleted since
for M r = 1.2M cr
![]()
' 2
2005 [7], but for optimization technique the
g14
0.85 f b d
![]()
= c 1 − 1 −
148 x3
− x6 ≤ 0
maximum value of steel reinforcement must be
specified, therefore the maximum steel
reinforcement will be specified depending on the
f y
765
' 2
c
provision of [8].
for M r = 1.33M u
f ' d
0.85 f
' b d
![]()
5.32M
c t
c
r3
g 9 = x4 − 0.428 * 0.85β1
![]()
fy d
≤ 0
g14 =
f 1 −
y
1 −
1.53 f ' bd
2 − x6 ≤ 0
![]()
'
f ' d
g10
![]()
= 0.85 f c bd 1 −
f
1 − 4M r2
1.53 f ' c bd 2
− x ≤ 0
5
g15 = x6 − 0.428 * 0.85β1
c
![]()
fy d
t ≤ 0
2.3.2.1 The primary reinforcing steel required to resist positive moment in top slab (lower layer) shall satisfy the following constraints:
2.3.2.3 The primary reinforcing steel required to resist positive moment in side wall (inner layer) shall satisfy the following constraints:
g = =0.85 f c
' bd
1 −
1 − 4M r4
− x ≤ 0
M =positive moment in top slab of reinforced
2
concrete box culvert.
16
y
![]()
1.53 f ' c bd 2
for M r = 1.2M cr
![]()
' 2
M = positive moment in exterior side wall of
4
reinforced concrete box culvert
for M r = 1.2M cr
g11
0.85 f b d
![]()
= c 1 − 1 −
148 t
− x5 ≤ 0
f y
765
f ' d 2
![]()
'
c
g17 =
0.85 f c b d
![]()
1 − 1 −
y
148 t 2
'
− x7 ≤ 0
2
for M r = 1.33M u
765
f c d
g11
= =0.85 f c
' b d
1 −
1 − 5.32M r2
'
![]()
− x ≤ 0
2 5
for M r = 1.33M u
f y
1.53 f c bd
0.85 f
' b d
![]()
5.32M
g17
= c 1 −
1 − r4
'
− x ≤ 0
2 7
'
![]()
t
f y
1.53 f c bd
g12 = x5 − 0.428 * 0.85β1
fy d
≤ 0
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1893
ISSN 2229-5518
f ' d
![]()
' 5.32M
g18 = x7 − 0.428 * 0.85β1
c
![]()
fy d
t ≤ 0
g 23
0.85 f b d
![]()
= 1 −
1 − r6
'
− x ≤ 0
2 9
f y
1.53 f c bd
2.3.2.4 The primary reinforcing steel required to resist
'
![]()
t
negative moment in bottom slab (lower layer)
shall satisfy the following constraints:
g 24 = x9 − 0.428 * 0.85β1
fy d
≤ 0
0.85 f
' bd
![]()
4M r
2.3.2.6 For shrinkage and temperature reinforcement in
g19 =
c 1 −
1 − 5
'
− x
2 8
top and bottom slabs the following constraints
f y
1.53 f
c bd
must be satisfied:
M =negative moment in bottom slab of
5
g 1.30 b x3 0
reinforced concrete box culvert.![]()
25 = 2 ( x
+ 3x3 ) f y
− x10 ≤
for M r = 1.2M cr
g 26 = 0.11 − x10 ≤ 0
![]()
' 2
g 27 = x10 − 0.6
g 20
0.85 f b d
![]()
= c 1 − 1 −
148 t
− x8 ≤ 0
f y
765
' 2
c
2.3.2.7 The constraints for shrinkage and temperature reinforcement in side walls can be stated by using
for M r = 1.33M u
the following equations:
1.30 b x3
g 20
= =0.85 f c
' b d
1 −
1 − 5.32M r2
'
![]()
− x ≤ 0
2 8
g 28
![]()
=
2 ( x2
+ 3x3 ) f y
− x11 ≤ 0
f y
1.53 f c bd
g29 = 0.11 − x11 ≤ 0
'
![]()
t
g 21 = x8 − 0.428 * 0.85β1
fy d
≤ 0
g 30 = x11 − 0.6
2.3.2.8 The shear resistance in top and bottom slabs
2.3.2.5 primary reinforcing steel required to resist
positive moment in bottom slab (lower layer) can
must satisfy the following constraints for
2.0 ft or more of fill:
g = =0.85 f c
' bd
1 −
1 − 4M r6
− x ≤ 0
g 28
= Vud
(top slab)
− φ 0.0676
![]()
f ' bd
e ≤ 0
22 f
![]()
1.53 f ' bd 2 9
y c
be calculated as:
g 29
= Vud
(bottom slab)
− φ 0.0676
![]()
f ' bd
e ≤ 0
M r
6 =negative moment in bottom lab of
reinforced concrete box culvert.
2.3.2.9 The shear resistance of concrete in side walls shall satisfy the following constraint for 2.0 ft or more of fill:
for M r = 1.2M cr
g 30 = Vud ( side wall ) − 0.0316β
![]()
f ' b d ≤ 0
![]()
' 2
2.3.2.10 For box culverts with less than 2.0 feet of fill.
g 23
0.85 f b d
![]()
= c 1 − 1 −
148 t
− x9 ≤ 0
The shear resistance of the concrete, Vc, for slabs
f y
765
' 2
c
and walls of box culverts shall satisfy the following
constraints:
for M r = 1.33M u
g 28 = Vud (top slab) −
0.0316β
![]()
f ' b d ≤ 0
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1894
ISSN 2229-5518
g 29
= Vud
(bottom slab)
− 0.0316β
![]()
f ' b d ≤ 0
2.3.3.5 the minimum thickness of reinforced concrete box culvert should be more than 8” (0.2m)
g 36 = 0.2 − x3 ≤ 0
g 30
= Vud
( side wall )
− 0.0316β
![]()
f ' b d ≤ 0
2.3.3.6 the following side constraints are specified for
2.3.3.1 The gross allowable load-bearing capacity of shallow foundations requires the application of a factor of safety (FS) to the gross ultimate bearing capacity [9] or
q all = u
Fs
qu ≥ q all Fs
better performance of the optimization technique
g 37 = x2 − 4 ≤ 0
g 38 = x2 − x1 ≤ 0
g 39 = x3 − 0.6 ≤ 0
An algorithm is a series of steps for solving a problem. A GA is a problem solving method that uses
q all = γ f
D f + γ c (( x1 + 2 x3 ) ( x 2 + 2 x3 ) − x1 x 2 ) / ( x1 + 2 x3 ) + γ w x 2
genetics as its model of problem solving. It’s a search technique to find approximate solutions to optimization
' 1 and search problems. The basic steps of GAs process are
![]()
qu = c N c Fcs Fcd + qN q Fqs Fqd + 2 γ s BN γ Fγs Fγd
[14]:
g 31 = (γ f
D f + γ c (( x1 + 2 x3 ) ( x2 + 2 x3 ) − x1 x2 ) /( x1 + 2 x3 ) + γ w x2 )Fs r-a(ncd' N c Fcs Focd +lation of n chromosomes (suitable solutions
om p pu
γ f ( x2
+ 2 x 3 + D f
) N q
Fqs
Fqd
![]()
+ 1 γ
2
s ( x1
+ 2 x3
) N γ
Fγs
Fγd ≤ 0
for the problem).
Step(2): Fitness Evaluation: Evaluate the fitness f(x) of each chromosome x in the population.
2.3.3.2 More than 70% of the soil type in Al –Najaf
city is sand soil in both the old and the new extension of Al-Najaf city with angle of internal friction ranging from (30 – 35) in old city and from (35 – 40) in the new extension of the city [10]. Therefore the total settlement will be equal to the elastic settlement only when the reinforced concrete box culvert is proposed to be constructed in Al- Najaf city.
Step(3): (Breeding): Create a new population by repeating following steps until the new population is complete.
crosso−ver 2was performed, offspring is the exact copy of
g = 1.86 (D γ
+ γ ((x
+ 2 x
) (x
+ 2 x
) − x x
)/ (x
+ 2 x
)) (x
+ 2 x
) 1
μ s I I ≤ 0
32 f f c 1 3 2
3 1 2 1
![]()
3 1 p3arents.
s
s f
2.3.3.3 Minimum box dimension shall be 0.9 by 0.9 m
[11].
g 33 = 0.9 − x1 ≤ 0
g 34 = 0.9 − x 2 ≤ 0
2.3.3.4 Four sided boxes can typically be used for spans up to 12 ft (3.5 m) [12].
g 35 = x1 − 3.5 ≤ 0
Step(4): Condition Criteria: If the end condition is satisfied, stop, and return the best solution in current population.
Step(5): Cycling Operation (Loop) Go to step (2)
for fitness evaluation.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1895
ISSN 2229-5518
4. APPLICATION AND VERIFICATION
In order to show the application of optimization solution using the objective function, constraints, and input data of material properties using genetic algorithm solver with MATLAB software the following example will be used as: Design the reinforced concrete box culvert to pass the
3
TABLE 2 RESULTS OF DESIGN EXAMPLE
design discharge of value equal to
(12 m
/ sec)
with
Headwall parallel to embankment (no wingwalls) (Square- edged on 3 edges) with coefficient of entrance loss
coefficient equal to ( K E
= 0.5 ) and total losses in culvert
barrel equal to (H=0.15), The length of box culvert equals to
(L=26.75 m).The depth of fill above the top slab of culvert
D f
equals to (
= 1m
), the properties of materials (concrete,
steel, foundation soil, and fill soil) and the price of material can be shown in Table 1.
TABLE 1 THE DATA OF DESIGN EXAMPLE
The solution of the example stated above (in
Application and verification) was found as shown in Table
2:
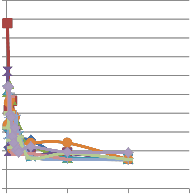
In this work, a detailed study of optimum design of reinforced concrete box culvert was carried out without initial population. Ten randomly runs using MATLAB software for each population size was utilized to study the effects of begin with randomly initial population and different population size. Results of these ten runs for each population size are showed in Table 3. Comparing these results with optimum design solution as shown in Table 2 indicates that the number of correct results is only one out of ten runs for each population size. The number of correct results is the counter of runs in which the correct value of objective function (fval=764.57) is obtained. Also as the population size is increased there is no noticeable improvement in the number of correct results and the elapse time of each run increases especially for population size more than 100. The comparison of optimum values for constant population size (i.e. Pop. size=100) can be shown in Fig. 2. It appears that the value of objective function of the first generation for each run is different due to randomly initial population. Therefore, it can be concluded that the case of GAs optimization without initial population is unsuitable to the problem under
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1896
ISSN 2229-5518
consideration and it seems necessary to specify the initial population (i.e. initial point).
TABLE 3: COMPARISON OF RESULTS FOR VARIOUS POPULATION SIZE WITHOUT INITIAL POPULATION
*Best Results
Comparing these results with optimum design
each run is different due to randomly initial population. Therefore, it can be concluded that the case of GAs optimization without initial population is unsuitable to the problem under consideration and it seems necessary to specify the initial population (i.e. initial point).
In this study, the method of specifying initial population is
adopted due to simplicity. To select initial population, a
parametric study was carried out using 100 as population size and different set of initial values were chosen within bound limits of design variables, the following initial population was chosen as initial population for each case study in this search [ 1.8 1.8 0.2 0.0001 0.0001 0.0001 0.0001
0.0001 0.0001 0.000232773728 0.000232773728].
5000
4500
4000
3500
3000
2500
2000
1500
1000
500
0
![]()
0 50 100 150
![]()
Generation
![]()
Run no.1
![]()
Run no.2
![]()
Run no.3
![]()
Run no.4
![]()
Run no.5
![]()
Run no.6
![]()
Run no.7
![]()
Run no.8
Run no.9
Run no.10
Figure 1: comparison of results with constant population size (Pop size
=100) of design example (without initial population)
solution as shown in Table 2 indicates that the number of correct results is only one out of ten runs for each population size. The number of correct results is the counter of runs in which the correct value of objective function (fval=764.57) is obtained. Also as the population size is increased there is no noticeable improvement in the number of correct results and the elapse time of each run increases especially for population size more than 100. The comparison of optimum values for constant population size (i.e. Pop. size=100) can be shown in Fig. 2. It appears that the value of objective function of the first generation for
To investigate the effects of initial population, population
size, and establish the suitable population size, ten randomly runs were carried out for the example in the application process with initial population for each population size. Optimum values of these runs are showed in Table 4.
The comparison of the results of Tables 3 and 4 with and without initial population respectively indicates the effects of the initial population. In the case of solution without initial population and 1000 population size only one runs out of ten runs the correct result is obtained. While all in ten runs, the correct result is reached in the case of solution with initial population and only 100 population size. Also, it appears that as the population size is increased the number of correct result is increased. It seems that the optimum design solution of deign example can be achieved with initial population and 100 population size or more.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1897
ISSN 2229-5518
TABLE 4 COMPARISON OF 10 RANDOMLY RUNS WITH BASIC INITIAL POINT FOR VARIOUS POPULATION SIZE
Pop .size | Objective function (Total Price) UP | |||||||||
Pop .size | un | un | un | un | un | un | un | un no8 | un no9 | un |
10 | 847.8 | 956.9 | 830.1 | 886.5 | 865.3 | 874.0 | 954.0 | 837.9 | 953.87 | 870.87 |
20 | 848.4 | 819.2 | 834.0 | 820.1 | 800.1 | 807.4 | 834.2 | 813.6 | 809.79 | 827.59 |
30 | 780.9 | 848.5 | 831.9 | 809.6 | 837.1 | 764.5 | 817.5 | 816.8 | 835.81 | 796.91 |
40 | 764.5 | 806,8 | 787,2 | 891,2 | 776,9 | 795,3 | 774,7 | 790,0 | 768,69 | 764.55 |
50 | 764.5 | 776.9 | 764.5 | 780,2 | 764.5 | 780.4 | 777.2 | 764.5 | 726.57 | 810.85 |
60 | 764.5 | 779,9 | 800,4 | 780,8 | 783,7 | 764.5 | 797,0 | 764.5 | 764.55 | 827,76 |
70 | 764.5 | 764.5 | 787.0 | 809.6 | 771.9 | 764.5 | 776,9 | 764.5 | 764.57 | 777.13 |
80 | 783.2 | 777.2 | 764.5 | 764.5 | 787,3 | 764.5 | 764.5 | 775.0 | 771.32 | 764.57 |
90 | 764.5 | 764.5 | 764.5 | 776.5 | 764.5 | 764.5 | 779.7 | 764.5 | 764.56 | 776.42 |
100 | 764.5 | 764.5 | 764.5 | 764.5 | 764.5 | 764.5 | 764.5 | 764.5 | 764.57 | 764.56 |
This is another optimization method. Sequential Quadratic Programming (SQP) method of gradient approach is used to verify the result of GAs optimization method using the same objective and constraints functions, input data of material properties, and same initial point, the final results coincide with the optimum solution using GAs optimization method as shown in Table 5.
TABLE 5: VERIFICATION OF RESULTS USING TWO OPTIMIZATION METHODS
It is found that the genetic algorithms GAs optimization method is a suitable method that can be used to obtain the minimum cost (i.e. optimum design) of reinforced concrete box culvert.
It is important for any optimization problem using genetic optimization method to carry out the convergence studies to investigate the capability of establishing the optimum design with or without initial population and governing population size.
It can be noted for this study that the initial population of
[1.8 1.8 0.2 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0.000232773728 0.000232773728] (i.e. initial point) and population size of 100 give the correct results. While without initial population, there is no convergence even with high population size of 1000.
[1] Yepes, V., Alcala, J., Perea, C., Vidosa, F., G., (2007), “A parametric study of optimum earth-retaining walls by simulated annealing” www.sciencedirect.com .
[2] United States Department of The Interior Bureau of Replacement, (1987), “Design of Small Canal Structures”, United States Government Printing Office, Denver.
[3] Tuncok, I., K., Mays, L., W., (2004), “Hydraulic Design
of Culverts and Highway Structures” Chapter 15:
[4] United States Army Corps of Engineers, (2009), “AED Design Requirements”: Culverts & Causeways.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1898
ISSN 2229-5518
[5] Washington State Department of Transportation, (2006), “Hydraulics Manual”.
[6] Reinforced concrete box culverts and similar structures, (2005), “Highway Design Manual”, Revision 47.
[7] American Association of State Highway and Transportation Official, (2010), “ AASHTO LRFD Bridge Design Specifications”. Washington, D.C.
[8] American Concrete Institute, (2011), “Building Code
Requirements for Structural Concrete (ACI 318M-11)”.
[9] Das, B., M., (2011), “ Principle of Foundation
7 th
Engineering”,
America.
Edition, Printed in the United States of
[10] Al Shakerchy, M., S., (2000), “Geotechnical Properties of Al Najaf City Soil with Emphasis on Infiltration and Strength Characteristics”. Ph. D Thesis, University of Technology, Building and Construction Engineering Department.
[11] Storm Water Management Design Manual, (2006), Culverts and Bridges, Georgetown County, South Carolina. [12] The State of Delaware Department of Transportation, (2005), “ Bridge Deign Manual”, Chapter seven: Culvert, Rigid Frame and Arch design.
[13] Sivanandam, S. N., and Deepa, S. N., (2008), “Introduction to Genetic Algorithm”, Springer, New York, USA.
[14] MATLAB, version 2011, “Optimization Toolbox -
User’s Guide”.
IJSER © 2014 http://www.ijser.org