International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 688

ISSN 2229-5518

Moment of Inertia for a Baseball or Softball Bat

Madhubala Pahade1, Vandana Jha2

Email: pahademadhu@yahoo.com, vandana_stpl@rediffmail.com

Abstract—In selecting a baseball or a softball bat, both weight and weight distribution should be considered. However, these considerations must be individualized, because there is large variability in how different batters swing a bat and in how each batter swings different bats. Previous research has defined the ideal bat weight as that weight that maximizes the batted-ball speed based on measurements of individual swings, the concept of the coefficient of restitution, and the laws of conservation of momentum. In this paper, a method is given that extends this approach to recent bat designs where the moment of inertia can be specified. The data presented in this paper show that all of the players in our study would probably profit from using end-loaded bats.

Keywords: Baseball, bat design, biological system modeling, coefficient of restitution, end-loaded, ideal bat weight, moment of inertia, science of baseball, softball, sweet spot.

——————————  ——————————

1. INTRODUCTION

TED Williams said that hitting a baseball is the hardest act in all of sports [20]. This act is easier if the right bat is used, but it is difficult to determine the right bat for each individual. Therefore, we developed the Bat Chooser 1 to measure the swings of an individual, make a model for that person, and compute his or her Ideal Bat Weight 1 [4], [5]. The Bat Chooser uses individual swing speeds, coefficient of restitution data, and the laws of conservation of momentum, and then it computes the ideal bat weight for each individual, trading off maximum batted-ball speed with accuracy. However, with the advent of lightweight aluminum bats, it is now possible for bat manufacturers to vary not only the weight but also the weight distribution.

They can start with a lightweight aluminum shell and add a weight inside the barrel to bring the bat up to its specified weight. This internal weight can be placed anywhere inside the barrel. When the weight is placed at the tip of the bat, the bat is said to be end loaded. So now, there is a need to determine the best weight distribution in general for certain classes of players and for individual players. That is the topic of this paper.

2. METHODS AND MATERIALS

A. Moment of Inertia
To compute the moments of inertia of our bats, we
drilled a hole in the knob and put a low-friction fishing line through 1Bat Chooser and Ideal Bat Weight are trademarks of Bahill.
Then, we swung each bat like a pendulum (through small angles) and measured its period of oscillation. We also measured the mass of the bat
and the distance from the hole in the knob to the center of mass . Each bat’s moment of inertia with respect to the hole in the knob was calculated with the following equation from [16]:
(1)
where the period is in seconds, the bat mass is in
kilograms, is in meters, and the gravitational constant at the University of Arizona is m/s. Because different experimenters use different reference points for the moment of inertia, we would like to be able to translate between them. The parallel axis theorem can be used to compute the moment of inertia about the center of mass.
(2)
We used two sets of bats in our variable moment of
inertia experiments. They are described in Tables I and II. We tried to make the bats in each set as similar as possible, except for the moment of inertia.
The bats of Table I look like normal bats. They had
similar lengths and masses. We started with Easton Model SE910 aluminum bats and added internal weights at different points so that they have different moments of inertia. However, the range of moments of inertia for these bats is small compared with bats in common usage today.
To get a larger range of moments of inertia, we made wooden bat handles and mounted 0.25-in,
40-cm-long threaded rods. Then, 0.269-kg brass
disks were fixed at various points on the rods. These bats are described in Table II. They have similar lengths and masses but a wide range for moments of inertia. Because of their wide range for the moments of inertia, this is the preferred set of bats for most of our experiments. Their moments of inertia span the range of commercially available bats, excluding Tee Ball and the professional major leagues, where the moments of inertia of the bats

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 689

ISSN 2229-5518

actually used are less variable. For comparison purposes, Table III shows the properties of several commercially available bats.
B. Coefficient of Restitution
The coefficient of restitution (CoR) is often defined as the ratio of the relative speed after a collision to the relative speed before the collision [14], [16], [18]. In our studies, the CoR is used to model the energy transferred to the ball in a collision with a bat. If the CoR were 1.0, then all the original energy would be recovered in the motion of the system after impact, but if there were losses due to energy dissipation or energy storage, then the CoR would be less than 1.0. For example, in a bat-ball collision, there is energy dissipation: both the bat and the ball increase slightly in temperature. In addition, both the bat and the ball store energy in vibrations. This energy is not available to be transferred to the ball and therefore the ball velocity is smaller. (We ignore the kinetic energy stored in the ball’s spin.) The CoR depends on many things, including the shape of the object that is colliding with the ball. When a baseball is shot out of an air cannon onto a flat wooden wall, most of the ball’s deformation is restricted to the outer layers: the cowhide cover and the four yarn shells. However, in a high-speed collision between a baseball and a cylindrical bat, we hypothesize that the deformation penetrates into the cushioned cork center. This would
allow more energy to be stored and released in the
ball, and the CoR would be higher. In our model, the CoR for a baseball-bat collision is 1.17 times the CoR of a baseball-wall collision. The CoR also depends on the speed of the collision. Our computer programs use the following equations for the CoR:
For an aluminum bat and a softball
Where Collision Speed (the sum of the magnitudes of the pitch speed and the bat speed) is in miles per hour. These equations come from unpublished data provided by J. Heald of Worth Sports Co., and they assume a collision at the sweet spot, which will be defined next. Our baseball CoR equation is in concordance with data from six studies summarized in an NCAA baseball report [9]: CoR Collision Speed .
The CoR also depends on where the ball hits the bat, because different locations produce different vibrations in the bat [1], [14], [15], [17]. Temperature also affects CoR [1], but we will not consider these complexities in this paper.
C. Sweet Spot of the Bat
For skilled batters, we assume that most bat-ball collisions occur near the sweet spot of the bat, which is, however, difficult to define precisely. The sweet spot has been defined as the center of percussion, the maximum energy transfer point, the maximum batted-ball speed point, the maximum coefficient of restitution point, the node of the fundamental vibration mode, the minimum sensation point, and the joy spot [3]. Let us now examine a few of these definitions.
1) When the ball hits the bat, it produces a translation that pushes the hands back and a rotation that pulls the hands forward. When a ball is hit at the center of percussion (CoP) for the pivot point, these two movements cancel out, and the batter feels no sting [6].
2) A collision at the maximum energy transfer point transfers the most energy to the ball [6].
3) There is a place on the bat that produces the maximum batted ball speed [7], [10].
4) The maximum coefficient of restitution point is the point that produces the maximum CoR for a bat-ball collision [14].
5) The node of the fundamental vibration mode is the point where the fundamental vibration mode of the bat has a null point [1], [11], [14], [17]. To find this node, with your fingers and thumb. Tap the barrel at various points with an impact hammer. The point where you feel no vibration and hear almost nothing (except the high frequency crack) is the node. A rubber mallet could be used in place of an impact hammer: The point is that the hammer itself should not produce any noise.
6) For most humans, the sense of touch is sensitive to vibrations between 100 and 500 Hz. For each person, there is a collision point on the bat that would minimize these sensations in the hands [2].
7) There is an area that minimizes the total (translation plus rotation plus vibration) energy in the handle. This area depends on the fundamental mode, the second mode, and the center of percussion [12].
8) Finally, TedWilliams [20] said that hitting the ball at the joy spot makes you the happiest. These eight points may be different, but they are close together. We group them together and refer to this region as the sweet spot. We measured a large number of bats and found that the sweet spot was about 80 to 85% of the distance from the knob to the end of the bat. This finding is in accord with [1],

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 690

ISSN 2229-5518

[2], [6], [11], [12], [14], [17], [20] as well as Worth Sports Co. (personal communication) and Easton Aluminum, Inc. (personal communication). Measuring from the other end of the bat, the distance from the barrel end of the bat to the sweet spot is about 13 to 18 cm (5 to 7 in) for typical adult-sized aluminum and wooden bats used in baseball and softball. It does not make sense to try getting greater precision in the definition of the sweet spot because the concept of a sweet spot is a human concept, and it probably changes from human to human. For example, in calculating the center of percussion, we would need to know the pivot point of the bat, and this may change from batter to batter.
D. Bat Chooser
Our instrument for measuring bat speeds has two vertical laser beams, each with an associated light detector. The subjects were positioned so that when they swung the bats the “sweet spot” (which we defined to be a point on the bat that is 29 in from the knob for adults and 26 in from the knob for children) of each bat passed through the laser beams. A computer recorded the time between interruptions of the laser beams. Knowing the distance between the laser beams (15 cm or 6 in) and the time required for the bat to travel that distance, the computer calculated the horizontal speed of the bat’s sweet spot for each swing. This is a simple model, because the motion of the bat is very complex, being comprised of a horizontal translation, a rotation about the batter’s spine, a rotation about a point between the two hands (which may be moving [13]), and a vertical motion. In our variable moment of inertia experiments, which will be described in Section III, and in our ideal bat weight experiments described in previous publications [3]–[5], [18], each player was positioned so that bat speed was measured at the point where the subject’s front foot hit the ground. We believe that this is the place where most players reach maximum bat speed [19]. The batters were told to swing each bat as fast as possible while still maintaining control. They were told to “Pretend you are trying to hit a Randy Johnson fastball.” In a 20-minute interval of time, each subject swung each bat through the instrument five times. The order of presentation was randomized. To reduce bat swing variability, we gave the batters a visual target to swing at. It was a knot on the end of a string hanging from the ceiling. Typically, this knot was 1.15 m off the floor. The height of this knot was important for some batters.

3. VARIABLE MOMENT OF INERTIA

EXPERIMENTS

Over the last dozen years, there has been a lot of between hitter variability in our variable moment of inertia experimental data. The resulting confusion caused us to stop doing those experiments. With retrospective analysis, we now know that most of the variability was due to subject life experiences. The Chinese students who had never played baseball fell into one group, the Americans who grew up playing baseball fell in to another group, and the women softball players fell into yet another group.

Fig. 1 shows the speed of the sweet spot of the bat as a function of the bat moment of inertia for 20 serious male batters who were active ball players and who had a lot of experience playing baseball and softball. Their ages ranged from 14 to 60 years. It is surprising to see upward slopes, but this is clearly a result of using moments of inertia in the normal bat range. No one could have a positive slope for very large moments of inertia. There is a lot of variability in these data, but it is not due to sex, country of origin, or the type of fit. These straight lines resulted from linear regression analysis of the average swing speeds of four bats. Over the last dozen years, we measured the bat speeds of players on the University of Arizona softball team. The lines of best fit for these batters are given in Fig. 2. They show less variation than those of Fig. 1. To provide a feel for these numbers, note that our simulation shows that it takes a sweet-spot bat speed of 22 m/s (50 mi/h), producing a batted-ball speed of 32 m/s (71 mi/h) to drive a perfectly hit softball over the leftfield fence (61 m or 200 ft) of Hillenbrand stadium at the University of Arizona. About half of these players are capable of doing this.
Fig. 1. Linear regression lines for the speed of the sweet spot of the bat as a function of the moment of inertia with respect to the knob I for various male batters.

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 691

ISSN 2229-5518

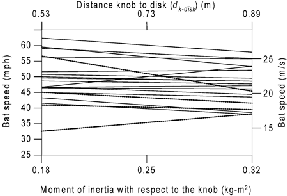
the disk (0.9 m) corresponds to a moment of inertia that is larger than that of the commercially available end-loaded bats listed in Table III. In fact,
0.9 m is beyond the end of the bat! Therefore, all of the batters of Fig. 2 would profit from using end loaded bats.
Fig. 2. Linear regression lines for the speed of the sweet spot of the bat as a function of the moment of inertia with respect to the knob for women on the University of Arizona softball team.

4. MODELS FOR THE VARIABLE MOMENT OF

INERTIA DATA

We model the swing of a bat as a translation and two
rotations: one centered in the batter’s body and the
other between the batters hands. Next, we compute the batted-ball speed (the speed of the ball after its collision with the bat). We use conservation of linear and angular momentum and the definition of the coefficient of restitution to get (4), shown at the bottom of the page, which has been previously derived [7], [18]. CoR is the coefficient of restitution of the bat-ball collision. is the distance between the center of mass and the sweet spot, which is assumed to be the point of collision; is the moment of inertia about the center of mass. The term is simply the velocity of the sweet spot, which is presented in Figs. 1 and 2. is a negative number, CoR CoR (4). The data for each player of Fig. 2 can be fit with a line of the
form slope intercept where slope is the slope of the line, and intercept is the –axis intercept. The bat is composed of a handle and a disk, so where is the inertia of the total bat with respect to the knob, is the inertia of the handle part of the bat with respect to the knob, is the mass of the disk on the end of the rod, and is the distance from the knob to the disk. Summing moments about the knob, we get which for now can be simplified as From (2), we have Assuming (as we have throughout this paper) that the sweet spot is 29 in (0.74 m) from the knob. Instead of hopeless analytical study, we will plot this function. Using a pitch speed of 60 mi/h, a softball, and the player of Fig. 2 with the biggest negative slope produces (8) and Fig. 3 slope intercept (8) Curves for the other batters of Fig. 2 had similar shapes, except for batters with positive slopes, where for above 1, the curves were asymptotically increasing. The smallest distance to
At this point, it may be useful to reiterate that an end-loaded bat is not a normal bat with a weight attached to its end. Adding a weight to the end of a normal bat would increase both the weight and the moment of inertia. This would not be likely to help anyone. In the design and manufacture of an end- loaded bat, the weight is distributed so that the bat has a normal weight but a larger than normal moment of inertia.

5. DISCUSSION

A. Bat Engineering
For the past decade, bat manufacturers have been
making end-loaded bats. They had no evidence that such bats would be advantageous. We have now provided that evidence. Furthermore, our data show that our subjects would profit from using bats that are even more end-loaded than those that are presently available.

The NCAA and other organizations regulate bats. Recently, they said that a baseball bat could not be more than 3 oz less than its length in inches. So, bat manufactures sought to add weight, but where should they add the weight? It had been suggested CoR) slope intercept (6) CoR slope intercept (7)
Fig. 3. Batted-ball speed as a function
The results of this paper suggest that they should add the weight to the end of the bat. This will comply with the regulation, decrease the bat speed slightly, but it will probably increase the batted-ball speed.
Recently, several baseball organizations have tried to limit bat performance by regulating bat weight.

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 692

ISSN 2229-5518

The results of this paper suggest that to limit bat performance, you must consider bat weight, bat weight distribution (e.g., moment of inertia), CoR, and characteristics of the humans swinging the bats. Similar sentiments were expressed by Nathan [15]: “bat performance depends on the interplay of the elasticity of the ball-bat collision, the inertial properties of the ball and bat, and the swing speed. It is argued that any method of determining performance needs to take all of these factors into account.” For professional baseball, the bat must be one solid piece of wood, but this no longer means that all bats must be the same shape. Professionals are allowed to drill a hole in the end of the bat, and most professionals would probably benefit from this. Next, assume that the 7 cm (3 in) at the end of the barrel of a bat is only used to “protect” the outside edge of the plate: No one hits home runs on the end of the bat. Therefore, professionals could use bats where the last 7 cm (3 in) were tapered from 2.5 in (6.4 cm) down to 1.75 in (4.4 cm). This would decrease the weight by (on average) 0.2% (generally an improvement), increase the moment of inertia about the center of mass by 0.4% (also an improvement), and would move the sweet spot. These changes would probably benefit most players but hurt others. Therefore, such modifications would have to be designed for individual players.
B. Speed of the Sweet Spot
In previous publications [3]–[5], [18], we reported the speed of the center of mass of the bat because first, the modeling is simpler, and second, the center of mass can be precisely defined. However, most other experimenters have been reporting the speed of the sweet spot of the bat. We wanted a way to relate these two pools of data, but there is no simple model that will do it. Therefore, we measured the speed of the sweet spot and the speed of the center of mass for 340 swings by 15 batters. We found speed speed (9)
with a standard deviation of 0.06. For example, if
the speed of the center of mass were 20 m/s (44 mi/h), then the speed of the sweet spot would be
23 1.3 m/s (51 3 mi/h . This variability is larger than the within-subject variability of swings of a typical
University of Arizona softball player swinging an individual bat
five times, e.g., 23 0.6 m/s 51 1.4 mi/h. The experimental data of (9) cannot be matched with a
simple model that treats the movement of the bat as a translation and a simple rotation about a
single pivot point. The movement of the bat during the swing must be described as a translation, a
rotation about the batter’s spine, and another rotation about a pivot point near the handle (whose
position may be time varying). The swing lasts
about 150 ms, depending on the speed of the swing and the definition of the beginning of the swing. The duration of the collision is 1.5–2 ms, depending on the speeds and the coefficients of restitution. For purposes of modeling the bat-ball collision, this is all condensed into one number: the speed of the collision point, which is assumed to be the sweet spot, at the time of collision.
One purpose of this paper is to show the large inter
subject variability in swinging a bat. Previous studies of variable inertia bats did not show this variability. Clutter et al. [8] had a bat speed range of 20 to 30 m/s (50 to 65 mi/h), but all seven subjects had negative slopes. Fleisig et al. [13] had typical average
bat speeds of 21 m/s (47 mi/h) with variability bars of 2 m/s. However, they averaged the data over all
17 subjects, so the individual slopes cannot be discerned.
C. Limitations
In this study, we used one simple objective function:
We found the moment of inertia that would maximize the batted-ball speed. Accuracy was not
measured. A bat with a smaller moment of inertia can probably be swung more accurately, and a bat
with a smaller moment of inertia can be accelerated faster, decreasing the duration of the
swing, thereby allowing the batter to observe the pitch longer before initiating the swing, which might
result in more accurate predictions of ball position.
Our subjects were in a laboratory swinging at a knot on the end of a string. We cannot be sure that their swings would be the same when outdoors swinging at a pitched ball. However, Crisco et al. [10] measured the swings of 19 male baseball players including nine professionals aged 17 to 39 in a batting cage. For the swings when they hit line drives, the speed of the sweet spot (which they defined to be five inches from the end of the bat) was about 30 m/s (70 mi/h) with a standard deviation of about 2 m/s. Fleisig et al. [13] measured bat speeds when hitting balls in an indoor laboratory. The average bat speed for their
17 female college softball players was 21 m/s (47
mi/h) with a standard deviation of about 2 m/s. These data fit well with our data of Fig. 2: average
21 m/s (48 mi/h) with a standard deviation of 3 m/s. Table VI shows some sweet spot speeds that have
been published. We also measured three subjects standing in the sunlight swinging bats at the home
plate of Sancet Field. Their results were not different from those recorded indoors. Our model of
the coefficient of restitution used only the shape of the object the ball collided with and the collision
speed. However, the CoR could also depend on where the ball hits the bat, because different
locations produce different vibrational losses in the

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 693

ISSN 2229-5518

bat [14]. There is also variability in the ball.We assumed that the center of mass of the ball is coincident with the geometric center of the ball. However, put a baseball or softball in a bowl of water. Let the movement subside. Then, put an X on the top the ball. Now spin it and let the motion subside. The X will be on top again.
Fig. 4. Bats can be designed with different objective functions for different batters.
This shows that for most baseballs and softballs, the center of mass is not coincident with the geometric center. Bat manufacturing for major league players has variability. Major league bats were made for us by Hillerich and Bradsby Co. The manufacturing instructions were “Professional Baseball Bat, R161, Clear Lacquer, 34 inch, 32oz, make as close to exact as possible, end brand— genuine model R161 pro stock, watch weights.” The result was six bats with weights of 32.1 oz and a standard deviation of 0.5. This large standard deviation surprised us. We assume there is the same variability in bats used by major league players. We computed the optimal moments of inertia for the batters of Fig. 2. They were members of an NCAA Division I softball team. They would all profit from using end-loaded bats. However, this might not be true for players with different skill levels.
No professional major league players participated in our variable moment of inertia experiments, and none of our bats had inertia with respect to the knob as large as major league bats. So, our conclusions may not hold for major league baseball players. All of the batters of Fig. 1 would also profit from using end loaded bats for baseball (with pitch
speeds of 38 m/s), fast-pitch softball (29 m/s), and slow-pitch softball (12 m/s).
Our conclusions are also limited to the range of inertias shown in Fig. 2.We do know what these curves would look like outside of this range. Obviously, a positive slope could not be sustained out to infinity. A sensitivity analysis is a powerful validation tool. We have done a sensitivity analysis of our model. It is most sensitive to its inputs: intercept, slope.
D. Individualization
It is now possible to design bats for individual batters. We have previously shown that it is possible to measure and compute the ideal bat weight for each individual batter. In this paper, we have shown that it is possible to measure and compute the ideal moment of inertia for each batter. Other factors of the bat design can also be determined. For example, a bat can be designed with a big sweet spot or a small sweet spot, although it is beyond the scope of this paper to discuss any of these techniques.
Average players would probably want a big sweet spot, but excellent batters would want to maximize performance for perfect hits, as is shown in Fig. 4.

6. CONCLUSIONS

To regulate bat performance, four factors must be considered: bat weight, bat weight distribution (e.g., moment of inertia), the coefficient of restitution of the bat-ball collision, and characteristics of the humans swinging the bats. Previous studies recommended light-weight bats for most batters Based on our current studies of a variety of baseball and softball players, we suggest that for each individual, there should be a moment of inertia that maximizes the batted-ball speed. There is a lot of variability in how different batters swing a bat and in how each batter swings different bats, but all the batters in this study would get higher batted-ball speeds using end-loaded bats.

7. REFERENCES

[1] R. K. Adair, The Physics of Baseball. New York: Harper&Row, 1994.
[2] , “Comment on “The sweet spot of a baseball bat,” by Rod Cross,” Amer. J. Phys., vol. 69, no. 2, pp. 229–230, 2001.
[3] A. T. Bahill and M. M. Freitas, “Two methods for recommending bat weights,” Ann. Biomed. Eng., vol. 23, pp. 436–444, 1995.

International Journal of Scientific & Engineering Research, Volume 5, Issue 12, December-2014 694

ISSN 2229-5518

[4] A. T. Bahill andW. J. Karnavas, “Determining ideal baseball bat weights using muscle force- velocity relationships,” Biol. Cybern., vol. 62, pp.
89–97, 1989.
[5] , “The ideal baseball bat,” New Scientist, vol.
130, no. 1763, pp. 26–31, Apr. 1991.
[6] P. Brancazio, SportScience: Physical Laws and Optimum Performance. New York: Simon and Schuster, 1984.
[7] , “Swinging for the fences: The physics of the baseball bat,” presented at the New England Section of the American Physical Society Meeting, Oct. 1987.
[8] J. K. Clutter and K. Koenig, “The effect of baseball-bat properties on swing speed,” in Proc. Bioeng. Conf., vol. BED-42, V. J. Goel, R. L. Spilker, G. A. Atheshian, and L. J. Soslowsky, Eds., New York, pp. 627–628.
[9] J. J. Crisco, “NCAA Research Program on Bat and Ball Performance,” Nat. Coll. Athletic Assoc.,
1997.
[10] J. J. Crisco, R. M. Greenwald, and L. H. Penna. (1999) Baseball bat Performance: A Batting Cage Study.
[11] R. Cross, “The sweet spot of the baseball bat,” Amer. J. Phys., vol. 66, pp. 772–779, 1998.
[12] , “Response to ‘Comment on The sweet spot of a baseball bat’,” Amer. J. Phys., vol. 69, no. 2, pp. 231–232, 2001.
[13] G. S. Fleisig, N. Zheng, D. F. Stodden, and J. R. Andrews, “Relationship between bat mass properties and bat velocity,” Sports Eng., vol. 5, pp.
1–8, 2002.
[14] A. M. Nathan, “Dynamics of the baseball-bat collision,” Amer. J. Phys., vol. 68, pp. 979–990,
2000.
[15] , “Characterizing the performance of baseball- bats,” Amer. J. Phys., vol. 71, pp. 134–143, 2003.
[16] F. W. Sears, M. W. Zemansky, and H. D. Young, University Physics. Reading, MA: Addison- Wesley, 1976.
[17] L. L. Van Zandt, “The dynamical theory of the baseball bat,” Amer. J. Physics, vol. 60, no. 2, pp.
172–181, 1992.
[18] R. G. Watts and A. T. Bahill, Keep Your Eye on the Ball: Curve Balls, Knuckleballs, and Fallacies of Baseball. New York: W. H. Freeman,
2000.