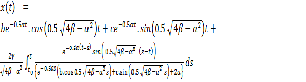The research paper published by IJSER journal is about Modeling the Electric Organ Discharge of Malapterurus Electricus Catfish 1

ISSN 2229-5518

MODELING THE ELECTRIC ORGAN DISCHARGE OF MALAPTERURUS ELECTRICUS CATFISH

HANGNILO R., ADANHOUNME V.

Abstract

This paper reports the results of modeling the electric organ discharge, (EOD) of Malapterurus electricus an ever strongly electric catfish of the sweet waters in Africa. The model will enable to design the equivalent electric scheme of the Malapterurus electricus catfish in order to allow implementations based on the electric behavior of the catfish. Malapterurus electricus EOD magnitude is sometimes over 350 V. It’s a true source of energy worthy of interest. Comparing Malapterurus electricus EOD to the electric discharge of the given model points out an encouraging similarity. The model is beforehand electromechanical one. Its survey has allowed designing an equivalent electric scheme capable to deliver some electric discharge in the way of Malapterurus electricus catfish. Hence electric catfish applications become more accessible.

Key words: Malapterurus electricus, EOD, electric equivalent model, electric dipole, electrostatics.

Introduction

Malapterurus electricus is a typical electric catfish of fresh water in Africa, [1], [2]. This kind of fish is widespread in fresh water in Benin Republic like Zou and Ouémé River, [3]. The Republic of Benin is in a deep lack of energy. Many households in the country are deprived of every electric convenience. A major part of energy consumed in Benin comes from abroad. The provider of electric energy to the country is CEB, (la Communauté Electrique du Bénin). The CEB buys itself energy outdoor: on December
31st 2004 the imports from Vra, (Volta Region Authority in
Ghana) and from Cie, (la Compagnie Ivoirienne
d’Electricité) amount to 1,050.866 GWh, [4]. Malapterurus electricus is able to produce electric discharges taking sometimes over 350 volts, [5]. It’s a true source of energy worthy of scientific interest. The proof is given on figure 1 where a LED is switched on with the help of the catfish in our Laboratory. Despite the availability of such pollution free renewable energy source there is no more solution concerning a widespread use of energy from electric catfish in general as well as from Malapterurus electricus in particular.
That’s why the given catfish has been chosen for our study which consists of determining an equivalent electric scheme of the fish. With the help of that scheme we can exploit rationally the energy of Malapterurus electricus catfish. In fact the equivalent electric model will
allow plugging the catfish as a power supply to an electric load.

Fig. 1. Malapterurus Electricus catfish switching on a LED

Therefore we can master the EOD of the catfish without any nuisance for them. The reproduction of Malapterurus electricus EOD by the model will permit some electrostatic therapies without resorting to the catfish. The ways of struggle proper to the electric catfish are going to be improved.
In the second section the hypothesis is done on the dipole
nature of the catfish. Here the electro mechanical model and the analytical modeling of Malapterurus electricus have been designed. In the third section a computer simulation in Matlab of the equivalent electric models of Malapterurus electricus catfish and the analysis of the results of the simulations have been tackled. Then we bring the study to a close.

2. Materials and methods

On watching some animals such as cow, goat, or sheep etc, we can notice that they move their tail or make vibrate all their body or some part of their body to prevent the flies from upsetting them. Taking into account that fact and the electric behavior of the catfish we imagine the Malapterurus electricus electromechanical equivalent model under the shape of an electric dipole whose unlike electric charges of equal

The research paper published by IJSER journal is about Modeling the Electric Organ Discharge of Malapterurus Electricus Catfish 2

ISSN 2229-5518

magnitude q are linked by a spring of stiffness k, figure
2. The length d=2(a + x) of the dipole depends on the time, 2a is the distance that separates the electric charges
when the elongation x (t) of the spring equals to zero.

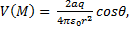
2.2- Mathematical model

(1)

That is the oscillating electric dipole. The model leads to a differential non linear equation of second order that we call the oscillating electric dipole equation. The equivalent electric scheme we are searching for is established with the help of the solution to that equation. When other animals have claws and teeth to defend and feed themselves, electric catfish have not those tools but they got their EOD that they modulate into extend as well as into frequency considering the case. To reach the goal of the study we need a power supply, a digital multiplier circuit AD734AN type, a computer equipped in Matlab software and some diodes.

Fig. 2. Electromechanical model of

Malapterurus electricus

2.1- Hypothesis of electric dipole model

Fig. 3. Electric dipole model of

Malapterurus electricus catfish

The two charges of the electric oscillating dipole are –q and +q possessing masses m1 and m2 such that m1 = m2 = m, (see figure 2).
The statement of the analytical expressions of the main
forces acting on these charges is done in [7] where we obtain the equation of that particular dipole as follows:

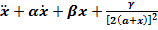= 0, (3)

Where:

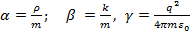, (4)

We have solved (3) under the following initial conditions: 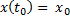, 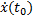= 0, (5)

3- Results and discussion

3.1- The model in the case when 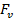= 0.

When 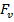= 0, α = 0 and the equation (2) reduces to:
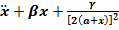= 0, (6) Assuming that a is negligible with respect to x, the equation (6) reduces to:

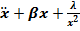= 0, where λ = γ/4, (7)

For equation (7), we obtain the following analytical solution:

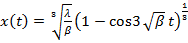, (8) Putting (8) into (1) we obtain the electric potential V (M) that expresses the electric behavior of the catfish:

Malapterurus electricus catfish is out of hypothesis a
network of electric dipoles with a steady electric dipole moment. Two equal charges, q, of opposite sign separated by a distance 2a, constitute an electric dipole, [6]. The
electric potential of an electric dipole, (figures 2 and 3) is

3.2- Single electric dipole case

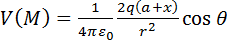
, (9)

V (M) provided only that the point M(r, ѳ) is not closer to the dipole:
From the starting point, we consider a unique oscillating
electric dipole. The implementation of formula (9) gave a result that is close to a twofold alternation straightening

The research paper published by IJSER journal is about Modeling the Electric Organ Discharge of Malapterurus Electricus Catfish 3

ISSN 2229-5518

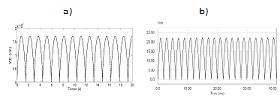
rectifier, (figure 4-a). This deduction enabled us to finalize the equivalent electric circuit in the form of a Graetz Bridge rectifier, (figure 5-a) (or a centered point transformer rectifier, figure 5-b). The output voltage (figure 4-b) of each equivalent electric scheme (figure 5-a, b) is of course close to the electric discharge of the electromechanical model, (figure 4-a).

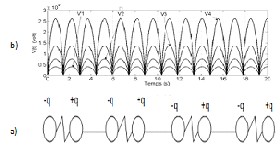
Fig. 6. Simulation of the model of four like dipoles

Fig. 4. Results of the unique dipole model

a- Potential difference of the oscillating dipole

b- Output voltage of the equivalent electric scheme

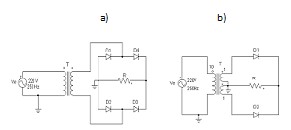
Fig. 5: Equivalent electric scheme of the catfish for FV=0

3.3- The n-oscillating dipoles study

Then we have simulated the behavior of four like dipoles (figure 6-a). In this case the polar coordinates r and θ of the point M related to each electric dipole are in Tab.1. Simulating that model we got some results that tally with the reality. Indeed the model varies the magnitude of its electric discharges in the way of the catfish (figure 6-b).

Tab1

Polar coordinates of M according to each dipole

3.4 The model in the case when 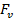≠ 0

The solution given by the Adomian decomposition technique to equation (2

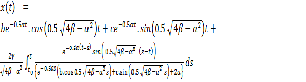(10

)

Where:

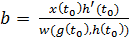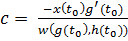; , (11)

The electric potential of the oscillating dipole is:

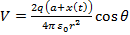, (12)

A computer simulation of (12) gives the result in figure 7- a.

Fig. 7: a-EOD of the electromechanical model with α=0.0001, β=100 and γ=0.0001

b- EOD of the high fidelity simulator in figure 8; c-EOD of

Malapterurus electricus catfish.

The research paper published by IJSER journal is about Modeling the Electric Organ Discharge of Malapterurus Electricus Catfish 4

ISSN 2229-5518

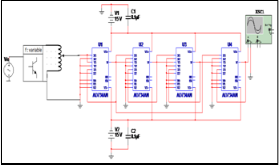
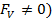
Fig. 8. High fidelity simulator of the EOD of Malapterurus electricus, (

According to the value of the viscous friction force FV, we got two equivalent models for the electric behavior of the catfish. For FV = 0 the first analytical model is relation (8). The simulation of that model in Matlab gives a potential difference (figure 4-a) which is similar to the EOD of the fish, (figure 7-c) and to the output voltage of a regular Graetz bridge rectifier (figure 4-b). As a consequence we set up the first electric equivalent scheme of Malapterurus electricus as a Graetz bridge rectifier (figure 5-a). Then we have considered the catfish as a network of four oscillating electric dipoles with a steady electric dipole moment. The simulation of four like dipoles (figure 6-a) gave a result which sticks to reality: by baiting respectively j (j=1, 2, 3, 4) dipoles out of n, (n=4) the model produces some EOD with unsteady amplitudes as Malapterurus electricus does (figure 6-b). Taking advantages from those results, we have designed an electromagnetic weapon that destroys anopheles ‘larvae in fresh water to control malaria disease burden in every endemic area. Taking into account the viscous friction force Fv the second analytical model of the catfish can be described by (11) as the electric potential due to the oscillating electric dipole at any point of the space. A computer simulation of the potential difference due to that model gave the result in figure 7-a. That electric wave is closer to the EOD of the catfish and leads into the high fidelity equivalent electric scheme of the fish in figure 8. The response of this last model (figure 7-b) is very close to the EOD of the catfish as to the oscillating dipole behavior.

Conclusion

We consider that the goal of our study is reached. The similitude between Malapterurus electricus’ EOD and the output voltage of the equivalent electric schemes we got for that catfish is outstanding. The output voltage of a rectifier using a middle point transformer or a regular
Graetz bridge is similar to the potential difference created
in two different points of space by a swaying electric dipole as figures 4-a, b and 6-b have shown. With the help of an autotransformer we can vary the magnitude of the output signal of the equivalent electric scheme, (figure 5) in the way of the fish. Varying the frequency of the voltage reference of a PWM inverter we can succeed in modulating the frequency of the output wave of the model to imitate the fish very well, (figure 8). Malapterurus electricus EOD can kill or heal. The electromagnetic weapon equipped with the equivalent electric scheme of the catfish in figure 5 destroys anopheles ‘larvae in fresh water as spectacularly as Malapterurus electricus does. Formerly Egyptian cured some sickness using the electric shocks of Malapterurus electricus. A similar application can be developed using the high fidelity simulator in figure 8. A management of the power generated by Malapterurus electricus becomes easy with the help of the first analytical model of the catfish. Hence the equivalent electric models that we have set up are quiet suitable and very useful.

References

[1] Rankin CH, Moller P (1992), Temporal patterning of electric organ discharges in the African electric catfish, Malapterurus electricus. J Fish Biol 40 (1): 49-58.

[2] Sagua VO (1979), Observations on the food and feeding habits of the African electric catfish, Malapterurus electricus. J of Fish Biol 15 (1): 61-69.

[3] Projet de pêche lagunaire au Bénin, (1993) Guide de détermination des poissons et crustacés des lagunes et lacs du bas Bénin: 90-120 Cotonou.

[4] Communauté Electrique du Bénin, (2004), CEB as a supplier of energy to fuel economies and cooperation between countries at the sub-regional level, Annual Report, 19-36.

[5] Klas-Bertil A, Alf GJ (1958), The Acetylcholine system of electric organ of Malapterurus electricus. J. Physiol 140: 498-500.

[6] Halliday D, Resnick R (1974) Fundamentals of Physics. John

Willy & Sons Inc, New York.

[7] Hangnilo R, Adanhounme V (2012) Solving the oscillating electric dipole equation by Adomian decomposition tec hnique. IJSER Volume 3, Issue 5, May-2O12.

Hangnilo Robert received the M.Sc. degree in Energy Power & Motion Control in Energy Institute of Moscow and the Ph.D. degree in the University of Havre in France.

He is currently Assistant Professor of Electromagnetism and Energy Systems Implementations at the ‚Ecole Polytechnique d’Abomey- Calavi‛ - University of Abomey-Calavi in Benin Republic.

The research paper published by IJSER journal is about Modeling the Electric Organ Discharge of Malapterurus Electricus Catfish 5

ISSN 2229-5518

His principal research interests are Modeling of Energy systems and vector Control in Malaria.

E-mail: hangnilo555@yahoo.fr

Villevo Adanhounme received the M.Sc. and Ph.D. degrees in mathematics from the Russian People University of Moscow.

Russian Federation. He is currently Assistant Professor of variational

calculus and advanced probability at the International Chair of Mathematical Physics and Applications – University of Abomey Calavi. Benin.

His principal research interests are applied mechanics,

Partial differential equations and optimal at the International Chair of Mathematical Physics and Applications.

E-mail: adanhuonm@yahoo.fr