International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1660
ISSN 2229-5518
Methods for data assimilation for the purpose of forecasting in the Arabian Sea
Gaurangi Prajapati, Dr.H M Patel, Rakesh Shah, Avinash Shah and Anil Kadia
Abstract— Fluid dynamics, wind wave modeling describes the effort to depict the sea state and predict the evolution of the energy of wind waves using numerical techniques. These simulations consider atmospheric wind forcing, nonlinear wave interactions, and frictional dissipation, and they output statistics describing wave heights, periods, and prop- agation directions for regional seas or global oceans. forecast has been a key area of investigation and if certain methods can be plotted in order to help in improvement of the forecast it would be salutary
to the development in this direction .
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
Index Terms--Arabian Sea,Ocean data Assimilation, Climat Change,Kalman Filter, Quasi Geostrophic.
![]()
![]()
•
1661
1 INTRODUCTION
1 --G ER IS) 2014
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1662
ISSN 2229-5518
The Arabian Sea is a region of the Indian Ocean bounded on the north by Pakistan and Iran, on the south by northeastern Somalia, on the east byIndia, and on the west by the Arabian Peninsula. Some of the ancient names of this body of water in- clude Sindhu Sagar (meaning "Sea of Sindh" in San- skrit) and Erythraean Sea.
The Arabian Sea's surface area is about 3,862,000 km2 (1,491,130 sq mi). The maximum width of the Sea is approximately 2,400 km (1,490 mi), and its maximum depth is 4,652 metres (15,262 ft). The biggest river flowing into the Sea is the Indus River.
The Arabian Sea has two important branches — the Gulf of Aden in the southwest, con- necting with the Red Sea through the strait of Bab-el-Mandeb; and the Gulf of Oman to the northwest, connecting with the Persian Gulf. There are also the gulfs of Cambay and Kutch on the Indian coast.![]()

Arabian Sea from space
The Arabian Sea has two important branches — the Gulf of Aden in the southwest, con- necting with theRed Sea through the strait of Bab-el-Mandeb; and the Gulf of Oman to the northwest, connecting with the Persian Gulf. There are also the gulfs ofCambay and Kutch on the Indian coast.
17th century map depicting the locations of the Periplus of the Erythraean Sea
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1663
ISSN 2229-5518
The countries with coastlines on the Arabian Sea are Somalia, Djibouti, Yemen, Oman, Iran, Pakistan, Indiaand the Maldives. There are sev-
eral large cities on the sea's | coast | includ- |
ing Karachi, Gwadar, Pasni,Ormara, Aden, Muscat, Mumbai, Keti | Ban- | |
dar, Salalah and Duqm. |

The Arabian Sea is a sea located to the north of the Indian Ocean. Tropical cyclones in the basin are abbreviated ARB by the India Meteorological Department (IMD), the offi- cial Regional Specialized Meteorological Centre (RSMC) of the basin.
The Arabian Sea's coast is shared among India, Yemen, Oman, Iran, Pakistan, Sri
Lanka, Maldives and Somalia.
Monsoons are characteristic of the Arabian Sea and responsible for the yearly cycling of its waters. In summer, strong winds blow from the southwest to the northeast, bringing rain to the Indian subcontinent. During the winter, the winds are milder and blow in the opposite direction, from the northeast to the southwest.
Cyclones are very rare in the Arabian Sea, but the basin can produce strong tropical cy- clones. An example is Cyclone Gonu, the strongest recorded tropical cyclone in the basin.
The list below contains the 11 strongest tropical cyclones in terms of atmospheric pres- sure which have formed over the Arabian Sea since 1990.
No. | Name | Lowest Pressure (mbar) | Year | Image |
01 | Gonu | 920 | 2007 |
|
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1664
ISSN 2229-5518
No. | Name | Lowest Pressure (mbar) | Year | Image |
02 | ARB 01 | 932 | 2001 |
|
03 | ARB 01 | 946 | 1999 |
|
04 | ARB 02 | 958 | 1998 |
|
05 | Phet | 970 | 2010 |
|
06 | ARB 01 | 972 | 1996 | N/A |
07 | 05A | 976 | 1996 |
|
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1665
ISSN 2229-5518
No. | Name | Lowest Pressure (mbar) | Year | Image |
08 | 02A | 977 | 2003 |
|
09 | ARB 02 | 980 | 1994 |
|
10 | ARB 04 | 984 | 1994 | N/A |
11 | Phyan | 988 | 2009 |
|

The Arabian Sea is a northwestern extension of the Indian Ocean, positioned between In- dia, Oman, Pakistan and Yemen, and Cape Guardafui in far northeastern Somalia.
The sea connects with the Persian Gulfthrough the Gulf of Oman and the Strait of Hormuz. In the southwest, the Gulf of Aden connects it with the Red Sea.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1666
ISSN 2229-5518
The most significant ports in the Arabian Sea include Karachi, Pakistan, and Mumbai, In- dia.
It has an estimated area of approximately 1,491,000 sq miles (3,862,000 sq km) and an es- timated average depth of 8,970 feet (2,734 m). The southern border is amapping opinion of Graphic Maps.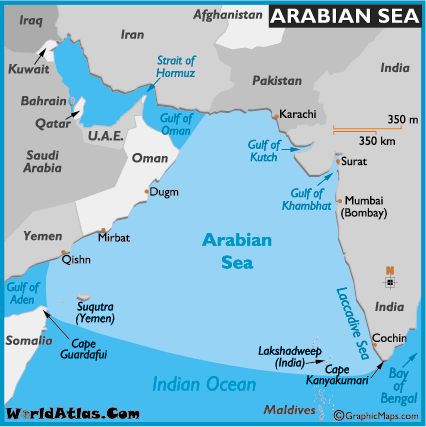
![]()
The Gulf of Kutch is an inlet of the Arabian Sea along the west coast of India, in the state of Gujarat, and renowned for extreme daily tides .
The maximum depth of Gulf of Kutch is 401 feet (122 m).
It is about 99 miles in length, and divides Kutch and the Kathiawar peninsula regions of
Gujarat. The Rukmavati River empties into the Arabian Sea nearby.
Most of the Arabian Sea has depths that exceed 9,800 feet (2,990 metres), and there are no islands in the middle. Deep water reaches close to the bordering lands except in the north- east, off Pakistan and India. To the southeast the Lakshadweep atolls form part of the sub- marine Maldives Ridge, which extends farther south into the Indian Ocean where it rises above the surface to form the atolls of theMaldives. On the western side of the sea, the plateau island of Socotra, about 70 miles (110 km) long and with an area of about 1,400 square miles (3,625 square km), is an insular extension of the Horn of Africa, lying 160 miles (260 km) east of Cape Gwardafuy (Guardafui).![]()
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1667
ISSN 2229-5518
Climate:
The Arabian Sea has a monsoon climate. Minimum air temperatures of about 75 to 77 °F (24 to 25 °C) at the sea’s surface occur in the central Arabian Sea in January and February, while temperatures higher than 82 °F (28 °C) occur in both June and November. During the rainy season, which occurs when the southwest monsoon winds blow (April to November), salinities of less than 35 parts per thousand have been recorded in the upper 150 feet (45 metres) of the sea, while during the dry season (November to March), when the northeast monsoon winds blow, salinities of more than 36 parts per thousand have been recorded at the surface over the entire Arabian Sea north of latitude 5° N, except off the Somali coast. Because evaporation exceeds the combined precipitation and riverine input, the sea exhibits a net water loss annually.
The complex Somali Current, which attains speeds of about 7 knots (8 miles [13 km] per hour) off the coast of Socotra, becomes part of a clockwise circulation system that in sum- mer continues to the northeast along the coast of Arabia and thence south along the coast of India to 10° N. At that point it merges with the Southwestern Monsoon Current, flowing east between 5° and 10° N. Pronounced upwelling of deeper waters occurs along the Soma- li and Arabian coasts in summer. The Somali Current weakens and reverses direction dur- ing the northeast (winter) monsoon. Of the five water masses that have been distinguished in the upper 3,000 feet (900 metres) of the northern Indian Ocean, three have been identi- fied as originating in the Red Sea, the Persian Gulf, and the Arabian Sea, respectively. The paths of flow of these water masses are to the south and east.
Ocean data assimilation is a general methodology for estimating values for dynamically evolving oceanic variables by combining the information contained in dynamical ocean models and in observational data. This combination of information generates an estimate of the current state of these variables – an analysis – which may then be used as an initial condition for later numerical forecasting of future ocean conditions. The complex relation- ship between the various relevant dynamic variables in the ocean produces a chaotic pattern to the growth, with time, of measured differences between forecasts generated from similar initial conditions. Hence the accuracy of analyses is one of the key factors limiting the ac- curacy of ocean forecasting as a predictive tool.
Many current data assimilation methods are based upon the concept of a ‘most-likely’ esti- mate, a representative state that has the greatest probability of having occurred, given pre- vious forecasts and the result of all available observations. The analysis thus represents the modal state of any forecast ensemble and, it is argued, the best viable choice for an initial
condition for future deterministic forecast. Analogy can be drawn with the parameterization
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1668
ISSN 2229-5518
of small scale mixing processes. There exist myriad possible arrangements of a dynamic var- iable on scales well below that being modelled. However if an assumption is made as to the probability density of the various arrangements (as is made for example in the mathematical modelling of Brownian motion) and the most likely estimator of the states assumed true (in this case through application of the central limit theorem), then a modelling assumption is generated (Fickian diffusion) which is applicable on the scales of interest.
.
The Arabian Sea is a region of the Indian Ocean bounded on the north by Pakistan and Iran, on the south by northeastern Somalia, on the east byIndia, and on the west by the Arabian Peninsula. Some of the ancient names of this body of water in- clude Sindhu Sagar (meaning "Sea of Sindh" in Sanskrit) and Erythraean Sea.
The Arabian Sea's surface area is about 3,862,000 km2 (1,491,130 sq mi). The maximum width of the Sea is approximately 2,400 km (1,490 mi), and its maximum depth is 4,652 metres (15,262 ft). The biggest river flowing into the Sea is the Indus River.
The Arabian Sea has two important branches — the Gulf of Aden in the southwest, con- necting with the Red Sea through the strait of Bab-el-Mandeb; and the Gulf of Oman to the northwest, connecting with the Persian Gulf. There are also the gulfs of Cambay and Kutch on the Indian coast.
An IJSER copyright form must accompany your final submission. You can get a .pdf, .html, or .doc version at
http://computer.org/copyright.htm. Authors are responsible for obtaining any security clearances.
For any questions about initial or final submission requirements, please contact one of our staff members. Con- tact information can be found at: http://www.ijser.org.
————————————————
• Gaurangi Prajapati is currently pursuing doctoral degree program in mathematics in Pacific University, India,.
• Dr.H M Patel is currently Principal-(I/C) in Bhavans Science College,
Ahmedabad India,
Statistical methods require assumptions on the distributions to be represented. In the case of da- ta assimilation this requires the spatial covari- ances within variable fields and the correlations
in the behaviour between different variables.
Generally there is not enough data to estimate these accurately. Often these distribu- tions are chosen on an ad hoc basis to represent known physical relationships, such
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1669
ISSN 2229-5518
as geostrophy.
An alternative approach is to apply these relationships directly, as expressed in the dynamic equations, when creating an assimilation method. This is similar to the phi- losophy behind the introduction of a variety of ‘adiabatic’ techniques for sub-grid pa- rameterizations, such as the Gent and McWilliams (1990) method. These adiabatic
parameterization methods have been found (Danabasoglu et al., 1994; B¨oning et al.,
1995) to give better fit to observations and more stable results when used for large- scale ocean modelling than schemes which pay less heed to con-served properties. The subject of this thesis is a discussion of a similarly adiabatic approach in the con- text of ocean data assimilation and the ocean inverse problem.
The traditional data assimilation methods, with particular reference to the atmos- phere, see the textbooks of Daley (1991) or Kalnay (2002). Ghil and Malanotte- Rizzoli (1991) contains a detailed, if slightly dated, discussion of current methods in data assimilation for geophysical fluids. A book by Wunsch (1996) develops the discretized inverse problem in the context of ocean dynamics and discusses the dif- ficulties of the state estimation problem.
The atmosphere and the ocean are two typical fluids on the Earth. Their behaviors
directly affect the life and activities of human beings. To efficiently predict their fu- ture behaviors is very important. Since the advent of more powerful computers,
higher-resolution atmospheric models and oceanic models have been developed. These models have shown a remarkable capability to predict some key phenomena
and to simulate some important characteristics of the atmosphere or ocean. All of the models, however, require a complete and accurate specification of the three-
dimensional (3D) structure of the initial state of a considered system. Besides con- ventional data (radiosonde, surface, and dropsonde data, mainly), many new
sources of data, such as satellite data, radar, profilers, and other remote-sensing de- vices, have become available. However, observations are still sparse, and it is still
impossible to measure all of the model's degrees of freedom at a given time. In ad- dition, the observations are irregularly distributed in space and time, and they have different structures of random error. Therefore, an efficient data assimilation meth- od is needed to combine these irregular observations to generate the initial condi- tions that are distributed on regular model grids.
The development of data assimilation methodology has mainly experienced three stages: simple analysis, statistical or optimum interpolation, and variational analy- sis. Simple analysis methods were mostly used in 1950s, when computers were un- available or at the beginning stage. Simple analysis methods were the earliest bases of data assimilation. In the 1960s and 1970s, statistical considerations were intro- duced into the atmospheric data assimilation. Based on these considerations, some forms of optimum interpolation were used to assimilate observations into forecast models. These optimum interpolation analysis methods were used in many opera- tional centers worldwide. In the 1980s and 1990s, atmospheric data assimilation switched to variational methods, in particular the three- and four-dimensional varia- tional data assimilation (3D-Var/4D-Var) by using adjoint techniques. The 3D- Var/4D-Var approaches attempt to combine observations and background infor- mation in an optimal way to produce the best possible estimate of the model initial state. This technique not only has broad applications for the assimilation of atmos- phere and ocean, but also can be used for many other applications in numerical
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1670
ISSN 2229-5518
weather prediction.
Data assimilation plays a more and more important role in numerical weather pre- diction, and it is considered as a frontier branch of atmospheric and oceanic scienc- es. In this paper, three examples are presented to illustrate (i) the use of new types of observations, and (ii) the ability to improve the forecast skill of numerical weath- er prediction.
Global Positioning System (GPS)/Meteorology (MET) Data Assimilation:
With the advent of the GPS by using high performance transmitters in high orbits and low earth orbiting satellites equipped with GPS receivers, it is now possible to remotely sound the Earth's atmosphere by using radio occultation techniques (1–2). A prototype demonstration of this capability has been provided by the GPS/MET experiment. Although it was shown that high vertical resolution profiles of atmos- pheric refractivity, temperature, and geopotential height at constant pressure levels can be derived from the GPS measurements, with high accuracy under many cir- cumstances, many issues remain. These issues include the existence of multipath propagation, the ambiguity between water vapor and temperature in moist regions of the atmosphere, and the difficulty in retrieving an accurate refractivity profile from the GPS refraction angle measurements over regions where the horizontal gra- dient of the refractivity is large. For this reason, a methodology for incorporating the GPS “raw” measurements (refraction angles) directly into numerical weather analysis and/or prediction systems is required and has been developed. It includes a ray-tracing observation operator that converts the atmospheric state variables to the GPS refraction angle measurements, and its tangent linear and adjoint operators. These three operators are required for the direct use of GPS refraction angle meas- urements in a variational data analysis system.
A twin least-square-fit experiment incorporating simulated GPS refraction angles is then conducted. The cost function converges to a known minimum, which shows that the development of the tangent linear and adjoint versions of the ray-tracing observation operator and the linkage to the National Centers for Environmental Prediction (NCEP) global analysis are carried out correctly in this idealized case. Also, an analysis of all of the real GPS refraction angle measurements available from the GPS/MET experiment over a selected 12-h period is carried out. The changes made to the NCEP temperature, specific humidity, and pressure fields as a result of the minimization of two cost functions measuring the distance between the model-simulated and the observed GPS/MET refraction angles in two 6-h time windows suggest (i) a positive adjustment in the NCEP temperature field in the up- per atmosphere between 15 km and 30 km; (ii) a negative adjustment of the mois- ture field in the lower troposphere below 500 hPa; and (iii) a negative adjustment of pressure field throughout the entire atmosphere up to about 20 km. This study also indicated that use of GPS refractivity might produce errors in the lower troposphere, where the refractivity gradient is large.
The major difference between the traditional method and method of assimilation which is hy- pothesised is that it is more accurate and advanced and can help in the mathematical model formation in dealing with the assimilation.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1671
ISSN 2229-5518
• J.Icarus Allen, J. R. Siddorn, J. C. Blackford, and F. J. Gilbert. Turbulence as a control on the microbial loop in a temperate seasonally s tr a tie d marine sys- tems model. J. Sea Res., 52:120, 2004.
• S. P. Anderson and R. A. Weller. Surface buoyancy forcing and the mixed layer of the western P aci c warm pool: Observations and 1d model results. J. Climate, 9:30563085, 1996.
• S. Akella and I. M. Navon. A comparative study of high resolution advection schemes in the context of data assimilation. International Journal for Numerical Methods in Fluids, 51:719–748, 2006.
• A. Arakawa and V. R. Lamb. A potential enstrophy and energy conserving scheme for the shallow water equations. Monthly Weather Review, 109:18–36, January
1981.
• A. Arakawa and V. R. Lamb. Computational design of the basic dynamical processes of the UCLA general circulation model. Methods in Computational Physics, 17:
173–265, 1977.
• N. Ayoub. Estimation of boundary values in a North Atlantic circulation model us- ing an adjoint method. Ocean Modelling, 12(3–4):319–347, 2006.
• I. J. Barton. Satellite-derived sea surface temperatures: Current status. Journal of
Geophysical Research, 100(C5) :8777–8790, May 1995.
• G. K. Batchelor. An Introduction to Fluid Dynamics. Cambridge University Press,
1967.
• M. J. Bell. Momentum fluxes in the Bryan/Cox ocean circulation model. Journal of
Atmospheric and Oceanic Technology, 15(6):1400–1413, December 1998.
The primary interest of mathematicians, dating back to the first synoptic charts drawn up by Admiral Robert Fitzroy in the 1860s, was to accurately determine the transient state of the atmosphere. Climatological data represented primarily a useful ‘first guess’ for the more im- portant question of the current weather patterns. In keeping with this philosophy, the goal in
atmospheric data assimilation has typically been to use the information contained in meteor-
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1672
ISSN 2229-5518
ological observations to produce an accurate estimate of the current state of the atmosphere
- an analysis field.
In contrast with this, work in the oceanographic community was historically directed to- wards coupling modelling, theory and observations to determine an estimate of the mean state of the ocean, often termed state estimation or inverse modelling. The difference be- tween these two viewpoints is predominantly in terms of timescale. The aim of state estima- tion is to recover the long-term time average of the ocean state from long, gappy, series of ocean observations, with the available observations often widely separated in space and time. A necessary condition for this method to succeed is the existence of a well-defined sta- tionary mean state, upon which intra-decadal variations appear as small-scale noise. Data as- similation is intimately coupled with the idea of forecasting the magnitude of the transient magnitudes of these small-scale deviations. Early oceanographic work was focused on the area of state estimation for several principle reasons:
(i). Accurate measurements of dynamically important oceanic variables such as tempera- ture and salinity were (and to a certain extent remain, see section 1.4) difficult and expensive to obtain, hard to record and time-consuming to collate. This means that the historical data set available to investigators is small, with poor temporal and spa- tial coverage, especially in the Southern Ocean.
(ii). It was for a long time believed, following the theory of Ekman (1905), Sverdrup (1947), Munk (1950) and others, that the observed ocean state could be almost entire- ly explained through a combination of largely static flow in the interior maintaining geostrophic and hydrostatic balance, with primarily wind driven circulations near the surface. This concept of steady ocean currents, “Rivers in the Sea”1, assumes that the transient signal is small and dynamically unimportant, except possibly for the case of the external wind forcing, which may itself be derived from meteorological observa- tions.
The ocean has a much smaller Rossby number than the atmosphere in most areas and
situations. This non-dimensional number governs the length scale at which geostrophic balance holds. This means that significantly higher spatial resolutions are required to model important mesoscale features, such as mesoscale eddies or transient displace- ments of the thermocline, which are of interest to end-users such as fisheries and na- vies. Until recently limitations on available computing resources were such that stand- ard models could not run with grid spacing such that they could resolve these length- scales.
(iv). The observational and model data available at the time supported the idea of a quies- cent ocean. In fact the ocean was typically believed laminar in its interior, until this
assumption was cast into doubt by accumulated observational data in the 1970s. The
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1673
ISSN 2229-5518
unprecedented large-scale and near synoptic observations of the World Ocean Circula- tion Experiment (WOCE) from 1990 until 1998 exploded this myth, with turbulent structures and great temporal and spatial variability being detected with ubiquity.
Among the earliest attempts at what may be termed ocean state estimation, aiming at de- termining the long term ocean state, are the discovery of the location and approximate strength of the ocean surface currents by various groups of seafarers, starting with the dis- covery of the Canary and Guinea Currents by Portuguese sailors in the 15th century (Krauss, 1996). Differences were observed between a ship’s apparent positions calculated from their course and speed through the water, ‘dead reckoning’, and the ship’s actual posi- tion, as derived from celestial observations. These differences were then ascribed to drift due to surface currents, with repeated observations allowing the flow to be mapped.
This is a specific example of the general class of inverse problems. Both the data assimila- tion problem for ocean forecasting and state estimation of the ocean fall into this classifica- tion. Given a general mathematical operator, the black box of high school mathematics, ac- cepting inputs from one set of data and mapping them in some fashion consistently to anoth- er, the outputs.
T R A DI T I O N AL D AT A A S S IM IL AT IO N M E T HODS
The theory behind the derivation of the BLUE equation forms the basis for many modern assimilation techniques, including the Kalman filter, Kalman smoother, 3D-VAR and 4D- VAR techniques. Many operational ocean forecasting centres use variations on these meth- ods. For example, the UK Met Office Forecasting Ocean Assimilation Model (FOAM) uses an Analysis Correction Method (ACM) (Lorenc et al., 1991) to assimilate temperature and salinity profiles. The basis of the ACM is an iterative approximation converging to the BLUE analysis described below. The European Centre for Medium-range Weather Forecast- ing (ECMWF) uses a 4D-VAR scheme for its operational ocean model, run to assimilate ob- servations over a ten day time window.
The overall focus of this thesis is:
To understand the benefits and issues involved in using phase error assimilation methods in a general, mathematically rigorous and physically consistent ocean fore-casting system.
To what extent is it feasible to decouple the observed error signal in ocean anal- yses consistently into signals due to pure phase error and amplitude error?
Given that real oceanographic observations are noisy and limited in scope and number, can a study of novel phase correction algorithms give a quantitative un- derstanding of how observations relate to model data in such methods and what
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1674
ISSN 2229-5518
constraints on observations are required?
Is it possible to develop efficient algorithms which maximise the utility of dis- placement assimilation techniques, for example in terms of the use of the infor- mation contained within observations, in the same way that 4D-VAR methods al- low the use of multiple nonlinear observations taken at different times?
The identical twin methodology is to be used to investigate the methods and then details the approximations made in the quasi-geostrophic model used in the numerical experi- ments.. Following the derivation of the model and a description of its behaviour we con- clude by justifying the choices and methods to be used to generate the numerical model and initial conditions used to form ‘true’ and ‘observational’ data in the data assimilation experiments.
Two of the most important and general of these approximations are:
i. The continuum approximation. Rather than modelling individual molecular mo- tions, the fluid is modelled as a continuous medium and it is assumed that the Navier- Stokes equations apply.
ii. Incompressibility. On the horizontal and length-scales of interest to oceanographers changes in density due to pressure variations are negligible. This means the velocity field in the flow is effectively solenoidal (Batchelor, 1967).
The IJSER style is to create displayed lists if the number of items in the list is longer than three. For example, with- in the text lists would appear 1) using a number, 2) followed by a close parenthesis. However, longer lists will be formatted so that:
1. Items will be set outside of the paragraphs.
2. Items will be punctuated as sentences where it is appropriate.
3. Items will be numbered, followed by a period.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1675

ISSN 2229-5518
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1676
ISSN 2229-5518

A simple schematic showing the difference between layer models, in which the thicknesses of layers, such as the one shaded in grey are stored along with other dynamical properties on a horizontal discretization structure, and level models where properties such as vertical velocity are stored on a vertical discretization divided as by the dotted lines.
Appendixes, if needed, appear before the acknowledgment. In the event multiple appendices are required, they will be labeled “Appendix A,” “Appendix B, “ etc. If an article does not meet submission length requirements, authors are strong- ly encouraged to make their appendices supplemental material.
IJSER Transactions accepts supplemental materials for review with regular paper submissions. These materials may be published on our Digital Library with the electronic version of the paper and are available for free to Digital Library visitors. Please see our guidelines below for file specifications and information. Any submitted materials that do not follow these specifications will not be accepted. All materials must follow US copyright guidelines and may not include material previously copyrighted by another author, organization or company. More information can be found at http://www.ijser.org.
I am thankful to Pacific University for their Cooperation in this Paper and am also obiliged as Dr H M Patel hads been very kind in considering me as his student for guiding me in this endevour.I am thankful to Ms Sanchita Mitra for being my emotional anchor.And last not the least I am thankful to my family for their support.
Unfortunately, the Computer Society document translator cannot handle automatic endnotes in Word; therefore, type the reference list at the end of the paper using the “References” style. See the IJSER’s style for reference for- matting at: http://www.ijser.org transref.htm. The order in which the references are submitted in the manuscript is the order they will appear in the final paper, i.e., references submitted nonalphabetized will remain that way.
Please note that the references at the end of this document are in the preferred referencing style. Within the text,
use “et al.” when referencing a source with more than three authors. In the reference section, give all authors’ names; do not use “et al.” Do not place a space between an authors' initials. Papers that have not been published should be cited as “unpublished” [4]. Papers that have been submitted or accepted for publication should be cited as “submitted for publication” [5]. Please give affiliations and addresses for personal communications [6].
Capitalize all the words in a paper title. For papers published in translation journals, please give the English citation first, followed by the original foreign-language citation [7].
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1677
ISSN 2229-5518
Additional information on formatting and style issues can be obtained in the IJSER Style Guide, which is posted online at:
http://www.ijser.org/. Click on the appropriate topic under the Special Sections link.
Conservation properties and phase error are closely related areas in which standard data assimilation algorithms may fail. There are several approaches which can act to alleviate this problem. The aim of this thesis has been to understand the benefits and issues involved in using phase error correction methods in a general, mathematically rigorous and physically consistent ocean forecasting system.
Most previous development in this area has been based in the context of extremely well observed systems. Here the approach has been to extend towards problems with limited observations and to examine destructive- ly under what conditions such approaches fail. This is first performed for an algorithm based on the descent of a spatial cost-function analogous to 3D-VAR.
A novel approach based on a four dimensional algorithm equivalent to a modified version of the weak con- straint 4D-VAR algorithm was developed and applied in the context of a quasi-geostrophic two-layer ocean model. This included the development of the forwards and adjoint models as well as error visualisation tech- niques.
This concluding chapter reviews the content of the thesis as a whole, summarizes the response to the key ques- tions posed in Chapter 1, discusses the potential for the application of these results in operational ocean fore-
casting and finishes with an enumeration of possible directions for future work.
![]()
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1678
ISSN 2229-5518
We wish to thank our departmetnfor allowing us to do this extensive work and finally conclude the thesis, also my family and friends.
• S. Akella and I. M. Navon. A compara- tive study of high resolution advection schemes in the context of data assimila- tion. International Journal for Numer- ical Methods in Fluids, 51:719–748,
2006.
• A. Arakawa and V. R. Lamb. A poten- tial enstrophy and energy conserving scheme for the shallow water equa- tions. Monthly Weather Review,
109:18–36, January 1981.
• A. Arakawa and V. R. Lamb. Computa- tional design of the basic dynamical pro- cesses of the UCLA general circulation model. Methods in Computational Physics, 17: 173–265, 1977.
• N. Ayoub. Estimation of boundary val- ues in a North Atlantic circulation model using an adjoint method. Ocean Modelling, 12(3–4):319–347, 2006.
• I. J. Barton. Satellite-derived sea sur- face temperatures: Current status. Journal of Geophysical Research,
100(C5) :8777–8790, May 1995.
• G. K. Batchelor. An Introduction to Fluid Dynamics. Cambridge Universi- ty Press, 1967.
• M. J. Bell. Momentum fluxes in the Bryan/Cox ocean circulation model. Journal of Atmospheric and Oceanic Technology, 15(6):1400–1413, De- cember 1998.
• J.-D. Benamou and Y. Brenier. A Computational Fluid Mechanics solu-
tion to the Monge-Kantorovich mass
transfer problem. Numerische Mathe- matik, 84(3) :375– 393, 2001.
• J.-D. Benamou, Y. Brenier, and K.
Guittet. The Monge-Kantorovitch mass transfer and its Computational Fluid Mechanics formulation. International Journal of Numerical Methods in Flu- ids, 40(1–2) :21–30, 2000.
• A. F. Bennett. Inverse Methods in Physical Oceanography. Cambridge University Press, Cambridge, UK,
1992.
• C. W. B¨oning, W. R. Holland, F. O.
Bryan, G. Danabasoglu, and J. C. McWilliams. An overlooked problem in model simulations of the thermohaline circulation and heat transport in the At- lantic Ocean. Journal of Climate,
8:515–523, 1995.
• Y. Brenier. Polar factorization and monotone rearrangement of vector- valued functions. Communications on Pure and Applied Mathematics, 44(4)
:375–483, June 1991.
• Y. Brenier and W. Gangbo. LP approx- imation of maps by diffeomorphisms. Calculus of Variations, 16:147–164,
2003.
• K. A. Brewster. Phase-correcting data assimilation and application to storm- scale Numerical Weather Prediction. Part i: Method description and simula- tion testing. Monthly Weather Review,
13 1:480–492, 2002a.
• K. A. Brewster. Phase-correcting data assimilation and application to storm- scale Numerical Weather Prediction. Part II: Application to a severe storm outbreak. Monthly Weather Review, 13
1:493–507, 2002b.
• K. Bryan. A numerical investigation of a nonlinear model of a wind-driven
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 1679
ISSN 2229-5518
ocean gyre. Journal of the Atmospheric
Sciences, 594:594–606, 1963.
• Buizza and T. N. Palmer. The singular- vector structure of the atmospheric global circulation. Journal of Atmos- pheric Science, 52(9):1434–1456, May
1995.
• J. G. Charney, R. G. Feagle, H. Riehl, V.
E. Lally, and D. Q. Wark. The feasibility of a global observation and analysis ex- periment. Bulletin of the American Me- teorological Society, 47:200–220,
1966.
• E. Cohn, N. S. Sivakumaran, and R.
Todling. A fixed-lag kalman smoother for retrospective data assimilation.
Monthly Weather Review,
122(12):2838–2867, December 1994.
IJSER © 2014 http://www.ijser.org