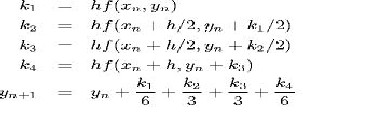International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 603

ISSN 2229-5518

Mathematical Modelling of

Temperature Rise in Clutch and Design, Analysis and Fabrication of Cooling System for Clutch

1Rahul R, 2Pugazhenthi R, 3Eugene Jesu Antony A, 4Viswanath B and 5Asst Prof. Arul Selvan S

1Department of Automobile Engineering, Anna University, Madras Institute of Technology Campus, India rahulmitautomobile.39@gmail.com

2Department of Automobile Engineering, Anna University, Madras Institute of Technology Campus, India

pugazh464@gmail.com

3Department of Automobile Engineering, Anna University, Madras Institute of Technology Campus, India uginanton y@gmail.com

4Department of Automobile Engineering, Anna University, Madras Institute of Technology Campus, India

viswa481@gmail.com

5Department of Automobile Engineering, Anna University, Madras Institute of Technology Campus, India arul@annauniv.edu

Abstract—The temperature rise in a motorcycle wet multi-plate clutch during engagement and disengagement is very crucial because it is one of the parameters which have a direct influence on the clutch life. The slipping of the clutch happens during engagement and disengagement where the friction material on the plates will undergo a change of state from solid to semi-solid state and the friction material properties start to deteriorate. In order to optimise the clutch life it is very important to identify the parameters affecting temperature rise. The temperature measurement setup was developed during the Internship program. Mathematical modelling would help in developing the equation for predicting the temperature rise. The project involves combining equations of different physical phenomena like heat conduction in the plates, convective heat transfer by the lubrication oil, torque transfer by the clutch and energy balance equations. Mathematical modeling using ordinary differential equation was determined to calculate the temperature rise. The mathematical model was analyzed using MATLAB and graphs were generated. The generated graphs were compared and validated by the experimental results obtained from Internship program. The cooling system of clutch was designed, analysed and fabricated by providing cooling fins to the existing clutch cover for improving the cooling for the existing system.

Keywords: Temperature Rise, W et Multiplate Clutch, Mathematical Modelling, Design, Matlab Analysis

—————————— ——————————

1 INTRODUCTION

The temperature rise in a motorcycle wet multi-plate clutch during engagement and disengagement is very crucial because it is one of the parameters which have a direct influence on the clutch life. The slipping of the clutch happens during engagement and disengagement where the friction material on the plates will undergo a change of state from solid to semi-solid state and the friction material properties start to deteriorate. In order to optimize the clutch life it is very important to identify the parameters affecting temperature rise.
Mathematical modeling would help in developing the equation for predicting the temperature rise. The project involves combining equations of different physical phenomena like heat conduction in the plates, convective heat transfer by the lubrication oil, torque transfer by the clutch and energy balance equations. Mathematical modeling using ordinary differential equation was determined to calculate the temperature rise.
The mathematical model was analyzed using MATLAB and graphs were generated. The generated graphs were compared and validated by the experimental results obtained from Internship program. The cooling system of clutch was

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 604

ISSN 2229-5518

designed, analysed and fabricated by providing cooling fins to the existing clutch cover for improving the cooling for the existing system.
The main purpose of the project is to develop a mathematical model of temperature rise in the wet multi-plate clutch and experimentally validate it. The second part of the project involves design, analysis and fabrication of cooling system for clutch by providing external cooling fins on the clutch cover. The major part of the first part of project is theory oriented. MATLAB software is used for solving the ordinary differential equation obtained using Runge Kutta method. The graphs are generated using MATLAB software and are experimentally validated. The second part of the project involves is both theory and practical oriented.

2 EXPERIMENTAL SET-UP AND PRE-REQUIREMENTS

2.1 LITERATURE REVIEW

The following are the parts of the wet multi-plate clutch system of a motorcycle. The various parts used in a wet multi-plate clutch system are showed in Figure1:
• Clutch disc
• Friction disc
• Clutch hub
• Pressure plate
• Bearing
• Clutch springs

Figure 1
The following literature review describes important research results obtained from various research papers.
During the engagement of wet clutches, large amount of friction heat is generated at the separator- friction lining interface in a short time. This results in a non-uniform temperature increase in clutch
components, especially in the friction lining. There is a temperature gradient from the surface to the interior of the friction disc lining material. The surface temperature of the wet friction materials is especially important because it controls the performance characteristics such as friction properties, rate of wear, and transmission oil decomposition. Furthermore, the non-uniform temperature distribution within the friction materials will cause thermal stress to occur. [1]
The oil environment of a wet clutch provides the potential for smooth engagement and long life as well as the possibility of convective cooling of the clutch either by natural or forced convection of the lubrication oil. [2]
Heat is generated in clutches as a result of slippage that occurs as the clutch engages while transmitting torque. Although slippage is nescessary to provide for smooth starts and on the- go shifts, excessive temperatures can cause damage to the transmission oil and the transmission components, especially the friction material on the friction plates. [3]
An energy balance in a slipping clutch can be stated as the “power dissipated in the clutch equals the net rate of heat rejected from the clutch plus the rate of heat storage in the clutch. [4]
Pdis = Qrej + Qstored
An accurate clutch torque control is required, which necessitates a good knowledge of clutch friction characteristics. The friction characteristics are generally influenced by fluid type, friction lining material including surface roughness; clutch slip speed, applied force, friction interface temperature, and friction lining wear. In the fields of Automatic transmission research, where paper-based friction lining material is mostly used, the friction characteristics are commonly characterized. [5]
Description of the wet clutch thermal dynamics is, generally, a complex time-varying spatially- distributed problem. It is based on heat balance laws for the clutch components (separator plate, friction lining, and core plate) and a choice of appropriate boundary conditions. The solution can be obtained by time consuming finite element or finite difference methods. Such an approach gives a good insight into temperature distribution in the whole clutch pack, and can be effectively utilized for optimization of the clutch components design and the choice of materials. However, this approach is not suitable for on-line temperature estimation due to model complexity, memory requirements, and computing inefficiency. Therefore, there exists a need for simple

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 605

ISSN 2229-5518

thermal models that can be easily experimentally parameterized and eventually provide acceptable modelling accuracy. [6]

2.2 MATHEMATICAL MODELLING BASICS

Since prehistorical times simple models such as maps and diagrams have been used. Often when engineers analyze a system to be controlled or optimized, they use a mathematical model. In analysis, engineers can build a descriptive model of the system as a hypothesis of how the system could work, or try to estimate how an unforeseeable event could affect the system. Similarly, in control of a system, engineers can try out different control approaches in simulations.
A mathematical model usually describes a system by a set of variables and a set of equations that establish relationships between the variables. The variables represent some properties of the system, for example, measured system outputs often in the form of signals, timing data, counters, and event occurrence (yes/no). The actual model is the set of functions that describe the relations between the different variables. [7]
A mathematical model usually describes a system by a set of variables and a set of equations that establish relationships between the variables shown in figure
2.

Figure 2

2.3 MATLAB STUDY

MATLAB is a high-performance language for technical computing. It integrates computation, visualization, and programming in an easy-to- use environment where problems and solutions are expressed in familiar mathematical notation. MATLAB is a high-performance language for technical computing. It integrates computation, visualization, and programming in an easy-to-use environment where problems and solutions are expressed in familiar mathematical notation. Typical uses include:
• Math and computation
• Algorithm development
• Modeling, simulation, and prototyping
• Data analysis, exploration, and visualization
• Scientific and engineering graphics
• Application development, including
Graphical
• User Interface building
MATLAB is an interactive system whose basic data element is an array that does not require dimensioning. This allows you to solve many technical computing problems, especially those with matrix and vector formulations, in a fraction of the time it would take to write a program in a scalar non interactive language such as C or Fortran.
The name MATLAB stands for matrix laboratory. MATLAB was originally written to provide easy access to matrix software developed by the LINPACK and EISPACK projects, which together represent the state-of-the-art in software for matrix computation.
MATLAB has evolved over a period of years with input from many users. In university environments, it is the standard instructional tool for introductory and advanced courses in mathematics, engineering, and science. In industry, MATLAB is the tool of choice for high-productivity research, development, and analysis.
MATLAB features a family of application-specific
solutions called toolboxes. Very important to most users of MATLAB, toolboxes allow you to learn and apply specialized technology. Toolboxes are comprehensive collections of MATLAB functions (M-files) that extend the MATLAB environment to solve particular classes of problems. Areas in which toolboxes are available include signal processing, control systems, neural networks, fuzzy logic, wavelets, simulation, and many others. [8]
MATLAB is an indispensable asset for scientists, researchers, and engineers. The richness of the MATLAB computational environment combined with an integrated development environment and straightforward interface, toolkits, and simulation and modelling capabilities, creates a research and development tool that has no equal. From quick code prototyping to full blown deployable applications, MATLAB stands as a de facto development language and environment serving the technical needs of a wide range of users. [9]

3 MATHEMATICAL MODELLING FOR TEMPERATURE RISE IN CLUTCH

Energy balance equation of a clutch

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 606

ISSN 2229-5518

Pdis = Qrej + Qstored -> 1
The rejected heat is mainly due to the presence of cooling oil.
Qrej =m Coil (Toil out – Toil in ) ->2
Where,
Coil – Specific heat capacity of oil
Toil out – Temperature of the oil leaving the clutch
Toil in – Temperature of the oil entering the clutch
The change in temperature of the oil is due to convective heat transfer from the plates due to friction.
If the plate temperature is considered to be uniform i.e. no hotspots are considered. [Assumption from a paper – “Computer modelling of the heat transfer in a powershift transmission clutch under slippage” – Kansas State University]
Qrej = h A ( Tplate - Toil ) ->3
Toil is the mean temperature of the oil [Around 110 deg C – obtained from experimental results]
The heat energy stored in the system is completely stored in the clutch plates.
Ordinary differential equation model for coefficient of convective heat transfer and temperature rise was determined using basic thermodynamic principles. Heat transfer differential equations for wet multi- plate clutch were identified. The equation 6 is modeled and analyzed using the MATLAB software to get the appropriate graphs required to understand the parameters affecting the clutch temperature rise. The Ordinary differential equation obtained is solved by the Numerical method approach called as Runge Kutta method.

4.1 RUNGE KUTTA METHOD

In numerical analysis, the Runge–Kutta methods are an important family of implicit and explicit iterative methods, which are used in temporal discretization for the approximation of solutions of ordinary differential equations.
Qstored= m plate Cplate

𝑑𝑇

𝑑𝑡

-> 4

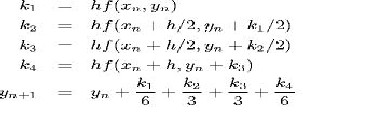
4.2 MATLAB CODING

𝑑𝑇

𝑑𝑡

is the temperature rise in the clutch plate with
respect to slip time
A differential term is involved because only the plate’s temperature increases with respect to slipping.
Pdis = h A ( Tplate - Toil ) + m plate Cplate
Equation 5 when solved gives:

𝑑𝑇

𝑑𝑡

->5
Figure 3

𝑑𝑇

𝑑𝑡 = [Pdis - h A ( Tplate - Toil )] / ( m plate Cplate ) ->6

The above equation can be solved using MATLAB to
generate respective graphs and the obtained graphs
can be compared with the experimental results for validation.

4 MATLAB ANALYSIS AND GRAPH GENERATIONS

Figure 4

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 607

ISSN 2229-5518

150

Toil

MATLAB Graph

100

Figure 5
The above code has been generated using the MATLAB software shown in figure 3, figure 4 and figure 5. The obtained ordinary differential equation is solved using the Runge Kutta fourth order method. The Runge Kutta method is chosen because it is the most accurate method for solving first order ordinary differential equations.

4.3 MATLAB GRAPHS

The following graphs were generated by solving the ordinary differential equation of the obtained mathematical model using Rungekutta method by MATLAB software. Three graphs have been generated and the parameters have been mentioned in the respective axes.

0 20 40 60

Iteration

Figure 7

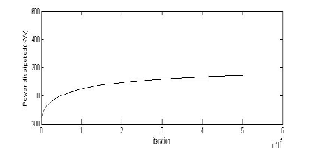
Figure 7 shows the temperature change of oil with respect to the number of iterations obtained by solving the mathematical model using Runge Kutta method.

300

200

100

Tplate

MATLAB GRAPH

0 10 20 30

Iteration

Figure 8
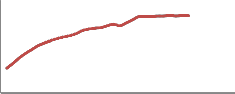
Figure 8 shows the power dissipation with respect to the number of iterations obtained by solving the mathematical model using Runge Kutta method. The power dissipation increases with respect to the number of iterations because power transmitted through the clutch is lost when the temperature in the clutch plate increases.

5 DESIGN OF COOLING SYSTEM

Figure 6
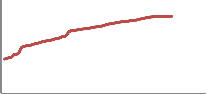
Figure 6 shows the temperature change of clutch plate with respect to the number of iterations obtained by solving the mathematical model using Runge Kutta method.
The existing clutch cover in a motorcycle is not provided with cooling fins. If cooling fins are added to the existing clutch cover it would enhance the cooling of the clutch oil by significant manner. The enhancement of the clutch cover to provide better cooling design is shown below. As the clutch oil is cooled by a significant manner the clutch is also cooled to a better extent than the existing cooling system. Thereby clutch life can be increased.

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 608

ISSN 2229-5518

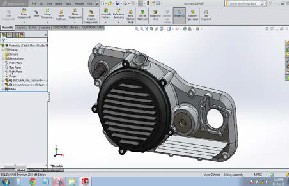
SolidWorks software was adopted to design the enhanced cooling system. The specifications of the provided cooling fins are as follows.
• Material: Aluminum alloy
• Thickness: 4mm
• Width: 40 mm
The above specifications were chosen by consulting the available material in the market and by analysing if it is suitable for TIG Welding. Later the above section was analysed and checked if it enhanced the cooling by a significant manner.

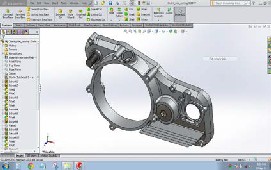
Figure9
Figure 9 shows the exploded view of the main part of the clutch cover with additional cooling fins.

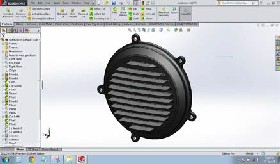
Figure 10
Figure 10 shows the exploded view of the outside part of the clutch cover with additional cooling fins.
Figure 11
Figure 11 shows the assembled view of the clutch cover where the design change has been carried out by the addition of cooling fins. The cooling fins were added in order to improve cooling of the clutch oil present inside the clutch cover.

5.1 ANALYSIS OF THE COOLING SYSTEM

The above chosen section was analyzed using SOLID Works software by providing air flow simulation.
The boundary conditions are chosen as below:
• Air flow speed: 90kmph
• Temperature on the surface of the clutch cover: 80°C

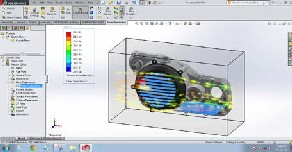
Figure 12
Figure 12 shows the air flow simulation of the cooling fins added to the clutch cover. The maximum heat convection by air flow was observed in the area indicated by red colour. The change in colour from yellow to green or red depicts the heat convection by air flow.

6 FABRICATION OF COOLING SYSTEM

6.1 CLUTCH COVER MARKING

The clutch cover was procured from the Genuine parts and it was modified to meet the requirements

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 609

ISSN 2229-5518

of the project. In order to fabricate the enhanced cooling system the first step is to locate the places in which the cooling fins have to be attached as shown in figure 13. The locations were obtained by analysis and air flow simulation from Solidworks software and accordingly the locations for cooling fins were chosen. A permanent marker was used to carry out the marking to make the TIG welding process easier.

Figure 13

6.2 METAL CUTTING FOR FINS

The required dimensions for the cooling fins were obtained from the design and analysis using Solidworks software. The required dimensions need to be cut in order to be used as cooling fins for the existing cluth cover system as shown in figure 14.

Figure 14

6.3 SURFACE GRINDING OF CLUTCH COVER

In order to carry out the TIG welding process the paint on the existing clutch cover system needs to be scrapped off so that the welding process can become easier. Hand held surface grinding machine was used to carry out the surface grinding process. The figure 15 shows the ground surface of the existing clutch cover.

Figure 15

6.4 TIG WELDING - ALUMINIUM

Gas tungsten arc welding (GTAW), also known as tungsten inert gas (TIG) welding, is an arc welding process that uses a non-consumable tungsten electrode to produce the weld. The figure
16 and 17 show the aluminium welded parts to the
clutch cover. Figure 17 shows the enhanced cooling system.

Figure 16

Figure 17

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 610

ISSN 2229-5518

6.5 COOLING OF THE WELDED FINS

The TIG Welding process for Aluminium welding will induce extreme thermal stresses to the components welded. This heat energy exerted to the components will definitely rise the temperature of the enhanced clutch cover. Therefore the welded components need to be cooled. The fabricated cooling system is dipped in cooling oil and also sprayed with distilled water so that the heat is released and temperature reduces. This marks the end of the fabrication part of the project. At the end the fabricated part looks like the figure 17 shown above. This part can be implemented in vehicles for enhanced cooling of the clutch oil.

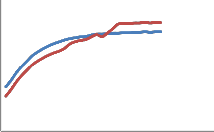
Tplate

Experimental Graph MATLAB GRAPH

300

250

200

150

100

7 RESULTS AND DISCUSSIONS

7.1 VALIDATION OF MATHEMATICAL MODEL

The graphs generated from the MATLAB SOFTWARE were compared to the experimental graphs and validation was carried out. It was observed that the Temperature of oil graph had very similar results for both the mathematical model and experimental results. So the mathematical model developed by Runge Kutta method had very similar results to the experimental data obtained. The model is thus validated as said above. It was also observed that only a few parameters taken in the mathematical model could be controlled to reduce the temperature rise. It was deducted that controlling the temperature of oil had significant reduction in the temperature of the plate. That is the reason why the later part of the project was focussed on reducing the temperature of the oil to a considerable extent thereby reducing the temperature of the plate. As the temperature of the plate during slip is reduced the clutch life will improve.
Figure 24 shows the validation of the temperature of the plate curve obtained using the mathematical model. The temperature of the plate graph obtained from the mathematical model had slight deviation from the graph obtained from the experimental results because of some data approximation carried out in mathematical model analysis. Though there was slight deviation, the trends of the graphs were similar.

0 10 20 30 40

Cycle (or) Iteration

Figure 24

Toil

Experimental Graph MATLAB Graph

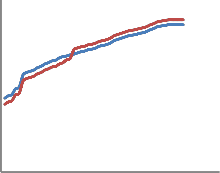
140

120

100

0 20 40 60

Cycle (or) Iteration

Figure 25
Figure 25 shows the validation of the temperature of the oil graph obtained using the mathematical model. The MATLAB graphs and experimental graphs showed very slight deviation. This is because of the data approximation carried out in the MATLAB analysis of the mathematical model.

8 CONCLUSION

A mathematical model was developed for the temperature rise in a wet multi-plate clutch and graphs were generated. Experimental validation was carried out and graphs were also generated from the experiments. The graphs of the mathematical model

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 611

ISSN 2229-5518

as well as the experimental results were compared in order for validation purpose. It was seen that the both the experimental and MATLAB generated graphs followed similar trends. Thus the mathematical model was validated. Enhanced cooling system for clutch was designed, analysed and fabricated. The simulation results from the enhanced cooling system proved a reduction in the temperature of the surface of the cover clutch thus enhancing the cooling for cooling oil.
The Results are as follows:
• The mathematical model for temperature rise was developed.
• The mathematical model developed was an
Ordinary differential equation.
• The model was solved by the Runge Kutta fourth order method using the MATLAB software.
Graphs were generated comparing the temperature of plate and temperature of oil against the number of iterations.
• The parameter to be controlled was chosen as the temperature of oil in order to reduce the temperature of the plate.
• The obtained mathematical model was validated by experimental results obtained from the Internship program carried out by one of the members in our group.
• Enhanced cooling system to reduce the temperature of the oil was designed, analysed using Solid works software.
• Air flow analysis was done in order to validate the design of the enhanced cooling system.
• The enhanced cooling system was fabricated by carrying out processes like metal cutting, surface grinding and Aluminium TIG welding.

9 REFERENCES

[1] Hiroshi Yabe, Yubo Yang, Robert C. Lam and Yih Fang Chen“Modeling of Heat Transfer and Fluid Hydrodynamics for a Multidisc Wet Clutch” SAE Series

950898

[2] David A Pacey and Ralph 0 Turnquist. “Modeling Heat

Transfer in a Wet Clutch” SAE Series 901655

[3] David A Pacey and Ralph 0 Turnquist. “Modeling Heat

Transfer in a Wet Clutch” SAE Series 901655

[4] Johnson P W."ComputerModeling of the Heat Transfer in a Powershift Transmission Clutch under Slippage," Master of Science Thesis, Mechanical Engineering, Kansas StateUniversity.

[5] Vladimir Ivanović, ZvonkoHerold and JoškoDeur.”

Experimental Characterization of Wet Clutch Friction

Behaviors Including Thermal Dynamics” SAE Series 2009-

01-1360

[6] Vladimir Ivanović, ZvonkoHerold and JoškoDeur.” Experimental Characterization of Wet Clutch Friction Behaviors Including Thermal Dynamics” SAE Series 2009-

01-1360

[7] Schade C.W. “Effects of transmission fluid on clutch performance” SAE Series 710734

[8]http://www.cimss.ssec.wisc.edu
[9]http://www.intechopen.com