International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1620
Introduction to Communications Systems
Prepared By:
Hassan Natto
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1621
IntroducCon . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Lossless Data Compression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Lossless vs. Lossy Data Compression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Lossless Data Compression Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
StaCsCcal Modeling (Class I) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
Burrows-‐Wheeler Transform (BWT) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
LZ77 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
LZW . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
PPM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Bit String (Class II) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Huffman Coding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
ArithmeCc Coding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Huffman Coding vs. ArithmeCc Coding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Performance Comparison: Uncompressed vs. Compressed . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
So7ware Part . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Reference: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Appendix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1622
Introduction
Today most of the communications are done through digital systems. Digital systems offer high quality and good performance. Good performance can only be achieved when the retrieved received information is exactly the same as the originally sent information. When the information is sent there is a good chance that the information gets corrupted and sometimes the numbers of errors are increased so much that the main information is lost. Therefore different techniques are used to minimize the effects of error so that high percentage of the information can be retrieved at the receiver end. One of such techniques is known as data compression. In data compression the data bits are compressed in order to minimize the size of the sequence. Compressing the data makes easier to store more data when compared with the uncompressed data. Also the compresses data is transferred faster as there are fewer amounts of bits than original. There are two main classes of the data compressions, lossy data compression and lossless data compression.
In this paper lossless data compression will be discussed in detail. First an overview will be given about lossless data compression and then its difference when compared to the lossy data compression. After the algorithms used for the lossless data compression will be discussed and at the end one of the algorithms will be implemented in the Matlab
and the results will be discussed.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1623
Data compression techniques are used at the source end where the data is ready to be sent. Lossless data compression is also performed at the source end and is used during the source encoding. In lossless data compression algorithms the received data is retrieved exactly like the original data. Thus, lossless data compression algorithms help in retrieving the original data and also make the transfer fast by minimizing the size of the information.
In lossless data compression algorithms first the redundant information is removed from the data and then the data is compressed at the source end. At the receiver end the same data is reconstructed again by restoring the redundant information. With this technique the replica of the original data can be retrieved at the receiver end. There are many applications of the lossless data compression algorithms but the most popular is the zip file format. Besides this the most important use of the lossless data compression algorithms is when transferring the sensitive information. For example, when there is a need to receive the information without any errors then in such cases the lossless data compression algorithms are used because with their help the received information can be retrieved exactly like the original data. These could include executable source codes, images etc., because if executable source codes got corrupted then the outcome will be different. Therefore, lossless data compression algorithms provide better and fast performance as the size of the original data becomes small and also can be retrieved in
the exact original form. [1]
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1624
In the lossy data compression, the data is compressed by using some of the redundant bits. This means that if the redundant bits get corrupted then it will make it difficult to retrieve the original data. There are certain differences between lossless and lossy data compression algorithms. These differences are as follows:
a) The first and the most important difference is that the lossless data compression provides more accuracy in the data retrieval whereas with lossy data compression there is a chance that the retrieved data is not exactly the same as the original data.
b) For lossless data compression, the data retrieved is not much different to the original data at the bits level but in the case of lossy data compression the retrieved data at the bits level can be completely different which can’t be recognizable by human ears or eyes.
c) Lossless data compression mostly works on statistical redundancy. For example, the alphabets like ‘a’, ‘d’ are most commonly used than ‘z’, therefore based on such statistics the data is compressed. Lossy data compression doesn’t follow statistical redundancy.
d) For high compression lossy data compression allows to neglect some of the information. That information is excluded during the compression and the user
will not be able to see or hear it, whereas, lossless data compression doesn’t
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1625
allow any exclusion of the data and all the retrieved data is exactly the same as the original data. In such cases where high compression is required the lossless data compression will fail as it will not allow any exclusion of the data whereas in such cases lossy data compression will be a good choice. [2]
As discussed before lossless data compression algorithms can be applied to many applications like, text, images, sound files, video files etc. Therefore, there are different algorithms for different applications. These algorithms are based on two main classes, one deal with the statistical modeling and other with bit strings. Therefore for each class the algorithms are different.
Statistical Modeling ( Class I )
In statistical modeling the compression is based on statistical redundancy. The algorithms used in this class are, Burrows-Wheeler Transform, LZ77, LZW and PPM.
Burrows-Wheeler Transform (BWT)
This algorithm is not used to compress the data rather it is used to transform the data into simple form so that it could be properly compressed. In BWT some information is added to the original data so that it that information could be helpful in retrieving the data correctly. The main advantage of BWT is that in other algorithms it becomes a complex process to compress the very long string of information because it will take
more time and resources in doing that, but with BWT it becomes simple and fast
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1626
because it add some information to the original information which makes the information simple to compress. [3]
LZ77
In LZ77 or Deflate algorithm, the data is compressed depending how many characters are repeated. To keep track of the characters a ‘sliding window’ is used. Sliding window keeps the record of all the repeated characters. When a new sequence of characters are required to be compressed the sliding window check how many characters from the present sequence had been repeated previously. If there is a repeating character in the sequence the LZ77 performs two actions. First, the distance, how far was the previous repeated character in the sliding window. Second, the length, the number of characters that the repeated in a sequence. The disadvantage of this algorithm is that it could be quite time consuming because for larger sequence of information more characters are to be matched and this could take time. [4]
LZW
Lempel-Ziv-Welch (LZW) is a dictionary based algorithm which deals with the repeating data. The number of time the data is repeated a specific reference is given to it which could be different from other repeating data or characters. Therefore for every repeating data a unique reference is set which later is used in place of the repeating data. Like LZ77, LZW also uses sliding window that keep tracks of all the repeating characters or a data. The application of the LZW algorithm is for PDF files, GIF files etc. There are many advantages of the LZW algorithm. First it works better for large
repetitive data because with more repetitive data more unique references can be assigned
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1627
and this will make the data sequence more secured and compressed. LZW compression is fast as with more repetitive data it will be easier to compress the data more quickly. Beside these advantages there are certain disadvantages of LZW algorithm. Firstly, for a large data sequence if there are less number of characters that are repetitive then it will take more time to compress the data and also the size of the data could be increased. Therefore to compress the data it is important that many characters should repeat in the data sequence. Another disadvantage is that, it is an old technique. Today computers are able to utilize even complex algorithms in short time. So such algorithms sometimes are considered to be more useful than LZW algorithm. [4]
PPM
Partial Pattern Matching (PPM) algorithm compresses the information on the symbol level. A symbol wise model is used that generates the statistics of the data based on the symbol information. All this process keeps on going until there is no more data to be compressed. On these bases a conditional probability is assigned to each symbol in the data sequence. One of the advantages of PPM is that is doesn’t only follow a fixed-order context. This means that it could switch from lower to higher order and vice versa. This switching is done through blending scheme. Another advantage is that PPM algorithm tries to predict the next character based on the probability. The character with highest probability is most likely to be the next one and therefore with the prediction of the next characters the information sequence becomes more predictable and can be compressed
efficiently. [3]
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1628
Bit String ( Class II )
In this class the data is compressed based on the bits. In previous discussed algorithms the data was compressed based on the characters repetition. But in this class, algorithms work with the bit sequence. The two main algorithms used are Huffman coding and arithmetic coding.
Huffman Coding
The Huffman coding deals with assigning short code words to every input data blocks, the assigning of such code words is based on the probability of each character. The symbols are the used frequently are assigned with the short code word and those that are less frequently repeated are assigned with higher code words. Thus for each block the length of the assigned code words varies. The main focus of Huffman coding is to use the frequency of the characters in order to compress the data. Huffman algorithm is also known as a greedy algorithm because it always chooses the best choice present at the moment, makes optimal choices so that at the end those choices lead to the right solution and once the algorithm makes the choice the decision remains the same till the end.
Huffman coding is very fast and can compress the data more than other algorithms. When the numbers of repetitive character are quite high then at some situation the Huffman algorithm can give a compression rate up to 80%. The main application of
Huffman algorithm is in ZIP file format, Jpegs and Mpegs. [3]
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1629
Arithmetic Coding
Like Huffman coding, arithmetic coding also use probabilities of the characters and assign the data sequence a code word. But the main advantage of arithmetic coding is that is gives an ideal length of the code words to the data sequence, unlike Huffman code where variable lengths of code words are assigned based on the probability ratio. Therefore with ideal length the data compression becomes fast and it will become easier to compress large sequences.
Both the Huffman and arithmetic coding works with the probabilities that how many times a character is repeated. But the difference is when the code words are assigned to the symbols. Huffman coding assigns variable lengths of the code words based on the probability whereas the arithmetic coding gives the same length of the code words.
Arithmetic coding efficiency is always equal or better than the Huffman coding because it is able to compress more data than Huffman. Furthermore because of assigning multiple bits to the characters Huffman coding can show some rounding errors but these errors are minimized, while using arithmetic coding.
With the implementation of the arithmetic coding the compression rate can be increased further to 5% to 10% when compared with the Huffman coding compression rate. Therefore arithmetic coding provides better performance than Huffman coding for any
length of data sequence. [3]
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1630
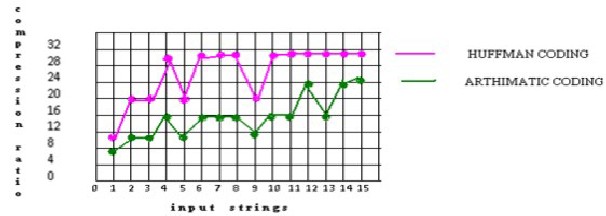
To analyze the performance of the Huffman and arithmetic coding, it is important to consider the compression ratio of both the coding schemes. Below figure shows a good comparison of compression ratios for Huffman and arithmetic coding.
Figure: 1. Comparison of Compressed Ratio of Huffman and Arithmetic Coding
From the graph it can be seen that the arithmetic coding provides much better results than the Huffman coding. The figure shows the comparison of compressed ratio for the inputs strings. It can be seen that for 15 input strings the compressed ratio of Huffman coding is 28% whereas that of arithmetic coding is 21%. This means that the arithmetic coding helps in reducing the size of the string much better than the Huffman coding. This also can be analyzed that for large input strings the arithmetic coding provides better performance than Huffman coding. Therefore for much large data sequence it is better to implement arithmetic coding than Huffman coding. Furthermore arithmetic coding performance much better in reducing the channel bandwidth and transmission time whereas Huffman coding takes more time for the data to be transmitted. [5]
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1631
Below graph shows the comparison of uncompressed data and how much it can be compressed by applying different algorithms. It can be seen that the size of the file is
1200kB uncompressed but when the compression algorithms are applied the file size reduced to 95kB. The best compression rate is given by the prediction pattern matching. [6]
Figure: 2. 32-bit file: Comparison between the compression rates of different algorithms
The next graphs shows the performance comparison regarding how much time different compression algorithms take to compress the data. From the graph it can be seen that the Huffman coding takes less time than other algorithms while doing compression. It can be seen that Huffman performance is much better than LZW and RLE. [2]
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1632

Figure 3: Compression rate in Time
The Huffman code is presented in the Appendix. The program is written in Matlab. The program is developed for the input sequence 1-6 and with unknown probabilities. The program will first calculate the probabilities of each input and then the resulting Huffman codes words in bits will be generated. The program shows the code words of each input.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1633
Today data compression becomes really important because it extra bandwidth becomes available to transmit more data, also the transmission rate decreases this make the communication fast and effective. Data compression is done at the source end and decompressed at the receiver end. There are different methods to compress the data but the two main methods are lossy data compression and lossless data compression. The main difference is that the with the lossless data compression it is possible to retrieve the data exactly like the original data whereas with lossy data compression sometime it is not possible to retrieve the replica of the original data. Therefore in many applications lossless data compression techniques are used.
There are different techniques used in the lossless data compression and these techniques are differentiated based on the statistical modeling and bit strings. Statistical modeling algorithms include BWT, LZ77, LZW and PPM. These algorithms deal with the repetitive characters. This means that for the repetitive characters different unique references are assigned. The algorithms using bit strings works at the bit level. The most popular algorithms are Huffman and arithmetic coding. Huffman and arithmetic coding deals with the probabilities of the characters and can predict what will be the next character. In most application Huffman coding is implemented because it is fast and easy to use whereas arithmetic coding is less frequently used but provides better
performance than Huffman coding in terms of channel bandwidth and transmission time.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1634
[1] CCSDS. (2006). “Lossless Data Compression,” Informational Report.
Available at: http://public.ccsds.org/publications/archive/120x0g2.pdf
[2] Rui del-Negro. (2011). “Data Compression Basics,” Available at:
http://dvd-hq.info/data_compression_1.php#Comparison
[3] Khalid S. (2003). “Lossless Compression Handbook,” Elsevier Science
(USA)
[4] Wallace W. (2008). “Beginning Programming for Dummies,” Wiley
Publishing, Inc., Indiana
[5] O. Srinivasa Rao, S. Pallam Setty. (2011). “Comparative Study of Arithmetic & Huffman Data Compression Techniques for Koblitz Curve Cryptography,” International Journal of Computer Applications, vol. 14(5). Available at:
http://www.ijcaonline.org/volume14/number5/pxc3872346.pdf
[6] S.R. Kodituwakku, U.S. Amarasinghe. “Comparison of Lossless Data Compression Algorithms for Text Data,” Indian Journal of Computer Science & Engineering, vol. 1(4). Available at:
http://www.ijcse.com/docs/IJCSE10-01-04-23.pdf
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014
ISSN 2229-5518
1635
close all;
clc;
clear all;
%------------------------------------------------------------------------------%
% This program generates a Huffman codes for each input based on the unknown
% probability model. huffmandict geneterates the huffman code for each
% input
%------------------------------------------------------------------------------%
input_sequence = [1:6]; % input sequence for which huffman algorithm is used
prob=input_sequence(:)/sum(input_sequence); % Probabilites for each input. The sum of probabilities must be 1
[dict,average_len] = huffmandict(input_sequence,prob); %Generates a binary Huffman code using the maximum variance algorithm.
for i = 1:length(input_sequence)
codeword = dict {i,2}; %Codeword for each signal value disp(codeword) %Codewords output
end
IJSER © 2014 http://www.ijser.org