International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1365

ISSN 2229-5518

How to Prepare Input File of Reservoir Simulation by Using Reservoir Characterization

Habibu Shuaibu 1 and Attia M. Attia 2

ABSTRACT- The most generally encountered and certainly the most challenging responsibility in reservoir engineering is the description of a reservoir, both accurately and efficiently. Most of enhanced oil recovery and secondary recovery projects fails due to inadequate and insufficient reservoir characterization and dealing with heterogonous reservoir. An accurate description of a reservoir is crucial to the management of production and efficiency of oil recovery. Reservoir characterization plays a very important role in descripting the storage and flow capacity of a reservoir and also plays a decisive role in reservoir simulation. The main objective of this research is on how to prepare a reservoir simulation input file accurately to receive an accurate output, in other to achieve this we most follow the following steps. Firstly by identifying the degree heterogeneity by using methods such as Lorenz Coefficient and Dykstra-Parsons coefficient , secondly by using existing and recognised techniques such as FZI or HFU, permeability group, DRT to estimate the different flow units and then classifying reservoir rocks (rock typing) in a petrophysical reliable manner using approaches such as RQI, FZI, DRT, winland R35 method and allocating properties to each rock type which will aid in estimating permeability for uncored wells. Finally in order to enhance the accuracy, a comprehensive analysis and comparison of all techniques is evaluated to predict the most accurate and more reliable method to be applied to any reservoir.

Index Terms: Flow Zone Indicator (FZI), Reservoir Quality Index (RQI), Hydraulic Flow Unit (HFU), Discrete Rock Typing

(DRT), W inland (R35).

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1366

ISSN 2229-5518

Introduction

Reservoir characterization plays a vital role in every oil and gas industry, the understanding of the reservoir rock properties such as porosity and permeability aids engineers enhance reservoir characterization. Reservoir characterization can be defined as the process to describe quantitatively the reservoir characters using the existing data (Aldha, 2009). Heterogeneous reservoirs generally present tough challenges to engineers and geologist in accurately describing the hydraulic flow unit, rock typing, performance and recovery predictions, because of its tendency of being tight and heterogeneous.
For several years petroleum engineers and geoscientists have studied and initiated techniques to improve the reservoir description as it has been a challenge, reservoir characterization methods are completely appreciated because they deliver a much improved and precise characterization of the storage and movement factors of an oil and gas in a reservoir and therefore presents a foundation for developing a simulation model.
In recent studies, porosity-permeability relationship has been used to better the characterization of a reservoir with complex geological continuum. In addition to porosity and permeability, more rock property can be combined to improve the perception to charactering the flow units through porous media such as pore throat scale. (Mike Spearing, 2001) Pore throat plays a significant role in controlling both initial and residual distribution of hydrocarbon.
Hydraulic flow unit (HFU) defines the division of reservoir channels towards different zones with the same flow and bedding characterization, thereby integrating factors like porosity and permeability towards a solo magnitude that defines a formatio n, indicating flow zones and rock typing (Maghsood Abbaszadeh, 1996).
Rock type is a key concept in improving the reservoir description of straddles multiple scales and bridges multiple disciplin es (M. Shabaninejad, 2011). Reservoir rock classification (rock typing) has been a fundamental tool for reservoir characterization, several techniques introduced by several authors has been used to identify rock types in a formation such as FZI, DRT and winland (35), that indicates different flow zones (HFU) for each dissimilar rock type. Parameters involved in these techniques are usually obtained from core data analysis, well logs and well tests, thus in this studies the core data analysis is being used. However, it is difficult predicting properties for uncored well.
The key purpose of this research is to describe the core petrophysical factors necessary for predicting the Hydraulic flow unit, and the rock types transform from 16 wells of an Egyptian reservoir. And also the application of this classification to prepare a reservoir simulation input file accurately to receive an accurate output.

Background Theory

Degree of Heterogeneity

In order to classify the degree of heterogeneity of a reservoir, t the two most widely used descriptors of the heterogeneity of a formation used are Lorenz coefficient, L, and Dykstra-Parsons permeability variation, . Lorenz coefficient introduced by
(Schmalz, 1950) defines the degree of heterogeneity within a sector of a pay zone and varies from 0 to 1, as 0 to be completely

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1367

ISSN 2229-5518

homogenous and 1 to be completely heterogeneous respectively and this can be estimated by plotting a the entire flow capacity
versus the entire volume and applying the equation below:

While Dykstra-Parsons coefficient is one of the worlds most recognized method for measuring the degree of heterogeneity, it is a measure precisely established on permeability variation. (Dykstra, 1950) Describe this method as the statistical degree of data to compute the degree of heterogeneity. This can be estimated using the equation below:
( )
Where V is Dykstra-Parsons coefficient and L is Lorenz coefficient. The value of V can be categorised as follows to classify the
degree of heterogeneity:
- ( ), Slightly heterogeneous reservoir
- ( ), Heterogeneous reservoir
- ( ), Very heterogeneous reservoir
- ( ), Extremely heterogeneous reservoir
- ( ), Perfectly heterogeneous reservoir

Permeability-Porosity Relationship

This approach is the most basic method as it assumes a direct permeability-porosity relationship; this method accepts the entire reservoir as one large hydraulic flow unit with homogeneous properties and singularly unique characteristics (Nelson P. , 1994). Due to this reason the results acquired from this method gives an insufficient description of the reservoir rock properties. Although this method shows the reliant of porosity on permeability of the entire formation and how dependent they are on each other.

Hydraulic Flow Unit

This method describes the quality of an entire reservoir rock in which the geological properties (texture, mineralogy, sedimentary structure, bedding) and petrophysical properties (porosity, permeability, capillary pressure) that affect fluid flow are surely predictable and certainly dissimilar from properties of different rocks. Each flow unit/zone in the reservoir represents a continues lateral, vertical and similar flow and bedding characteristic (Maghsood Abbaszadeh, 1996). (Amaefule O.jude, 1993)
In this approach rock types are classified based on the equation below:

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1368

ISSN 2229-5518

√
Where is effective porosity (fraction), K is permeability (md) and RQI is rock quality index ( ). Additionally core derived
porosity must convert to normalize one as shown below:

Where is normalized porosity. Lastly Flow zone indicator can be calculated by the equation below:
On a log-log plot of RQI versus will be plotted, core samples with the same pore and grain size characteristics will lie on a straight line with a unit slope, while core samples with dissimilar FZI will lie on different parallel lines. To assist in si mplifying the use of rock type in a recreation model, continued FZI values are transformed to discrete rock type (DRT) by equation using the equation below, so as to assist calculate the permeability of each geological model using permeability-porosity relationship of each discrete rock type.
( ( ) )

Permeability Group

In this approach, data are been classified based on their permeability classes; this is to evaluate the effect of permeability on permeability versus porosity plot as shown in Figure 8. Example of permeability classes are described as: K<1mD, 1<K<5mD, 5<K<50mD and K>50mD, a well-defined fit line cannot be acquired for each category using this technique, that could be because of the poor connection between porosity and permeability.

Winland Method (R35)

For several years scientist have made experiments using capillary pressure curve by mercury injection to estimate pore throat sizes. In this approach (Kolodzie, 1980), developed an experimental correlation that relates porosity, permeability and pore throat radius from mercury intrusion tests. The experimental connection of the maximum numerical relationship was attained at the 35% of the cumulative mercury saturation curve, which is donated as (R35). R35 has been considered to estimate the point where the model pore aperture happens, and it is referred to as the point where the pore system is connected creating an on-going route through the core sample. The winland equation is:
( ) ( ) ( )
Where K is the permeability, is the porosity and R35 is the calculated pore throat radius at 35% mercury saturation.
With this in mind (Katz, 1986) confirmed that this case is only correct if the pore throat size is equivalent to the point of inflexion of the pore throat size verse mercury saturation. R35 of a particular rock type will always have the same values. Below are the five-petrophysical flow
units with distinctive reservoir performance differentiated by the extension of the R35 standard:

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1369

ISSN 2229-5518

- Mega-porous units, expressed by R35 greater than 10 microns.
- Macro-porous units, expressed by R35 between 2.5 and 10 microns
- Meso-porous units, expressed by R35 between 0.5 and 2.5 microns
- Micro-porous units, expressed by R35 between 0.2 and 0.5 microns
- Nano-porous units, expressed by R35 smaller than 0.2 microns

Data Used

The following data is extracted from core samples of 16 different wells of an Egyptian field, consisting of porosity and permeability with depths of each well. Before conducting the experiments, the quality of all the samples were checked, a few samples were broken or unavailable due to miss handling of core samples; therefore, they were not included in our calculations to ensure accurate readings only.

Results and Discussion

Degree of Heterogeneity – Fig 1 shows a plot of normalized cumulative permeability capacity against normalised porosity capacity, which displays a curve that shows the degree of heterogeneity as calculated using Lorenz coefficient the area between the curve and the straight line = 0.78, which categorises this field as extremely heterogeneous reservoir. This indicate the presence of different lithology and rock types, secondly applying dykstra-parsons permeability variation equation to certify the

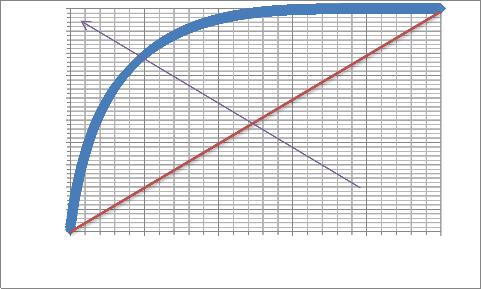
degree of heterogeneity also estimated a value of 0.80 which also indicates the field to be Extremely heterogeneous reservoir.

1

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0

Increasing

heterogeneity

0 0.2 0.4 0.6 0.8 1

Normalised Porosity Capacity

Figure 1: Lorenz Coefficient

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1370

ISSN 2229-5518

While, when dykstra-parsons permeability equation is been applied

Permeability-Porosity relationship – A power relationship between log permeability and porosity is obtained, Fig 2 shows a classic permeability and porosity relationship for the entire reservoir. As show in the figure, there is a poor relationship between

permeability and porosity ( ); this method is not ideal for rock type determination in a reservoir. The obtained

value neglected the scattering of the data and predicted a smoothed permeability prediction.

100000.00

10000.00

1000.00

100.00

10.00

1.00

y = 0.3252e0.3644x

R² = 0.4997

0.10

0.01

0.00 10.00 20.00 30.00 40.00

Porosity (%)

Figure 2: Permeability Versus Porosity

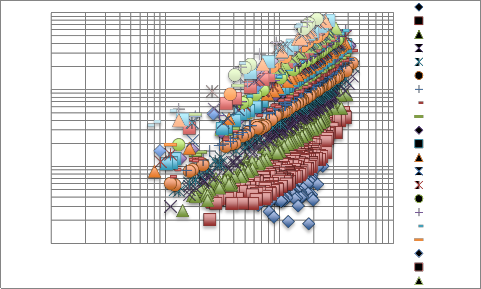
Flow Zone Indicator (FZI) – Fig. 3, Show the plot of RQI and normalised porosity based on FZI value. As illuminated in this figure, all data laying in the same colour presents accurate straight-line correlations with unit slope of equal FZI value as shown in Table 1. According to the data in this figure, the entire field displays 35 FZI that confirms 35 HFU; this could be because of the heterogeneity of the reservoir. It is also due to know that rock type with the highest FZI value has the better quality of fluids

flow in the pore spaces of the reservoir rock. Fig. 4 illustrates the plot of permeability versus porosity classified based on FZI.

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1371

ISSN 2229-5518

10

1

0.1

0.01

0.001 0.01 0.1 1

Normalised Porosity

FZI = 0

FZI = 1

FZI = 2

FZI = 3

FZI = 4

FZI = 5

FZI = 6

FZI = 7

FZI = 8

FZI = 9

FZI = 10

FZI = 11

FZI = 12

FZI = 13

FZI = 14

FZI = 15

FZI = 16

FZI = 17

FZI = 18

FZI = 19

FZI = 20

Figure 3: Reservoir Quality Index Versus Normalised Porosity

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

0.01

0.001 0.01Porosity (fracti0o.n1)

FZI = 0

FZI = 1

FZI = 2

FZI = 3

FZI = 4

FZI = 5

FZI = 6

FZI = 7

FZI = 8

FZI = 9

FZI = 10

FZI = 11

FZI = 12

FZI = 13

FZI = 14

FZI = 15

FZI = 16

FZI = 17

FZI = 18

1 FZI = 19

FZI = 20

Figure 4: Permeability Versus Porosity Based on Flow Zone Indicator

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1372

ISSN 2229-5518

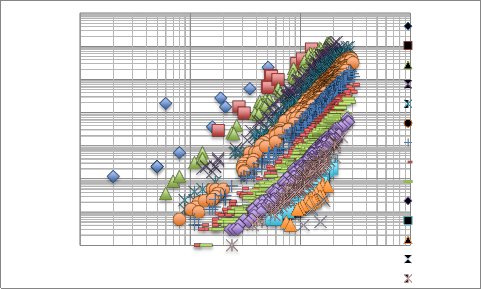
Although Fig 3 and Fig 4 are accurate, the huge amount of flow zone is a problem in the application to reservoir simulator, that which will indicate the presents of lots for formation and will consume time. Therefore, Fig 3 and Fig 4 needs to be modified to reduce the number of flow unit with a degree of accuracy, so as to easily acquire a more précised and accurate reservoir characterisation. Fig 5 shows the plot of a modified RQI versus normalised porosity with a display of 12 FZI that confirms 12
HFU with a degree of accuracy as shown in Table 2 for each FZI. Fig. 6 also illustrates the modified plot of permeability versus

porosity classified based on FZI.

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

0.01

FZI = 92

FZI = 55

FZI = 37

FZI = 26

FZI = 18

FZI = 11

FZI = 7

FZI = 4

FZI = 3

FZI = 2

FZI = 1

0.001 0.01 0.1 1

Porosity (fraction)

Figure 5: Modified Plot of Reservoir Quality Index Versus Normalised Porosity

10

1

0.1

0.01

FZI = 92

FZI = 55

FZI = 37

FZI = 26

FZI = 18

FZI = 11

FZI = 7

FZI = 4

FZI = 3

FZI = 2

0.001 0.01 0.1 1 FZI = 1

Normalised Porosity

Figure 6: Modified Plot of Permeability Versus Porosity Based on Flow Zone Indicator

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1373

ISSN 2229-5518

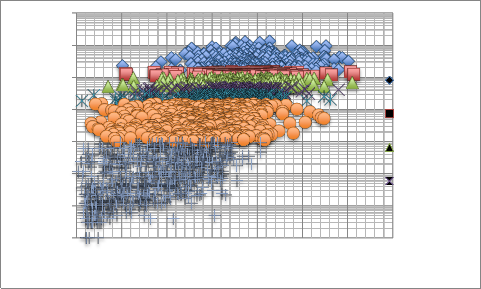
Discrete Rock Types – Fig 7 shows a plot of permeability versus porosity based on DRT values for the entire field, as illustrated in this Figure DRT simplifies the flow units in order to make an easier application of rock type in the simulation models for a more accurate and less time consuming results. Also, the DRT values have a correlation in each well with similar DRT values that

indicates the connection of all 16 wells, as shown in Table 3 showing wells with similar DRT values.

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

0.01

DRT = 20

DRT = 19

DRT = 18

DRT = 17

DRT = 16

DRT = 15

DRT = 14

DRT = 13

DRT = 12

DRT = 11

DRT = 9

DRT = 8

0.001 0.01 0.1 1DRT = 7

Porosity (fraction)

DRT = 10

Figure 7: Permeability Versus Porosity Based on Discrete Rock Type

Permeability Group – Fig 8 shows a plot of permeability versus porosity in order of permeability intervals as illustrated this figure for the entire field. According to this figure, zones that happen to have the highest permeability values has a better quality of fluids flow in the pore spaces of the reservoir.

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1374

ISSN 2229-5518

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

K >1500

1000 < K

<1500

1000 < K <

1000

300 < K <500

0.01

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

Porosity (fraction)

Figure 8: Permeability Versus Porosity Based on Permeability Grouping

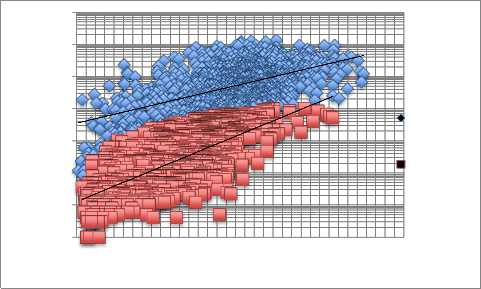
Winland Method - routine core data gathered for each well was calculated using winland equation, winland R35 plot of the entire field shown in Figure 9, as illustrated the core data covers two parts of the plot surface that means the existence of separate rock types. Following the winland categories, the entire field where classified into two (Marco-porous and Meso-porous) pore scale with 4 different value of R35 (1, 2, 3, 4) as shown in this figure, as observed in both FZI and DRT, rock types with the highest value of pore throat radii have the better quality index to flow fluids through porous media. In addition to winland, Figure 10

illustrates the plot of permeability and porosity based on winland R35 category method.

100000.00

10000.00

R² = 0.81102

1000.00

100.00

R² = 0.44423

R35 = 3 - Macroport

10.00

1.00

0.10

R² = 0.62358

R² = 0.59968

R35 = 4 -

Macroport R35 = 2 - Mesoport R35 = 1 - Mesoport

0.01

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

Porosity

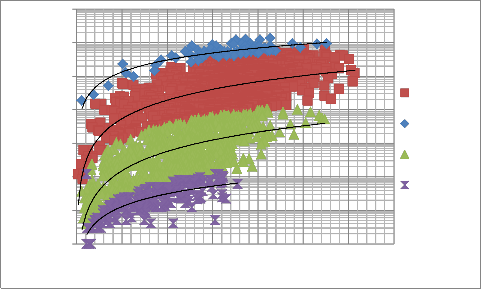
Figure 9: Rock Type Classification based on Winland R35

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1375

ISSN 2229-5518

100000.00

10000.00

1000.00

100.00

10.00

1.00

R² = 0.33181

R² = 0.49607

Macroport

Mesoport

0.10

0.01

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35

Porosity

Figure 10: Permeability Versus Porosity as classified by Winland R35

Additionally, (Nelson P. H., 2005) examined the relationship between permeability, porosity and pore-throat to three different plots, as applied to our data as shown in Fig 11, Fig 12 and Fig 13 (permeability versus R35, permeability versus porosity*R35, permeability versus porosity*(R35)^2) respectively classified based on winland method and also Fig 14, Fig 15 and Fig 16 (permeability versus R35, permeability versus porosity*R35, permeability versus porosity*(R35)^2) respectively. In respect to the result, all three correlations displays a good relationship but Fig 13 and Fig 16 show much higher consistency with
coefficient of determination ( ).

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

R² = 3.8E-06

R² = 0.72549

R² = 0.67058

R² = 0.20144

R35 = 4 - Macroport

R35 = 3 - Macroport

R35 = 2 - Mesoport

R35 = 1 - Mesoport

0.01

0.1 1 10

R35

Figure 11: Permeability Versus R35 based on Winland R35 method

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1376

ISSN 2229-5518

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

0.01

R² = 0.84189

R² = 0.61244

R² = 0.77264

R² = 0.85543

R35 = 4 - Macroport

R35 = 3 - Macroport

R35 = 2 - Mesoport

R35 = 1 - Mesoport

0.001 0P.0o1rosity*R35

0.1 1

Figure 12: Permeability Versus Porosity*R35 based on Winland R35 method

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

0.01

R² = 0.87149

R² = 0.75205 R² = 0.8893

R² = 0.95833

R35 = 4 - Macroport

R35 = 3 - Macroport

R35 = 2 - Mesoport

R35 = 1 - Mesoport

0.00

0.01 0.1 Porosity*(R3 1 ^2 10

Figure 13: Permeability Versus Porosity*(R35)^2 Based on Winland R35 Method

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1377

ISSN 2229-5518

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

0.01

0.00

0.00

y = 0.007x10.065

R² = 0.9065

0.1 1 10

R35

Figure 14: Permeability Versus R35

100000.00

10000.00

1000.00

100.00

10.00

1.00

0.10

0.01

0.00

0.00

y = 3140.3x3.3308

R² = 0.7604

0.001 0.01 0.1 1

Porosity*R35

Figure 15: Permeability Versus Porosity*R35

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1378

ISSN 2229-5518

100000.00

10000.00

1000.00

y = 134.72x2.8252

R² = 0.8994

100.00

10.00

1.00

0.10

0.01

0.00

0.01 0.1 1 10

Porosity*(R35)^2

Figure 16: Permeability Versus Porosity*(R35)^2

Application

Based on the results acquired from the research, the permeability equations obtained through FZI and DRT can be used to calculate the permeability with an acceptable accuracy and reliability to assign properties for each zone. A full idea of the entire reservoir is understood with the number of flow zone or rock type known. This helps us know the boundaries of each reservoir (Zone) after divided into girds and cells to be used in reservoir simulator, in this case we understand how to estimate the initial and boundary condition for each reservoir (zone). Finally before going to reservoir simulation, in order to calculate the reserve, initial gas in place, initial oil in place and field development planning it is very important to prepare a relative permeabi lity curve, build up pressure, compressibility and PVT for each zone, so as to create an accurate input data or file of reservoir simulation to achieve an accurate reservoir characterisation output.

Conclusion

Reservoir characterisation should be the first step before the start reservoir simulation in order to establish the input file for each reservoir rock type that can be used in any reservoir simulation. Most oil and gas industries face the challenge when dealing with heterogonous reservoirs or when working with reservoir simulation in general because they don’t study the reservoir characterisation before any start of reservoir simulation which has lead most enhanced oil recovery and secondary recovery projects to fails. The most common approaches for characterising reservoir and analysing the reservoir rock type were investigated in this research for an extremely heterogeneous field and including Flow Zone Indicator, Discrete Rock Type, permeability-porosity relationship, permeability grouping and winland R35 method. In accordance to the result permeability- porosity relationship approaches was incapable of identifying the rock type due to high heterogeneity in this reservoir, winland
R35 method classified the reservoir into Macro-porous and Meso-porous pore scale media and both FZI and DRT classified the

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1379

ISSN 2229-5518

reservoir into 13 and 14 flow unit respectively that which indicates 14 rock types. Nevertheless, the accuracy of all this methods relies on the kind of reservoir and may differ with different rock properties Furthermore, reservoir characterisation is very important in order to have a good image about our reservoir and to prepare an accurate input files that can be used in any reservoir simulation.

Acknowledgments

The authors would like to extend their wholehearted gratitude to the British University in Egypt, Petroleum Engineering Dept. for supporting this research work.

Bibliography

1. Aldha, T. (2009). Carbonate Reservoir Charaterization Using Simultaneous Inversion, Batumerah Area, South Papua, Indonesia. UNIVERSITY OF INDONESIA, FACULTY OF MATHEMATICS AND NATURAL SCIENCES. Universitas Indonesia.

2. Amaefule O.jude, M. A. (1993, october 6). Enhanced Reservoir Description: Using Core And Log Data To Identify Hydraulic (flow ) Units and

Predict Permeability in Uncored intervals/wells.

3. Carman, P. (1939). Permeability of saturated sands soild and clays. Journal of Africultural science .

4. Choper, A. (1988). Reservoir Description Via Pulse. SPE internation .

5. Costa, A. (2006). Permeability-Porosity relationship: A reexamination of the Kozeny-Carman Equation Based on a fractal pore-space geometry assumption. Geophysical Research Letters , 5.

6. Dykstra, H. a. (1950). The prediction of oil recovery by water flood. Secondary Recovery of Oil in the United States .

7. Donalson, D. T. (2004). Petrophysics. Theory and practice of measuring resrvoir rock and fluid transport properties (Vol. 2). Gulf Professional

Publishing.

8. Katz, A. a. (1986). Quantitative prediction of permeability in porous rock. Physical Review .

9. Kolodzie, S. (1980). Analysis of Pore Throat Size and Use of the Waxman-Smits Equation to Determine OOIP in Spindle Field. SPE INternational .

10. Nelson, P. H. (2005). Permeability, Porosity and Pore-throat size- A Three-Dimensional Perpective. Society of Petrophysicists and Well-Log

Analysts , 46 (6), 4.

11. Nelson, P. (1994). Permeability-Porosity Relationships in sedimentary rocks. The log analyst , 38-62.

12. M. Shabaninejad, M. B. (2011, August 3). Rock Typing and Generalization Og Permeability-Porosity Relationship for an Inranian Carbonate

Gas Reservoir. SPE International , 7.

13. Maghsood Abbaszadeh, H. F. (1996, December ). Permeability prediction by Hydraulic flow units -Theory and applications. SPE international .

14. Mike Spearing, T. a. (2001). Review of the Winland R35 Method for net Pay Definiation and its appilicationin low permeability sands.

Proceedings of the 2001 International Symposium of the Society of Core Analysts, paper SCA 2001 -63. .

15. Schmalz, J. P. (1950, July). The variation in water flood permance with variation inpe rmeability profilr. Producers Monthly .

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1380

ISSN 2229-5518

Table 1: Characterisation of 35 Rock Types

Based on FZI

Table 2: Characterisation of 12 Rock Types

Based on FZI

IJSER © 2015

http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 1381

ISSN 2229-5518

Table 3: Characterization of 14 Rock Types

Based on DRT

IJSER © 2015

http://www.ijser.org