International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 166
ISSN 2229-5518
High-Resolution Automated Fingerprint
Recognition System (AFRS) based on Gabor wavelet and SVM
Hamed Mohammadi Jirandeh, Hamed Sadeghi, Mohammad Amir Javadi Rad
Abstract— motivated by the desire to construct efficient biometric systems, we propose a fingerprint identification system based on Gabor wavelet and Support vector Machine (SVM).We demonstrate that the Gabor wavelet based on features can capture textural information at different scales and orientations and it can achieve high recognition rates utilizing well-tuned SVM. Also, we introduce optimal filter in terms of accuracy and time complexity by changing the parameters of Gabor wavelet. Results obtained from the polyu HRF dataset show that the accuracy of the proposed system is comparable to that obtained using other well-known systems.
Index Terms— Gabor wavelet, SVM, Fingerprint Recognition, Biometric.
—————————— ——————————
1 INTRODUCTION
s one of the most popular biometric attributes, the finger- print is widely used in the verification of identity. Most fingerprint recognition techniques making use of minutiae as fingerprint feature. Using these methods has some problems, because the image must be pre-processed before extracting features. The main steps for minutiae extraction are smooth- ing, local ridge orientation estimation, ridge extraction, thin- ning, and minutiae detection [1]. So the accuracy of the system is related to the accuracy of all steps. Another method of fin- gerprint recognition is using texture features as a feature vec-
tor. A method for extracting textural features is using the Ga-
posed system is assessed on polyu HRF data set. The results of experiments confirm the effectiveness of the proposed system.
This paper is organized as follow: Section 2 describes in de- tail Gabor wavelet. Section 3 describes support vector machine algorithm. In section 4, we describe proposed system. In sec- tion 5, we describe experimental results.your paper.
2 GABOR WAVELET
Gabor wavelet function is as follows:
1 −�𝑥0 0 2 2 2
bor wave-let. Gabor filter-based features have been successful and widely applied to texture segmentation [2], face recogni-
𝛹(𝑥0 , 𝑦0 , 𝜔0 , 𝜃) = 2𝜋𝜎2 𝑒
2+𝑦2�⁄2𝜎
�𝑒
𝑗𝜔0𝑥0
− 𝑒
𝜔0 𝜎 ⁄2
� (1)
tion [3], handwriting recognition [4] and fingerprint enhance- ment [5]. This is because the characteristics of the Gabor filter, especially the frequency and orientation representations, are similar to those of the human visual system [6]. The receptive field space structure of the mammalian visual simple cortical cell can be described with Gabor mathematic function [7]. It has some great properties such as space position selection,
Where 𝑥0 = 𝑥 cos 𝜃 + 𝑦 sin 𝜃 , 𝑦0 = −𝑥 sin 𝜃 + 𝑦 cos 𝜃, x and y are the position of pixel. The center frequency is 𝜔0. The orien- tation of the Gabor wavelet determines by 𝜃. The norm vari- ance of Gauss function is 𝜎. So in (1), 𝜔0 controls the Scale of Gabor filters and 𝜃 controls the orientation of Gabor filters. In
this paper, five center frequencies are used as follows:




1 2 3 4 5
direction selection, frequency selection and orthogonally. It
extracts the Gabor wavelet coefficients of different direction
and scale as features from data gray distribution [8].
Recently, high resolution (≥ 1000ppi) fingerprint images
have been increasingly used for fingerprint recognition com-
pared with traditional low-resolution (~500ppi) fingerprint
images, they offer better features on fingerprint and thus it can
help to further improve the fingerprint recognition accuracy [9]. In this paper, features directly are extracted from finger- print images by Gabor wavelet without any pre-processing. Then, a SVM classifier is used to learn the data set. The pro-
————————————————
• Hamed Mohammadi Jirandeh, Department of Electrical engineering, Alborz
Institute of Higher Education, Qazvin, Iran. E-mail: hamedmit@yahoo.com
• Hamed Sadeghi, Department of Electrical engineering, Alborz Institute of
Higher Education, Qazvin, Iran. E-mail: h.sadeghi@znu.ac.ir
• Mohammad Amir Javadi Rad, Department of Electrical engineering, Alborz
Institute of Higher Education, Qazvin, Iran. E-mail: amir_rad501@yahoo.com

𝜔0 = √2 𝜋⁄2 , 𝜔0 = √2 𝜋⁄3 , 𝜔0 = √2 𝜋⁄4 , 𝜔0 = √2 𝜋⁄5 , 𝜔0
= √2 𝜋⁄6
The orientation parameter 𝜃is selected as follows:
𝜃1 = 0, 𝜃 2 = 𝜋⁄4, 𝜃 3 = 𝜋⁄2, 𝜃 4 = 3𝜋⁄4 .
Also, we set 𝑘𝑚𝑎𝑥 = 𝜋⁄2
3 SUPPORT VECTOR MACHINE
SVM is developed based on statistical learning theory [10]. SVM has a very good performance for high-dimensional and is non-linear pattern classification problem by minimizing the Vapnik-Chervonenkis dimensions and achieving a minimal structural risk [11]. Suppose that the training set be as follows:
𝐷 = �(𝑥𝑖 , 𝑦𝑖 )|𝑥𝑖 ∈ 𝑅𝑝 , 𝑦𝑖 ∈ {−1,1}� ; 𝑖 = 1, … , 𝑛
Where 𝑦𝑖 = 1, 𝑦𝑖 = −1which Defines the 𝑥𝑖 class. 𝑥𝑖 is a 𝑝 di-
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 167
ISSN 2229-5518
mensional vector. The goal is to find hyper plane with the
maximum margin that can separate the points having 𝑦𝑖 =
1from those having 𝑦𝑖 = −1.
Solving optimal hyper plane can be modeled as a quadratic
programming problem. For given training samples, optimal
weight 𝑤 and offsets 𝑏 for the minimizing cost function weight
is found. When the training samples are separated and are
nonlinear, auxiliary variable 𝜉 𝑖 ; 𝑖 = 1, … , 𝑙 is used. So the
classification problem can be considered as a hyper plane op-
timization problem as follows:
deter-mined and by using training set, Support Vector Ma- chine trained and the optimal decision function is obtained. RBF is intended as kernel function, kernel argument and regu- larization content are selected 27 and 9 respectively.
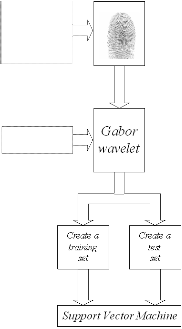
Acquisition Device
Fingerprint image 1
Fingerprint image 2
.
.
.
Fingerprint image n
min 𝜑(𝑥) = 1 ‖𝑤‖2 + 𝐶 ∑𝑙 𝜉
(2)

2 𝑖=1 𝑖
𝑠. 𝑡 𝑦𝑖 (𝑤. 𝑥𝑖 + 𝑏) ≥ 1 − 𝜉 𝑖
𝜉 𝑖 ≥ 0; 𝑖 = 1, … , 𝑙
In these equations, 𝐶 is the penalty parameter, which, can
help to reduce the number of training errors. After solving the
optimization problem, the corresponding optimal decision is as follows:
parameter
Scale=5
Orientation=4
𝑙 ∗ ∗
Feature vector
𝑓(𝑥) = 𝑠𝑔𝑛�∑𝑖=1 𝑦𝑖 𝛼𝑖 𝐾(𝑥, 𝑥𝑖 ) + 𝑏 �. (3)
4 PROPOSED SYSTEM
In this paper, fingerprint identification method based on Gabor wavelet and support vector machine have been pro- posed. Initially, Gabor wavelet features of finger-print sam- ples are extracted and a training set is created. Then the SVM is trained by this training set and optimal classification deci- sion function is computed.
4.1 Gabor wavelet feature extraction
Initially Gabor wavelet filter mask is created according to
(1). Assuming that 𝐼(𝑥, 𝑦) is finger-print image and
𝐺𝑚,𝑛 (𝑥, 𝑦) is Gabor wavelet filter mask. Next, image should be
convolution with mask, namely:
𝐼𝑚,𝑛 (𝑥, 𝑦) = 𝐼(𝑥, 𝑦) ∗ 𝐺𝑚,𝑛 (𝑥, 𝑦)
𝐼𝑚,𝑛 (𝑥, 𝑦) is contain of extracted features. In this paper, im-
age size and mask size are considered equal. If the mask and
image size be 𝑀 × 𝑁, then size of 𝐼𝑚,𝑛 (𝑥, 𝑦)will be 𝑀 × 𝑁. To create a feature vector, 𝐼𝑚,𝑛 (𝑥, 𝑦) is divided into 4 blocks and
the mean and standard deviation for each block are computed.
Finally, a feature vector matrix 1 × 160 is obtained.
𝑉 = [𝜇11, 𝜎11 ; 𝜇12, 𝜎12 ; 𝜇13 , 𝜎13 ; 𝜇14 , 𝜎14 ; … ; 𝜇𝑝𝑞 , 𝜎𝑝𝑞 ]
Where number of filters is p and q is number of blocks. In
this paper, 20 Gabor wavelet filter is applied to the fingerprint
image, which the scale S = 5, and orientation O = 4 are select-
ed.
4.2 SVM fingerprint recognition
As it can be seen in Fig. 1, from extracted features by Gabor wavelet training set and test set are created. According to var- ious classes of training samples, the samples are labeled from
1 to N. where N is the number of people. In next step the ker- nel function and parameters of Support Vector Machine are
Fig. 1. block diagram proposed system
5 EXPERIMENTAL RESULTS
In this paper we have used the polyu HRF database [12]. Papers [13], [14], [15] have used from this database for their experiments. Examples of this database are shown in Fig. 2.

Fig. 2. Examples of database
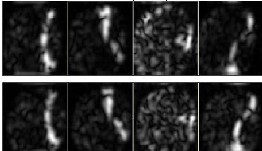
Fig. 3 shows magnitude Gabor features of two fingerprints belonging to one person. Fig. 4 shows magnitude Gabor fea- tures of two fingerprints belonging to different two-person. Fig. 3 and Fig. 4 shows that the magnitude Gabor features of two fingerprints belonging to one person are very similar and the magnitude Gabor features of two fingerprints belonging to two different persons are different. So we can use magnitude
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 168
ISSN 2229-5518
Gabor features as features.
500
400
300
200
100
0
parameters
Fig. 3. magnitude Gabor features of two fingerprints belonging to one person
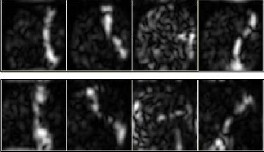
Fig. 4. magnitude Gabor features of two fingerprints belonging to different two-person
We have chosen 500 fingerprint images from 50 people (10 photos per person) for the experiment. For training set, 6 im- ages per person and for test set others of four images have used. Experimental results show accuracy of 95.5%. About choice of scale for Gabor wavelets, experiments are performed with further scales and direction. As illustrated in Fig. 5 and Fig. 6, the results in terms of both time complexity and error rate are compared. As can be seen in Fig. 2, in best filter scale=
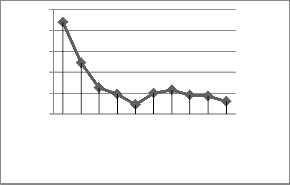
5 and orientation = 4.
0.5
0.4
0.3
0.2
0.1
0 Parameters
Fig. 5. Error rate of various parameters
In this paper, experiments were done using a computer with MATLAB R2009a software. Computer configuration is Intel core i3 processor and 4 GB RAM.
Fig. 6. time complexity of various parameters
6 CONCLUSION
In this paper fingerprint feature extraction by Gabor wave- let filter and their classification by Support Vector Machines are presented. Gabor wavelet filter is controlled by two pa-
rameters 𝜔0and 𝜃 after which Comparison of various parame-
ters we introduced appropriate Gabor wavelet filter. Then, the
extracted features, training the Support Vector Machine and
the rest is considered as test set. Experiments show that the
method is very accurate and its value is equal to 95.5%. Ac-
cording to the results of Chapter 5, scale = 5 and orientation =
4 is considered for filter.
ACKNOWLEDGMENT
This research supported by Alborz Institute of Higher Edu- cation.
REFERENCES
[1] A. Jain, Lin Hong, R. Bolle, “On-line fingerprint verification,” IEEE Trans.
Pattern Analysis and Machine Intelligence, vol. 19, pp. 302-314, 1997.
[2] T.P. Weldon, W.E. Higgins, D.F. Dunn, “Efficient Gabor filter design for texture segmentation,” Science Direct. Pattern Recognition, vol. 29, pp. 2005-2015, December 1996.
[3] J. Lampinen, E. Oja, “Distortion tolerant pattern recognition based on self-organizing feature extraction,” IEEE Trans. Neural Networks, vol.
6, pp. 539-547, 1995.
[4] Y. Hamamoto, S. Uchimura, M. Watanabe, T. Yasuda, Y. Mitani, S.
Tomita, “A Gabor filter-based method for recognizing handwritten numerals,” Pattern Recognition, Vol. 31, pp. 395-400, April 1998.
[5] L. Hong, Y., Wan, A., Jam, “Fingerprint image enhancement: algo- rithm and performance evaluation,” IEEE Trans, Vol. 20, pp. 777-789,
1998.
[6] J.G. Daugman, “Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cor- tical filters,” Optical Society of America, Vol. 2, No. 7, pp. 1160-1169, Ju- ly 1985.
[7] J.G. Daugman, "Complete discrete 2-D Gabor transforms by neural networks for image analysis and compression," IEEE Trans. On Acoustics Speech and Signal Processing, Vol. 16, pp. 1169-1179, July,
1988.
[8] Zhang Guo-yun, Guo Long-yuan, Wu Jian-hui, Li Hong-min, Guo Guan-qi, “Face detection using Gabor wavelet and SVM,” Interna- tional Conference. Computer Application and System Modeling (ICCASM),
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 5, May-2014 169
ISSN 2229-5518
vol. 2, pp. V2-588 - V2-590, 2010.
[9] A.K. Jain, Y. Chen, and M. Demirkus, "Pores and Ridges: High- Resolution Fingerprint Matching Using Level 3 Features," IEEE Trans. PAMI, vol. 29(1), pp. 15-27, 2007.
[10] Qing SONG, Hui YUAN, Xisheng LIU, Chen QIU, “Support Vector Machine forthe Liquid Drop Fingerprint Recognition,” IEEE Confer- ence Publications, pp. 280 - 282, 2012.
[11] V. Cherkassky, “The nature of statistical learning theory,” IEEE
Trans. Neural Networks, vol. 6, pp. 1564, Nov 1997.
[12] The Hong Kong Polytechnic University (PolyU) High Resolution- Fingerprint(HRF)Database. http://www4.comp.polyu.edu.hk/~biometrics/HRF/HRF.htm.
[13] D. Zhang, Feng Liu, Qijun Zhao, Guangming Lu, Nan Luo, “Select- ing a Reference High Resolution for Fingerprint Recognition Using Minutiae and Pores,” IEEE Trans. Instrumentation and Measurement, VOL. 60, PP. 863-871, 2011.
[14] Qijun Zhao, D. Zhang, Lei Zhang, Nan Luo, “High resolution partial fingerprint alignment using pore–valley descriptors,” Science Direct. Pattern Recognition, vol. 43, pp. 1050-1061, March 2010.
[15] Qijun Zhao, D. Zhang, Lei Zhang, Nan Luo, “Adaptive fingerprint
pore modeling and extraction,” Science Direct. Pattern Recognition, vol.
43, pp. 2833–2844, August 2010.
IJSER © 2014 http://www.ijser.org





