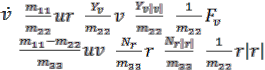International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 1

ISSN 2229-5518

Formation Control of Multiple AUV’s In

Horizontal Plane Using Leader-Follower Approach

Deepali Chandrakar, Dewashri Pansari, Bharti Dewani

Abstract- Formation control using a leader-follower approach is a advancement in AUV technology for control and formation of multiple Autonomous underwater vehicles. This approach leads the other approaches of formation control like behaviour-based method, virtual structural method, artificial potentials as the theoretical formalization and mathematical analysis of these approaches are difficult and consequently it is not easy to guarantee the convergence of the formation to a desired configuration. On the other hand in the leader-follower approach, a robot of the formation, designated as the leader, moves along a predefined trajectory while the other robots, the followers, are to maintain a desired distance and orientation with respec t to the leader. Numerical simulations are carried out to illustrate the effectiveness of the proposed formation scheme.

Index Terms— Multiple AUV system, Formation control, Kinematics, Dynamics, Leader, Follower, Degree of freedom.

1 INTRODUCTION

——————————  ——————————
In many applications, a given task is too complex to be
accomplished by a single robot; thus a multi-robot system
An autonomous underwater vehicle (AUV) is a robot
which travels underwater without requiring input from an operator. With the increase in technology and applications of AUV in different areas lots of attentions have been paid to the research on the cooperative control and formation control of multiple autonomous agents, especially on the cooperative control of groups of robots. History says that In 1987, Reynolds introduced a distributed behavioral model for flocks, herds and schools [6] where the three heuristic rules that of flock centering, collision avoidance and velocity matching were also introduced. In [6], each of dynamic agents was considered as a certain particle system whose dynamics can be expressed as a simple second-order linear equation. Furthermore, this kind of dynamic agents (particles) model was used in many of the following researches [4], [10].Soon It was realized that multiple autonomous agents can be used to carry out more complicated jobs for single agent hard to finish. The recent advances in sensing, communication and computation enable the conduct of cooperative missions.

————————————————

 Deepali Chandrakar is currently Pursuing Masters Degree program in Electrical Devices and Power System engineering in DIMAT, Raipur, India,

ph-09098779021.

E-mail:deepali_chandrakar028@yahoo.co.in.

 Dewashri pansari is currently Perusing Masters Deegre in Electrical Devices and Power System engineering in DIMAT, Raipur, India, ph-09770145207.
E-mail: pansaridewashri@gmail.com.
 Bharti dewani is currently working as a Assistant professor in deptment of Electrical and Electronics Engineering in DIMAT Raipur, India, ph- 09981131051

E-mail- bharti.dewani@gmail.com

working cooperatively is required to complete the job. Multi- robot systems are more robust as compared to the single-robot systems because a team of robots provides certain amount of redundancy, which is useful when some of the robots malfunction also less time is needed to complete the job e.g. the use of AUVs for offshore operations includes ocean sampling, mapping, minesweeping, ocean floor survey, and oceanographic data collection. Instead of a single specialized expensive AUV, it is beneficial to use comparatively simple and inexpensive AUVs to cooperatively increase the service area.
In this paper the leader-follower formation control can be
achieved as the leader AUV has to track the desired trajectory and the follower AUV tries to maintain a desired distance and angle relative to the leader. When all vehicles are in expected positions, the desired formation is established.

2 MODELLING OF AUV’S

To study the motion of marine vehicle 6 degrees of freedom are required since to describe independently the complete position and orientation of the vehicle we require 6 independent coordinates.[8] To describe position and translation motion first three sets of coordinates and their time derivatives are required.
While for orientation and rotational motion last three sets of coordinates and their time derivatives are required. Table I shows this DOF.

TABLE I

NOTATION USED FOR AUV MODELLING

International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 2

ISSN 2229-5518

Xb is the longitudinal axis,Yb is the transverse axis, and Zb is
the normal axis. The kinematic equations of motion for an
AUV on the horizontal X-Y plane can be written as
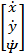= (1) (Linear) surge (forward) and sway (side) velocities,
respectively, defined in the body fixed frame. The orientation

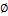
of the vehicle is described by angle Ψ measured from the

inertial X-axis and r is the yaw (angular) velocity. Assuming that (i) the CM coincides with the centre of buoyancy (CB) (ii) the mass distribution is homogeneous, (iii) the hydrodynamic drag terms of order higher than two are negligible, and (iv)

heave, pitch and roll motions can be neglected, the dynamics

is expressed by the following differential equations:
To obtain a mathematical model of the AUV, its study can
be divided into two sub-categories: Kinematics and Dynamics.
Kinematics deals with bodies at rest or moving with constant velocity whereas dynamics deals with bodies having accelerated motion

2.1 AUV kinematics and dynamics

To study the planar motion, we define an inertial frame {I} and a body fixed frame {B}. The origin of {B} frame coincides with the AUV centre of mass (CM) while its axes are along the principal axes of inertia of the vehicle.

Fig. 1 AUV diagram showing inertial and body fixed frames

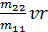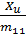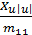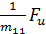= - - + (2)

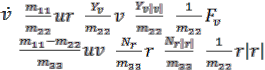
= - - + (3)
= - - + (4)
The variable Fu denotes the control force along the surge motion of the vehicle and variable Fv denotes the control force along the sway motion of the vehicle. Third equation is uncontrolled and the AUV is an underactuated dynamic system. The constants m11 and m22 are the combined rigid body and the added mass terms, and m33 is the combined rigid body and added moment of inertia about Zb axis. Xu, Xu|u| , Yv, Yv|v|, Nr and Nr|r| are the linear and quadratic drag terms coefficients.

2.2 Reference path and controller design

We choose a reference circular inertial planar trajectory given as follows
Xr(t) = 8sin(0.01t) m, (5) Yr(t) = 8cos(0.01t) m. (6)
From this reference path, we find the error in position actual position – reference position). This error is then given to proportional derivative controller (PD controller) which generates necessary controlling signals. The output from controller is then feed to system (AUV) which reduces the error in position and thus, AUV tracks the

International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 3

ISSN 2229-5518

desired trajectory. The reference path for follower AUV is
the circle with same frequency but with different radius.

3 SIMULATION NUMERICAL DATA’S

Here some numerical data’s are considered for simulation
 Mass (M)-185 Kg

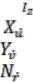
 Rotational mass - 50 kgm2
 Sway linear drag Yv

- 100 kg/s
 Added mass - 30 Kg
 Added mass - 80 Kg
 Added mass - 30 kgm2
 Surge linear drag Xu -70 kg/s
 Surge quadratic drag Xu|u| - 100 kg/m
Sway quadratic drag Yv|v|- 200 kg/m
 Yaw linear drag Nr - 50 kgm2/s
 Yaw quadratic Nr|r| -100 kgm2
Also, m11 = m - 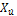= 215 kg, m22 = m - 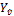= 265 kg, m33 = m - 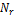= 80 kgm

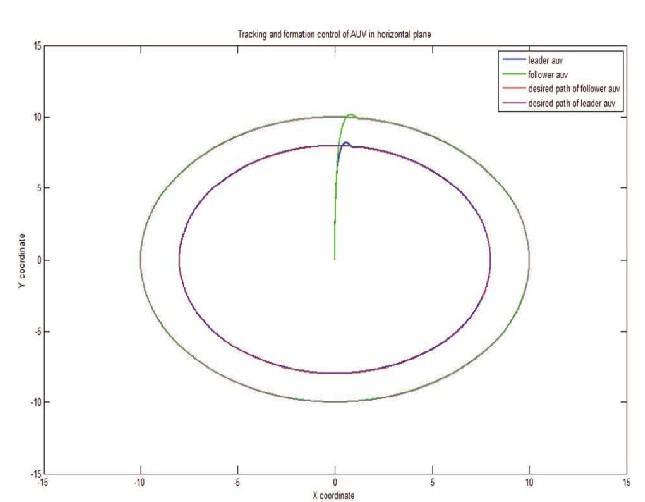
Fig 2. Tracking and formation control of AUVs in horizontal plane

International Journal of Scientific & Engineering Research, Volume 3, Issue 10, October-2012 4

ISSN 2229-5518

The leader AUV is tracking its desired path which is a
circle of radius 8m and also the follower AUV is maintaining a constant distance of 2m from the leader AUV.

4 CONCLUSIONS

In this paper modelling of AUV is done and kinematics and dynamic equations of motion were obtained. Through simulation of this model we obtain a stable formation scheme for multiple AUV system, Therefore, for the simplification purpose, only formation of the vehicles in horizontal plane not in 3D plane and without obstacle avoidance is considered in this paper. However, from the design procedure presented in this paper, it is not difficult to find that if we add another potential term, which is similar to the one of form, then in future the other issues also can be handled with the proposed formation scheme.

REFERENCES

[1]. M. Lewis and K.-H. Tan, “High precision formation control of mobile robots using virtual structures,” Autonomous Robots, vol. 4, pp. 387– 403, 1997.

[2]. Q. Jia and G. Li, “Formation control and obstacle avoidance algorithm of multiple autonomous underwater vehicle(AUVs) based on potential function and behavior rules,” in Proceedings of IEEE International Conference on Automation and Logistics, Jinan, China, 2007, pp. 569–573

[3]. .M. Porfiri, D. Roberson, and D. J.Stilwell, “Tracking and formation control of multiple autonomous agents: A two-level consensus approach,”Automatica, vol. 43, pp. 1318–1328, 2007.

[4]. E. Fiorelli, N. E. Leonard, P. Bhatta, D. A. Paley, R. Bachmayer, and D. M. Fratantoni, "Multi-AUV control and adaptive sampling in Monterey Bay," IEEE Journal of Oceanic Engineering, vol. 31, no. 4, pp. 935-948, 2006.

[5]. Huizhen Yang and Fumin Zhang, “Geometric Formation Control for Autonomous Underwater Vehicles”, 2010 IEEE International Conference on Robotics and Automation Anchorage Convention District May 3-8, 2010, Anchorage, Alaska, USA

[6]. C. W. Reynolds, "Flocks, herds, and schools: A distributed behavioural model," in Computer Graphic. (ACM SIGGRAPH'87

Conference Proceeding), vol. 21, 1987, pp. 25-34.

[7]. Fossen, Thor I. “Guidance and Control of Ocean Vehicles”. Wiley,

New York, 1994

[8]. Prestero, Timothy. “Verification of a Six-Degree of Freedom

Simulation Model of REMUS

[9]. Burgard, W., Moors, M., Stachniss, C., & Schneider, F. E. (2005).

Coordinated multi-robot exploration. IEEE Transactions on Robotics,

21(3), 376–386

[10]. R. O.-Saber and R. M. Murray, "Distributed cooperative control of multiple vehicle formations using structural potential functions," Proc. Of 15th IFAC World Congress, Barcelona, Spain, 2002.