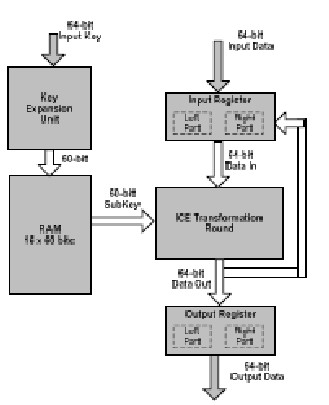
The proposed Feedback Architecture is shown in Fig. 1.
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 884
ISSN 2229-5518
Ambika R1 Sahana Devanathan2
1Associate Professor, 2 Assistant Professor, BMS Institute of Technology, Bangalore-560064
ambika2810@gmail.com ,sahanadev84@gmail.com
Abstract
Cryptography is the art of using mathematics to address the issue of information security. The basic operation in RSA algorit hm is modular exponentiation on large integers, and this operation requires a long computation time. The square and multiply method is the most popular and effective algorithm for computing modular exponentiation . The development of a modular multiplication algorithm suitably mapped to a s ystolic array architecture targeted for implementation in a reconfigurable logic device. The features of the Altera FLEXIKE that makes it mostly suitable to implement the systolic array architecture. This device consists of four types of reconfigurable elements, the logic array blocks (LAB), embed ded array blocks (EAB), the I/O elements (IOE) and the routing resource.
A hardware architecture , for the implementation of the ICE (Information Concealment Engine) encryption algorithm. Since this cipher is optimized for use on software, a hardware implementation of that algorithm that achieves good performance results has much interest. The proposed implementation can be used for both encryption and decryption process. It is a folded architecture using feedback logic, designed for small chip covered area and high speed performance. The proposed architecture was implemented by using an FPGA device. The achieved throughput is equal to 116 Mbit/sec, using a system clock with frequency up to 29.1 MHz.
Index Terms: Cryptography, CPLD, FPGA, ICE, Montgomery algorithm, RSA, security, VLSI.
Among the existing algorithms for public-key
cryptography, the Rivest-Shamir-Adleman (RSA) algorithm
is the best known. Its security lies in the difficulty of the
factorizing large integers [l]. In RSA, a longer key size means better security. Improvements in the factorization algorithm may inadvertently require that the size of the key be continually and appropriately recommended. The
.flexibility to change key length or modify the embedded
algorithm to respond to design flaws or changes in standards or data formats, requires hardware reconfigurability. Reconfigurable hardware applies to a device that can be configured, at run-time, to implement a function as a hardware circuit. Commercially available reconfigurable devices include Field Programmable Gate Arrays (FPGA) and Complex Programmable Logic Devices (CPLD). The basic operation in RSA algorithm is modular exponentiation on large integers, and this operation requires a long computation time. The square and multiply method [7] is the most popular and effective algorithm for computing modular exponentiation. The technique reduces the problem to a series of modular multiplications and squaring steps. Consequently, it is critical that the modular multiplication operation is fast, and Montgomery [2] has proposed a fast method for multiplying two integers modulo M, while avoiding division by M. The idea is transform the integers to M-residues and compute the multiplication with these M-residues. It is then transformed back to the normal representation [5]. Walter [4] then proposed a systolic array architecture for high-speed hardware implementation of the Montgomery algorithm.
This architecture gives a throughput of one digit per clock cycle and a latency of 2m+2, where m is the number of digit in the multiplicand. A. However, this architecture needs several millions of gates for the typical input of 512 bits. An interesting choice is to implement only one row of the architecture to perform single message encryption. This would be realizable in a single IC using today's FPGA technology. In this paper, a systolic array architecture, suitable for reconfigurable logic implementation, of the Montgomery modular multiplication is proposed. This will become the core module in a proposed RSA coprocessor that is implemented in a reconfigurable logic device, the FPGA. This coprocessor will off-load computing-intensive cryptographic operations off a general-purpose processor, such that a high performance system can be obtained. To achieve the required speed-up in the RSA operation a PCI bus interface is employed. The prototype is fabricated in Altera FLEXIOKE series FPGA mounted on a PCI card in a Pentium PC.
Matthew Kwan [2] in order to solve the need for secure encryption algorithms proposed a new algorithm similar to
DES. This algorithm is called ICE, which stands for Information Concealment Engine, and it has the interface of DES thus maintaining full compatibility with that algorithm. It can act as a substitute in existing
applications. It is based on the idea of Data Dependence
Rotation (DDR) since it uses Controlled permutation (CP) in order to maintain its cryptographic security, like] CIKS-1 and SPECTR-H64 algorithms [3, 4]. The ICE algorithm was designed for use in software applications. Those applications however are slow due to the use of modular arithmetic [2]. So the need for faster implementations is
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 885
ISSN 2229-5518
great. That can be achieved through hardware implementations. The ICE algorithm has not been
implemented in hardware so there is a certain interest as to if that is possible and if the results are good enough for the hardware to be usable. Considering the fact that hardware implementations are generally faster and more reliable than software implementations the outcome of a hardware design is even more interesting. An architecture and the VLSI implementation of the ICE encryption algorithm are designed in the following manner. The system operates for the both encryption and decryption processes and has been optimized for low hardware resources and for high–speed performance. The proposed architecture has very encouraging performance result in terms of speed and throughput. This makes the design very useful in current applications that use DES as the base of a cryptographic protocol. With the proposed architecture we focus on proving that the ICE algorithm can easily be implemented in hardware.
The secure transfer and storage of information in the electronic realm has today become critical as the digital world becomes more and more dependent on e-mail, secure telephony, mobile internet, e-commerce, e-banking and so on. Cryptographic systems can provide the objectives of information security: confidentiality, user authentication, data origin authentication, data integrity and non- repudiation . In contrast to symmetric-key cryptosystems, public-key cryptosystems are capable of fulfilling all of these objectives. However, in order to be fast enough and feasibly practical in the applications mentioned above, public-key schemes have to be implemented in hardware. Hardware implementations also provide for ease of installation as well as security from tampering.
Security is a primary requirement of any wireless
cryptographic protocol. In order to find a solution to this always up to date problem, cryptographic algorithms are constructed to provide secure communication applications. However, the clever design of an algorithm is essential if the security of an application is to be maintained. Although there are many good algorithms with different usages and characteristics, not all of them can be characterized fully secure. Many works from different research groups have been published, analyzing cryptographic methods for finding holes in the security strength of today’s encryption algorithm. Thus new encryption algorithms are needed that do not have such security holes. That however might have the side effect of high complexity, which can make the implementation of an algorithm very difficult if not
impossible. One of the major problems of modern computer security is the design of cryptographic algorithms
that have as little vulnerabilities as possible while maintaining their low implementation complexity. Many algorithms that are cryptographically secure are not easily implemented in computer applications especially in hardware. Thus the need for hardware implementations of secure algorithms becomes even greater.
In RSA, to encrypt a message M to its cipher text C, we perform C = XE mod M using the public key E. To restore the message, X = CD mod M is performed, where D is the private key. In general,
n-1
E = Σ ei*2i, ei € (0, l } denotes a
i=0
big integer that consists of n bit in radix-2, ei is the Ch digit.
Modular exponentiation is performed using the square and multiply method as given below. Here, the exponent E is treated bit by bit. Note that the two lines in step 2a are modular multiplications under the same modulus, and they have same multiplier Zi. Since they are independent of each other, they can be executed in parallel. The loop runs for n cycles where n is the number of bit in E. If higher radix is used in E, then the number of digit to represent E and hence the number of iteration is reduced. The drawback of this speedup is that 2k-2 multiple of X have to be precomputed and stored. k is the number of bit used to represent one
digit.
Algorithm 1 : ModExp(X, E, A4)
compute P = XE mod M, E = X-l ei.2i,
ei E { 0 , 1 )
2. For i = 0 to n- 1 Loop
4. i=O
I . Po= I,Z0=X
2a. Ptemp = Pi'Zi mod M
Zi+ = Zlz in od M
2b. If ei 1 Then Pi+, Pt,omp Else Pi+, = Pi
3. End For
The speed of this algorithm relies on the speed of modular multiplication in step 2a.
C = M e mod n (1)
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 886
ISSN 2229-5518
M =C d mod n (2) RSA Key Generation
ICE is a standard Feistel block cipher [2], with a structure similar to DES. It takes a 64-bit plaintext, splits it in two 32- bit halves and mixes them with the key in a fairly simple process. The right half and a 60-bit subkey are fed into the function F. Then the output is XORed with the left part of the key and the halves are swapped.
This is the Transformation Round of the ICE algorithm.
This process is repeated for 16 rounds. However the final round, before the ciphertext production, is different. The final swap is omitted. The decryption process is the same, except that the subkeys are used in reverse order. From the above description of ICE algorithm it is clear that its strength is centred in the F function. In ICE the 32-bit plaintext, using a function E, is expanded in four 10-bit values according to the manner:
E1= P1 P0 P31 P30 P29 P28 P27 P26 P25 P24
E2= P25 P24 P23 P22 P21 P20 P19 P18 P17 P16
E3= P17 P16 P15 P14 P13 P12 P11 P10 P9 P8
E4= P9 P8 P7 P6 P5 P4 P3 P2 P1 P0
One of the differences from DES is that after the expansion
function E, key permutation is used [2]. A 20- bit subkey, called permutation key is used to swap E1
with E3 and E2 with E4. When the odd bits of the permutation key are set they swap E1 relative bits with E3 bits else they swap E2 relative bits with E4 bits. The
outcome is XORed with a 40-bit subkey and the fed in the
S-boxes.
The S-boxes of ICE use Galois Field exponentiation. Each S- box takes a 10-bit input X. Bits X9 and X0 are
concatenated and form the row selector R while bits X8 to
X1 concatenated form the 8-bit column selector C. For each row, there is a XOR offset value OR and a Galois Field prime PR. The output of the S-box is an 8bit value which is given by (C xor OR)7 mod PR . In Table 1 the
values of the XOR offset and the Galois Field primes can be
seen for all four S-boxes.
Field prime values
O0 O1 O2 O3 P0 P1 P2 P3
S1 131 133 155 205 333 313 505 369
S2 204 167 173 65 379 375 319 391
S3 75 46 212 51 361 445 451 397
S4 234 205 46 4 397 425 395 505
The four 8-bit outputs of the S-boxes are combined using a
permutation function P in a 32-bit value which is the result
of the F function .

The proposed Feedback Architecture is shown in Fig. 1.
The proposed Feedback Architecture performs both encryption and decryption with input plaintext block and key vector equal to 64 bits. It uses an input and an output register. Each of them stores the values of the left and right part of every round and swaps the two parts if needed (according to the algorithm in the final round there is no swap). Also a 16x60-bit RAM is needed to load and store the round keys. The Key Expansion Unit creates the round keys, using the 64-bit Input Key following the specifications of ICE. The Keys are stored inside the RAM for every
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 887
ISSN 2229-5518
round. The encryption process is fairly simple. In each clock cycle, the data stored in the input register are inserted
in the ICE Transformation Round along with the subkeys stored in the RAM. This process is repeated for 16 rounds. However at the final round, the Output Register is used in order to swap the left and right part of the ICE Transformation Round Output. That value of the Output Register is the cipher text. The decryption
process follows the same process. However the subkeys are used in reverse order. From the analysis of ICE, it is clearly seen that the main design interest lies in the ICE Transformation round of the algorithm, shown in Figure 2. Especially, in the implementation of the F function. The F function has four parts. The Expansion function E, the key permutation, the S-boxes and the Permutation function P. Key permutation can easily be implemented using two multiplexers 2-1, while the Expansion and Permutation functions are just a rearrangement of wires. So the highest implementation cost of the F function lies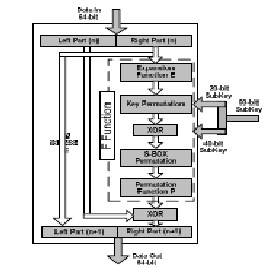
in the design of the S-boxes.
Considering that each S–box uses modular exponentiation in order to calculate its output, a VLSI architecture based on Montgomery Multiplication
algorithm is proposed. This component is specially
designed to do the mathematical function A7mod P. The architecture of this component is pipelined, with 6 stages, and it is based on the following algorithm:
A7mod P (X, P)
1. A=MM(X, R’, P)
2. B=MM(A, A, P)
3. C=MM(B, A, P)
4. D=MM(C, C, P)
5. E=MM(D, A, P)
6. Out=MM(E, 1, P)
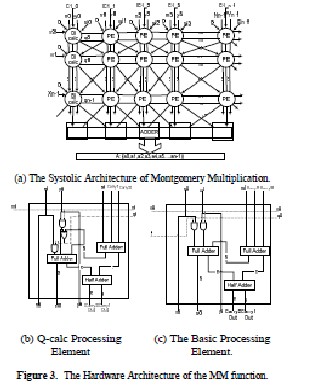
MM is the Montgomery Multiplication function and R’=R2modP is a pre calculated fixed number. Step 1 is needed to transform the input value X into Montgomery format and step 6 to change the Montgomery formatted result E into a normal number value. The Montgomery Multiplication algorithm was implemented using a systolic architecture, shown in Figure 3, based on the following algorithm [5-8]:
1. A=0
2. For k=0 to n-1 do begin
3. q=(a0 +xky0) mod b
4. A=A+xkY+qN
5. A=A/b
6. Return A
This algorithm is a modified version of the original Montgomery multiplication algorithm. The base b is considered Radix 2 (b=2) and R=2n where n is the bit length of the value N. The architecture of the Montgomery multiplication, as seen in Figure 3, is an array of Processing Elements.
The architecture of the Montgomery multiplication, as seen
in Figure 3, is an array of Processing Elements (Figure 3(c)). The elements on the first row, however, have a XOR gate more than the basic Elements PE. This gate is used for the calculation of the q value. Those elements are called Q-calc Processing Elements (Figure 3(b)). The output of the array is produced in a Carry
Save format so an adder is needed in order to get the final
result. For that function an adder was implemented using
Carry look ahead logic.
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 4, April-2013 888
ISSN 2229-5518
We have compared RSA cryptography, ICE encryption algorithm.
The modular exponentiation operation is the core of the RSA algorithm that has become the most widely used public key computer security algorithm. New architectures for the implementation of Montgomery modular exponentiation for RSA have been proposed. The new architectures use a modified Montgomery algorithm in which the operations of modular multiplication and modular reduction are carried out separately but in a parallel way.
ICE is a symmetric key block cipher specially designed
for software applications. It is designed for high clock speed – performance and minimized area resources.
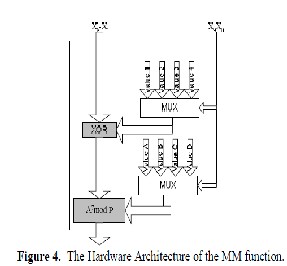
The input X of the S-box is XORed with the appropriate value from Table 1. The output is fed to the A7mod P function where P is the value taken from Table 1. The appropriate values for the S-box are chosen from X9X0 bits of the input using multiplexers 4-1. The result of the A7mod P function is the output of the S-box. The structure
[1] SCHNEIER, B., 1996. Applied Cryptography: Protocols, Algorithms, and Source Code in C, John Wiley & Sons.
[2] A. P. Fournaris, N. Sklavos and O. Koufopavlou
VLSI architecture and FPGA implementation of ICE encryption algorithm.
[3]Deng Y., Mao Z., and Ye Y.,. 1998. Implementation of RSA Crypto- Processor Based on Montgomery Algorithm.
[3] Zhang. C.N, Xu. Y and Wu. C., 1997. A Bit-Serial Systolic
Algorithm and VLSI Implementation for RSA.
[4] Hinek. M., 2010. Cryptanalysis of RSA and Its Variants.
[5] Rivest, R., Shamir, A., and Adleman, L, 1978. A Method for Obtaining Digital Signatures and Public Key Cryptosystems. Communications of the ACM.
of | an | S-box | is | shown | in | Figure | 4. | [6] Stallings W.2003, Cryptography and Network Security:Principles and Practices. |
[7] Burnett S. and Paine S, 2001. RSA Security’s Official | ||||||||
Guide to Cryptography. McGraw-Hill. | ||||||||
[8] Ashenden P. and Lewis J, 2006. The Designer’s Guide to VHDL. | ||||||||
Morgan Kaufmann Publishers. | ||||||||
[9] Hwang E. Digital Logic and Microprocessor Design with VHDL. |
IJSER © 2013