International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 769

ISSN 2229-5518

Dynamic Analysis of Marine Cable

Rajesh Mondal*

Abstract— This paper will focus on a dynamics analysis of a marine cables which are mainly used in offshore and subsea applications (i.e. Mooring Line, Riser, ROV umbillicals, pipeline etc). We considered an Euler Bernoulli beam cable model which is derived based on Newton’s second law of motions and beam cable equilibrium conditions in continuous system. Different beam cable model and end conditions are adapted to recognize our physical problems and also boundary conditions, assumptions are adjusted to obtain solutions. The models are solved both mathematically and numerically. We estimated structural reliable parameters like displacement, natural frequency, damping etc and it is visualized graphically.

Index Terms— Continious System, Euler Bernoulli beam cable model, Mathieu Equation, Cable frequenciy and response, Parametric model.

——————————  ——————————

1. INTRODUCTION

HE dynamic model of the offshore and subsea cable structure discussed have involved only finite number of independent coordinates and ordinary differential
equations of motion. In the single degree of freedom sys- tems, one coordinate is chosen to describe the dominant structural vibration mode in the plane. In the multi-degree of freedom systems, examples included the rigid gravity
platform with coordinates to describe sliding and rocking
motion and jacket template platforms with coordinates to
describe the motion of discrete masses lumped at node
points.
For line components such as rather long beam, mooring,
riser, pipelines, umbillicals and cables, alternative continu-
ous system models may provide more precise and some-
times more economical descriptions of component motion
[1]. Since partial differential equation is used to character-
ize the motion of a continuous line component, solutions
are generally more involved mathematically than for a cor-
responding lumped system. However, if the continuous models are chosen judiciously, closed form expressions can
be derived for the characteristic frequenscies and mode shapes of line components, which then lead to upper and lower bounds on their dynamic responses.

————————————————

• *Author Rajesh Mondal, Assistant Professor is currently working at department of Naval Architecture and Offshore Engineering in AMET University, India, PH-+91-8807181618. E-mail: rajeshmondl@gmail.com

One special class of continuous line components are analyzed in this paper. The structural component consid- ered here is the cable which resists tension but whose bend- ing stiffness is negligible.

2. GOVERNING EQUATIONS

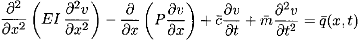
The general form the linear Bernoulli-Euler dynamic beam cable equation is derived [1] [2].
---------------
------- (1)
Where EI, P, and 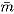are arbitrary functions of x and exci- tation load is arbitrary in both х and t.
Cable Frequencies and Mode shape:
For undamped, flexible cable (EI =0), a subjected to ten- sion load P which is independently of x and equation (1) becomes,

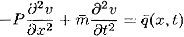----------------- (2) Consider the free, undamped vibrations of a flexible cable of constant m and constant tension P= P. The corresponding equation of motion is deduced as,

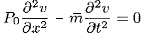----------------------- (3) The cable frequencies are given by,

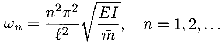---------------- (4)

International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 770

ISSN 2229-5518

And corresponding mode shape is given by,

Cable Response (Parametric excitation):
-------- (5)

Cable response due to longitudinal or parametric end exci- tation may occur vertical lines or chain when the ship or buoy undergoes heave motion in regular wave.
---------------- (6) The analytical result of the equation (6) can be expressed interm of Mathieu equation which is [4],

----------------------- (7)

3. WORKED EXAMPLE

This worked example illustrates the mode shape and fre- quencies of the undamped, free vibration frequencies for a submerged floating marine structure where Riser is con- nected with BOP or Mooring line is fixed at seabed in fig. a, offshore jacket, jack up, articulated tower platform end of brace is welded to a leg, the ends are not simple sup- ports, but because of leg and joints flexibility, these end are not fully clamped either fig. c, floating pipe line for of- floading oil gas to supply vessel or floating water supply

Fig. 2 The first three mode shape for free- free elastic beam cable

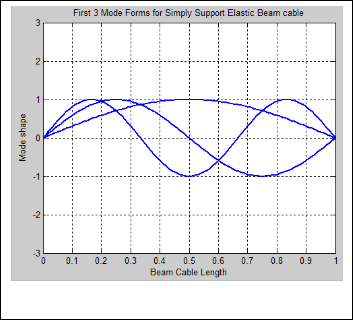
Fig. 3 The first three mode shape for fixed fixed elastic beam cable

pipeline in fig. b, ROV cable fixed with manned struc- ture and other end connected with unmanned vehicle in fig.c which may be considered as free end or pipeline seg- ment during deployment in fig. d, etc beam cable end mod- els has shown in TABLE 2.

Fig. 1 The first three mode shape for a simply supported beam cable

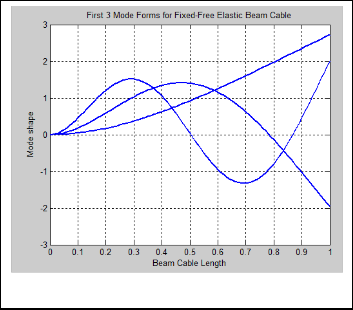
We implemented the above mathematical formulation in- to Matlab to visualize the mode shape and their respective frequencies for different end conditions of beam are given in TABLE 1. We used number of mode equal to 3 and beam cable length in meter. This mathematical model predicts that increasing frequencies are possible as number of mode becomes larger and larger.

International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 771

ISSN 2229-5518

Fig. 4 The first three mode shape for fixed free elastic beam cable

To illustrate cable response due to longitudinal or para- metric excitation of mainly taut mooring system, drilling riser system or tension leg tethers can be considered has shown in Table 2. This type of excitation may occur in ver- tical lines when the ship, buoy or platform undergoes heave motion in regular waves.
Parametric oscillator for equation (7) is solved numerically
for time history. The equation can be time integrated using methods like Euler-method, Runge-Kutta method using initial boundary values. Runge-Method is the most accurate method.
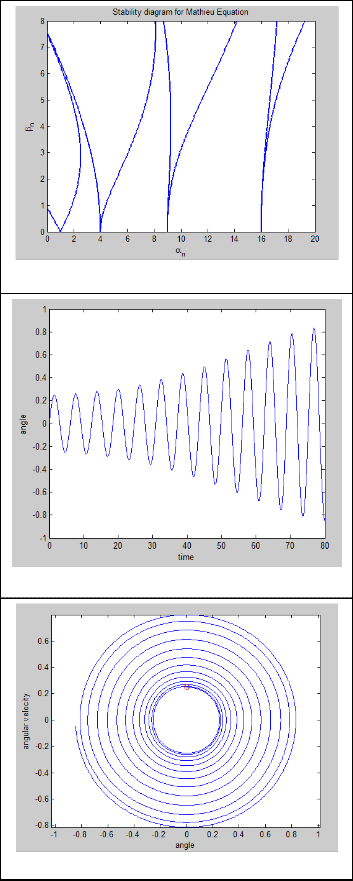
From figure 7 and 8, it is clear that the amplitude of the oscillation keeps on increasing exponential, showing the instability. The plot shows that the solution moves away from the stable point. This instability is due to a phenome- non called parametric resonance. Parametric resonance takes place when the external excitation frequency ap- proaches integral multiple of the systems natural frequency. This is a nonlinear resonance phenonmenon. In most of the cases this parametric resonance is catastrophic. This insta- bility will not be affected by damping as well. Damping only may reduce the rate of increase of amplitude.
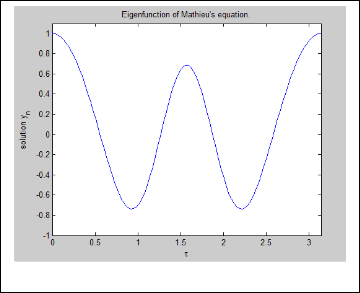
The solution of Mathieu equations is given figure 6.
If lies in between the curve area regions, then 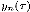is stable, but is this parameter set is elsewhere, the respons- es are unstable.
We compared our result with Haines-Stability plot in reference [5] which is same as our stability diagram shown in figure 6. It is also clear the oscillator oscillates indefi- nitely, with large oscillator showing beating like behavior between the natural frequency of cable and external fre-

TABLE 1

CABLE BEAM FREQUENCIES (RAD/SEC)

quency. In the figure 5, 7 and 8 we have shown behavior of the oscillator without damping and this position of this point in the stability diagram in figure 6. It must be in the unstable region.

Fig. 5 stable or bounded response of cable

International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 772

ISSN 2229-5518

TABLE2

BEAM CABLE END CONDITIONS

Fig. a Both ends simply supported beam cable model

Fig. b.Free free elastic beam cable model

Fig. c. Fixed fixed beam cable model

Fig. d. Fixed free beam cable model

International Journal of Scientific & Engineering Research, Volume 5, Issue 3, March-2014 773

ISSN 2229-5518

4 CONCLUSION

Fig.6 Stability diagram for Mathieu Equation

Fig. 7 Unstable or unbounded response

The purpose of the dynamic analysis of cable is to represent a reliable and safe structure in marine applications. This paper has presented cable mode shape, frequencies and re- sponse which may be a good result in reality. But we need to calculate number of modes to obtain upper limit. Also in stability diagram of cable and instability phase diagram can explain the reliable safe design parameters. We used Mathieu model for response cable response estimation and this model is able to explain nonlinear effect of parametric model but it is not exactly explained the behavior of cable in random motion as we considered as a regular heave mo- tion. But marine cable analysis may be difficult for sever environmental condition which will predict the actual max- imum limit. Therefore, the model we have presented in this paper is not able to explain the random phenomenon and random behaviors of cable which we physically expect all the time. We are also looking in our next paper to focus on stochastic analysis of dynamical cables.

REFERENCES

[1] James F. Wilson, “Dynamics of offshore structure”, Published by John Wiley & Sons, Inc.
[2] S.P. Timoshenko, D.H. Young, “Elements of Strength of Materials” Litton Educational Publishing, Inc.
[3] Clough, R.W., and Penzien, J., Dynamics of structure, second ed., McGraw-Hill, New York, 1993.
[4] Trogdon, S. A., Wilson, J.F., and Munson, B.R., Dyn- maic of Flexible Cables under Combinaed Vortex and Parametric Ecitation, Journal of Dynamic Systems, Mesurement and Control, 1976.
[5] Lubkins, I., and Stokes, J.J., Stability of Columns and
Strings under Periodic Forces, Quality of Applied
Mathematices, 1(1), 1983.

Fig. 8 Unstable or unbounded response