Here α and β are two complex numbers representing amplitude of states 0 and 1. The continuous nature of qubit coefficients enable infinite storage capacity of quantum ele- ments. α and β are related to each other by following equation.
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 196
ISSN 2229-5518
Design of High Speed 32-bit Microarchitecture for
Emulation of Quantum Computing Algorithms
Mayuresh Deshpande, Hardik Shah, Vinayak Kini, Chirag Bafna
—————————— ——————————
ver the past few years, Quantum computing has proved to offer a paradigm shift in the field of computing owing to its ability to tap in the fundamental fabric of reality.
Quantum computer is a computation system which makes use of the properties of quantum mechanics for performing vari- ous operations on data. Some of the fundamental properties used in quantum computing are superposition, entanglement and quantum tunneling. It leads to the non-deterministic or probabilistic computation of data. Therefore quantum com- puters outperform classical computers in the fields of data search and encryption.
However, practical implementation of quantum com- puter has always been a challenging task for the electronics community. The daunting task in the quantum computation is to deal with the quantum states. Quantum states unlike classi- cal states, exhibit superposition of states and are expressed in probabilistic terms using quantum bits widely known as qubits. Quantum processor based on few qubits have been demonstrated using nuclear magnetic resonance[4], cold ion trap[4], optical systems[4] and superconducting circuits[3]. We are still years away from developing a solid state quantum computer[1]. We know that we cannot increase computing power indefinitely because as conventional semiconductors get smaller and smaller they are going to hit a barrier within next ten years or so where they will no longer work as they do today. It will be no longer possible to scale semiconductor de- vices to smaller scales than now and that is where quantum computers are one possible solution to that problem.
The another way of harnessing benefits of quantum computing is emulating quantum algorithms on classical sys- tems to improve their performance. In 1982 Feynman's pio- neering paper on quantum computing was the first to indicate such possibility. Many attempts have been made in the last two decades to emulate quantum algorithms on software and hardware. Software emulators[5] employ explicitly defined quantum libraries to facilitate implementation of quantum algorithms. Emulation of few search and factoring algorithms have been demonstrated using software emulation[5]. How-
ever present day processors[5] are unable to cope up with immense parallelism required by quantum computing.
This project is centred around the development of high speed 32 bit special purpose processor capable of han- dling quantum computing more efficiently than present day systems. The processor is supposed to provide specific instruc- tion set in order to support basic quantum operations with ease. The qubits are represented in 32 bit IEEE floating point format for high precision computation. The present state of qubits is stored in array of 32 bit registers. The memory organ- ization of the current design supports N-qubit operations with higher efficiency. All the operations on the data are carried out in the execution unit which is called as Quantum Computing Unit.
The Quantum Computing Unit (QCU) is at the heart of the design and it incorporates superscalar architecture hence enabling parallel computation. The architecture em- ploys 32 bit floating point unit to enable high speed multipli- cation and addition. The striking feature of the processor is its ability to eliminate redundant multiplications thereby demon- strating higher performance then other emulating models[9] of quantum algorithms. This is achieved by replacing complex operation of matrix multiplication by selective multiplication of quantum states depending on the quantum transform[7]. The QCU also enables entanglement of 2 distinct qubits at a time. However it can operate on previously entangled quan- tum data with higher efficiency. The proposed microarchitec- ture provides ideal emulation platform for quantum algo- rithms and presents a way to tap in the infinite computing power of quantum mechanics.
————————————————
• Authors are affiliated with Vivekanand Education Society's Institute of
Technology, Chembur, Mumbai-74.
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 197
ISSN 2229-5518
The major difference between quantum computing and classi- cal computing arises from the types of values required to per- form computing. While the basic information units for classi- cal circuits are 0 and 1, quantum computing uses probabilistic numbers as bearers of information[8]. Hence, representing a single quantum information unit might require a large num- ber of classical bits, depending on the precision required. In this case 32 bit floating point numbers[9] are used for repre- senting basic quantum information.
Quantum bits also known as qubits are the fundamental units of quantum computing. A single qubit is represented as su- perposition of two states '0' and '1' with corresponding ampli- tudes denoted by 'α' and 'β'.![]()
Here α and β are two complex numbers representing amplitude of states 0 and 1. The continuous nature of qubit coefficients enable infinite storage capacity of quantum ele- ments. α and β are related to each other by following equation.
|α|2 + |β|2 = 1
The superposition phenomena, by which the qubits simultaneously exist in states![]() is explained by con- sidering |α|2 and |β|2 as probabilities of being in states
is explained by con- sidering |α|2 and |β|2 as probabilities of being in states![]() respectively.
respectively.
Quantum entanglement is a phenomenon in which two qubits interact in such a way that the state of each qubit cannot be defined independently. Hence these two qubits are required to be represented in the entangled state. There are certain quan- tum circuits which produce entangled output of the qubits at input. Quantum entanglement is very important operation required for quantum cryptography. The entanglement of two qubits is shown below.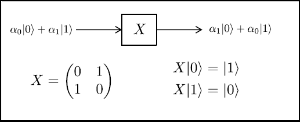
quantum computing. In this operation, the coefficients of states ![]() are interchanged. The representation of bit- flip gate and matrix equation is shown in figure 1.
are interchanged. The representation of bit- flip gate and matrix equation is shown in figure 1.
Fig.1 : Bit-Flip Gate
Phase Shift gate also known as Z gate operates on a single qubit and alters the sign of the second coefficient. The opera- tion of the same is shown in figure 2.
Fig.2: Phase Shift Gate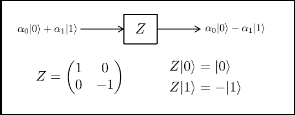
Hadamard gate is one of the most commonly used quantum gate and it corresponds to one qubit rotation. The hadamard gate can be implemented for multiple qubits. It involves 2 x 2 matrix multiplication with current quantum state. The matrix of the hadamard transform can be represented as below.
H = ![]()
Figure 3 shows representation and equation of hadamard gate for single qubit.![]()
![]()
![]()
Basic quantum operations performed on qubits to generate new quantum state. In quantum circuits, quantum operations are performed by quantum gates. Fundamental quantum gates which operate on a single qubit are as follow.
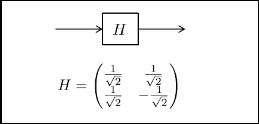
Fig. 3: Hadamard Gate
Bit flip gate also known as X gate functions as not gate in
C-NOT gate acts on two or more qubits and performs con- trolled NOT operation of second qubit depending on 1st qubit.
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 198
ISSN 2229-5518
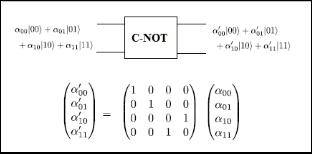
The output of the C-NOT gate is an entangled quantum state. It requires four complex multiplications for two qubits. The representation and matrix equation for two qubit C-NOT gate is shown in figure 4.
Fig. 4: C-NOT Gate
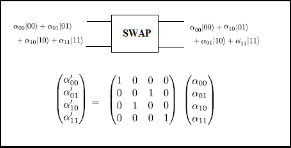
As its name suggests, Swap Gate is used for swapping two qubits. In Swap gate the entanglement of the qubits is pre- served and the coefficients for states are changed The equation for the same is shown in the figure 5.
fied format signed exponent field is used to enable representa- tion of small numbers.![]()
αreal
S Se Exp. (7 bit) Mantissa (24 bit)![]()
αimag
S Se Exp. (7 bit) Mantissa (24 bit)![]()
βreal
S Se Exp. (7 bit) Mantissa (24 bit)![]()
βimag
S Se Exp. (7 bit) Mantissa (24 bit)
![]()
Entanglement of two qubits is shown below. It is represented using 4 complex coefficients i.e. eight 32 bit floating point numbers.
Fig. 5: SWAP Gate
Quantum bits are represented as superposition of two states '0' and '1' with corresponding amplitudes denoted by complex numbers 'α' and 'β'.
follow.
Representation of Entanglement of two qubits is as![]()
real
Imag
![]()
real
Imag
![]()
real
Imag
![]()
real
Imag
![]()
Hence each qubit is represented by four 32 bit floating point numbers as follow. Use of modified IEEE 754 floating point format in this case increases precision of the system and also accelerates multiplication of two numbers. In the modi-
The Quantum Computing Unit (QCU) is a High performance
Parallel Computing Device incorporating superscalar architec-
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 199
ISSN 2229-5518
ture. The QCU is the heart of the entire design and performs functions similar to that of ALU in classical processors.
The said QCU is capable of carrying out basic quan- tum operations on input qubits. The operations performed by the QCU include Single qubit Bit-flip, Phase shift and Hada- mard transform. It can also operate on entangled qubits and perform operations corresponding to Swap and C-NOT quan- tum gates.
The QCU incorporates superscalar architecture in or- der to enable parallel computation of quantum transforms. QCU can operate on two single qubits simultaneously de- pending on the control signal provided to it. Apart from basic quantum transforms, QCU can perform entanglement of two qubits or operate on two entangled qubits simultaneously.
32 bit complex floating point unit is the most funda- mental block of the QCU architecture. It is required to carry out the multiplication and addition of coefficients of quantum states in the qubit [10]. Complex FPU employs 32 bit floating point addition and multiplication hardware and provides re- sult in the complex number format.
The hardware required to carry out different opera- tions involving quantum operands is shown in the table 1.
TABLE 1
HARDWARE REQUIREMENT OF QUANTUM COMPUTING UNIT

Fig 6: Architecture of Quantum Computing Unit
![]()
![]()
The operation of single qubit quantum gate can be represented = ![]()
![]()
by following matrix equation. Let inital qubit be and final
output be . If ![]()
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 200
![]()
ISSN 2229-5518
![]()
then![]()
![]()
![]()
Therefore one can conclude that and
Hence computation of ![]() ' comprises of 4 com-
' comprises of 4 com-
plex multiplications and two complex additions.
The architecture for the general quantum gate con-
sists of 4 complex number floating point multipliers operating
parallel and two complex number adders. The diagram of ar-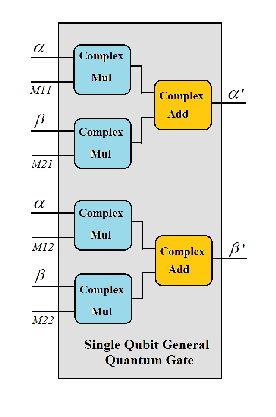
chitecture is shown in the figure 8.
Fig. 8: Architecture of general Quantum Gate
As mentioned previously, the QCU is also capable of perform- ing quantum entanglement of two qubit system at a time. Therefore it consists of an independent quantum entangle- ment unit performing at high speed.
The equation for the quantum entanglement of two qubits is shown below.
Let
![]()
Hence, we can conclude,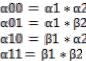
The architecture of Entanglement unit performing above operation is shown in the figure 9.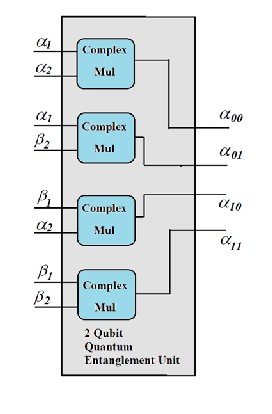
Fig. 9: Architecture of 2-Qubit Entanglement Unit![]()
![]()
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 201
ISSN 2229-5518
The Quantum computing unit consists of two general quan- tum gates working simultaneously, auxiliary Entanglement unit and operation selection logic.
The operation carried out by QCU is determined by control signal generated by processor during decoding of in- struction. The data of quantum state fetched from the register memory is applied to either general quantum gate or entan- glement unit depending on the operation. The result of the QCU is 4 complex quantum coefficients which are forwarded to the memory for write-back operation.
In the schematic of QCU, it can be seen that it oper- ates on 256 bit data bus. Input to the QCU are coefficients of two different qubits. These coefficients are then applied to the parallel quantum gates for quantum operations.
The transform operation performed on the qubit is determined by the matrix coefficients which are applied to the q-gate via select logic depending on the control signal. QCU can perform two quantum operations simultaneously because of two independently functioning quantum gates.
Quantum entanglement in the QCU has independent block functioning on the same inputs as that of q-gates. The result of both q-gates and entanglement unit are applied to the multiplexer which selects one output according to the QCU control signal.
Thus the proposed QCU operates on 256 bit data simultaneously and it is powered by parallel functioning of multiple 32-bit FPUs. Hence it plays key role in the superior performance of the designed processor. The schematic of quantum computing unit is shown in the figure 10.
Fig. 10: Architecture schematic of QCU
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 202
ISSN 2229-5518
The architecture of the processor follows the convention of classical processors. The processor architecture developed for quantum operations consists of 4 stages in its instruction cycle. The operation of the processor along with the archi- tecture schematic is given below.
This stage consists of program counter and the instruction memory. The program counter keeps track of the current instruction address and computes the next address on each clock cycle. During computation, the processor fetches two single qubit instructions in each cycle.
The instructions of the processor will be distin- guished in two types. First type is configuration instruc- tions. These instructions will be required for initializing the data in the quantum state registers for required operation. Second type of instructions is computing instructions. These instructions will specify operations to be performed and the operands required.
In this stage, Instruction is decoded and the control signals for the execution stage are generated. The control signals determine the operation performed by the Quantum Com- puting unit (QCU) in the execution stage.
This stage also consists of Quantum state memory which holds the values of coefficients of different qubits on which the operation is to be performed. Depending on the address specified by the address field in the instruction, qubits are fetched and forwarded to the QCU.
Execution unit is the heart of the processor architecture and it consists of superscalar Quantum Computing Unit consist- ing of multiple FPU operating in parallel mode. The de- tailed description of the QCU is given in the section 5.
The result obtained by the QCU is written back in the quan- tum state registers in order to update the qubits. The write operation of registers is carried out on different clock edge than that of read operation to avoid data hazards.
The State transitions of the proposed processor while executing quantum instruction are similar to that of single cycle classical processor. The state diagram is shown in figure 11.
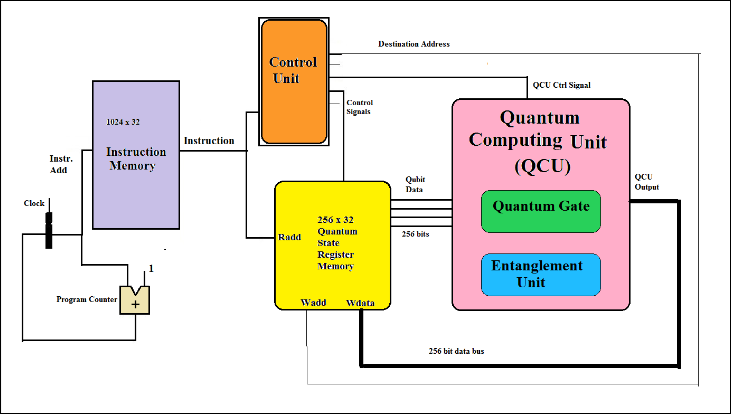
Figure 12 shows the combined data-path of the processor.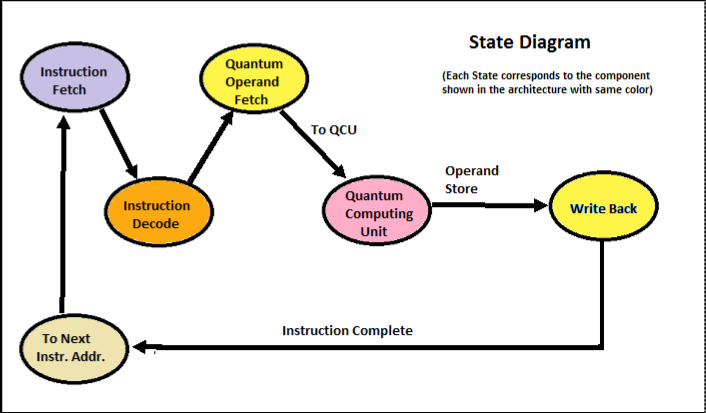
Fig.11:State transitions of the processor while performing quantum operation
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 203
ISSN 2229-5518
Fig.12 Processor Datapath
The quantum computing unit incorporated in processor can be used to perform Quantum Fourier transform and also in Grover's algorithm which is a quantum search algorithm that runs quadratically faster than any equivalent classical algorithm. The Instruction set architecture for the proposed microarchitecture will be developed to support complex instructions executing various quantum operations in dif- ferent algorithms.
Various real-world applications of the quantum computing systems are as follow:
1. Quantum computing can play a significant role as an HPC (high performance computing) system, wherein it can be used as to optimize system goals within very less time.
2. Quantum computers can be used to simulate and predict folding patterns of proteins which can transform our understanding of complex biological systems.
3. Quantum computing algorithms can be incorporated in efficient transportation system so that sophisticat ed analysis of traffic patterns in air and ground will forestall bottlenecks and snarls.
4. Quantum computers will be able to analyze the vast amount of data collected by telescopes and con tribute to the space exploration.
The goal of this project was to develop an architecture ca- pable of emulating Quantum Computing operations at high speed. The proposed design of Quantum Computing Unit increases the computation speed manifold owing to its par- allel architecture. The representation of quantum data in 32 bit floating point format improves the precision and accu- racy of the computation. Hardware requirement of such architecture is considerably large. However, it is far more superior than existing emulation systems of Quantum algo- rithms and it can be optimized during implementation phase. The architecture of the entire processor is planned to be implemented in Verilog and FPGA [10] with the help of HDL tools such as Xilinx 12.1. The prototype of Quantum emulation microarchitecture presented in this paper will certainly open further avenues in the practical implementa- tion of quantum computing.
Authors would like to express their gratitude towards V.E.S Institute of Technology, Chembur, Mumbai; for providing necessary resources to conduct research and ex- perimentation related to this project.
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 204
ISSN 2229-5518
[1] Han, J.; Jonker, Pieter, "On quantum computing with macroscopic Josephson qubits," Nanotechnology, 2002. IEEE-NANO 2002. Proceedings of the 2002 2nd IEEE Conference on , vol. 305, no. 308, pp.2002.
doi: 10.1109/NANO.2002.1032252G.
[2] Z. Zilic and K.Radecka, The Role of Super-fast Transforms in speeding up Quantum Computations, Proceedings of the 32nd Internatitonal Symposium on Multiple-Valued Logic (ISMVL02), 2002I. S.
[3] Jonker, Pieter; Han, J., "On quantum and classical computing with arrays of superconducting persistent current qubits," Computer Architectures for Machine Perception, 2000. Proceedings. Fifth IEEE International Workshop on ,vol. 69,no. 78,pp. 2000. doi: 10.1109/CAMP.2000.875960.
[4] DiCarlo, L.; Chow, J.; Gambetta, J.; Bishop, L.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.; Schoelkopf, R., "Demonstration of two- qubit quantum algorithms with a solid-state electronic processor," Lasers and Electro-Optics, 2009 and 2009 Conference on Quantum electronics and Laser Science Conference. CLEO/QELS 2009. Conference on , vol. 1, no. 1, pp. 2-4. June 2009.
[5] ”Libquantum”, Online Quantum Library Documentation, http://www.enyo.de/libquantum/Electronic Publication: Digital Object Identifiers (DOIs):
[6] M. Steffen, L. M. K. Vandersypen and I.L. Chuang, Toward Quantum Computation: A Five-Qubit Quantum Processor, IEEE Micro, Vol. 27, No. 1, pp. 24-34, 2001.
[7] H. Goto, Y. Hasegawa, and M. Tanaka, “Efficient Scheduling Focusing on the Duality of MPL Representatives,” Proc. IEEE Symp. Computational Intelligence in Scheduling (SCIS 07), IEEE Press, Dec. 2007, pp. 57-64, doi:10.1109/SCIS.2007.357670.
[8] J.P. Hayes and I.L. Markov, Simulation, Synthesis and Testing of Quantum Circuits, DARPA QuIST annual research review, Beverly Hills, CA, June 2003.
[9] Montoye, R.K.; Hokenek, E.; Runyon, S.L., "Design of the IBM RISC System/6000 floating-point execution unit," IBM Journal of Research and Development , vol. 34, no. 1,pp.59,70, Jan. 1990 doi: 10.1147/rd.341.0059.
[10] Khalid, A.U.; Zilic, Z.; Radecka, K., "FPGA emulation of quantum circuits," Computer Design: VLSI in Computers and Processors, 2004. ICCD 2004. Proceedings. IEEE International Conference on , vol. 310, no. 315, pp. 11-13. Oct. 2004.
doi: 10.1109/ICCD.2004.1347938
IJSER © 2015 http://www.ijser.org