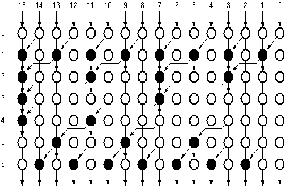International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 1502

ISSN 2229-5518

Design and Characterization of Koggestone, Sparse Koggestone, Spanning tree and Brentkung Adders

V. Krishna Kumari, Y. Sri Chakrapani, Dr. M. Kamaraju

Abstract-- In various VLSI designs, the adders are frequently used. The most commonly used adder is the Ripple Carry Adder (RCA), which can be implemented by using half adders and full adders.This RCA is a serial adder which is used to perform any number of additions, but it has propagation delay problem due to carry propagation from stage to stage which leads to more delay. To overcome this delay, parallel adders (parallel prefix adders) are preferred as they pre-compute the carry. The parallel prefix adders are KS adder (kogge-stone), SKS adder (sparse kogge-stone), Spanning tree and Brentkung adders. These adders are designed and compared by using power and delay constraints. Simulation and Synthesis process is performed on these adders using by Model sim6.4b, Xilinx ISE9.2i.

Keywords—Adders, KS adder, RCA, Simulation, SKS adder, Synthesis.

——————————  ——————————
Ripple carry adder is the cascade of full adders which
performs the addition operation but the only drawback is

I. INTRODUCTION

In processors (DSP) and microprocessor data path units, adder is an important element. As such, extensive research continues to be focused on improving the power-delay performance of the adder. In VLSI implementations, parallel adders are known to have the best performance. Reconfigurable logic like Field Programmable Gate Arrays (FPGAs) has been gaining more popularity in recent years because it offers improved performance in terms of speed and power over DSP-based and microprocessor-based solutions, for many practical designs involving mobile DSP and telecommunications applications and a significant reduction in development time and cost over Application Specific Integrated Circuit (ASIC) designs. The power advantage is important with the growing popularity of mobile and portable electronics, which make extensive use of DSP functions. However, because of the structure of the configurable logic and routing resources in FPGAs, parallel-prefix adders will have a different performance than VLSI implementations [1]. In particular, most modern FPGAs employ a fast-carry chain which optimizes the carry path for the simple Ripple Carry Adder (RCA).

• V.Krishna Kumari is currently pursuing M.Tech, Embedded systems

in department of electronics and communication engineering in JNTUK University, India, PH-9032247973. E-mail: kkecm@yahoo.com

• Y.Sri Chakrapani is currently working as Associate Professor in department of electronics and communication engineering,Gudlavalleru engineering College ,E-mail: srichakrapani@gmail.com

• Dr. M.Kamaraju is currently working as Pprofessor & HOD in

electronics and communication engineering ,Gudlavalleru engineering

College , E-mail:madduraju@yahoo.com
propagation delay as the carry has to ripple from stage to stage. So in order to reduce this delay many adders came into existence. Some of them are Carry skip and Carry look ahead adders which reduce the delay by precomputing the carry. Later Parallel Prefix adders are preferred in order to reduce the delay as they will perform pre-computation and post- computation. In this paper, some of the tree based adder structures are characterized and compared with the Ripple Carry Adder (RCA) and the Carry Skip Adder (CSA). Finally, some conclusions and suggestions for improving FPGA designs to enable better tree-based adder performance are given to meet the present day constraints to reduce the delay and speed up the computation.

II. CARRY-TREE ADDER DESIGNS

Parallel-prefix adders are also known as carry-tree adders. They pre-compute the propagate and generate signals. These signals are variously combined using the fundamental carry operator (fco)[2].
(gL, pL) ο (gR, pR) = (gL + pL•gR, pL•pR) (1)
These operators can be combined in different ways to form various adder structures by the associative property of the fco,. For, example the four-bit carry-look ahead (CLA) generator is given by:
c4 = (g4, p4) ο [ (g3, p3) ο [(g1, p1) ο (g2, p2)] ] (2)
A simple rearrangement of the order of operations allows parallel operation, which results in a most efficient tree structure for this four bit example:
c4 = [(g4, p4) ο (g3, p3)] ο [(g2, p2 ) ο (g1, p1)] (3)
It is readily apparent that a key advantage of the tree- structured adder is that the critical path due to the carry delay is on the order of log 2N for an N-bit wide adder. Various

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 1503

ISSN 2229-5518

families of adders arise from the arrangement of the prefix network. For this study, the focus is on the Kogge-Stone adder , known for having minimal logic depth and fanout (see Fig 1(a)). Here we designate BC as the black cell which generates the ordered pair in equation (1); the gray cell (GC) generates the left signal only. The interconnect area is known

to be high, but for an FPGA with large routing overhead to begin with, this is not as important as in a VLSI implementation. The regularity of the Kogge Stone prefix tree network has built in redundancy which has implications for fault-tolerant designs. The sparse Kogge-Stone adder, shown in Fig 1(b), is also studied. This hybrid design fulfills the summation process with a 4 bit RCA allowing the carry prefix network to be simplified[3].The dark shaded square box is considered as black and node and the dotted square box is considered as gray node of parallel adder.
(a)
This usage of a fast carry-chain for the RCA in FPGA, it is interesting to compare the performance of this adder with the Sparse Kogge -Stone and regular Kogge-Stone adders.

15 14 13

12 11 10 9 8 7

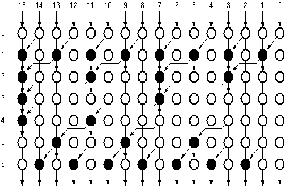
6 5 4 3 2 1 0

15:14 14:13 13:12 12:11 11:10 10:9

9:8

8:7

7:6

6:5

5:4

4:3

3:2

2:1

1:0

15:12 14:11 13:10

15:8 14:7 13:6

12:9 11:8 10:7

12:5 11:4 10:3

9:6

9:2

8:5

8:1

7:4

7:0

6:3

6:0

5:2

5:0

4:1

4:0

3:0

2:0

15:0 14:0 13:0 12:0 11:0 10:0 9:0 8:0 7:0 6:0 5:0 4:0 3:0 2:0 1:0 0:0

(a)
(b)
Fig. 1. (a) 16 bit Kogge-Stone adder and (b) Sparse 16-bit
Kogge-Stone adder
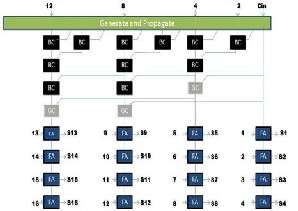
Another carry-tree adder known as the spanning tree and brent kung adders as shown in Fig 2(a) and Fig 2(b) are examined.
(b)
Fig. 2. (a)Spanning Tree Carry Look ahead Adder (16 bit) (b)
16 bit Brent Kung adder.

III. RELATED WORK

On the Xilinx 4000 series FPGAs, the ripple carry adder and carry-skip adders, only an optimized form of the carry-skip adder performance is more better than the ripple carry adder when the adder operands were above 56 bits [4]. A study of adders yielded similar results when implemented on the Xilinx Virtex II. In the authors considered several parallel prefix adders implemented on a Xilinx Virtex 5 FPGA. It is found that the normal RCA adder is superior to the parallel prefix designs because the RCA can take advantage of the fast carry chain
This study focuses on carry-tree adders implemented on a
FPGA of Xilinx Spartan 3E. The distinctive contributions of
this paper are two-folded. In the first, we consider tree-based
adders and a hybrid form which combines a tree structure with a ripple-carry design. The Kogge-Stone adder is taken as a representative of the former type and the sparse Kogge- Stone and spanning tree adder are representative of the latter category[5]. Second, this paper considers the practical issues involved in testing the adders and provides actual measurement data to compare with simulation results. The previous works mentioned above all rely upon the synthesis reports from the FPGA place and route software for their

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 1504

ISSN 2229-5518

results. In addition with being able to compare the simulation data with measured data using a high-speed logic analyzer, our results present a different perspective in terms of both results and types of adders.
The adders to be studied were designed with varied bit
widths up to 128 bits and coded in VHDL. The functionality of
the designs was verified via simulation with Model Sim 6.4b.
The Xilinx ISE 10.1i software was used to synthesize the
designs onto the Spartan 3E FPGA. In order to effectively test for the critical delay, two steps can be taken. First, a memory block (labeled as ROM in the figure below) can be instantiated on the FPGA using the Core Generator to allow arbitrary patterns of inputs to be applied to the adder design. At each adder output, the multiplexer selects whether to include or not to include the adder in the measured results,. A switch on the FPGA board was wired to the select pin of the multiplexers. This allows measurements to be made to deduct out the delay due to the memory, the multiplexers, and interconnect (both external cabling and internal routing) [6].

IV. IMPLEMENTATION

Xing and Yu [7] noted that delay models and cost analysis for designs developed for VLSI technology does match the second, the parallel prefix network was analyzed to directly to FPGA designs. They compared the design of determine if a specific pattern could be used to extract the worst case delay. Considering the structure of the Generate-Propagate (GP) blocks (i.e., the BC and GC cells), we were able to develop the following scheme.
If we arbitrarily assign the (g, p) ordered pairs the values (1,
0) = True and (0, 1) = False, then the table is self-contained
and forms an OR truth table. If both inputs to the GP block are
false, then the output will be false; conversely, the output is
true if both the inputs are true, then. Hence, an input pattern that alternates between generating the (g, p) pairs of (1, 0) and (0, 1) will force its GP pair block to alternate states.
Likewise, it is easily seen that the GP blocks being fed by its predecessors will also change their states. Therefore, this scheme will ensure that a worse case delay will be generated in the parallel prefix network since every block will be active. In order to ensure this scheme works, the parallel prefix adders were synthesized with the “Keep Hierarchy” design setting turned on (otherwise, the FPGA compiler attempts to reorganize the logic assigned to each LUT). With this option turned on, it ensures that each GP block is mapped to one LUT, preserving the basic parallel prefix structure, and ensuring that this test strategy is effective for determining the critical delay. The designs were also synthesized for speed rather than area optimization [8].
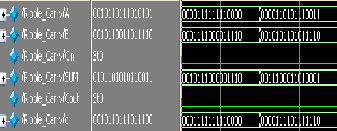
In the simulation process of kogge stone adder, a and b of
16 bits are taken as inputs and S and Cout are taken as output
Intermediate signals are G,C, l, m, q, r, s, t, v. In the
simulation process of sparse kogge stone adder, a and b of 16
bits are taken as inputs and S and C are taken as output Intermediate signals are considered as G, P, X. In the simulation process of spanning adder, a and b of 16 bits are taken as inputs and Sum and C are taken as output and the intermediate signals are g1,p1,x4,x8 and x12. In the simulation process of brent kung adder, a and b of 16 bits are taken as inputs and Sum and C. Finally adders like carryskip and ripple carry adders are compared with koggestone, sparse kogge, spanning tree and brent kung adders in terms of delay and power and are tabulated in the table1 given below.

V. SIMULATION AND SYNTHESIS REPORT

(a)

(b)
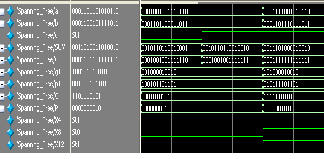
Fig.3: (a) Ripple carry adder simulated wave form (b)RCA
device utilization.

(a)

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 1505

ISSN 2229-5518

(b)
(b)
Fig.4: (a) Carry Skip adder simulated wave form (b) Carry skip device utilization.

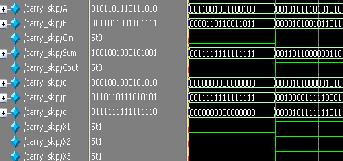
(a)
Fig.6: (a) Sparse kogge stone simulated wave form (b) SKS
device utilization.

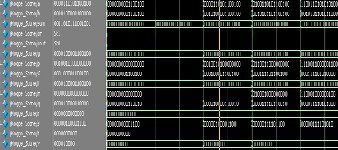
(a)
(b)
Fig.5: (a) Kogge stone simulated wave form (b) KS device utilization.

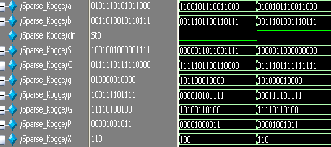
(a)
(b)
Fig.7: (a) Spanning tree simulated wave form (b) Spanning tree device utilization.


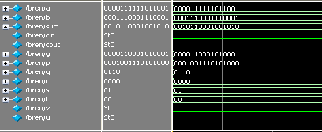
(a)

IJSER © 2013 http://www.ijser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 10, October-2013 1506

ISSN 2229-5518

(b)
Fig.8: (a) Brent kung simulated wave form (b) Brent kung device utilization.

VI DELAY AND POWER ANALYSIS

The synthesis of the above mentioned adders is done in Xilinx9.2i. The delay & power parameters are being observed and they are being compared between adders and parallel adders and then tabulated.
Table.1: Comparison of adders in terms of delay and power

VII CONCLUSION

From the results, it is concluded that the Brent kung adder provides better performance than Ripple Carry adder and Carry Skip adder. The power-delay performance can be increased with Sparse koggestone adder and Spanning tree adder. This is important where large number of adders to be used in precision arithmetic and cryptographic applications where the addition of numbers on the order of a thousand bits is very common. Because the adder is often the critical element which determines to a large part the cycle time and power dissipation for many digital signal processing and cryptographical implementations, For future FPGA designs it would be worthwhile to include an optimized carry path to enable tree-based adder. So these parallel prefix adders are the best choice in many VLSI application where power is the main constraint

ACKNOWLEDGMENT

It is very glad to take this opportunity to thank the Professor and Head of Department., Dr. M. Kamaraju, Gudlavalleru Engineering College for taking keen interest and for providing encouragement in my project work and I wish to express my deep gratitude and sincere thanks to my mentor guide Mr. Y. Sri Chakrapani for taking interest and for providing his co-
operation and guidance, which has helped me immensely, in completing this research work. I would like to thank the teaching and non-teaching Staff of Gudlavalleru engineering college for encouraging us for this research work.

REFERENCES

[1] K. Vitoroulis and A. J. Al-Khalili, “Performance of Parallel Prefix Adders Implemented with FPGA technology,” IEEE Northeast Workshop on Circuits and Systems, pp. 498-501, Aug. 2007.
[2] P. M. Kogge and H. S. Stone, “A Parallel Algorithm for
the Efficient Solution of a General Class of Recurrence
Equations,” IEEE Trans. on Computers, Vol. C-22, No 8,
August 1973.
[3] R. P. Brent and H. T. Kung, “A regular layout for
parallel adders,” IEEE Trans. Comput., vol. C-31, pp.
260-264, 1982.
[4] N. H. E. Weste and D. Harris, CMOS VLSI Design, 4th
edition, Pearson–Addison-Wesley, 2011.
[5] T. Lynch and E. E. Swartzlander, “A Spanning Tree Carry Lookahead Adder,” IEEE Trans. on Computers, vol. 41, no. 8, pp. 931-939, Aug. 1992
[6] P. Ndai, S. Lu, D. Somesekhar, and K. Roy, “Fine- Grained Redundancy in Adders,” Int. Symp. on Quality
Electronic Design, pp. 317-321, March 2007.
[7] S. Xing and W. W. H. Yu, “FPGA Adders: Performance
Evaluation and Optimal Design,” IEEE Design & Test
of Computers, vol. 15, no. 1, pp. 24-29, Jan. 1998.
[8] D. Harris, “A Taxonomy of Parallel Prefix Networks,”
in Proc. 37th Asilomar Conf. Signals Systems and
Computers, pp. 2213–7, 2003.
.

IJSER © 2013 http://www.ijser.org