The research paper published by IJSER journal is about Comparative Performance Analysis of MPSK and MQAM-Modulation Parameters on Orthogonal Frequency Division Multiplexing (OFDM) System over Flat and Frequency Selective Rayleigh Fading Channels with Doppler Frequency 1

ISSN 2229-5518

Comparative Performance Analysis of MPSK and MQAM-Modulation Parameters on Orthogonal Frequency Division Multiplexing (OFDM) System over Flat and Frequency Selective Rayleigh Fading Channels with Doppler Frequency

Md. Tanvir Hasan

Abstract— OFDM is a multicarrier modulation technology which has efficient spectrum utilization to support the transmission of high data rates. The typical subcarrier modulation schemes used in orthogonal frequency division multiplexing (OFDM) system includes: b inary phase shift keying (BPSK), phase shift keying (PSK) and quadrature amplitude modulation (QAM). This paper analyses the comparative performance of MPSK and MQAM on OFDM system that uses a range of number of PSK and QAM constellation points. Simulation is performed for various numbers of PSK and QAM (8 to 64-points) and with various Doppler frequency values (5 to 500 Hz) over flat and frequency selective fading channels. It is observed that the finest performance of OFDM system is with the number of QAM of 8 and maximum Doppler shift (MDS) of 5 Hz at all channels.

Index Terms— Minimum 7 keywords are mandatory, Keywords should closely reflect the topic and should optimally characterize the paper. Use about four key words or phrases in alphabetical order, separated by c ommas.

——————————  ——————————

1 INTRODUCTION

Orthogonal frequency division multiplexing (OFDM) divides the data into a large number of closely spaced sub- carriers, which are carefully selected so that each sub-carrier is orthogonal to the other sub-carriers. In the parallel OFDM transmission, each sub-carrier experiences flat fading rather than frequency-selective fading and the inter-symbol interference (ISI) can be reduced significantly. Since OFDM can provide high data rates over extremely hostile channels at a comparable low complexity, it has been chosen by many communication systems, including the European radio DAB and TV DVB-T [European Standard (DAB), 2001; European Standard (DVB), 2001], wireless local area networks (WLAN) (Part 11, 1999; BRAN, 2001), Wi-MAX, etc. OFDM is sensitive to Doppler and carrier frequency errors, which destroy the subcarrier orthogonality and results in inter-channel interference (ICI) (Song and Lim, 2003). This happens when a specific OFDM block duration is much smaller than the channel coherence time, i.e., relatively mild Doppler, the channel can be assumed to be approximately constant over the OFDM block (Song and Lim, 2003). QAM modulation scheme has been very popular in OFDM system since it offers wider range of envelope fluctuation as explains in [9]. Besides, it provides higher spectral efficiency due to the usage of

————————————————

Md. Tanvir Hasan

Master of Engineering in Telecommunications

Bachelor of Science in Electrical and Electronic Engineering

American International University-Bangladesh (AIUB)

E-mail : wirelesstanvir@gmail.com
amplitude and phase modulation which effectively increased the channel capacity [7].
Many research attempts have been performed to produce a better performance of OFDM system. The work in [11] discusses the performance of OFDM system with the asymmetric hexagonal 16-QAM modulation scheme over AWGN channel. The performance is compared with the conventional rectangular 16-QAM. In [2], describe in details, the effect of Doppler frequency using different pilot arrangements in wireless OFDM system, under Rayleigh fading channel conditions. The work in [3] considers the performance degradation of a high QAM modulated OFDM system over frequency selective time-varying fading channels. The degradation in the performance of OFDM system resulting from Doppler effects over time-varying, frequency selective Rayleigh fading channel is obtained by averaging the approximated ICI statistics over the ensemble fading. The work in [8] derives the exact BER expression for rectangular quadrature amplitude modulation (R-QAM) scheme. The OFDM system is corrupted by both asynchronous (CCI) and Nakagami-m fading. [1] Presents an evaluation for the effect of various modulation scheme combinations, i.e., target BER, Doppler frequency, and several adaptation intervals. The adaptation interval serves as the control period to improve the performance of adaptive OFDM. The works in [3] introduce a method of time-variant Doppler frequency estimation and compensation for mobile OFDM systems. The BER performances were based on 16-QAM and 64-QAM points

http://www.ijser.org

ISSN 2229-5518

over one-path fading channel and IMT2000 vehicular model B
channel.
The works concerning FFT-OFDM systems using QAM scheme, where the performances are evaluated under various channel conditions are readily available in [8, 10, 11]. However, to my best knowledge, no paper has been published on the performance analysis of the effect of various PSK and QAM-modulation points over FFT-OFDM system tested over flat and frequency selective Rayleigh fading channels with Doppler frequency.
The present contribution investigates the impact of the number of PSK and QAM constellation points over FFT- OFDM system tested over various channels. The performance analysis includes the FFT-OFDM system with Doppler frequency over flat fading and the frequency selective Rayleigh fading channels. Superiority of QAM of 8 than all other QAM points and also all PSK points and maximum Doppler shift (MDS) of 5 Hz at all channels is tested via simulation results. The rest of the paper is organized as follows: Section 2 illustrates an overview on small scale fading. Section 3 gives an impression on Doppler shift. Section
4 illustrates Rayleigh fading channel. An outline of basic
OFDM system model has provided in section 5. Simulation
results and analysis is given in section 6, and section 7
concludes this paper.

3 SMALL SCALE FADING

Small scale fading or simply fading is used to describe the rapid fluctuations of the amplitudes, phases, or multipath delays of a radio signal over a short period of time or travel distance so that large scale path loss effects may be ignored. Fading is caused by interference between two or more versions of the transmitted signal which arrive at the receiver at slightly different time. These waves are called the multipath waves, and are combined at the receiver’s antenna to produce a resultant signal which can vary widely in amplitude and phase, depending on the distribution of the intensity and relative propagation time of the waves and the bandwidth of the transmitted signal. Multipath in the radio channel creates small-scale fading effects. The three most important effects are [5] rapid changes in signal strength over a small travel distance or time interval, random frequency modulation due to varying Doppler shifts on different multipath signals and time dispersion (echoes) caused by multipath propagation delays. Many physical factors in the radio propagation channel influence small-scale fading. These include multipath propagation, speed of the mobile, speed of surrounding objects and the transmission bandwidth of the signal.

3 DOPPLER SHIFT

When a signal source and a receiver are moving relative to one another, the frequency of the received signal will not be
the same as the source. Consider a mobile moving at a constant velocity v, along a path segment having length d between points X and Y, while it receives signals from a remote source S, as illustrated in figure 1. The difference in path lengths travelled by the wave from source S to the mobile at points X and Y is Δl = d cos θ = vΔt cos θ where Δt is the time required for the mobile to travel from X to Y, and θ is assumed to be the same at point X and Y since the source is assumed to be very far way. The phase change in the received signal due to difference in path lengths is therefore [5]:

△

Hence, the apparent change in frequency, or Doppler shift, is
given by [5],

fd =

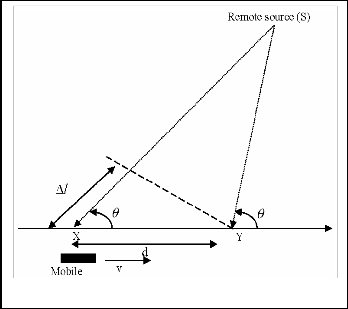
It can be seen from (2) that if the mobile is moving towards the direction of the wave arrival, the Doppler shift is positive. If the mobile is moving away from the direction of the wave arrival, the Doppler shift is negative [5].

Fig. 1. Illustration of Doppler Effect

In order to compare different channels and to develop some general design guidelines for wireless systems, parameters which closely quantify the multipath channel are used. These parameters include delay spread, and Doppler spread [5].

3.1 Delay Spread and Coherence Bandwidth

Delay spread and coherence bandwidths are parameters that describe the time dispersive nature of the channel in a local area. The time dispersive properties of wide band multipath channels are most commonly quantified by their mean excess delay (τ) and r.m.s delay spread (σ, τ). The mean excess delay is given by [5]:

http://www.ijser.org

ISSN 2229-5518

Where, P(τ) is the absolute power level of the received signal, and a2 = P(τ). The r.m.s delay spread is defined to be;

τ = (4)

Based on the multipath time delay spread, small scale fading can be classified into flat fading and frequency selective fading. In flat fading channel, bandwidth of the signal is smaller than the bandwidth of the channel. Also delay spread of the channel is smaller than the symbol period. In frequency selective fading, bandwidth of the signal is greater than the bandwidth of the channel. Similarly, delay spread of the channel is greater than the symbol period.

Where,

= (5)

On the basis of Doppler Spread, small scale fading can be further classified into fast fading and slow fading. Fast fading channel constitutes high Doppler spread, smaller coherence time than symbol period and also faster channel variations than baseband signal variations. Oppositely, slow fading channel is composed of low Doppler spread, higher coherence
These delays are measured relative to the first detectable
signal arriving at the receiver at τ0 = 0.

The coherence bandwidth, BC, can be defined as the relation derived from the r.m.s. delay spread. If the coherence bandwidth is defined as the bandwidth over which the frequency correlation function is above 0.9, then the coherence bandwidth is approximated as [5]:

≈

If the definition is relaxed so that the frequency correlation function is above 0.5, then the coherence bandwidth is approximated as [5]:

≈ (7)

3.2 Doppler Spread and Coherence Time

Doppler spread and coherence time are parameters which describe the time varying nature of the channel in small-scale region. Doppler spread, BD, is a measure of the spectral broadening caused by the time rate of change of mobile radio channel. It can be defined as the range of frequencies over which the received Doppler spectrum is essentially non-zero. Coherence time, Tc, is the time domain dual of Doppler spread which can be used to characterize the time varying nature of the frequency dispersiveness of the channel in the time domain. The Doppler spread and coherence time are inversely proportional to one another. That is,

From the above, it can be seen that the time dispersion and frequency dispersion mechanisms in a mobile radio channel lead to four-possible distinct effects. They are manifested depending upon the nature of the transmitted signal, the channel, and the velocity. The two-propagation mechanisms are independent of one another. Figure 2 shows a tree of the four different types of small-scale fading channels [5].
time than symbol period and slower channel variations than baseband signal variations. However, this paper only deals with flat and frequency selective channels in favor of less congestion.

4 RAYLEIGH FADING

The Rayleigh distribution is by far the most used one to model the fading phenomenon due to its simplicity, straight forward derivation from geometrical assumptions and fairly good agreement with experimental data. This is the case with no dominant line-of-sight link between transmitter and receiver, and the received real and imaginary parts of the fields are independent zero-mean Gaussian random variables. The PDF is given by:

FP (p) = (9)

Where, Pf again is the mean fast fading power, here equal to the mean power received. The received power under Rayleigh fading follows the above ―exponential" PDF. The standard deviation of the received power in this case can be found to be Pf as well. The simple form of the exponential pdf results in a simple cdf:

FP (p) = 1 – (10)

In many problems, our interest lies in the probability that the received power will fall below a specified level. Recalling that the CDF represents P [Prec < p], the CDF is precisely the function to be used for such questions, with p the specified minimum power level in Watts. In the case of Rayleigh fading, if we have values of p that are small compared to the mean received power Pf , the CDF can be simplified through a power series expansion of the exponential to:

FP (p) = 1 – (1 – ) = (11)

http://www.ijser.org

ISSN 2229-5518

The power level that will exceeded q percent of the time is then,

6 SIMULATION RESULTS

(1 - ) Pf (12)

5 OFDM SYSTEM MODEL

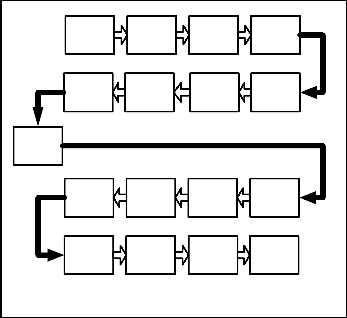
The OFDM system model is shown in figure 2. The input binary data streams are first passed through source encoder. Then, they are converted from serial to parallel data. These parallel data are then individually modulated by different carrier frequencies that are orthogonal to each other. In the present contribution, the modulation format is either MPSK or MQAM. The modulated data are then passed through IFFT block with N-points to convert them from frequency domain to time domain. IFFT data are used for generation of the OFDM symbols. A CP code is added to each IFFT output data which are then converted from parallel to serial. The resultant data are sent to the receiver over the channel after being converted to frame structure (serial data stream). The frame structure consists of the modulated data and a pilot signal that is used for channel estimation and compensation at the receiver. The channel consists of multipath fading (flat fading channel or frequency selective fading channel) with Rayleigh distribution. At the receiver, the inverse operations are employed. A serial to parallel conversion is done and the CP is removed for the signal. A FFT with N-points is used to convert the signal from time to frequency domain. The particular demodulation is performed and then the resultant demodulated data are converted from parallel to serial format which is further passed through source decoder to retrieve the original binary stream.
In this section, the comparative performance of MPSK and
MQAM is investigated via simulation. Four QAM points (8,

16, 32, and 64) and four PSK points (8, 16, 32, and 64) are used to detect the better modulation scheme. The simulation parameters are illustrated below:

TABLE 1

SIMULATION PARAMETERS

Parameter Value

Number of subcarriers 512

Number of sub-band 32

Number of subcarriers per 16

sub-band

TABLE 1

SIMULATION PARAMETERS

Parameter Value

IFFT Size 512
Modulation Scheme MPSK (8, 16, 32, 64),
MQAM (8, 16, 32, 64)
Carrier frequency 2GHz
Guard Time Duration 128
SNR 5dB, 15 dB, 25dB and 35
dB
Bit rate 5 Mbps

Binary Data Stream

Source

Encoder

Serial to Paraller Converter

Modulator

Sampling frequency 5.4 MHz
Frame size 6
Bandwidth 5 MHz

Rayleigh

Fading

Transmitter

FFT

Demodulator

Parallel to Serial Converter

Cyclic Prefix Removal

Parallel to Serial Converter

Cyclic Prefix Extension

Serial to Paraller Converter

Source

Decoder

IFFT

Receiver

Binary Data Stream

6.1 Performance in Flat Fading Channel

In this section, the used channel model is the flat fading, where the bandwidth of the transmitted signal is smaller than the coherence bandwidth of the channel. Then, all frequency components of the transmitted signal undergo the same attenuation and phase shift in transmission through the channel. Three-values of the Doppler frequency are used in this simulation; these are 5 Hz, 50 Hz and 500 Hz.
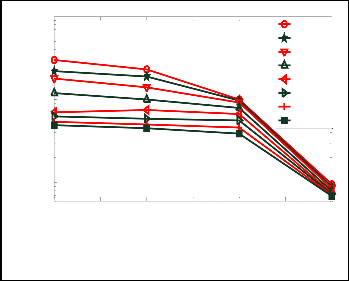
The BER performance of FFT-OFDM system with PSK and QAM of 8, 16, 32 and 64 for Doppler frequency of 5 Hz, 50 Hz and 500 Hz are depicted in figure 3, figure 4 and figure 5 respectively. For each QAM parameter, the system is

Fig. 2. OFDM system model

simulated using these three different maximum Doppler shift
(MDS) values.

http://www.ijser.org

ISSN 2229-5518

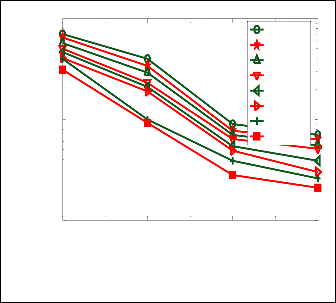
It shows that FFT-OFDM performs well at the lower Doppler frequency as compared to its performance at the higher frequency. The performance is reduced as the number of
constellation mapping points increased from 8 to 16, 32, 64 0
point. 10
These results also reveals that FFT-OFDM performs better with QAM constellation mapping of 8-points as compared all other constellations points including 16QAM, 32 QAM,
64QAM, 8PSK, 16PSK, 32PSK and 64PSK. At all cases BER

-1

performance of MQAM is slightly improved than MPSK. 10

64PSK

64QAM

32PSK

32QAM

16PSK

16QAM

8PSK

8QAM

-2

5 10 15 20 25 30 35

SNR(dB)

Fig. 5. Comparative BER performance of FFT-OFDM for MPSK

and MQAM (8, 16, 32 and 64 points) in flat fading channel, at MDS

= 500 Hz. ng

-1

10 64PSK

64QAM

32PSK

32QAM

16PSK

-2 16QAM

10 8PSK

8QAM

-3

5 10 15 20 25 30 35

SNR(dB)

Fig. 3. Comparative BER performance of FFT-OFDM for MPSK

and MQAM (8, 16, 32 and 64 points) in flat fading channel, at MDS

= 5 Hz.

10 64PSK

64QAM

32PSK

32QAM

-1 16PSK

10 16QAM

8PSK

8QAM

Channel

The BER performance of the FFT-OFDM systems in the frequency selective fading channel is presented in this section. This channel indicates that the transmitted signal has a bandwidth greater than the coherence bandwidth of the channel. The frequency components of the transmitted signal with frequency separation exceeding the coherence bandwidth are subjected to different gains and phase shifts. The path gain
8 dB and the path delay is 1 sample.
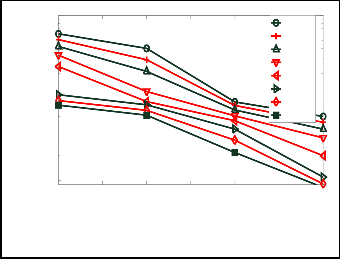
The BER performance of FFT-OFDM system with PSK and QAM of 8, 16, 32 and 64 for Doppler frequency of 5 Hz, 50 Hz and 500 Hz are depicted in figure 6, figure 7 and figure 8 respectively. For each QAM parameter, the system is simulated using these three different maximum Doppler shift (MDS) values (5 Hz, 50 Hz and 500 Hz). It can be seen that the BER is minimum for lower Doppler frequency (5 Hz). The error increases as the number of constellation points increases for a range of SNR values.
These simulation results also reveal the same approach in flat fading scenario. These results again illustrate that FFT-OFDM performs better with QAM constellation mapping of 8-points as compared to all other constellations points including
16QAM, 32 QAM, 64QAM, 8PSK, 16PSK, 32PSK and 64PSK. Again at all cases BER performance of MQAM is slightly improved than MPSK.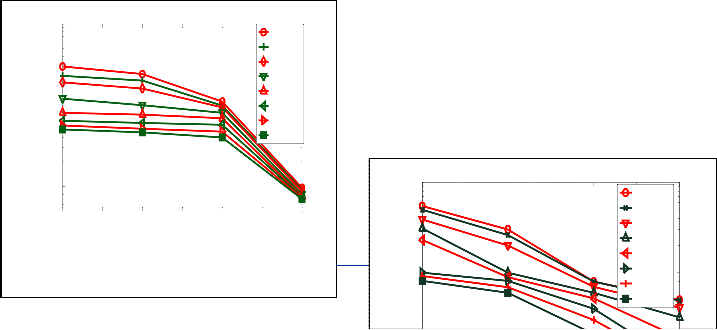

-2

5 10 15 20 25 30 35

SNR(dB)

Fig. 4. Comparative BER performance of FFT-OFDM for MPSK

and MQAM (8, 16, 32 and 64 points) in flat fading channel, at MDS

= 50 Hz.

-1

JSER ©

://www.ij -2

64PSK

64QAM

32PSK

32QAM

16PSK

16QAM

8PSK

8QAM

ISSN 2229-5518

number of constellation mapping points increased from 8 to
64-point. The FFT-OFDM system in frequency selective fading
channel has low BER performance for lower Doppler
frequency and the error increases as the number of
constellation points increased for a range of SNR values.

REFERENCES

[1] Ahn’, C.J. and Sasase, L. (2002) ‘The effects of modulation combination, target BER, Doppler frequency, and adaptation interval on the performance of adaptive OFDM in broadband mobile channel’, IEEE Transactions on Consumer Electronics, Vol.

48, No. 1, pp.167–174.

[2] Arshad, K. and Sheikh, A.U.H. (2004) ‘Effect of Doppler frequency on pilot arrangements in wireless OFDM systems’, Proc. IEEE International Conference on Information and Communication Technologies: From Theory to Applications, Nos. 19–

23, pp.261–263.

[3] Cai, J., Li, Z., Hao, Y. and Cai, J. (2006) ‘Time-variant Doppler frequency estimation and compensation for mobile OFDM systems’, IEEE Transactions on Consumer Electronics, Vol. 52, No.

2, pp.336–340.

10 64PSK

64QAM

32PSK

32QAM

16PSK

10-1 16QAM

8PSK

8QAM

-2

5 10 15 20 25 30 35

SNR(dB)

Fig. 7. Comparative BER performance of FFT-OFDM for MPSK and MQAM (8, 16, 32 and 64 points) in frequency selective fading channel, at MDS = 50 Hz.

7 CONCLUSION

This paper has noticeably revealed that MQAM performs more efficiently than MPSK in both flat and frequency selective Rayleigh fading channel with Doppler frequency in term of bit error rate. The present contribution also demonstrates that the performance of the FFT-OFDM system is affected by Doppler frequency as well as the value of PSK and QAM constellation points. The FFT-OFDM system simulated in flat fading channel performs better at the lower Doppler frequency as compared to its performance at the higher Doppler frequency. The performance is reduced as the

[4] Chen, S. and Yao, T. (2004) ‘Inter-carrier interference suppression and channel estimation for OFDM systems in time- varying frequency-selective fading channels’, IEEE Transactions on Consumer Electronics, Vol. 50, No. 2, pp.429–434.

[5] Hadi, W.A.H. (2006) ‘Enhancement of DWT-OFDM-CDMA system using turbo coding’, PhD thesis, University of Technology, Baghdad/Iraq.

[6] Hara, Sh. and Prasad, R. (2003) Multicarrier Techniques for 4G Mobile Communications, Artech House, Boston London.

[7] Jain, P. (2002) ‘On the impact of channel and channel quality estimation on adaptive modulation’, MSc thesis, Faculty of the Virginia Polytechnic Institute and State University, USA.

[8] Liu, X. and Hanzo, L. (2006) ‘Exact BER of rectangular- constellation QAM subjected to asynchronous co-channel interference and Nakagami-m fading’, Electronics Letters, Vol.

42, No. 15, pp.868–869.

[9] Song, W.G. and Lim, J.T. (2003) ‘Pilot-symbol aided channel estimation for OFDM with fast fading channels’, IEEE Transactions on Broadcasting, Vol. 49, No. 4, pp.398–402. Stüber, G.L. (2002) Principles of Mobile Communication, 2nd ed., Georgia Institute of Technology, Atlanta, Georgia.

[10] Wang, T., Proakis, J.G. and Zeidler, J.R. (2003) ‘Performance analysis of high QAM OFDM system over frequency selective time-varying fading channel’, Proc. 14th IEEE International Symposium on Persona1, lndoor and Mobile Radio Communication Proceedings, pp.793–798.

[11] Xingxin, G., Mingquan, L. and Zhenming, F. (2002)

‘Asymmetric hexagonal QAM based OFDM system’, Proc. IEEE International Conference on Circuits and Systems and West Sino Expositions, 29 June–1 July, Vol. 1, pp.299–302.

http://www.ijser.org

International Journal of Scientific & Engineering Research Volume 3, Issue 5, May-2012 7

ISSN 2229-5518

h tt p ://www .llser. ora