𝑀𝑃𝐹𝑖𝑙 =
International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 950
ISSN 2229-5518
Comparative Analysis of Transmission Fixed Cost Allocation Methods: Postage Stamp, Marginal Participation Factors and Power Tracing
Heramb Mayadeo, Dr. (Mrs) A. A. Dharme
—————————— ——————————
N a competitive power market environment, proper transmission pricing scheme, as per FERC guidelines mentioned in order 888 & 889 could meet revenue expectations, promote an efficient operation of electricity markets, encourage investment in optimal locations of generation and transmission lines, and adequately reimburse owners of transmission assets. Most important, the pricing scheme should implement fairness and be
practical [1].
However, it is difficult to achieve an efficient transmission pricing scheme that could fit all market structures in different locations [2].The major part of the cost of the transmission system is fixed cost or sunk cost unlike the generation business. This makes the transmission pricing an even more challenging problem in addition to the challenges posed by the nature of electricity. The amount of research on this issue indicates that there cannot be a single transmission pricing scheme which will satisfy all the criteria discussed so far. Hence gamut of methods are developed on the basis of the characteristics of particular network for which transmission pricing scheme is being designed [3].
The most common and unsophisticated approach which was being used widely in the earlier days of deregulation is postage stamp method. In this method there is no attention paid to the actual system usage and the cost allocation is done on the basis of average system costs.
————————————————
• Heramb Mayadeo is currently pursuing Master’s degree program in Electrical Engineering in College of Engineering, Pune – 5, India, (+91) 98601-47193, mheramb@gmail.com
The user simply pays the charge at a rate equal to a fixed
charge per unit of energy transmitted within a particular utility system. What makes this pricing scheme obsolete In addition to this is its inability to accommodate congestion constraints. To introduce fairer and more transparent charges; methods needed to be technically sound and must be able to calculate rates as per actual usage of the system. This encouraged researchers to go for more complex but technically sound methods. One of the very elaborate methods is marginal participation method [4], [5]. This method is based on sensitivity factors of transmission lines and provides locational price signals as well as it can be used to allocate congestion charges.
Another power flow based method is power tracing or average participation method. This was proposed in 1996 almost simultaneously and completely independently by Bialek [6] and Kirschen [7]. Both the approaches are based on proportional sharing principle [8], [9]. Both of these methods determine the contribution of transmission users towards transmission usage. But, both of these methods differ in their approach towards solving the problem. Bialek’s method is based on simultaneous equations approach whereas Kirschen’s method employs graph theory. Another approach based on graph theory is proposed by Felix Wu [10] which is considered in forthcoming analysis.
• Dr. (Mrs.) A. A. Dharme is Associate Professor in Electrical
Engineering Department, College of Engineering, Pune – 5,
IJSER © 2013
International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 951
ISSN 2229-5518
This is a traditionally used method by electricity companies to allocate fixed transmission charges among the users of firm transmission service. This is an
embedded cost method or rolled-in cost method. This is the simplest and probably the crudest method as it does not require any power flow calculations and it does not account for the transmission distance and network configuration. The basic assumption of this method is, entire transmission system is used, regardless of the actual facilities that carry the transmission service. The charges are allocated on the basis of average embedded cost and the magnitude of user’s transacted power as per
In this case only positive changes in power flow of a corridor are considered, as this is how it has been implemented traditionally wherever it is used. But, a
version can be developed where negative changes in power flow are considered and are paid instead of being charged. This being a marginal method it is necessary to weight each usage factor by amount of load the unit of Uil becomes MW2h.
The marginal participation factor of ith load/generator over lth corridor is given by equation (3).
𝑈𝑖𝑙
equation (1).![]()
𝑀𝑃𝐹𝑖𝑙 =
𝑖 𝑖𝑙
(3)
𝑃𝐿𝑖
![]()
𝐶𝑖 = 𝑇𝑇𝐶 𝑛
𝑖=1
Where,
𝑃𝐿𝑖
(1)
This method is dependent on the selection of slack bus to
run the power flow. The values of participation factors change once the slack bus is changed. This is applied in Chilean and Argentinean systems where a slack bus is
Ci - Charge allocated to ith node, TTC – Total transmission cost, PLi - load in MW at ith bus, n -number of nodes
Apart from its only merit i.e. simplicity this method suffers numerous demerits. This method does not account for the actual system usage and/or congestion in the system. No locational pricing signals are provided by this method. Also, the user at the farthest end of the system is always at benefit since it uses the system most and pays only for the proportion of the load connected at its bus.
This is a power flow based method and makes use of sensitivity factors and makes use of extent of use criterion to allocate charges among the system users. This method is also called as “areas of influence” method in Chile and Argentina. The usage is defined as incremental i.e. the incremental change in power flow in each corridor (line) is computed for 1 MW incremental increase in load/generator at each load node. Once the power flow variation in each corridor is obtained for incremental increase in each load/generator the usage index is calculated as per equation (2).
defined and the systems are radial with a strong load in centre and secondly line capacity limits are ignored. Otherwise more advanced technique can be used as given by [11].
Both the approaches of power tracing viz. simultaneous equations [6] [12] & graph theoretic [7] [10] are based on the proportional sharing principle. It states that “the nodal inflows are shared proportionally among nodal outflows [8]”. Graphically it is illustrated in Fig. 1
𝑈𝑖𝑙 = ∑ 𝑖 (�𝐹𝑖 � − |𝐹 |)𝑃
𝑙
(2)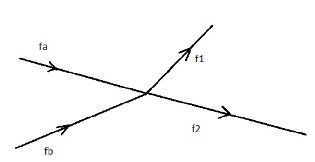
Fig.1 Proportional sharing principle
Where, Fl is the base case power flow of the corridor, Fli is
the power flow in corridor l when load/generator at ith![]()
𝑓 = 𝑓 𝑓𝑎
𝑓 +𝑓
![]()
+ 𝑓 𝑓𝑏
𝑓 +𝑓
(4)
𝑎 𝑏
𝑎 𝑏
bus is increased by 1 MW, Pi is the power
𝑓2 = 𝑓2 𝑎 + 𝑓 𝑏
(5)
𝑓 𝑓
2 𝑓 +𝑓
consumed/generated by ith load/generator resp., Uil is the
𝑓𝑎 +𝑓𝑏
𝑎 𝑏
usage factor of ith load over lth corridor.
The assumptions made are,
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 952
ISSN 2229-5518
• Kirchhoff’s current law must be satisfied for all the nodes in the network
• Network node is a perfect mixer
Power tracing algorithms provide us with,
• Contribution of generators in line flows
• Contribution of loads in line flows
• Load generation interaction
• Loss allocation
The simultaneous equations approach is easy to code but requires distribution matrix inversion and which is very difficult for a large system as distribution matrix can be singular due to its sparse nature. On the other hand graph theoretic approach does not involve matrix inversion and it is very intuitive but it is difficult to code. In the forthcoming discussion graph theoretic approach is used, in particular Wu’s method is implemented. Following assumptions are made to simplify the problem,
• An AC load flow solution is available from on- line state estimation or off-line system analysis
• No loop flows are present
• The line active and reactive power flows keep constant along the line, each edge has a definite direction and the network is lossless.
• A generator has the priority to provide power to the load on the same bus
• The flows of electricity obey the proportional sharing rule
Bus-line incident matrix (BLIM) can be used to form bus- inflow-line (BILIM) and bus-out flow line (BOLIM) incident matrices respectively and determine the pure sink and pure source of the system. A pure source node is that node on which no power inflows exist. A pure sink node is one in which no power outflows exist. This
on these lines to the receiving end nodes as generation contribution of generator on pure source node. Load on this bus is considered as an additional outflow.
• Once the pure source and corresponding lines
have been deleted, search for a new pure source. Delete this node and also remove the lines connected to this node. Carry forward the flows on these lines to the receiving end node as generation contribution of generator on pure source node. This is done on proportional sharing basis. Load is considered as an additional outflow on that node
• Repeat this process till all pure sources are exhausted. That means, the nodes which are left are the pure sinks. A pure sink is a node on which only inflows exist. A system can have multiple pure sinks
This downstream tracing (DSTR) algorithm is applied to obtain the contribution factors of individual generators to line flows and loads. The state variable in DSTR is the net generator power. Following matrices are calculated
• Extraction factor matrix of lines and loads from bus total passing power
• The other is contribution factor matrix of generators to bus total passing power
The product of these two matrices constitutes the contribution factors of generators to line flows and loads.
Extraction factors of lines from bus total passing power,
𝑃𝑙 = 𝐴𝑙 𝑃 (6)
where, Pl is the vector of line power, P is the vector of bus
passing power in the bus sequence of downstream tracing
algorithm & extraction factor matrix of lines Al is calculated as follows
𝑙𝑖𝑛𝑒 𝑗 ′𝑠𝑝𝑜𝑤𝑒𝑟 𝑓𝑙𝑜𝑤
method is also proposed in two versions: upstream
looking algorithm and downstream looking algorithm. In
this paper downstream looking algorithm is considered.
Both the algorithms are dual of each other and give same![]()
(𝐴 ) =
𝑏𝑢𝑠 𝑖 ′𝑠𝑡𝑜𝑡𝑎𝑙 𝑝𝑎𝑠𝑠𝑖𝑛𝑔 𝑝𝑜𝑤𝑒𝑟 𝑃𝑖
Similarly, extraction matrix of loads AL is calculated as
(7)
results. A very lucid explanation and procedure for downstream looking algorithm is given in [13], as
(𝐴𝐿 )𝑖𝑗 = 0 𝑖 ∈ 𝑛𝑒𝑡 𝑙𝑜𝑎𝑑 𝑏𝑢𝑠 (8)![]()
𝑛𝑒𝑡 𝑙𝑜𝑎𝑑 𝑜𝑛 𝑏𝑢𝑠 𝑖
follows,
=
𝑃𝑖
𝑖𝑛𝑒𝑡 𝑙𝑜𝑎𝑑 𝑏𝑢𝑠 (9)
• Start with a node which has highest. This node is
called as a pure source. A pure source is defined
as a node on which only real power outflows exist and there are no inflows of real power. Delete this node and also remove the lines connected to this node. Carry forward the flows
The extraction factor matrix of lines and loads (combined)
is obtained as follows
𝐴 = � 𝐴𝑙 � (10)
𝐴𝐿
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 953
ISSN 2229-5518

The matrix A has one and only one non-zero element in each row and the sum of elements in every column is one.
Contribution factors of generators to bus total passing power,
The contribution factor matrix B is defined as,
𝑃 = 𝐵𝑃𝐺 (11)
Where, PG is the vector of generator power. The matrix B
is formed row by row. The elements are calculated as
follows
𝐵𝑏𝑢𝑠−𝑖,𝑏𝑢𝑠−𝑘 = 1 (𝑘 = 𝑖, 𝑘 ∈ 𝑛𝑒𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑖𝑜𝑛 𝑏𝑢𝑠)
= 0 (𝑘 = 𝑖, 𝑘 ≠ 𝑛𝑒𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑖𝑜𝑛 𝑏𝑢𝑠)
= 0 (𝑘 > 𝑖) (12)
= 0 (𝑘 < 𝑖, 𝑘 ≠ 𝑛𝑒𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑖𝑜𝑛 𝑏𝑢𝑠)
= ∑𝑙𝑗∈𝑖(𝐴𝑙𝑗−𝑚 𝐵𝑚−𝑘 ) (𝑘 < 𝑖, 𝑘 ∈
𝑛𝑒𝑡 𝑔𝑒𝑛𝑒𝑟𝑎𝑡𝑖𝑜𝑛 𝑏𝑢𝑠)
Where,
k > i means k is downstream bus of i & hence all corresponding elements are 0 as they do not affect the passing power of the upstream bus.
k < i means k is an upstream bus of i. lj ϵ i means line j is inflow of bus i.
Alj−m is the unique nonzero element corresponding to line in matrix Al with bus m as its upstream terminal. Bm−k is the element in matrix already calculated which represents the contribution of generator to the total injection power of bus m. The product of above two terms represents the contribution of generator k to the total injection power of bus through line (from bus m to bus k).
The contribution factors of individual generators to line flows and loads are calculated as follows,
𝑃𝑙 = 𝐴𝑙 𝑃 = 𝐴𝑙 𝐵𝑃𝐺 = 𝐾𝑙𝐺 𝑃𝐺 (13)
𝑃𝐿 = 𝐴𝐿 𝑃 = 𝐴𝐿 𝐵𝑃𝐺 = 𝐾𝐿𝐺 𝑃𝐺 (14)
Throughout this paper the system taken as a reference is an IEEE 30 bus modified system. All the considered methods are implemented on this modified system presented in Fig. 2. The single line diagram of the system is as follows,
Fig 2 Modified IEEE 30 bus system
The system data is given in appendix D of [8]. The assumptions made are,
• The total sunk cost of the transmission network to be recovered is considered Rs. 10, 00,000/-
• Cost of each line is proportional to its reactance
(X)
• Half of the cost will be recovered from loads and half will be from generators
• System is considered as lossless (R is neglected
for using DC power flow)
• Only sunk (fixed) cost is considered
The nodal charges in Rs/MW obtained after
implementing the three discussed methods are as follows
TABLE 1
Nodal charges in Rs/Mw for loads
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 954
ISSN 2229-5518
TABLE 2
Nodal charges in Rs/Mw for loads
Volatility (%) | 104% | 57% | 0% |
Cost Recovery Factor (%) | 96% | 75% | 100% |

Figure 3. Comparison of nodal charges for loads
TABLE 3
Demand network use rate statistics
TABLE 4
Generation network use rate statistics
Figure 4. Comparison of nodal charges for generators
The system under consideration is characterized by concentration of generation at one end and loads spread throughout the length of the system, hence it is almost a radial system.
From table I and fig. 3 it is observed that the locational price signals are best provided by APF (Power tracing) method as it considers the system usage and nodal demand values, on the other hand MAPF method uses sensitivity of a load/generator for a particular line flow
IJSER © 2013 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 4, Issue 6, June-2013 955
ISSN 2229-5518
and hence the charges vary as per the sensitivity and not the actual usage of system and fail to provide good locational signals. PS method totally fails to provide any
kind of locational signals.
From table III, APF method has lesser rate volatility (defined as the ratio of σ and average) for loads as compared to MAPF method whereas table IV shows exactly opposite behaviour in case of generators. Similar contrast is observed in case of σ values in case of loads and generators. This indicates that APF method is a better indicator for network usage with lesser volatility in case of wide spread loads. In PS method no network usage is indicated since system usage is considered on averaged basis which also causes pancaking of charges.
The cost recovery factor (ratio of total cost recovered to total sunk cost) is 100% for postage stamp method but according to DC power flow results line numbers 16 (from bus 12 to bus 13) and 13 (from bus 9 to bus 11) have zero power flow hence zero usage. Hence whether to recover the cost of these unused lines from existing customers or not becomes the policy related issue. But, APF method, being usage based method has less than
100% cost recovery factor indicating that only the cost of actual usage of network has been recovered from existing users. From table III and IV it is evident that APF method is the best method as far as the actual usage based cost recovery is considered. MAPF method has a very poor cost recovery factor for generators.
Hence for a network having similar characteristics to that of considered system APF method is most suitable for fixed cost allocation since it reflects actual network usage, creates moderate price signals, moderate cost recovery and avoids pancaking.
The authors would like to thank Prof. Dr. Abhijit Abhyankar (Assistant Prof., IIT Delhi) for his invaluable guidance and support. Without his involvement the work would not have been completed.
[1] A. R. Abhyankar, “Issues in open access congestion, ATC, transmission pricing, loss allocation, UI pricing.” Training Seminar for MSETCL Officers, October 2012.
[2] D. Kirschen and G. Strbac, Fundamentals of Power
Systems Economics. No. pp. 49-72,141-204, Wiley, 0-470-
84572-4, 2001.
[3] J. W. M. Lima, “Allocation of transmission fixed charges: An overview,” 0885-8950/96, pp. 1409–1418, IEEE Transactions on Power systems, August 1996.
[4] F. J. Rubio-Od´eriz and I. J. P. Arriga, “Marginal pricing of transmission services: A comparative analysis of network cost allocation methods,” vol. 15, pp. 448–454, IEEE Transactions on Power Systems, February 2000.
[5] I. Perez-Arriaga, F. J. Rubio, J. F. Puerta, J. Arceluz, and J. Marin, “Marginal pricing of transmission services: an analysis of cost recovery,” Power Systems, IEEE Transactions on, vol. 10, no. 1, pp. 546–553, 1995
[6] J. W. Bialek, “Tracing the flow of electricity,” vol. 143, pp. 313–320, IEEE Proc.-Gener. Transm. Distrib., July
1996.
[7] R. Allen, D. Kirschen, and G. Strbac., “Contribution of individual generators to loads and flows,” vol. 12, pp. 52–
60, IEEE Transactions on Power systems, Feb 1997
[8] M. Shahidehpour, H. Yamin, and Z. Li, Market Operations in Electric Power Systems: Forecasting, Scheduling and Risk Management. No. pp 369-453, Wiley-Interscience,
0-471- 22412-X, 2002.
[9] Z. Jing and F. Wen, “Discussion on the proving of proportionality sharing principle in electricity tracing method,” pp. 1–5, IEEE/PES Transmission and Distribution Conference & Exhibition: Asia and Pacific Dalian, China, 2005.
[10] F. F. Wu, Y. Ni, and P. Wei, “Power transfer allocation for open access using graph theory: Fundamentals and applications in systems without loop flow,” vol. 15, pp. 923–929, IEEE Transactions on Power Systems, August 2000.
[11] H. Rudnick, R. Palma, and J. Fernandez, “Marginal pricing and supplement cost allocation in transmission open access,” Power Systems, IEEE Transactions on, vol. 10, no. 2, pp. 1125–1132, 1995
[12] J. Bialek, “Topological generation and load distribution factors for supplement charge allocation in transmission open access,” Power Systems, IEEE Transactions on, vol. 12, no. 3, pp. 1185–1193, 1997.
[13] A. R. Abhyankar, S. A. Khaparde, and C. V. Dobariya, “Tracing the flow of electricity - power flow tracing simplified (an explanatory note),”
IJSER © 2013 http://www.ijser.org