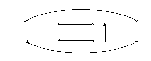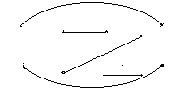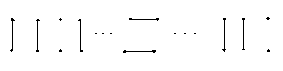International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 786

ISSN 2229-5518

CONSTRUCTION OF f-DIAGRAM

J.EvangelineJeba1,Dr.Jeyabharathi2

1Department of Mathematics, Lady Doak College, Madurai

2Department of Mathematics, Thiagarajar Engineering College, Madurai heart28_sweety@yahoo.co.in

Abstract:

In this work we study how to construct the f-diagrams and the product of two f-diagrams and also the definition of Brauer Algebra.

Keyword:

BrauerAlgebra, f-diagram

1. INTRODUCTION:

In the beginning of 20th century invariant theorists began to study the commuting algebras of the tensor powers of defining representations for the
classical groups G = Gl(n,C), Sl(n,C), O(n,C), So(n,C) and Sp(2m,C).
These algebras may be defined as follows. Let G be a classical group. Let V be its defining representation, and let TfV be the f th tensor power of
V. (i.e.,) TfV = V1 ⊗ V2 ⊗ ... ⊗Vf. . The group action
of G on V lifts to the diagonal action of G onTfV
defined by g.(V1 ⊗ V 2 ⊗ .... ⊗Vf) = (gV1 ) ⊗ (gV 2 ) ⊗
...⊗ (gVf). Define the commuting algebra EndG (TfV)
of this action to be the algebra of all linear
transformations of TfV which commute with this action of G. In the case of G = Gl (n, C) Schur showed that there is a surjective algebra homomorphism from CSf onto End Gl (n,C) (TfCn),
which is an isomorphism for f ≤ n. The kernel of this
homomorphism, gives a complete explanation of the
centralizer algebra
End Gl (n,C) (TfCn).
In 1937, when G = O(n,C) and Sp(2m,C) Richard Brauer defined two algebras Af (x)and Bf(x) where ‘f’ is a positive integer and ‘x’ is a real
indeterminate. The surjective algebra homomorphism for the algebras Af(x)and Bf (x) are constructed as follows:-

φf (n): Af (n) End o(n,R) (TfRn)

χf (2m): B f (2m) End sp(2m,R) (TfR2m)

If n and m are large enough then these homomorphisms are isomorphisms. When these homomorphisms are not an isomorphism then Richard Brauer failed to give the explanation of the kernel of the maps. In order to give a clear explanation of these kernels, Phil Hanlon and David Wales began to study the structure of the algebras A f(x) and Bf (x) where ‘x’ is an arbitrary real. The
algebras Af(x) and Bf(-x) are isomorphic to each other. So it was only necessary to study the algebra
A f(x).
The authors were able to describe the radicals of A f(x) and the matrix ring decomposition of A f (x) /Rad (Af (x)). Later this problem was reduced to the problem of computing the ranks of certain combinatorially defined matrices Zm ,k(x).

2.f-diagrams and brauer algebra

2.1. DEFINITION:

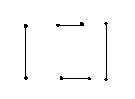
Let ‘f’ be a positive integer. An f-diagram‘d’
is a graph with 2f vertices and f edges such that each edge connects exactly two vertices and each vertex belongs to exactly one edge.

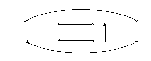
2.2. EXAMPLE:

is a 5-diagram.

3.Representation of an f- diagram:

An f- diagram, ‘d’ will be represented by a graph with 2f vertices in a plane arranged in two rows one upon the other, each of ‘f’ aligned vertices, the points 1,2,...,f in a top row denoted by t(d) and the points f+1, f+2,...,2f in a bottom row denoted by b(d) the vertices being labelled in the natural order from left to right.

3.1DEFINITION:

An edge connecting two vertices in the same
row (top or bottom) will be called a horizontal edge.
An edge connecting two vertices in different rows (one in the top row and other one in the bottom row) will be called a vertical edge.

3.2REMARK:

In any f-diagram the number of horizontal
edges in the top row is equal to the number of horizontal edges in the bottom row.

3.3DEFINITION:

An f-diagram‘d’ having no horizontal edges will correspond to a permutation σ in Sf and will be
called a permutation diagram or simply a permutation.In this case the ith vertex of the top row
will be connected to the σ (i)th vertex of the bottom
row.

3.4NOTATION:

Let C[x] be the ring of polynomials in the indeterminate x over the field C of complex numbers.
Let C(x) be the field of quotients of C[x]. Let Pf denote the set of all f-diagrams. Let Vf be the vector space over the field C(x) whose basis is the set Pf.

3.5DEFINITION:

Any f-diagram d in Pf will have 2f vertices and f edges. There are (2f-1) possibilities to join the first vertex with any other vertex, then 2f-3
possibilities for the next one and so on.
Thus the number of f-diagrams is (2f-1) (2f-
3)...5.3.1.
(i.e.,)│ Pf│ = (2f – 1) (2f – 3)....5.3.1.

3.6EXAMPLE:

The number of 4 diagrams is 105.

4.Multiplication of two elements in vf ;

We define the multiplication of any two
elements in Vf as follows: Let d1, d2 Є Pf
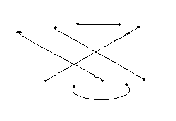
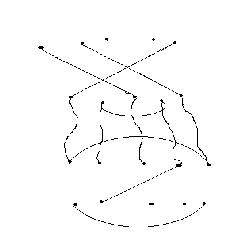
To obtain the product d1 d2 , we proceed as follows:

STEP 1:

Draw d2 below d1

STEP 2 :

Connect the ith vertex of the top row of d2 with the ith vertex of the bottom row of d1 by a vertical dotted line.

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 787

ISSN 2229-5518

Identify the path connecting the vertices in
the top row of d1 and vertices in the bottom row of d2
d2 .
diagram.
Also identify the cycles in the conjoined in

STEP 3:

Let m be the number of cycles in the
conjoined diagram obtained in step2.
If d is the diagram without cycles, then the product d1
.d2 of d1 and d2 is obtained by d1 . d2 = xm. d.
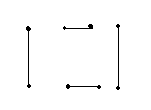
d1

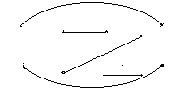
d2
d1 d2

d1 d2
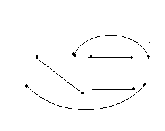
The resultant diagram is
X.

The resultant diagram is

REMARK:

The multiplication of two

4.1 EXAMPLE :-

d1
permutation diagram is compatiable with the multiplication of two permutations in Sf.

DEFINITION:

The multiplication defined above on the basis elements Pf of the vector space V f is extended linearly to arbitrary elements of Vf in accordance to the distributive law so as to make it into an algebra over C(x). This algebra is called Brauer algebra and will be denoted by Df (x).

Properties of Braueralgebra Df (x):

(i) Do =C(x) C D1(x) C D2 (x) C ...
(ii) Df(x)contains the group algebra CSf as a
subalgebra, Sfis the symmetric group on f symbols.
(iii) Df(x) is a unital algebra with as the unit element.

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013 788

ISSN 2229-5518

(iv) Df (x) is an associate algebra.

5.GENERATORS:

5.1DEFINITION:

Let ei be the f-diagram that connects the point i to i+l in the top row as well as in the bottom row and all other vertices in the top row are connected to the same vertices in the bottom row.
ei =
i i+1

Let gi be the diagram that connects the ith vertex of the top row with the (i+1)th vertex of the bottom row and (i+1)th vertex of the top row and to the ith vertex of the bottom row and to ith vertex of the bottom row and all other lines. connect the same points of the top
row with that of the bottom row. gi =
i i+1

5.2Properties of generators:-

gi2= 1, identify ei 2= x. ei
gig j = gjgi if lj-il>1 gig i+1 g i = gi+1 gig i+1 ei ei-1 ei =ei
ei-1 ei ei-1 =ei-1
ei g i= gi ei= ei
ei ei+1 ei =ei
ei+1 ei ei+1 =ei+1
ei g ig i+1 =ei ei+1 =gi+1 gi ei+1
ei ej =ej ei
ei g j =gj ei

6.CONCLUSION:

I have tried to give a brief sketch of some of
the main ideas underlying the dynamically growing field of Brauer Centralizer Algebra. It is the natural Convergence of ideas from many areas of mathematics such as algebra, combinatorics, with those from computers science, such as algorithms, data structures. I feel confident that the current trend of studying Brauer Algebra will continue to suggest new classes of problems which are can continue for further enrichment of his knowledge.

7.Bibiliography:-

R.Brauer, On algebras which are connected with the semisimple continuous groups ann of
math.(2) 38(1937), 857-872.
P.Hanlon and D.B. Wales, On the decompositron of
Brauer’s centralizer algebras, J. Algebra 121 (1989),
409-445.
P.Hanlon and D.B.Wales, Eigen values connected with Brauer’s centralizer algebras, J.Algebra 121 (1989), 446-476.
IG.Macdonald, Symmetric functions and Hall polynomials, Oxford univ. press, London, 1979. H.wenzl, On the structure of Brauer’s centralizer algebras, Ann of math, 128(1988), 173-193.
I.S Luthar, I.B.S. passi, Algebra-Volume 3, Modules, Narosa Publishing house, 2005.
P.Hanlon and D.Wales, computing the discriminants of Brauer’s centralizer algebras, math comput. 54. No. 19(1990), 77-0796.