International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013

ISSN 2229-5518

COMPARATIVE STUDY OF HUFFMAN CODIN3G13 ,

SBAC AND CABAC USED IN VARIOUS VIDEO CODING STANDARS AND THEIR ALGORITHM

[1]Imran Ullah Khan

Research Scholar,
Dept. Electronics & Comm. Engg Mewar University, Mewar imranuk79@gmail.com

[2]M.A.Ansari, Senior Member IEEE Dept. Electrical Engineering, SOE Gautam Budha University, Gr. Noida ma.ansari@ieee.org

ABSTRACT

This paper represents the Algorithm for various

Coding standards such as Huffman coding, Syntax based arithmetic coding and Context Adaptive Binary Arithmetic Coding used in MPEG, H.263 and H.264 respectively and their analysis. We found that average bit per symbol (average code word length) for Huffman coding is nearly equal to Entropy which is the basic requirement, for different bit rate PSNR is calculated with and without SBAC and finally we discuss Block diagrams of CABAC codec of H.264/AVC and Modified parallel algorithm for CABAC. Experiments demonstrate that this SBAC provide the improvement of up to 1dB over conventional H.263. For a set of test sequences representing typical material used in broadcast applications and for a range of acceptable video quality of about 30 to 38 dB, average bit-rate savings of 9%-14% are achieved.

Key Words: CABAC, VLC, Transform Coefficient, DC

coefficient for INTRA blocks

I. VARIABLE-LENGTH CODING

A variable-length encoder maps input symbols to a
series of code words (variable length codes or VLCs). Each symbol maps varying length but must each contain an integral number of bits. Frequently- occurring symbols are represented with short VLCs whilst less common symbols are represented with long VLCs. Over a sufficiently large number of encoded symbols this leads to compression of data.

II. HUFFMAN CODING

In computer science and information theory,
Huffman coding is an entropy encoding algorithm used for lossless data compression.
The term refers to the use of a variable-length code table for encoding a source symbol (such as a character in a file) where the variable-length code table has been derived in a particular way based on the estimated probability of occurrence for each possible value of the source symbol. It was developed by David A. Huffman while he was a Ph.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes”[9].
Huffman coding assigns a VLC to each symbol based on the probability of occurrence of different
symbols. It is necessary to calculate the probability of occurrence of each symbol and to construct a set of variable length code words.

A.GENERATING THE HUFFMAN CODE TREE

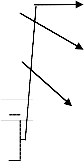
0.2 0.2 0.2

Figure 1: Huffman Code tree for Five Symbols

Table-1: Huffman Code for Five Symbols

Message	A	B	C	D	E
Probabilities	0.4	0.2	0.2	0.1	0.1
Code Word	00	10	11	010	011

The average bit per symbol (average code word length) is then

L = ∑ p i X Length of message in bits

i =1

L = 0.4 X 2 + 0.2 X 2 + 0.2 X 2 + 0.1 X 3 +
0.1 X 3 = 2.2 bits ……………………(1) Which is very close to the entropy given by

H(x) = −∑ p i log 2 p i ………. (2)

i =1

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013

ISSN 2229-5518

314

B. ALGORITHM FOR HUFFMAN CODING

1. List source symbol (messages) in the order of decreasing probability.

2. The two source symbols of lowest probability

are assigned numbers 0 and 1.

3. These two source symbols are combined Into a new message .

4. The probability of this new message is Equal to the sum of probabilities of the two original symbols.

5. The probability of this new message is Placed in the list according to its value.

6. Repeat this procedure until we are left with only two source symbols, for which a 0 and a 1 are assigned.

Figure 1 & 2 shows an example of Huffman Coding of five symbols, A-E. Their probabilities are shown in the second column. In the next column the two smallest probabilities are added and combined probability is included in the new order. The procedure continues to the last column, where a single probability 1 is reached. Starting from the last column for every branch of probability of a 0 is assigned to the top and a 1 in the bottom[9]. The corresponding codeword is read off by following the Fixed models are effective when the sequence from right to left. Although in fixed word length each sample is represented by three bits, they are represented in variable length code from two or four bits.

III. ARITHMETIC CODING

The entropy encoder converts a series of symbols representing elements of the video sequence into a compressed bit stream suitable for transmission or storage. An arithmetic encoder converts a sequence of data symbols into a single fractional number and can approach the optimal fractional number of bits required to represent each symbol[8].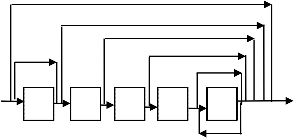

Block Layer

a b c d e

Figure 2 : H.263 Structure of SBAC Block layer

SBAC- Syntax based arithmetic coding
a-INTRADC- DC coefficient for INTRA blocks b- TCOF1 c- TCOF2 d- TCOF3
e- TCOF4
TCOEF-Transform coefficients

IV. SYNTAX BASED ARITHMETIC CODING

Huffman coding can be optimum if the symbol probability is an integer power of 1/2 which is usually not the case. Arithmetic coding is a data compression technique that encodes data by creating code string which represent a fractional value on the number line between 0 and 1[2]. It encourages clear separation between the model for representing data and the encoding of information with respect to that model. Another advantage of arithmetic coding is that it dispenses with the restriction that each symbol must translate into an integral number of bits, thereby coding more efficiently.
It actually achieves the theoretical entropy bound of compression efficiency for any source .
In other words arithmetic coding is a practical way of implementing entropy coding. There are two types of modeling used in arithmetic coding: Fixed model and adaptive model[5]. Characteristics of the data source are close to the model and have little fluctuation. In the adaptive model, the assigned probabilities May Change as each symbol is coded, based on the symbol Frequencies seen so far. Each symbol is treated as an individual unit and hence there is no need for a representative sample of text. Initially all the counts might be same, but they update as each symbol is seen.
A. DEFINING A MODEL
In general, arithmetic coders can produce near-optimal Output for any given set of symbols and probabilities (the optimal value is −log2P bits for each symbol of probability(P),compression algorithms that use arithmetic coding start by determining a model of the data basically a prediction of what patterns will be found in the symbols of the message. The more accurate this prediction is the closer to optimal the output will be

Example: A simple, static model for describing the output of

a particular monitoring instrument over time might be:
• 60% chance of symbol NEUTRAL
• 20% chance of symbol POSITIVE
• 10% chance of symbol NEGATIVE
• 10% chance of symbol END-OF-DATA For the four-symbol model above:
The interval for NEUTRAL would be [0, 0.6) The interval for POSITIVE would be [0.6, 0.8) The interval for NEGATIVE would be [0.8, 0.9)
The interval for END-OF-DATA would be [0.9,1)

B. ALGORITHM OF ARITHMETIC COING FOR ABOVE XAMPLE

The process starts with the same interval used by the encoder: [0,1), and using the same model, dividing it into the same four sub-intervals that the

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013

ISSN 2229-5518

315

encoder must have. The fraction 0.538 falls into the sub-interval for

(1) NEUTRAL, [0, 0.6); this indicates that the first symbol the encoder read must have been NEUTRAL, so this is the first symbol of the message.() Next divide the interval [0, 0.6) into sub- Intervals:

(2) The interval for NEUTRAL would be [0, 0.36) –

6 0% of [0, 0.6)

(4). The interval for POSITIVE would be [0.36,0.48)

20% of [0, 0.6)

(5). The interval for NEGATIVE would be [0.48,

0.54) - 10% of [0, 0.6)

(6). The interval for END-OF-DATA would be [0.54,

0.6). -- 10% of [0, 0.6).

7. Since .538 is within the interval [0.48, 0.54), the second symbol of the message must have been NEGATIVE.

Again divide our current interval into sub-intervals:
• The interval for NEUTRAL would be [0.48,
0.516)
• The interval for POSITIVE would be [0.516,
0.528)
• The interval for NEGATIVE would be [0.528,
0.534)
• The interval for END-OF-DATA would be
[0.534, 0.540).
Now .538 falls within the interval of the END-OF-DATA symbol; therefore, this must be the next symbol. Since it is also the internal termination symbol, it means the decoding is complete. If the stream is not internally terminated, there needs to be some other way to indicate where the stream stops. Otherwise, the decoding process could continue forever, mistakenly when all symbols have been encoded, the resulting interval unambiguously identifies the sequence of symbols that produced it. Anyone who has the same final interval and model that is being used can reconstruct the symbol sequence that must have entered the encoder to result in that final interval. A diagram showing decoding of 0.538 (the circular point) in the example model.
Consider the process for decoding a message encoded with the given four-symbol model. The message is encoded in the fraction 0.538 (using decimal for clarity, instead of binary; also assuming that there are only as many digits as needed to decode the message.) reading more symbols from the fraction than were in fact
encoded into it

Figure 3: Example for Arithmetic coding

V. OVERVIEW OF CONTEXT-BASED ARITHMETIC CODING (CABAC) IN H.264.

H.264/MPEG-4 AVC is the latest video compression standard that achieves the same video quality with almost half of the bit rate than previous video coding standards [1].
First a given non-binary value syntax element will pass to binarization to form a uniquely bin-string
.Second except for suffix of syntax element motion vector and level information, all of bins from binarization will enter into decision mode, and a probability model will be selected to assign context Model[14]. The selection of Probabilities models depends on previously encode syntax element or bins. After receiving bin an context, AC can encode and output the compressed data directly. AC can encode and output the compressed data almost half of the bit rate than previous video coding standards [1].
In which, the entropy coder, Context-based Adaptive Binary Arithmetic Coding (CABAC), plays an important role and can save, 9%~14% of bit rate in typical broadcast applications [15]. However, the design and implementation of the CABAC is difficult due to its inherent bit-serial nature. The coding result of one bit often has a direct effect on the coding process of the successive bits.
CABAC is used as one of the entropy coding method for H.264 video coding that is consisted of three stages Binarization, Context modeling and arithmetic coding (AC).First a given non-binary value syntax element will pass to binarization to form a uniquely bin-string .Second except for suffix of syntax element motion vector and level information[11], all of bins from AC consist of two sub-engines and is classified in three modes

(1) “Decision mode” that includes adaptive probability models and interval maintainer.

(2) “Bypass mode” for fast encoding of symbols.

(3) “Termination mode” for ending of encoding.

Successful entropy coding depends on accurate models of symbol probability. Context-based Arithmetic Encoding (CAE) uses local spatial and/or temporal characteristics to estimate the probability of a symbol to be encoded. Due to high correlation between the symbols in the image data, if the neighboring symbols of a, b, c are mainly 1 then it

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013

ISSN 2229-5518

316

START

Syntax
Bin String
Context
Modeler

Bitt Stream

Element

CABAC Encoder

CABAC Decoder

Binarizer

Binary Arithmetic

Coding Engine

Context 4
Modeler
Syntax
Element

Debinarizer

Bin String

Binary Arithmetic Decoding

Figure 4: Block diagrams of CABAC codec of 7

H.264/AVC
SE
Context index generation

read

Context memory

Binarization Probability update

9 10 13

Range table access
Binary Arithmetic coding
write

15 14

Bit-stream update

OUTPUT

BIT PACKING

Figure 5: Modified parallel algorithm for CABAC

Where SE-Syntax Element 21
AC-Arithmetic coding

STOP

Figure 6: CABAC Decoding Flow

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013

ISSN 2229-5518

317

Where
1 IS First MB of Slice

2 Initialization context memory & other CABAC

parameters

3 Determine Top/Left neighbor MBs for Current

MB
4 MB parameters initialize

5 Load info from global neighbor memory to local memories

6 Decode MB type and 8X8 type
7 IS skip MB?
Which is nearly equal to average bits per symbol (average code word length) =2.65 bits
(ii) The software for video codec used in this work is test model No.8 (TMN 8) version 3.0 developed by university of British Columbia Canada. This coder can accept
input video of various formats and includes almost all
options including that for advanced mode defined for
H.263 standard.
The tests are performed on standard video sequence SALESMAN” (QCIF,176x144,300 frames, 4:2:0 f ormat) The snapshot of this video sequence is shown in fig. (2).The performance is compared in terms of average Peak
signal to noise ratio (PSNR) using following relationship;
8 IS intra?
9 Decode IPCM MB

PSNR = 10 log ( 255 )2

10 MSE

= 20log ( 255 ) (for each Y, U, V)..................(6)

10 MSE

10 IS IPCM?
Where MSE is Mean square error

X Y

11 Read intra prediction mode

MSE =

1 ∑ ∑[i(x, y) − e(x, y)]2 ....................................(7)

12 Read chroma intra prediction mode
13 Read reference frame infromation
14 Read motion vector differential info
15 Read CBP info

XY x =1 y =1

Where i(x,y) = intensity of input pixel(for each Y,U,V)
e(x,y) = intensity of output pixel(for each Y,U,V)
The PSNR for entire video sequence is defined in terms of
average PSNR
16 Read transform flag info

Average

PSNR =

i ∑ PSNR(i)

(for each Y, U, V)..............................(8)

17 Read Delta quantization info
18 Read coefficient info
19 Store current MB info in global neighbor

t i =1

Where t is total number of frames in video sequence with each

memory

20 Package current MB info in global neighbor memory

21 IS last MB of slice
neighboring symbols are mainly 0 the assigned probability of x=1 should be reduced. Thus we can define the context for coding a 1 symbol as: Context=22c+21b+20a=4c+2b+a……………….…(3)
For the binary values of a,b,c the context has a value between 0 and 7. Higher values of context indicate a higher probability should be assigned for coding of 1.

VI. SIMULATION RESULTS

(i)The Entropy of the symbols which is the minimum average bits required to code the symbols can be calculate as;
frame of dimension XY and PSNR(i) is the PSNR value for i
frame and Y,U,V are standard luminance and chrominance
signals respectively.
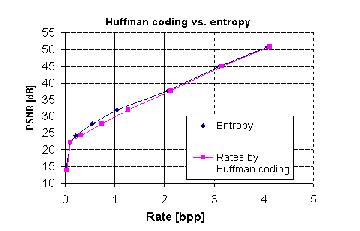
Table 2 gives the summary of results obtained for Huffman code and Entropy for various values of probability.
Table 3 gives the summary of results obtained in this work regarding the performance of H.263 video codec (Salesman sequence) for Syntax Based Arithmetic Coding at different target bit rates. It is observed that for SBAC improvement in PSNR is around 0.5 dB.

H ( x) = −∑ pi

i =1

log 2 pi

………….(4)

Figure 7: Snapshot of “Salesman” video sequence

H(x) == 0.4log2 (1/0.4) + 0.2log2 (1/0.2) + 0.2log2 (1/0.2)

+ 0.1log2 (1/0.1) + 0.1log2 (1/0.1)

= 2.1219.......(5)

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013

ISSN 2229-5518

318

Table 2: Entropy vs. Huffman codes

	Probabili ty	Average code word length(Huffman Code)	Entropy
1.	0.25	0.5	0.5
2.	0.20	0.4	0.45
3.	0.18	0.54	0.48
4.	0.15	0.45	0.42
5.	0.12	0.36	0.36
6.	0.06	0.24	0.244
7.	0.04	0.16	0.18

Table 3 : Simulation results for SBAC

S.No.	Without SBAC	With SBAC
	OBR (kbps)	PSNR (dB)	OBR (kbps)	PSNR (dB)
1.	20.05	30.18	20.05	30.22
2.	40.10	32.71	40.10	32.99
3.	60.14	34.91	60.14	34.95
4.	80.16	35.99	80.16	35.84
5.	100.23	37.47	100.23	37.53
6.	120.23	38.10	120.2	38.01
7.	140.24	39.23	140.24	39.65
8.	160.25	40.17	160.25	40.02
9.	180.27	41.41	180.27	41.15
10.	200.29	42.42	200.29	41.49

VII. CONCLUSION

In this paper we discuss the Algorithm for various Coding standards such as Huffman coding, Syntax based arithmetic coding and Context Adaptive Binary Arithmetic Coding used in MPEG, H.263 and H.264 respectively.
We found that average bit per symbol (average code word length) for Huffman coding is nearly equal to Entropy which is the basic requirement. For different bit rate PSNR is calculated with and without SBAC and there is a improvement of 0.02 – 0.5 dB with the use of SBAC.
Finally we discuss Block diagrams of CABAC codec of H.264/AVC and Modified parallel algorithm for CABAC.For a set of test sequences. Also the CABAC decoding flow diagram.

(a)

(b)

Figure 8:(a) Entropy vs. rates achieved by Huffman coding.

(b) Comparative performance of H.263 Coder

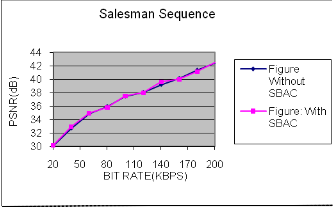
with and without SBAC Where BPP-Bit per pixel
PSNR-Peak Signal to Noise ratio

REFERENCES

[1] M.Ghanbari,”Video Coding: an introduction to standard codes;”IEE press, London 1999.
[2]Langdon G.G.An introduction to arithmetic coding IBM
journal, res. Develop, 28:2, pp.135-149, 1984. [3] www.ieee.org
[4] “ITU-T H.263 Encoder, version 2”,Signal Processing and Multimedia Group, University of British Columbia, Canada.
[5] http:\\www.ubvideo.com
[6]“Compressed video communications”, by Abdul
H.Sadka,published by John Wiley and sons, 2002. [7]R. Aravind, R.Civanlar, and A.R.Reibman,“Packet loss resilience of MPEG-
2scalable video coding algoriths,” IEEE Trans. Cirsuits and System video Technolology, vol. 6, pp.
426-435, Oct.1994

International Journal of Scientific & Engineering Research, Volume 4, Issue 11, November-2013

ISSN 2229-5518

319

[8] G. G. Langdon, “An introduction to arithmetic coding”, IBM Journal of Research and Development, Vol. 28, No. 2, pp.135-149 Mar. 1984.
[9] D. A. Huffman, “A method for the construction of minimum redundancy codes,”Proceedings IRE, vol.40, pp. 1098-1101, 1952.
[10] Draft ITU-T Recommendation and Final Draft International Standard of Joint Video Specification (ITU-T Rec. H.264/ISO/ IEC 14496-10 AVC), Mar.
2003
[11] Marpe. D, Schwarz. H, Wiegand. T, “Context- based adaptive binary arithmetic coding in the H.264/AVC video compression standard,” IEEE Transactions on Circuits and Systems for Video Technology, Volume 13, Issue 7, July 2003,p.p 620
– 636.
[12] Ha. V.H.S, W. S. Shim, and J. W. Kim, “Real- time MPEG-4 AVC/H.264 CABAC entropy coder,” in Internationa Conference on Consumer Electronics Digest of Technical Papers, p.p 255 - 256 , Jan. 8-12,
2005
[13] R. R. Osorio and J. D. Bruguera, “High- Throughput Architecture for H.264/AVC CABAC Compression System”, IEEE Transactions on Circuits and Systems for Video Technology, Vol.16, No.11, pp.1376-1384, Nov. 2006.