International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 807

ISSN 2229-5518

Behavior of Sierpinski Gasket Fractal Antenna

D.Pratap Varma, K.Phani Varma, Y.Srinuvas, V.Kalayan Raju, D.Prudhvi Raju

Abstract—the use of fractal geometries has significantly impacted many areas of science and Engineering one of which is antennas. Antennas using some of these geometries for various telecommunications applications are already available commercially. The use of fractal geometries has been shown to improve several antenna features to varying extents.

Yet a direct corroboration between antenna characteristics and geometrical properties of underlying fractals has been missing. This research work is intended as a first step to fill this gap.

In terms of antenna performance, fractal shaped geometries are believed to result in multi-band characteristics and reduction of antenna size. Although the utility of different fractal geometries varies in these aspects, nevertheless they are primary motives for fractal antenna design. For example, monopole and dipole antennas using fractal Sierpinski gaskets have been widely reported and their multiband characteristics have been associated with the self-similarity of the geometry.

Index Terms— Euclidean geometry fractal antenna, sierpinski, gasket, mono pole,

1. INTRODUCTION

——————————  ——————————

1.1 BACKGROUND

odern telecommunication systems require antennas with wider bandwidths and smaller dimensions than conventionally possible. This has initiated antenna research in various directions, one of which is by using fractal shaped antenna elements. In recent years several fractal geometries have been introduced for antenna applications with varying degrees of success in improving antenna characteristics. Some of these geometries have been particularly useful in reducing the size of the antenna, while other designs aim at incorporating multi-band characteristics. Yet no significant progress has been made in Corroborating fractal properties of these geometries with characteristics of antennas. The research work presented here is primarily intended to analyse geometrical features of fractals that influence the performance of antennas using
them.
Several antenna configurations based on fractal geometries
have been reported in recent years [1] – [4]. These are low profile antennas with moderate gain and can be made operative at multiple frequency bands and hence are multi- functional. In this work the multi-band (multifunctional) aspect of antenna designs are explored further with special emphasis on identifying fractal properties that impact antenna multi-band characteristics.
Furthermore, design equations for these antennas are
obtained in terms of its geometrical Parameters such as fractal dimension. Antenna properties have also been linked to fractal dimension of the geometry. To lay foundations for the understanding of the behaviour of such antennas, the nature of fractal geometries is explained first, before presenting the
status of literature on antennas using such geometries.

1.1.1 Fractal Geometries

The term fractal was coined by the French mathematician B.B. Mandelbrot during 1970’s after his pioneering research on several naturally occurring irregular and fragmentedgeometries not contained within the realms of conventional Euclidian geometry. The term has its roots in the Latin word fractus which is related to the verb fangere (meaning: to break). These geometries were generally discarded as formless, but Mandelbrot discovered that certain special features can be associated with them. Many of these
curves were recognized well before him, and were often associated with mathematicians of yesteryears. But Mandelbrot’s research was path-breaking: he discovered a common element in many of these seemingly irregular geometries and formulated theories based on his findings.

1.1.2 Engineering Applications of Fractals

Ever since they were mathematically re-invented by Mandelbrot, fractals have found widespread applications in several branches of science and engineering. Disciplines such as geology, atmospheric sciences, forest sciences, physiology have benefited significantly by fractal modelling of naturally occurring phenomena. Several books and monographs are available on the use of fractals in physical sciences. Fracture mechanics is one of the areas of engineering that has benefited significantly from the application of fractals.

1.2 Theory and design of small antenna

The quest for smaller sized resonant antennas has been on for decades. Several of antenna design principles may have to be modified while dealing with small-sized
antennas. By convention, a small antenna is defined as one occupying a fraction

International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 808

ISSN 2229-5518

(typically<1/6) of the wavelength [8]. The primary concern in their design is in the
impedance matching. This is better explained in the context of dipole antennas. As the length of a dipole antenna is reduced, the real part of its input impedance approaches zero, while the imaginary part tends to be an extremely large negative number. This causes major reflections at the input terminal as the transmission line connected to it generally has standard characteristic impedance (50Ω). The reactive part of the impedance is contributed by the induction fields in the near-zone of the antenna. The resistive part on the other hand may be attributed to various loss mechanisms present in and around the antenna, including the radiation “loss”. Losses due to the finite conductivity of the antenna structure, and that due to currents induced on nearby structures including ground contribute to the antenna input resistance.

2 SIERPINSKI GASKET GEOMETRY FOR MULTIBAND AND WIDEBAND ANTENNAS

The Sierpinski gasket is perhaps the most widely studied fractal geometry for antenna applications. Sierpinski gaskets have been investigated extensively for monopole and dipole antenna configurations [2]. The self-similar current distribution on these antennas is expected to cause its multi-band characteristics [6]. It has been found that by perturbing the geometry the multi-band nature of these antennas can be controlled. Variation of the flare angle of these geometries have also been explored to change the band characteristics of the antenna [5]. Efforts have also been made to improve the bandwidths of these antennas. A stacked antenna configuration with multiple layers of the fractal geometry has been found to be useful in this regard [7]. In addition, this configuration has been made conformal to improve the utilization of the antenna. Antennas using this geometry have their performance closely linked to conventional bow-tie antennas. However some minor differences can be noticed in their performance characteristics.The performance of these antennas is further affected by the nature and presence of dielectric supports. The effect of dielectric support on the antenna performance is studied using numerical simulations and the results are also included here.

3 SIERPINSKI GASKET FRACTAL GEOMETRY

Sierpinski gasket is one of the most common fractal geometries. The generation of this geometry is explained using formula. Although the geometry presented here consists of equilateral triangles, the description here holds good for any triangular geometry. One can explain its generation in two ways: the multiple copy approach, or the decomposition approach. In the first, one starts with a small
triangle. Two more copies of this triangle (same size) are generated and and attached to the original triangle. This process can be done n number of times, n being the order of the fractal iteration. In the decomposition approach, one starts with a large triangle encompassing the entire geometry. The
midpoints of the sides are joined together, and a hollow space in the middle is created. This process divides the original triangle to three scaled down (half sized) versions of the larger triangle. The same division process can be done on each of the copies. After n such divisions, the geometry shown in the figure is obtained.

Affine transformations, of which similarity transformations form a convenient sub-class, are important characteristics of fractal geometries. These involve scaling, rotation and translation. These transformations can be expressed in the mathematical form as:
In the above equation, r and s are scale factors, θand φcorrespond to rotation angles and x0 and y0 are translations involved in the transformation. If r and s are both reductions (r, s<1) or both magnifications (r, s>1), the transformation is self-affine. If r = s and θ=φ, the transformation is self-similar.

4 BASIC ANTENNA CONFIGURATIONS USING SIERPINSKI GASKETS

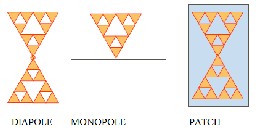
Several antenna configurations have been discussed in the literature using this geometry. These include monopole, dipole, patch and several variants of these [1], [2]. Some of these configurations are shown in Fig.1. In dipole and monopole configurations, the characteristics of the antenna have been qualitatively related to geometrical features of the underlying fractal patterns. Such a close relationship is hard to come by for the patch configuration, although this being conformal, has several aesthetic advantages from Applications point of view.

Fig. 1 Antenna configurations with fractal Sierpinski gasket

Two Sierpinski gaskets are printed on the ungrounded substrate so as to face each other at their apex, to form the dipole configuration. In this case, the feed is split between the two geometries. There is no ground plane present, making the antenna of low profile.

International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 809

ISSN 2229-5518

Dielectric materials similar to the previous case may be used. It may be noticed that the antenna configuration is very similar to a printed bow-tie antenna.

5 SIERPINSKI GASKET MONOPOLE ANTENNA

The schematic of a typical Sierpinski gasket monopole antenna is shown in Fig. 2. The antenna characteristics are studied both experimentally and numerically. A commercial finite difference time domain software (XFDTD) is used for numerical simulations.

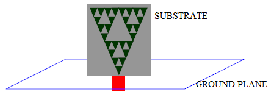
Fig. 2. Monopole antenna configuration with printed sierpinski gasket geometry

5.1 EFFECTS OF FRACTAL ITERATION LEVELS

Both numerical and experimental studies have been pursued to study the effects the
fractal iterations on the performance of the monopole antenna configuration. The substrate used in these studies was RT Duroid RO 3003, commercially available from Rogers Corporation, USA. This material has a dielectric constant of 3.0, and a thickness of 1.5 mm. In all cases, the total height of the geometry remained the same at 8 cm and apex angle at 60°. These geometries are shown in Fig.2. The simulated return loss characteristics of these antennas are shown in Fig. 4. It may be observed that the lower resonant frequencies of the antennas remain unperturbed by the increase in the iteration order. This is consistent with the physics of the geometrical resonance of the antenna structure. For example, the lowest resonance corresponds to the largest triangle, which remain the same in all cases. However, the remaining resonances
are higher order ones, which once again are controlled by the same dimensions. At
higher frequencies however the performance of these antennas differ, especially in their radiation characteristics.

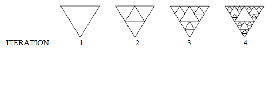
Fig.3 Different fractal interations studied for the antenna performance. The overall height in each case is kept at 8 cm. The apex angle is 60°.

The antennas are printed on a RO 3003 substrate for validation.

The measured return loss characteristics of the antennas fabrication is shown in Fig.5. As mentioned earlier, no specific trend in change in resonance can be deciphered from these curves. It is believed that the measured and simulated characteristics differ due to the effects of rectangular gridding used in the simulations. Such grids do not accurately
represent triangular geometries, especially at
intersections of triangles. The radiation
patterns are plotted at resonant frequencies of the
antenna (Fig. 6) also do not show
significant differences, except at higher resonances.
These patterns are shown in planes parallel and normal to
the plane of the geometry.

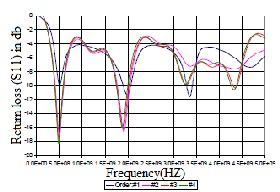
Fig. 4. Simulated return loss characteristics of the antenna

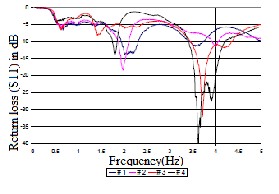
Fig 5. Measured return loss characteristic of the antenna printed on Duroid RO3003 substrate

International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 810

ISSN 2229-5518

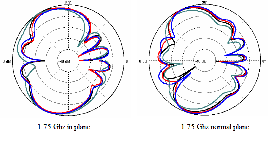
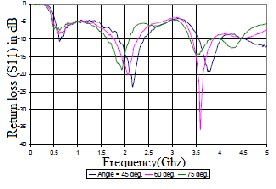
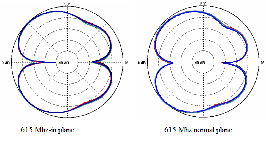
Fig.7 Measured return loss for fractal Sierpinski monopole antenna with different apex angles (where

the feed is connected). All geometries are of first iteration (simple triangles).

The above results indicate that multi-band characteristics of the simple triangular geometry itself can be modified by changing the flare angle. This, in effect throws into contention the statement that multi-band characteristics are

introduced by the selfsimilarity of the fractal geometry [6].

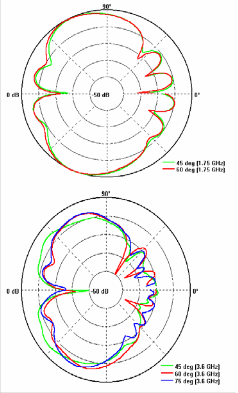
Fig 6. Radiation patterns of Sierpinski gasket monopole antenna for four different iterations of the Geometry. The patterns are measured at

615 MHz and 1.75 GHz and 3.6 GHz in an anechoic chamber. Patterns at two orthogonal planes are plotted, in planes parallel and normal to the geometry.

5.2 EFFECTS OF APEX ANGLES

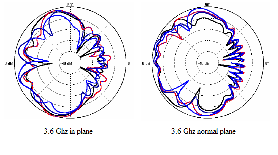
A similar approach is also followed to study the effect of changing the apex angle on the antenna performance. Changes in flare (apex) angle have been reported to change the Multi-band characteristics of the monopole antenna using Sierpinski gaskets [5]. In the present paper, all models are of the same height, and only the first iteration geometry (solid triangle) is used in this comparison. The angles studied are 45°, 60°, and 75°. The measured characteristics are compared in Fig.7. These indicate a characteristic shift in resonance towards the lower side, as the angle is increased. Radiation patterns for these antennas in a plane along the geometry is shown in Fig.8.

Fig. 3.10 Radiation patterns of triangular monopole antenna for different flare angles. The patterns are

measured at and 1.75 GHz and 3.6 GHz in an anechoic chamber. Patterns in the plane parallel to that of the geometry are plotted.

International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 811

ISSN 2229-5518

6 CONCLUSION:

The aim of this paper to show how the fractal antenna (sierpinski gasket) behaviour changes according to change iteration and apex angle of physical design. As we observed in the simulation results lower frequency of the antennas remain unpredictable by increasing in the iteration order. As flare angle increases, a characteristics shift in resonance towards the lower side.

REFERENCES

[1] C. Puente, J. Romeu, R. Bartoleme, and R. Pous, “Fractal multiband antenna based on Sierpinski gasket,” Electron. Lett., vol. 32, pp. 1-2, 1996.

[2] C. Puente-Baliarda, J. Romeu, R. Pous, and A. Cardama, “On the behavior of the Sierpinski multiband fractal antenna,” IEEE Trans. Ant. Propagat., vol. 46, pp. 517- 524, 1998.

[3] N.Cohen, “Fractal antenna applications in wireless telecommunications,” in Professional Program Proc. of Electronics Industries Forum of New England, 1997, IEEE, pp. 43-49, 1997.

[4] C. Puente-Baliarda, J. Romeu, R. Pous, J. Ramis, and A. Hijazo, “Small but longKoch fractal monopole,” Electron. Lett. vol. 34, pp. 9-10, 1998.

[5] C. Puente, M. Navarro, J. Romeu, and R. Pous, “Variations on the fractal

Sierpinski antenna flare angle,” IEEE-APS International Conf. IEEE, pp.

2340-2343, 1998.

[6] M. Navarro, J.M. Gonzalez, C. Puente, J. Romeu, and A. Aguasca, “Self- similarsurface current distribution on fractal Sierpinski antenna verified with infra-red thermograms,” IEEE-APS International Conf. IEEE IEEE, pp. 1566-1569, 1999.

[7] M. Navarro, J.M. Gonzalez, C. Puente, J. Romeu, and A. Aguasca, “Self- similar surface current distribution on fractal Sierpinski antenna verified with infra-redthermograms,” IEEE-APS International Conf. IEEE IEEE, pp. 1566-1569, 1999.

[8] H.A. Wheeler, “Small Antennas,” IEEE Trans. Ant. Propagat, vol. AP-23,

pp. 462- 469, 1975.