International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 626
ISSN 2229-5518
1 Achish R.A Robin 2 R.Rajesh kanna
OFDM is the multi carrier modulation system. In scheme large numbers of equalizers are used at receiver which increases the overhead and cost of the system.OFDM uses Fast Fourier transformer (FFT) and Inverse Fast Fourier Transformer (IFFT) to replace modulation and de- modulation. Orthogonal Frequency Division Multiplexing (OFDM) has been proposed for use in millimeter-wave transmission systems. This is due to OFDM having superior performance over single carrier system in multi-path wireless channels. The OFDM allows the transmission of the data over multiple orthogonal subcarriers, created by the mean of a Fourier Transform; each subcarrier is modulated independently resulting in a narrow band signal that will only experience the effects of flat fading.The orthogonally of the subcarriers ensures the OFDM modulation scheme is spectrum efficient. In recent years, Field-Programmable Gate Arrays (FPGAs) have become a key component for implementing high performance digital signal processing (DSP) designs particularly for digital communication systems.In singlecarrier system signalrepresenting each bit uses the entire available spectrum. Orthogonal frequency division multiplexing (OFDM) is an effective transmission scheme to combat multipath fading[1].
1 Achish R.A. RobinM.E Applied ElectronicsHindusthan
College of Engineering and Technology
2 R.Rajesh kannaAssistant Professor, Hindusthan College of
Engineering and Technology, India
The primary advantage of OFDM over single-carrier schemes is its ability to cope with severechannelconditionswithout complex equalization filters. Channel equalization is simplified because OFDM may be viewed as using many slowly modulated narrowband signals rather than one rapidly modulated wideband signal. The low symbol rate makes the use of a guard interval between symbols affordable, making it possible to eliminate inter symbol interference (ISI) and utilize echoes and time-spreading (on analogue TV these are visible as ghosting and blurring, respectively) to achieve a gain, i.e. a signal-to-noise ratio improvement. This mechanism also facilitates the design of single frequency networks (SFNs), where several adjacent transmitters send the same signal simultaneously at the same frequency, as the signals from multiple distant transmitters may be combined constructively, rather than interfering as would typically occur in a traditional single-carrier system.
Orthogonal Frequency Division Multiplexing (OFDM)
has been proposed for use in millimeter-wave transmission systems. This is due to OFDM having superior performance over single carrier system in multi-path wireless channels[6]. The OFDM allows the transmission of the data over multiple
IJSER © 2014
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 627
ISSN 2229-5518
orthogonal subcarriers, created by the mean of a Fourier Transform; each subcarrier is modulated independently resulting in a narrow band signal that will only experience the effects of flat fading[2]. The orthogonally of the subcarriers ensures the OFDM modulation scheme is spectrum efficient. In recent years, Field-Programmable Gate Arrays (FPGAs) have become a key component for implementing high performance digital signal processing (DSP) designs particularly for digital communication systems[3].
The FFT processor is a very important component in Orthogonal Frequency Division Multiplexing(OFDM) system. In this paper, we propose an ancient variable-length radix-8/4/2 FFT architecture. The FFT processor is generally based on radix-8 FFT algorithm which also supports radix-4 or radix-2 FFT computation. The pipelined radix-8/4/2 buttery unit computes radix-8 FFT algorithm basically. For the limitation it cannot run radix-8 FFT algorithm in the last stage as it computes radix-4 or radix-2 FFT algorithm. The proposed FFT architecture uses shared-memory to minimize and simplify a hardware. We are using e cient In-place memory access method to maintain conict-free data access. Also we can replace a very large lookup table with a twiddle factor generator which consumes less area then a ROM- based lookup table.
An Efficient FFT processor should not only provide a high throughput rate, but also deal with the multiple data sequences effectively for MIMO OFDM application[5] .In our view, the pipelined architecture should be the best choice for the high throughput rate applications since it can provide high throughput rate with acceptable hardware cost .The pipelined FFT architecture typically falls into one of the two following categories. One is multipath delay commutation feedback (MDC) and the other is single path delay feedback (SDF) . In general the MDC scheme can achieve higher throughput rate by using multiple data paths, While SDF scheme needs less memory and hardware complexity with delay feedback scheme .Besides , the operation of the complex multiplication consumes lots of power in the FFT processor. In order to save power dissipation, higher radix FFT algorithm can be used to reduce the number of complex multiplications . Three-step radix-8 FFT algorithm is chosen in our design to save complex multiplications.
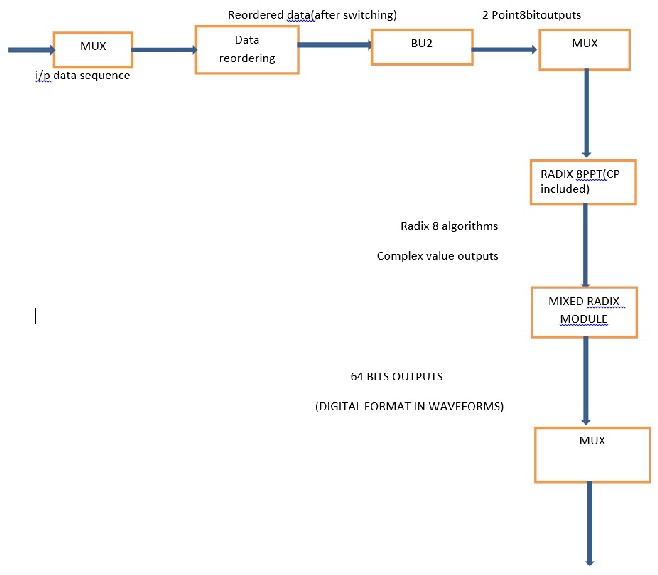
Data re-ordering contains several different-size delay elements and a switch block. The function of Data re- order is to reorder the input sequences to achieve parallel processing and to let output to the next block.The re- ordered data will be separated into 32 groups or 16 groups for 128- or 64-point, respectively. Each group contains four
data sequences, A, B, C, and D. And each data sequence in the same group has the same FFT index. In general, the operation of the FFT is data dependent. In order to implement the multiple data sequences more efficiently, separate the data into several groups[7]. The group replacing the FFT index the 128-point mixed-radix FFT algorithm in our design. Because each data sequence in a group has the same becomes the basic unit of the FFT operation.
The four complex multipliers are needed in the four-parallel approach to implement a radix-2 FFT algorithm. In this work, a group concept is used to deal with multiple data sequences and only two complex multipliers are used in this module. A block diagram of Module 2 consisting of a memory, 4 butterfly units of radix-2 FFT algorithm (BU_2), two ROMs, two complex multipliers, and some multiplexers.
If 64-point FFT/IFFT is operated in our scheme, the data will skip this module[8]1. The memory size can store the data of 16 groups containing 256 complex data. Because four data paths are adopted in our design, four memory banks are needed to provide four data from memory to BU_2 simultaneously. Only1/8 period of cosine and sine waveforms are stored in ROM and the other period waveforms can be reconstructed by these stored values. The operation of BU_2 is complex addition and complex subtraction from two input data.
Because radix-2 FFT algorithm is adopted in this
module, BU_2 can not start until both input sequences x(n) and x(64+n), when n=0,1,2……63 are available. According to the group data format, the data of the first 16 groups are stored in the memory. When the data of the next 16 groups enter Module 2, the eight input data are loaded into four from the memory four from BU_2s, and four from the input, respectively. The operation of BU_2 in a group is dependent tO the number of the data in a sequences.
In four-parallel approach, the utilization rate of the complex multiplier is only 50%. The proposed approach can increase the utilization rate and reduce the number of complex multipliers. The detailed operation is described below. Four output data must be generated after BU operation. Two of
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 628
ISSN 2229-5518

Fig:1.1
These smaller DFTs are combined via size-r butterflies, which themselves are DFTs of size r (performed m times on corresponding outputs of the sub-transforms) pre-multiplied by roots of unity (known as twiddle factors). (This is the
The butterfly unit is a portion of the computation that combines the results of smaller discrete Fourier transforms (DFTs) into a larger DFT, or vice versa (breaking a larger DFT up into sub transforms). The name "butterfly" comes from the shape of the data-flow diagram in the radix-2
. The same structure can found in the Viterbi algorithm can used for finding the most likely sequence of hidden states.
Most commonly, the term "butterfly" appears in the context of the Cooley–Tukey FFT algorithm, which breaks
down a DFT of composite size n = rm into r smaller transforms of size m where r is the "radix" of the transform.
"decimation in time" case; one can also perform the steps in reverse, known as "decimation in frequency", where the butterflies come first and are post-multiplied by twiddle factors.
The operations of BU_2(radix 2) of each stage, which is the same as that of BU_2 in Module 2 shown in Fig.4, are the complex addition and the complex subtraction. For example, the data of the first 8 groups are stored in the delay elements in the first stage of radix8. When the data of the next groups are valid from the input, eight data are processed to four BU_2s from both the input and the delay element. The
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 629
ISSN 2229-5518
output data generated by the BU_2 in the first stage or second stage are multiplied by a trivial twiddle factor before they are fed to the next stage. These twiddle factors can be implemented efficiently. But the output data from the third stage of radix 8 need to be multiplied by the nontrivial twiddle factors simultaneously in the modified complex multiplier as in fig1.2.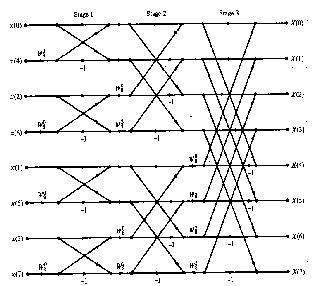
Fig:1.2
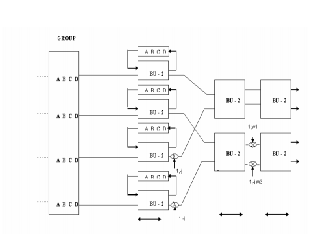
The architecture of Radix 8 is directly mapped from 3-step radix-8 FFT algorithm. Four identical components are used in each stage since four-parallel approach is adopted. In our design, four input data are loaded into Radix 8 from the previous module simultaneously. The different data sequences A, B, C, and D are considered as a group. The size of the delay element in three stages is 32 (8 group), 16 (4 group) and eight (2 group), respectively. The function of delay element is to store the input data until the other available input data is received for the BU_2 (radix 2) operation.
Fig:1.3
two available data of the BU_2(radix 2) in the second stage and third stage are in the different data paths as in fig 1.3. So the structure of Module 4 is modified to ensure that the FFT output data are correct. Some output data generated by the BU_2 in the first stage and second stage are multiplied by the nontrivial twiddle factors before they are fed to the next stage.
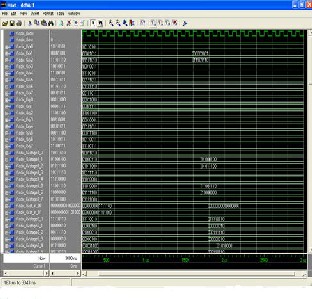
Fig:1.4
In Fig:1.4 Orthogonal frequency division multiplexing communication systems are extremely sensitive to frequency synchronization errors as compared to single carrier systems [9]. OFDM is very sensitive to frequency offset errors which damages orthogonally among subcarriers and introduce Intercarrier Interference (ICI).Therefore, Carrier frequency offset (CFO) estimation in OFDM systems is required to improve system performance as shown in Fig 1.5
Three-step radix-8 FFT algorithm is realized in the final block There are also three stages in Mixed radix to implement three-step radix-8 FFT algorithm. The scheme of the Mixed radix is different from that of radix 8 because the
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 630
ISSN 2229-5518
Fig1.5
In this Paper, the 64-point and 128-point FFT/IFFT Implemented. Based on the concept of data reordering and grouping, the processor can provide different throughput rates to deal with 1–4 simultaneous data sequences more efficiently. Due to this design the hardware costs of memory and complex multipliers are saved. And the number of complex multiplications can be reduced effectively by using higher radix FFT algorithm. Due to reduced hardware the power consumption also low. The technique of the MIMO increased the data rate by extending an OFDM –based system.
[1] Performance—Complexity Comparison of Receivers
for a LTE MIMO–OFDM System JohannaKetonen,StudentMember,IEEE,MarkkuJuntti,Se niorMember,IEEE,andJosephR.Cavallaro,SeniorMember
,IEEE.
[2]Low Power Detection Architecture for MIMO Systems.ShirlyEdward.A,Malarvizhi.S,Anjana.R,Aishwa rya.R Department of ECE,SRM University,Vadapalani,Chennai,India.
[3]OFDM System With Carrier Frequency Offset Estimation Using Complex Training Symbol. MeghashreeD.Nimje*, A.P.Rathkanthiwar
[4]PAPR Reduction of OFDM Using PTS and Error- Correcting Code Sub blocking
..AbolfazlGhassemi,StudentMember,IEEE,andT.AaronG
ulliver,SeniorMember,IEEE
[5]System Design and Analysis of MIMO SFBC CI- OFDM System against the Nonlinear Distortion and Narrowband Interference. Heung-GyoonRyu Member, IEEE
[6]Intercarrier Interference Immune Single Carrier OFDM via Magnitude-Keyed Modulation for High Speed Aerial Vehicle Communication..XueLi,StudentMember,IEEE,StevenHo ng,StudentMember,IEEE,VasuD.Chakravarthy,Member, IEEE,
[7]A Comparison of Frequency-Domain Block MIMO TransmissionSystems… RezaKalbasi,Member,IEEE, DavidD.Falconer, Life Fellow, IEEE,
[8] M.J. Canet, F. Vicedo, V.Almenar, J. Valls, “Fpga implementation of an if transceiver for OFDM-based WLAN”, in IEEE Workshop on Signal Processing Systems, 2004. (SIPS 2004), 2004, pp.227-232
[9] F. Manavi and Y.R. Shayan, “Implementation of OFDM modem for the physical layer of IEEE 802.11a standard based on Xilinx Virtex-II FPGA” in 59th IEEE Vehicular Technology Conference ( VTC 2004) 2004, pp.
1768-1772.
[10]F. Poegel, S. Zeisberg, A. Finger, “Comparison of different coding schemes for high bit rate OFDM in a 60
GHz environment”, in IEEE 4th International
Symposium on Spread Spectrum Techniques and
Applications Proceedings,vol.1, 22-25 Sep 1996, pp. 122
– 125.
[11] A. Sghaier, S. Areibi, B. Dony, “A pipelined implementation of OFDM transmission on reconfigurable platforms” in Canadian Conference on Electrical andComputer Engineering, (CCECE 2008),
2008, pp. 000801-000804.
[12] IEEE 802.15 WPAN Task Group 3c (TG3c) Millimeter Wave Alternative PHY Friday, 5 February
2010, [Online]. Available:http://www.ieee802.org
/15/pub/TG3c.html
IJSER © 2014 http://www.ijser.org