International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 217

ISSN 2229-5518

An analytical model of the transient thermal behaviour of semiconductor device

Marija Radmilović-Radjenović, Branislav Radjenović

Abstract— In this paper, an analytical one dimensional mathematical model of the transient thermal behavior of semiconductor devices is pre- sented. The regions where the heat is dissipated are modeled as δ(x) source located at finite distance beneath the top surface. Three procedures including Fourier and Laplace transforms as well as Fourier series, for obtaining an explicit expression for the temperature space-time depend- ence are described in details. Simple analytical relations for the transient thermal impedance andthermal time constants are derived. It is shown

that temperature time dependence can be described with only one parameter – rise time

ance has the same form as that obtained using the phenomenological model.

τ r . Simple analytical expression of the thermal imped-

Index Terms— thermal, transient, p-n junction, semiconductior, device, MOFSTE, transform.

——————————  ——————————

1 INTRODUCTION

T is well known that the thermal system optimization plays very important role in electrical optimization. For example, with decreasing size and growing complexity of micro- electronic and micro-electro-mechanic systems(MEMS), the power dissipation of integrated circuits has become a critical concern. Thus, the thermal analysis of microelectronic devices has been the object of increasing interest for last several years. The problem of dissipating from digital to analog circuits and power devices [1]-[3]. Undesirable effects such as thermal runway, thermal coupling between neighboring devices, sub- strate thinning, multilayer substrates, surface metallization, etc., unfavorably affecton the performance of semiconductor devices and circuits. Most published papers related to these problems assuming steady-state conditions [4]-[9], while rela- tively few of them deal with the transient thermal modeling of microelectronicdevices [10], [11]. However, with growing a number of applications, the transient thermal behavior of in- tegrated devices remains a critical issue. Since this phenome- non strongly affects the maximum dissipated power it isvery important to determine the thermal constants that correspond to the temperature rise and hot spot formation under pulsed-
power conditions.
In order to characterize the dynamical thermal behavior,
semiconductor manufactures usually provide transient ther-
mal impedance curve Zth(t) which shows the time dependence
of the ratio of the peak temperature and dissipated powerfor a step application of constant power [12]. Often it is necessary
to determinethe thermal behavior precisely in the microsecond time scale, which additionally complicates measurements. Either numerical [13], [14] or analytical [12], [15]-[17] ap-

————————————————

• Marija Radmilović-Radjenović is currently at the Institute of Physics, University of Belgrade, Pregrevica 118, Belgrade, Serbia, . E-mail: mari- ja@ipb.ac.rs

• Branislav Radjenović is currently at the Institute of Physics, University of

Belgrade, Pregrevica 118, Belgrade, Serbia, . E-mail: bradjeno@ipb.ac.rs
proaches have been developed to solve this problem. In par ticular, modern trend of describing complete devices by mod- els involving two or three spatial dimension provides that the consideration of the time dependenceof the transient thermal impedance is inevitable. Unfortunately, a limited amount of analytical expressions of the thermal time constants which incorporate the three-dimensional nature of the heat flow and the physical structure of the device exists [12].
Different techniques that have been developed lead to a computationally intensive implementation but do not allow for a deeper physics insight [12]. There are two principle ap- proaches to simulate electro-thermal behavior of integrated circuits – the direct method and the relaxation method [13]. The direct method is based on modelling the thermal and elec- tronic behavior of the circuit for a single simulation tool [18]. The relaxation method is based on the coupling of a thermal and a circuit simulator [19], [20].
Numerical methods, usually computationally very expen-
sive, do not lead to clear understanding of the transient ther- mal response and do not allow for a simple derivation of the characteristic time constant. So, analytical solutions are need- ed. Analytical studies of the transient thermal behavior usual- ly include rough estimates of the characteristic time constants based on the so-called ”thermal capacitance” concept [15] and simplified solutions for the one-dimensional case [16,17]. One of these is method of images [22] which uses ”Green function” to represent the temperature distribution resulting from a point heat source. However, most analytical solutions are based on Fourier expansions or Laplace transforms. Besides the fact that these Fourier solutions are limited by the number of layers, all analytical solutions are forced to assume a con- stant heat conductivity which reduces the problem into solv- ing the linear transient heat flow equation [14]. More accurate solutions obtained taking into account the tree-dimensional nature of the heat flow have been derived in the form of a

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 218

ISSN 2229-5518

Fourier series [11] or a convolution integral, although these approaches do not provide a simple derivationof the charac-
teristic time constant.
and an initial condition:

Θ(x,0) = 0,

(4)
In this paper, a simple analytical relation for the transient
where α

= λ / cρ is the thermal diffusivity, λ is the ther-

thermal impedance curve based on the Fourier series ap- proachis derived. The proposed solution provides a good physical description of the phenomenon and is in very good agreement with the expression derived by coupling the elec- trical model of a component with the description of its thermal properties using an electric analog model [17].

2 DESCRIPTION OF A MODEL

It is well known that many properties of power semiconduc- tors are strongly temperature-dependent. A maximum junc- tion temperature is specified for all semiconductor compo-
mal conductivity of substrate, c is the specific heat, ρ is the
density of the semiconductor material and x describes the co- ordinates in the direction of heat propagation. P g(x,t) is the volume density of dissipated power and we shall assume in following that the thickness of dissipating region is negligible.

This assumption is reasonable for MOSFET and MESFET de- vices, but can questioned for bipolar transistors when volume heat source model is more appropriate. This assumption means that dependence of the function Pg (x,t) on the spatial coordinate and on the time can be resolved separately, or the function Pg (x,t) can be expressed as:

nents, when exceed, can lead to destruction or permanent-

P (x, t ) = P

δ (x) f (t ) , (5)

damage of the component. Even when temporary events such g gS
as avalanche or short-circuit conditions take place, it must be
where the function

f (t )

describes time dependence of the
ensured that the maximum permissible junction temperature
is not exceeded.Within the safe operating range, the life time
of semiconductor components is strongly affected by tempera- ture fluctuations due to loading. Each change in temperature causes mechanical stress in the component causes solder and- bond connections. Here, it is not the absolute temperature which is decisive, but the temperature cycling. As a rule of thumb, it can be assumed that the aging of a component is proportional to the fourth power of the temperature deviation. In a MOSFET, increasing of temperature induces the drop of the breakdown voltage and consequently reduces the signal- to-noise margin at the control mode. Increasing of the temper- ature also provides increasing of the conduction losses. Ignor- ing these effects can lead to un undesired- turn-on of the tran- sistor when it should be inhibited.
In this paper we consider an improved version of the sim- ple analytical on edimensional (1-D) model presented earlier [16], [17]. Geometry of the devices is shown in Figure 1. The heat source (shaded region) is located at the distance D be- neath the top surface, at which the adiabatic condition is as- sumed. At the bottom of the device (x = L) the heat convection condition is proposed. In general, the propagation of heat in a system can take place in three different ways, convection, heat radiation or heat conduction. Bearing in mind that electronic components usually have only heat conduction, in our analy- sis we start with one dimension heat transfer equation:

power dissipation. So, the problem we are solving is defined by eq. (1), boundary and initial conditions (2)-(4) and the as- sumption (5).

Fig. 1. Schematic view of a structure with p-n junc- tion in the middle.

3 INTEGRAL TRANSFORMS

The most general technique of solving inhomogeneous boundary problem is to use methods of integral transforms. In the following we shall briefly discuss the possibilities of such approaches.should not be selected.

3.1 Laplace transforms

Applying Laplace transform to eq. (1) we obtain an ordinary differential equation for space dependence of temperature function:

∂ 2 Θ 1

−

∂x 2 a 2

∂Θ = −

∂t

Pg (x, t )

(1)

d 2 

(x s )

s  ( )

gs ( )  ( )

with boundary conditions:

Θ ,

dx 2



− Θ x, s

a 2

= − δ x f s ,

λ2

(6)

∂Θ = 0, for x = -D, (2)
where

f (s)

is Laplace transform of

f (t ). The solutuion of

∂x

∂Θ = α

∂x λ

Θ, for x = L, (3)
eq. (6) can be written in the form:

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 219

ISSN 2229-5518

   

(7)
pendent case as a sum of two terms:

Θ(x, s ) = C exp(−

s x)+ C exp( s x)− aPgs f (s )sh

s x h( x).

1 2 s  a 

Complex constants C1 and C2 can be determined from the boundary conditions (2):

Θ(x, t ) = Θ h (x, t ) + Θ(x, ∞)

(12)

 

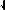
where Θ

(x, t ) is the solution of homogenous problem with

aPgs



exp



s (2D + L) s

a 



ch



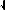
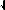
s   s

L  

a 



ch

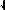
s  a

a L  + λ



sh

s 

a L  h

  

=  ( )

  

 ,

C f s

λ s

a − s 

λ a 

  

 exp 2 

  

additional constraint

 

C2 = C1 exp − 2 

 a 

Θ h (x,0) = −Θ(x, ∞),

(13)

3.2 Fourier transform

originating from the initial condition

Θ(x,0) = 0 . Homoge-

Applying them on eq. (1), we get system of coupled equations:
nous solution

Θ h (x, t ) can be expressed as well known infi-

=d 2Θ( x,ω

) =ω ( ,ω )

Pgs δ ( ) (ω ),

nite series:

dx2

+ a2 C x

= − x f

λ s

(9)

Θ (x, t ) = ∑ exp(− γ 2α 2 t )[A cos(γ

x) + B

sin(γ

x)],

(14)

=d 2 Θ( x,ω

) =ω ( ,ω )

Pgs δ ( ) (ω ),

(10)

n =0

n n n n n

dx 2

− a 2 C

= − λ x fC
where constants An and Bn and eigenvalues γ n have to be de-
where with subscripts S and C Fourier sine and cosine trans-
termined from boundary and initial conditions. From the
forms are denoted, respectively. The solution of this system
are real functions given by relatively simple formulas:
boundary conditions the equation defining
tained:

γ n can be ob-

Θ (x, ω ) =

a  1

sh

ω x  2 ω sin 1

ω x C +

2 cos 1

ω x 

− C −

gs ( f (ω ) − f (ω ))h(x) +

α cos(γ

L) − γ

sin(γ L)

 

s   

  

  4 

 P

C2 1 C s  n n n

(15)

2 ω   a

2  a

 a a 

 a a  λ



tg (γ

n D) =

λ .

+ ch 1

ω x  2 ω cos 1

ω x C +

2 sin 1

ω x 

+ C −

gs ( f (ω ) − f (ω ))h(x)

sin(γ n L) + γ n cos(γ n L)

 



 a  a

 

 a a  3



 a a



C1



2 λ C s



 ,

Θ (x, ω ) = a

  1

ω x  2 ω cos 1

ω x C +

2 sin 1

ω x 

− C −

gs ( f (ω ) − f (ω ))h(x) +

 

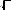
C ch 

  

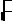
  4 

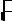
 P

C1 2 s C

 Constants An

and Bn can be obtained from the boundary con-

2 ω   a

2  a

 a a 

 a a  λ



ditions x = -D and initial condition (6):

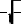
 1

+ sh

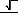
ω  2

x −

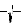
ω  1 sin

ω 

x C +

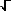
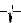
 1

2 cos

ω 

x  C + C −

Pgs

( f (ω ) + f (ω ))h(x)

An = −Bn ctg (γ n D),

(16)

 

 

  3

 

  1

 

2 λ C s





Integration constants C1 , C2 , C3 and C4 are real numbers and can be determined from the conditions (2)-(4), but the result-

B = −

Θ(x, ∞)[sin(γ x) − ctg (γ D)cos(γ x)]dx = PgS ctg (γ D).

(17)

n ∫

ing expressions are too complicated to be presented here. Un- − D
like of the case of the Laplace transform, inverse sine and co-

n n n

λγ 2 n

sine transforms are defined as real integrals on the positive part of the ω axes. The main problem in their numerical evalu- ation is singular behaviour of the functions defined by (17) or
Fanally, combining the expressions above we get the expres-
sion defining thermal impedance:
(18) at ω = 0 point.

Z (t ) = =Θ(0, t )

1  1

= 

L  1

 −

∑ 1 ctg

2 (γ D)exp(− 

(18)

3.3 Fourier series

SPgS

S  α

λ  λ n =0 γ n 

The Fourier series approach is probably the most common way of solving problems based on heat transfer equation [12]. In its original interpretation homogenous form of the equation is supposed. To deal with the heat source (the right side) of the equation (1) we assume that the time dependence of it is given by the Heaviside unit step function: f(t) = h(t) . In that case, the stationary solution of the boundary value problem (1)-(4) is given by the simple relation:
The expression (18) for the thermal impedance has a mathe- matically simple closed-form which is the same observed in [23] derived using the phenomenological model. Since the same forms of the expressions of the thermal impedance ob- tained using two different approaches: Fourier series approach (this paper) and the phenomenological model [23] allow us to conclude that our simple analytical model provides a good physical description of the transient thermal behavior of semi-

  conductor device.

Θ(x, ∞) = P

 + [L − xh(x)].

(11)

gS α λ 

With this, it is possible to write down solution of time de-

4 RESULTS

Although the relation (18) has a simple form, it could be
greatly simplified when

D → 0 . Equation (18) then becomes

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 220

ISSN 2229-5518

γ n tg (γ n L) = α / λ

and its smallest zero is simply γ 2 ≈ α /(λL).

ance with the single parameter- rise time . Our analytical ex-
The same relation leads to approximate value of the coeffi-
pression derived by using Fourier series approach has the
cient ctg 2 (γ

D) ≈ γ 2 (L + λ / α )

also and retaining the first
same form as that obtained by using the phenomenological
model, which confirms the accuracy of our procedure. Our
term in (18) only, we get the final straightforward expression
for thermal impedance:
derivation is most elegant and simple in comparison with very robust derivation described in [12], we may conclude that the

 L 

 t  cρ

method that we suggest represents a simple and very effective

Z th

(t ) = 1  1 +

1 − exp −

, τ r

= L .
(19)
approach to the transient thermal behavior problem. Having

S  α

λ 

 τ r  α

in mind that the thermal behavior of practical solid state de- vices may be strongly affected by complex effects such as sub-
So that, we have shown that it is possible to describe the dy-
namic of the thermal response with one parameter only-rise time τ r . In the case when D cannot be neglected it would be

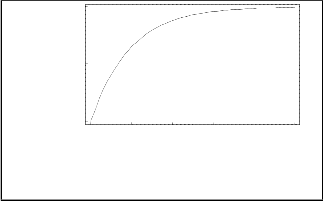
difficult to derive similar relation, but one must remember that relation D<<L always holds. The exponential time de- pendence of the Zth is shown in Figure 2, while the tempera- ture profile is shown in Figure 3.

Zth

0.5

0 10 20 30 40 50

t[s]

Fig. 2. The time dependence of the termal impedance.

Fig.3. Temperature profile.

5 CONCLUSIONS

In this paper we have described an improved version of a simple model of the transient thermal behavior of semicon- ductor devices and described three promising methods of finding its analytical solution. Also, we have shown that it is possible to describe transient behavior of the thermal imped-
strate thinning, multilayersubstrates, surface metallization, oxide isolation etc., these effects will be tasks of our future works.

ACKNOWLEDGMENT

This work was supported by the Ministry of Science and
Technology.

REFERENCES

[1] V. Szekely, M. Rencz and B. Courtois, “Tracing the thermal behavior of ics,” IEEE Des. Test. Comput., vol. 15, pp. 14-21, . 1998.

[2] R.M. Fox, S. Lee and D.T. Zweidinger, “The ef- fects of BJT self- heating on circuit behavior,” IEEE J. Solid-State Circuit., vol. 28, pp.

678-685, . 1992.

[3] B.M. Tenbroek, M. S. L. Lee, W. Redman-White, R.J.T. Bunyan and M. J. Uren, “Self-heating effects in SOI MOSFET’s and their measurement by small signal conductance techniques,”IEEE Trans.Electron Devices, vol. 43, pp. 2240–2248,1998

[4] M. Pelgrom, A. Duinmaijer, and A. Welbers, “Matching properties of MOS transistors,” IEEE J. Solid-State Circuits, vol. 24, no. 5,

pp. 1433–1439, May 1989

[5] E.Malavasi, E.Charbon, E.Felt, and A.Sangiovanni-Vincentelli, “Automation of IC layout with analog constraints,” IEEE Trans. Computer-Aided Design, vol. 15, pp. 923–942.1996.

[6] A. G. Kokkas, 'Thermal analysis of multiple layer structures,”.

ZEEE Trans. Electron Devices, vol. ED-21, pp. 674-681,1974.

[7] G. Gao, M. Wang, X. Gui and H. Marcos, “Thermal Design Studies of

... Transactions on Electron Devices, vol. 36, pp 854-862, 1989

[8] C. Kim, N. Goto and K. Honjo, “Ultra-low-power and high-speed SiGe base bipolartransistors for wireless telecommunication systems“, IEEE Trans. Electron Devices, vol. 45, pp. 1287-1294, 1998

[9] N. Rinaldi, “Thermal analysis of solid-state devices and circuits: an analytical approach”, Solid-State Electronics,

vol. 44, pp. 1789-1798, 2000

[10] C Haji-Sheikh, “Peak temperature in high-power chips”,IEEE Trans.

Electron Devices, vol. ED-37,pp. 902-907,1990.

[11] J. Bastos, M. Steyaert, A. Pergoot, andW. Sansen, “Mismatch

characterization of submicron MOS transistors,” Analog Integrat. Circuits Signal Process., vol. 12, no. 2, pp. 95–106, Feb. 1997.

[12] A. L. Palisoc and C. C. Lee, “Thermal properties of the multilayer

infinite plate structure”, J. Appl. Phys., vol. 64, pp. 410-415, 1988.

[13] R. Joy and E. Schlig, “Thermal properties of very fast transistors”,

IEEE Trans. Electron Device, vol. 17, p. 586, 1970.

[14] L. Liou and B. Bayraktaroglu, “Thermal stability analysis of

AlGaAs/GaAs heterojunction bipolar transistors with

multiple emitter fingers”, IEEE Trans. Electron Devices, vol. 41, pp.

629-636, 1994.

[15] T.-H. Yeh, J. Lin, S.-C. Wong, H. Huang, and J. Sun, “Mis-match characterization of 1.8 V and 3.3 V devices in 0.18 _m mixed

International Journal of Scientific & Engineering Research, Volume 6, Issue 5, May-2015 221

ISSN 2229-5518

signal CMOS technology,”Proc. IEEE Int. Conf. Microelectronic Test

Structures,, pp. 77-82, 2001.

[16] D. Tjapkin and B. Radjenovic, “A delta model of nonstationary heat transfer in p-n junctions,” in Proc. ETRAN, pp. 102, 2002

[17] B. Radjenovic and D. Tjapkin, “An analytical model of the transient thermal behavior of semiconductor devices,”in Proc. BPU-5, pp. 649-

652, 2003

[18] P. Kinget and M. Steyaert, “Impact of transistor mismatch on the speed-accuracy-power tradeoff of analog CMOS circuits,” in Proc

.IEEE Custom Integrated Circuits Conf. (CICC), pp.333–336, 1999.

[19] J. Bastos, M. Steyaert, R. Roovers, P. Kinget, W. Sansen, B.Graindourze, N. Pergoot, and E. Janssens, Mismatch characterization of small size MOS transistors” in Proc. IEEE Int. Conf. Microelectronic Test Structures, pp. pp. 271–276, 1995

[20] J. Bastos, M. Steyaert, A. Pergoot, andW. Sansen, “Mismatch characterization of submicron MOS transistors,” Analog Integrat. Circuits Signal Process., vol. 12, no. 2, pp. 95–106, Feb. 1997.

[21] P. E. Bagnoli, C. Casarosa, M. Ciampi and E. Dallago“Thermal re-

sistance analysis by induced transient (TRAIT) method for power electronic,” ... IEEE Transactions on Power Electronics, vol. 13, no. 6, pp. 1208-1219, 1998

[22] C. C. Lee and A. L. Palisoc, “Real-time thermal design of integrated

...Trans. Comp., Hybrids, Manufact. Technol., vol. 11, pp. 485492,

1988.

[23] P. R. Gray, D. J. Hamilton, and J. D. Lieux, “Analysis and design of temperature stabilized substrate integrated circuits,” IEEE J. Solid State Circuits, vol. sc-9, 2, pp. 61-69, 1974