International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 1

ISSN 2229-5518

An Innovative Methods of Analysis and Applica- tions of Boolean Algebra in Boolean Matrices

Mrs.J.Evangeline Cicelia*, Dr.K.Ramanathan & Dr.K.Rangarajan*

Abstract— In this paper, we consider a new approach to Boolean Algebra in Boolean Matrices which entails the new method. Basically Boolean Algebra leads us to solve quadratic equation and cubic equation. After converting the equation into Boolean matrices it gives us the solution alter- natively by avoiding tedious calculation and lengthy process. This paper gives a solution with this new approach.

Index Terms— Boolean Algebra. Boolean Matrices. Quadratic. Cubic Equations. Binary representation.

1 INTRODUCTION

——————————  ——————————

imple Boolean Quantity: We define a simple Boolean quantity as that which is capable of assuming two values.

These values will be denoted by 1 and 0

Examples of Boolean quantities: (a) In logic a proposition can be true or false. The value of a proposition i.e. its truth or falseness is a Boolean quantity. We shall assign arbitrarily the values 1 to true and 0 to false. (b) In a computer, devices with two states are often encountered. e.g. a terminal can have a potential of 0 or 8 V only. The state of this terminal is a Boole- an quantity.

Order Relation: We can define a total order relation on the set of values of a simple Boolean variable simply by putting 0 < 1.

Tamil Nadu, India. E-mail : evangelinecicelia@gmail.com
The simple Boolean quantities which compare them will usu- ally be denoted by the corresponding small letter, with a sub- script recalling that it is a corresponding element of the sup- port set, e.g.,
x1, x2, x3,...... xn.
In practice we shall limit ourselves to the case when the sup- port set is finite and the components are written in the column form:

x 2

X = .

We also shall employ the symbols >, significance.

, 

with their usual

x n

We shall denote by 0 the general Boolean quantity all of whose components are zero, and by I the general Boolean quantity, all

Duality: We shall give this name to the application of the

mapping onto itself of the set of values of a simply Boolean variable, defined by 0  1, 1  0
If x is a simple Boolean quantity, we shall denote its dual by x*. It can be verified at once that (x*)* = x. Duality is a symmetric relation.
of whose components are 1. If desired, the simple Boolean quantities may be regarded as general Boolean quantities with one component.

Spatial representation of a general Boolean quantity: Let X

be a general Boolean quantity with n components. Each of the
If x1 > x2 then x *
in an inequality.

 x * i.e. duality reverses the order relation

components can take two values so that X has 2n distinct pos- sibilities. We consider in n-dimensional space the points
whose coordinate values are 0 or 1. To each possible X there

General Boolean quantity: Let E be a finite or infinite set that can be organized in any manner whatever:

Finite case: Column, Matrix.

Infinite case: Sequence of points Mn, Segment.
With each element of this set we associate a simple Boolean quantity. We thus obtain a general Boolean quantity. We de- note it as X.

* Professor, Department of Mathematics,

Bharath Institute of Science & Technology (BIST), Bharath University, Selaiyur, Chennai – 600073,

corresponds one and only one of these points. The points form the vertices of a hypercube.
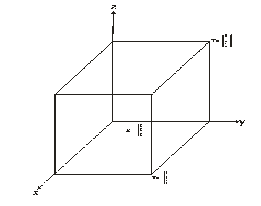
A segment for n = 1, a square for n = 2, a cube for n = 3. Fig. 1.1 depicts the case n = 3 in perspective.
We have indicated the value of X at certain of the vertices.
Representation of the hypercube presents difficulties for n  3, but it continues to offer a convenient geometrical lan- guage.
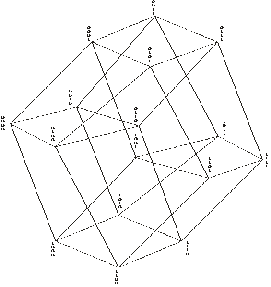
The representations for n = 4 may be seen in Figs. 1.2, 1.3, 1.4. In Fig. 1.2 the last component is 1 for the outer cube, 0 for the inner cube. The other components are located on each of the
cubes as in three-dimensional space.

International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 2

ISSN 2229-5518

The eight cubes forming the hypercube may easily be found in
Fig. 1.3.
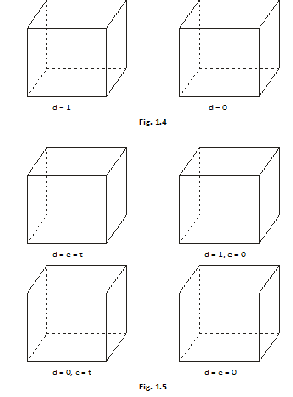
The representation of Fig. 1.4 may even be extended to five variables if desired, Fig. 1.5.

Binary representation of general Boolean quantities: Another convenient method of representing the 2n values of X consists in writing the components in a row, the 0’s and 1’s of which they are built up being regarded as binary digits. An integer lying between 0 and 2n-1 inclusive is thus associated with each value of X. This integer will be termed the affix of the vertex.

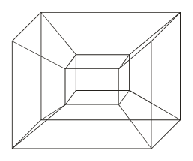
Fig. 1.1

Fig. 1.2

Fig. 1.3

In manuscript, it is convenient to write the affix as a decimal or octal number.

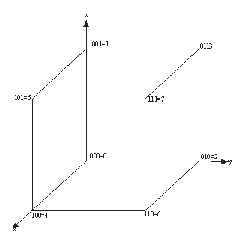
The Fig. 1.6 shows the correspondence, for n = 3 be- tween the vertices of the hypercube and the affixes in decimal form.

BOOLEAN MATRICES

Fig. 1.6

International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 3

ISSN 2229-5518

Definition (Boolean Matrix): By a Boolean Matrix of size mXn matrix over Bo. Let Bmn denote the set of all mXn such matrices. If m = n we write Bn. Elements of Bmn are often called relation matrices, Boolean relation matrices, binary relation matrices, binary Boolean matrices, (0, 1)– Boolean matrices and (0, 1) matrices.

Examples:

only if its dimension is atleast 7 or is 1.
Proof: Let M be a square root of J ɵ I of dimension less than
7. Then all diagonal entries of M are zero, and at least one of mij, mji is zero for each i, j. thus for each i the three sets {i}, {j:mi
= 1}, {j : mji = 1} are disjoint. So one of the latter two sets con- tains at most two elements. By possibly transposing M, as- sume that the third set has at most two elements.
If {j : mji = 1} = {a, b} then mai = 1 and mji = 0 for j ≠ a, b.

1

A = 1

0

1 0

0 

1 0

Moreover i ≠ a and i ≠ b since all diagonal entries are zero. Since M2 = J ɵ I we have Σmax.mxi = 1. But the only non-zero term of this sum is mab . mbi. Thus mab = 1. Also Σmax.mxi = 1. Its only non-zero term is mba . mab. Thus mab = mba = 1. But this
implies maa(2) = 1 which is false. Likewise the case {j : mji = 1} =
Definition (Row, Column of Matrix): Let A = (aij) Bmn. Then the element aij is called the (i, j) entry of A. The (i, j) entry of A is sometimes designated by Aij. The ith row of A is the sequence
{a} and is equal to ɵ are impossible, unless the dimension is 1.
For large values of n, there are circulants which are square roots of J ɵ I. if S is the set of l’s in the last row of a cur-
ai1, ai2,… ain and jth column of A is the sequence a1j, a2j,… amj. Let
culant M, M2
will be J ɵ I if and only if {a+b : a, b  S} includes
Ai* and A*i denote the ith row and ith column of A respectively.
In the above Example,
numbers in every congruence class modulo n except 0.
If n is odd and at least 9, S =

0

 n

1, 2,........ 

2, n ,

n 

 2 will do. If n = 7, S = 1, 2, 4 will

  

2 2 2 

A1* = [1 1 0] and A*3 = 0

0

do.
If n is even and atleast 12, let S =

 , 2,........n  3, n 1, n  2 . For n = 8, 10 we use a differ-

Definition: (Zero Matrix, Identity Matrix, Universal Matrix) 1

The n x m zero matrix 0 is the matrix all of whose entries are 

2 2 2 

zero. The n X n identity matrix I (δij) such that δij = 1 if i = j and δij = 0 if i ≠ j. The n x m universal matrix J is the matrix all of whose entries are 1.
Zero Matrix:
Identity Matrix
ent construction.

0 1 0 o

 

1 0

0 0 1 

0

A = 0

0

0 0

0 

0 0

1 0 0

 

where the top and bottom diagonal blocks are 1 x 1, the edge blocks are entirely 1 or entirely 0 as indicated, and the inner four blocks are circulants. For both 8, 10 we can solve to find appropriate circulants.
For n = 7, M is unique up to conjugation by a permu-
tation. However this is not so far large n. This completes the
A = 0 1

0 0

0

1

proof. For more details about the square root of J ɵ I see
Raghavan [5].
Universal Matrix

Example: When n is even and atleast 12,

1

A = 1

1

1 1

1 

1 1

Let S = {1, 2, 3, 5, 8}.

Note: Every identity matrix is Boolean Matrix. But it is not suitable for zero and Universal Matrices.

QUADRATIC EQUATIONS

Theorem: The Boolean matrix J ɵ I has a square root if and

International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 4

ISSN 2229-5518

0

0

0 0 1

Q12 = 



0 0 0

1 0 0



0 1 0

0 0 1



1 0 0

0 1 0



1 0 1



1 1 0

1 1 1

1 1 0 1

1 1 1 0

0 1 1 1

0 0 1 1

0 0 0 1

0 0 0 0

1 0 0 0

0 1 0 0

0 0 1 0

1 0 0 1

0 1 0 0

0 0 1

1 0 0

0 1 0

1 0 1

1 1 0

1 1 1

0 1 1

0 0 1

0 0 0

1 0 0



1 0



0 

0 0



1 0

0 1



1 0

1 1



1 1



0 

0 0

Q12 X Q12 = (J - I)12

0

1



1



1



1



1



1

1

1 1 1

0 1 1

1 0 1

1 1 0

1 1 1

0 1 1

1 0 1

1 1 0

1 1 1

0 1 1

1 0 1

1 1 0

1 1 1

1 1

1 

1 1



1 

1 1



1 1



1 1



1 1



0 

1 0

Q33 x Q33 =

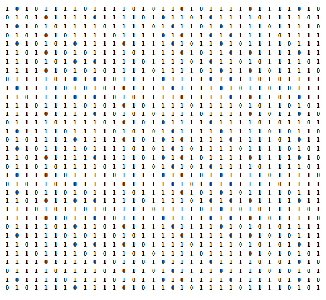
and hence the theorem.

CUBIC EQUATIONS

Theorem: The Boolean matrix J ɵ I has a cube root which is symmetric circulant whenever its dimension is at least 30.

Proof: Let n denote the dimension.

If n = k (mod 5,0, k = 0, 1, 3 take the circulant whose last row has ones in locations congruent to + 1, +(5a + 3) for all non-

negative integers a such that 5a + 3 < .

If n = 10x + 17, take the circulant whose row has ones in locations 1, 3, 8, ….., 3+5(x-1), 3+5x, 5+5x, 105x, n-(10+5x),….

B33 = Q33 x Q33 x Q33 = (J - I)33
Hence the theorem.

ACKNOWLEDGMENT

The authors are thankful to the Management for the financial assistances.

REFERENCES

(n-1), where x is the largest integer such that 3+5x <
proves the theorem.

Example: K = 3 n = 33 (mod 5)

Q33 =

. This

[1] Elliott Mendelson, “Boolean Algebra”, Schaum’s Outline Series,

1970.

[2] Haskell B.Curry, “Foundations of Mathematical Logic”, Dover Pub- lications, Inc., New York, 1976.

[3] Ki Hang Kim, “Boolean Matrix Theory and Applications”, Marcel

Dekker, Inc., New York and Basel, 1982.

[4] Kunizmann J, “Fundamental Boolean Algebra”, Translated by SCRIPTA TECHNICA LTD., Edited by B. GIRLING, Blackie and Son Limited, London and Glasgow, 1967

[5] Raghavan K, “Squareroot of a Boolean Matrix J-I”, Journal of Indian

Institute of Science, Bangalore, India, 1991.

International Journal of Scientific & Engineering Research Volume 4, Issue3, March-2013 5

ISSN 2229-5518

IJSER lb)2013

http://www.ijserorq