International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 1342
ISSN 2229-5518
M.A.K.Azad, L.S. Andallah
1
ut + uu x + Px =
![]()
u xx for -P x =e
Re
using Orlowski and Sobczyk transformation (OST). The effect of pressure gradient and
Reynolds number for different cases are studied.
Key-words- Burgers equation, Cole-Hopf transformation, Diffusion equation, Orlowski and Sobczyk transformation (OST),
Pressure gradient, Reynolds number, 1D NSE.
1 INTRODUCTION
—————————— ——————————
The Navier-Stokes equation is an important governing equation in fluid dynamics which describes the motion of fluid.
The exact solution for the NSE can be obtained is of particular cases. The Navier-Stokes equation is non-linear; there can not be a general method to solve analytically the full equations. It still remains one of the open problems in the mathematical physics. Exact solutions on the other hand are very important for many reasons. They provide a reference solution to verify the accuracies of many approximate methods.
In order to understand the non-linear phenomenon of NSE, one needs to study 1D NSE. Due to the fact that it posses both the
diffusion and advection terms of the NSE, it embodies all the
main mathematical features of the NSE.
Applying OST we have reduced 1D NSE to viscous Burgers
equation and we have solved viscous Burgers equation
T. Yang and J.M. McDonough [6] presented exact solution to a
one-dimensional Burgers’ equation which exhibits erratic turbulent-like behavior. They compared time series of the exact solution with physical experimental data. He also mentioned the governing equation is analogous to 1D Navier-Stokes equation. They also proposed a model to provide a good tool for testing numerical algorithms. J Qian [7] presented numerical experiments on one dimensional model turbulence.
In this paper, we present the analytical solution of 1D NSE. We
compare the solution of 1D NSE including and excluding pressure gradient. We also analyze the pressure gradient and Reynolds number effect in the solution.
Using the dimensionless definitions,
analytically by using Cole-Hopf transformation. So a number of analytical and numerical studies on 1D NSE and 1D viscous Burgers equation have been conducted to solve the governing![]()
x = x , u =
L
![]()
u , p =
V
p *
![]()
ρV 2
, t =
t *V
![]()
L
equation analytically [1],[2],[3],[4],[5],[6],[7]. www.coolissues.com/mathematics/NS [1] studied on analytic
we consider the1D NSE in non-dimension form [1],[6] as
solution of 1D NSE including and excluding pressure term. Neijib
Smaoui [2] studied numerically the long-time dynamics of a system of reaction-diffusion equation that arise from the viscous
ut +
uux
+ Px
![]()
= 1 u
Re xx
(1)
where
Burgers equation which is 1D NSE without pressure gradient. Hans J. Wospakrik* and Freddy P. Zen+ [3] presented the solution of the initial value problem of the corresponding linear heat type equation using the Feymann-Kac path integral formulation. A. Orlowski and K. Soczyk [4] presented a transformation to make
x ∈ (a, b), t ∈ (to , t f ) .
With u(x,t) denotes velocity, subscripts denote partial differentiation. We consider pressure gradient as an exponentially
inhomogeneous Burgers equation to homogeneous form. Ronobir C. Sarker, L.S. Andallah and J. Akhter [5] studied on analytic solution of viscous Burgers equation as an IVP. Due to the
decreasing function of t of the form -
As a result “ (1)” can be reads as
Px = f
(t )
= e− at −b .
complexity of the analytical solution they studies explicit and
implicit finite difference schemes for viscous Burgers equation and determined stability condition for both schemes.
ut + uu x
1
− cu xx
υ
= f (t)
(2)
where f (t ) = e− at −b
and
—————————— ——————————
Muhammad Abul Kalam Azad, Ph. D student, Department of Mathematics, Jahangirnagar
University,Savar,Dhaka,Bangladesh, Email:akazad2034@gmail.com
Professor Dr.. Laek Sazzad Andallah, Department of Mathematics, Jahangirnagar University, Savar,Dhaka,Bangladesh,Email:andallahls@gmail.com
![]()
![]()
c = = .
Re VL
In order to determine analytical solution of “(2)” first we reduce the equation to Burgers equation by using OST in[4]. Then
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 1343
ISSN 2229-5518
solving Burgers equation analytically we obtain the analytical
solution of 1D NSE “(2)” by using inverse OST . The OST is defined as
We perform the transformation in three steps.
u' = φx
First let us assume .
x' = x − φ (t), t' = t, u' ( x', t' ) = u( x, t) − W (t)
(3)
With this transformation “(8)” becomes
WithW (t ) = ∫
t t
f (τ )dτ ,φ (t ) = ∫ W (τ )dτ
(4)
φt '
1 2 ![]()
φ x '
2
= (cφ x 'x ' )x '
0 0
x '
t
W t = f τ dτ
0
![]()
= 1 (e −b − e −at −b ) .
a
Now integrating the transformed equation w.r.t. x´, then we have
t 1
e − at −b
e −b 1 2
Again φ (t ) = W (τ )dτ =
0
![]()
![]()
![]()
![]()
te −b + −
a a a
φt ' + φx '
2
= cφx 'x '
![]()
![]()
![]()
Thus we get x ' = x − 1 te −b − 1 e −at −b + 1 e −b
(5)
Then we make the transformation
t ' = t
a a 2 a 2
(6)
φ = −2c lnψ
![]()
u' (x' , t ') = u( x, t ) − 1 e −b +
a
![]()
1 e −at −b .
a
(7)
φt '
![]()
= −2c ψ t '
ψ
∂u =
u' .
1 e−b
1 e−at −b + ∂u' + e−at −b . ψ
![]()
![]()
![]()
![]()
![]()
= ∂ − +
φ = 2c x '
![]()
∂t ∂x' a
a ∂t '
x ' ψ
![]()
![]()
∂u = ∂u' .
φ ' ' = −2c
![]()
ψψ ' ' −ψ ψ'
ψ
' = −2c
![]()
ψψ ' ' −ψ '
ψ
∂x ∂x'
x x x x
x x 2
x x x
2
Also![]()
![]()
∂ u = ∂
u' .
Substituting these derivatives in (11) , we obtain
∂x 2
∂x'2
ψ t ' = cψ x ' x '
Substituting these transformed derivatives in “ (2)” , we get
∂u' ∂u' ∂ 2 u'![]()
![]()
![]()
+ u' = c .
Which is the well-known first order PDE called heat or diffusion equation in [10],[11].
∂t '
⇒![]()
∂u'
∂x'![]()
+ u' ∂u'
∂x' 2![]()
= 1
∂ 2 u'
(8)
From “ (10)” we get
∂t '
∂x'![]()
c = 1
Re ∂x' 2![]()
= υ .
ψ (x' , t ') = Ce
![]()
− 1 u ' x 'dx '
2c
(13)
Where
Re VL
For t´=0, “(13)” gives
Again, we know that the non-dimension form of Burgers equation![]()
− 1
ψ (x',0) = e 2c
u (z )dz = ψ
(x')(let )
∫0 o 0
is![]()
∂u *![]()
![]()
+ u * ∂u = 1
∂ 2 u *
(9)
After C-H transformation our problem turns into the following
∂t *
∂x *
Re ∂x * 2
Cauchy problem for the heat equation in [5],[10],[11],[12]
So, “ (8)” is the transformed 1D NSE after applying OST and it is
ψ t ' = cψ x ' x ' ,ψ (x',0) = ψ
![]()
− 1 x '
= e 2c ∫ u
′ (z )dz
(14)
analogous to non-dimension form of Burgers equation “ (9)”.
Now we need to solve “(8)” with initial condition
0 0 0
This is a pure initial value problem and for solving this problem,
u(x′,0) = u 0 (x′,0)
for
− ∞ < x' < ∞.
we get![]()
= 1 ∞
(x'− y )2
−
− =1 y ′
(15)
“(8)”can be linearized by the Cole-Hopf transformation in [8]
φ x
ψ (x' , t ')
4πkt ' ∫−∞ exp
4ct '
2c ∫0 u0 ( z)dz dy
![]()
u' ( x' , t ' ) = −2c .
φ
Differentiating “(15)” w.r.t. x´, we obtain
(10)
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 1344
ISSN 2229-5518
= 1 × − 1 ∫∞ (x'− y )exp− (x'− y )
![]()
− 1 ∫ y u ′ ( z)dz dy (16)
∞ (x'− y )2
∫ x'− y exp −
![]()
+ 1 cos ydy![]()
![]()
ψ x '
4πkt '
2ct ' − ∞
4ct'
2c 0 0
−∞
![]()
u' (x', t ') =
4ct' 2c
(19)
∞ (x'− y )2 1
Now from “ (10)” we get
t ' ∫−∞ exp−
![]()
4ct'![]()
+ cos ydy
2c
∫ (x − y )
(x'− y )2
−
− 1 ∫ y u ′ ( z)dz dy
(17)
' exp
−∞ 0
(17)
u (x
![]()
) = ct c
' ', t '
4 '
∞ (x'− y )2 1
![]()
t − −
2
y ′
u ( z)dz dy
For x´=0, “ (19)” becomes
( y )2 1
' ∫−∞ exp
4ct'
2c ∫0 0
∫−∞ (−
y )exp− −
![]()
+ cos
ydy
(20)
Now by applying inverse OST, we have
u' (0, t ') =
4ct' 2c
∞ (− y )2 1
u(x, t ) = 1 e −b − 1 e − at −b
t ' ∫−∞ exp−
![]()
4ct'![]()
+ cos ydy
2c
a a
x − 1 te −b − 1 e − at −b + 1 e −b − y
The numerator of “(20)” is an odd function, so we must have
2
∞ 2 2
∫ x − te −b − e − at −b + e −b − y exp− − ∫ u (z )dz dy
−∞ a a 2
a 2
4ct
2υ 0 0
u´(0,t´)=0.
+ (18)
x − 1 te −b − 1 e − at −b + 1 e −b − y
t ∫∞ exp− a a a − 1 ∫ y u (z )dz dy
Now for x´=2π, “ (20)” becomes
−∞
2 2
4ct
2c 0 0
∞ ( )
(2π − y )2 1
This is the analytical solution of 1D NSE. Here it is very
∫−∞ 2π − y exp−
4ct'
![]()
+ cos ydy
2c
(21)
u' (2π , t ') =
important that for very small t, both numerator and denominator
∞ (2π − y )2
t ' ∫ exp−
![]()
+ 1 cos ydy
of “ (18)” get very closed to zero and thus very difficult to handle
−∞
4ct' 2c
numerically. Again, for very small c, both numerator and
Making the variable change z=2π-y, we get
∞ z 2 1
denominator of “(18)” get very closed to zero or infinity which![]()
![]()
∫−∞ z exp− 4ct' + 2c cos z dz u' 2π , t ' =
2
(22)
∞ z
![]()
t ' exp
![]()
1 cos
becomes very difficult to handle.
3 UNIQUENESS OF THE SOLUTION
∫−∞
− 4ct' + 2c
zdz
The function under integration sign in the numerator is an odd
Now one question may arise whether our solution is unique or
not. The OST of 1D NSE reduces to Burgers equation.Then the
function, so we can take
∞ z 2 1
![]()
∫ z exp− ct
![]()
+ cos z dz = 0.
c
Cole-Hopf transformation reduces it to heat equation. Widders
uniqueness theorem in [ 10],[11] ensure the uniqueness of heat equation in 1D case. Thus we can say that the analytical solution
−∞ 4 ' 2
Thus we get u´(2π,t´)=0.
Hence for 1D NSE without pressure term we get the boundary
“(18)” is unique.
4 BOUNDARY VALUES OF THE SOLUTION
At first we find the values of the analytical solution “(11)” with
values
u′(0, t′) = 0
u′(2π , t′) = 0
(23) (24)
initial u0(x´)=sinx´ at the boundaries of the spatial domain [0,2π] which in further will be used as boundary conditions for numerical scheme.
For initial condition u 0 (x´)=sinx´ ,we get the analytical solution
and initial condition is u´(x´,o) = sinx´ (25) Now, our aim to find out u(x,0),u(0,t),u(2π,t).
From relation (7), we have![]()
![]()
u(x, t ) = u' (x' , t ') + 1 e −b − 1 e −at −b
a a
“(17)” as
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 1345
ISSN 2229-5518
![]()
![]()
∴ u(x,0) = u' (x',0) + 1 e −b − 1 e −a.0−b
a a
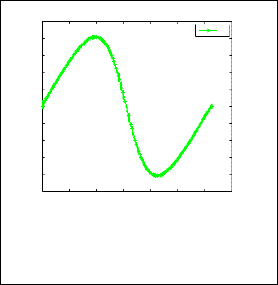
1D Navier-Stokes equation taking m = 150,n = 1500, c = 0.2
![]()
![]()
= u' (x',0) + 1 e −b − 1 e −b
0.25
t=6
a a 0.2
0.15
= sinx´ ;[from “(25)”]
= sinx ;[from “(5)”]
0.1
0.05
From “ (23)”, we have![]()
u' (x' , t ') = u( x, t ) − 1 e −b +
a
![]()
1 e −at −b .
a
0
-0.05
-0.1
-0.15
![]()
![]()
⇒ u' (0, t ') = u( x, t ) − 1 e −b + 1 e −at −b ; [∀x′ = 0].
-0.2
a a -0.25
0 1 2 3 4 5 6 7
Spatial co-ordinate (x)→
![]()
![]()
⇒ 0 = u( x, t ) − 1 e−b + 1 e− at −b ; [ from" (5)"]
a a
Fig.1. Analytical solution of 1D NSE dropping pressure
e −b + 1 e
⇒ u( x, t ) = 1 e −b − 1 e −at −b
![]()
gradient. 2
![]()
![]()
a a a
Since R.H.S of “(26)” is independent of x , so we can write![]()
![]()
u(0, t ) = 1 e −b − 1 e −at −b .
a a
![]()
![]()
u(2π , t ) = 1 e −b − 1 e − at −b
(26)
for
a
![]()
x = 1 e −b +
a
a
![]()
![]()
1 e − at −b − 1
a 2 a 2
e −b .
1.85
1.8
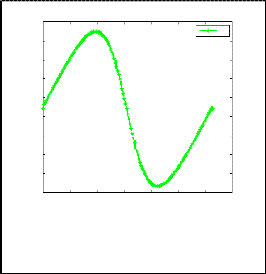
1D Navier-Stokes equation taking m = 150,n = 1500,a = 0.6,b = 0, c = 0.2 t=6
Thus we get the initial and boundary condition of 1D NSE “(1)”
as follows:
1.75
1.7
1.65
u(x,0) = sin x −
![]()
1 te −b −
a
![]()
1 e −at −b +
a 2
![]()
1 e −b
a 2 .
1.6
1.55
1.5
![]()
![]()
u(0, t ) = 1 e −b − 1 e −at −b
![]()
![]()
u(2π , t ) = 1 e −b − 1 e −at −b .
1.45
a a , a a
1.4
0 1 2 3 4 5 6 7
Spatial co-ordinate (x)→
5.1 PRESSURE GRADIENT EFFECT ANALYSIS
Fig. 2. Analytical solution of 1D NSE.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 1346
ISSN 2229-5518
1.65
1.6
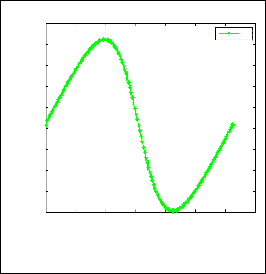
1D Navier-Stokes equation taking m = 150,n = 1500,a = 0.7,b = 0, c = 0.2
t=6
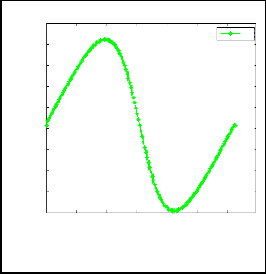
1D Navier-Stokes equation taking m = 150,n = 1500,a = 0.5,b = 0.3, c = 0.2
1.65
1.55
1.6
t=6
1.5
1.55
1.45
1.5
1.4
1.45
1.35
1.4
1.3
1.35
1.25
1.3
0 1 2 3 4 5 6
Spatial co-ordinate (x)→
Fig. 3. Analytical solution of 1D NSE.
1.25
0 1 2 3 4 5 6
Spatial co-ordinate (x)→
Fig. 5. Analytical solution of 1D NSE.
1.45
1.4
1D Navier-Stokes equation taking m = 150,n = 1500,a = 0.8,b = 0, c = 0.2 t=6
1D Navier-Stokes equation taking m = 150,n = 1500,a = 0.5,b = 0.4, c = 0.2
1.5
t=6
1.45
1.4
1.35
1.3
1.25
1.2
1.15
1.1
1.35
1.3
1.25
1.2
1.15
1.05
1
0 1 2 3 4 5 6 7
Spatial co-ordinate (x)→
1.1
1.05
0 1 2 3 4 5 6
Spatial co-ordinate (x)→
Fig. 4. Analytical solution of 1D NSE.
Fig. 6. Analytical solution of 1D NSE.
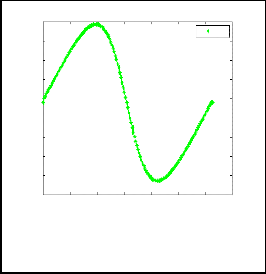
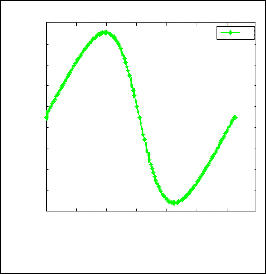
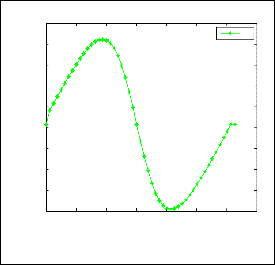
From fig. 2, fig.3, fig.4 we observe that keeping b = 0 and increasing the value of a , pressure gradient is decreasing continuously and at t = 6 in each case velocity is decreasing. Since P x is negative pressure gradient decreases in the direction of flow and the pressure gradient is favorable. Here pressure gradient is directly proportional to velocity.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 1347
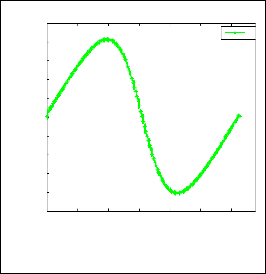
ISSN 2229-5518
1D Navier-Stokes equation taking m = 150,n = 1500,a = 0.5,b = 0.5, c = 0
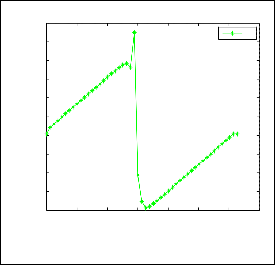
1.4
1.35
1.3
1.25
1.2
1.15
1.1
1.05
1
0.95
0.9
0 1 2 3 4 5 6
Spatial co-ordinate (x)→
t=6
1D Navier-Stokes equation taking m = 50,n = 150,a = 0.5,b = 0.3, c = 0.04
2
t=6
1.9
1.8
1.7
1.6
1.5
1.4
1.3
1.2
1.1
1
Fig. 7. Analytical solution of 1D NSE.
0 1 2 3 4 5 6 7
Spatial co-ordinate (x)→
Fig.9. Analytical solution of 1D NSE taking Re = 25.
Comparing above figures we conclude that pressure term has an important effect on the solution of 1D NSE. From the above fig.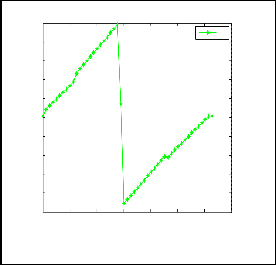
5, fig.6, fig.7 we observe that an increase in the pressure gradient
resulted an increase in the velocity of the fluid. Also a decrease in
1D Navier-Stokes equation taking m = 50,n = 150,a = 0.5,b = 0.3, c = 0.008
1.9
the pressure gradient resulted a decrease in the velocity of the fluid which describes a phenomenon in which the pressure of a fluid changes with a change in the velocity of the fluid.
5.2 REYNOLDS NUMBER EFFECT ANALYSIS
1.8
1.7
1.6
1.5
1.4
t=6
1.3
1.65
1.6
1D Navier-Stokes equation taking m = 50,n = 150,a = 0.5,b = 0.3, c = 0.2 t=6
1.2
1.1
1
1.55
1.5
0.9
0 1 2 3 4 5 6 7
Spatial co-ordinate (x)→
1.45
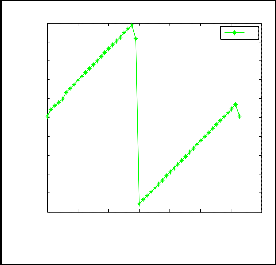
Fig.10. Analytical solution of 1D NSE taking Re =125
1.4
1.35
1.3
1.25
0 1 2 3 4 5 6 7
Spatial co-ordinate (x)→
1D Navier-Stokes equation taking m = 50,n = 150,a = 0.5,b = 0.3, c = 0.002
1.9
t=6
1.8
1.7
1.6
1.5
Fig.8. Analytical solution of 1D NSE taking Re = 5.
1.4
1.3
1.2
1.1
1
0.9
0 1 2 3 4 5 6 7
Spatial co-ordinate (x)→
IJSER © 2014 http://www.ijser.org
Figure-11: Analytical solution of 1D NSE taking Re = 500.
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 1348
ISSN 2229-5518
From fig.7, fig.8, fig.9, fig.10, fig.11 we observe that our initial date is smooth and c is very small i.e. Reynolds number is very large, then before the wave begins to break and shock forms. In the limit, as c tends to zero, the solutions to the 1D NSE tend to shock wave solutions. From these figures we also observe that for the first loop when the c tends to larger then the velocity tends to smaller and when the c tends to smaller then the velocity tends to larger and for the second loop when c tends to larger the velocity tends to larger.
6 CONCLUSION
In this paper, we have presented analytical solution of 1D NSE taking –Px = e-at-b .Using the computational results obtained by implementing computer program we have found important impact of pressure gradient term on the solution of 1D NSE which is analogous to the phenomenon of nature. Reynolds number also plays a vital role on the solution of 1D NSE which may be stated as when Reynolds number is low then we get smooth solution. But when Reynolds number is large then shock forms.
REFERENCES
[1] Navier-Stokes type equations and their explicit solution. www.coolissues.com/mahematics/NS
[2] Neijib Smaoui, “Analyzing the dynamics of the forced
Burgers equation.”
[3] Hans J. Wospakrik* and Freddy P. Zen+ , “ Inhomogeneous Burgers equation and the Feymann-Kac path integral.”9812014v1,1998.
[4] A. Orlowski and K. Soczyk, Rep. Math. Phys. 27(1989) 59,
[5] Ronobir C. Sarker, L.S. Andallah and J. Akhter, “ Finite difference scheme for Burgers equation.” J.J Math and Math Sci.,Vol 26,2011,15-28.
[6] T. Yang and J.M. McDonough, “ Exact solution to Burgers
equation exhibiting erratic turbulent –like behavior.” aiaa04.pdf. [7] J Qian, “ Numerical experiments on dimensional model turbulence.”Phys. Fluids 27, 19571965,1984.
[8] D.T. Jeng and W.C. Meecham, “Solution of forced Burgers’
equation,” Phys. Fluids 15, 504-506, 1972.
[9] E. Hopf:Commun. Pure Appl. Math. 3,201-212(1950) J.D. Cole : Q. Appl. Math. 9,225-232(1951).
[10] D.V .Widder, “ The heat equation,” Academi Press,1975.
[11] D.V. Widder, “Positive temperature on an infinite rod,” Trans. Amer. Math,Sec.55(1944) 85-86.
[12] Md. Abdul Awal Sheikh, “ Analytical and numerical solution of Burgers’ Equation”, M. Phil thesis,Session:2008-2009.
[13] L.S. Andallah, “Analytical & Numerical methods for PDE” , Lecture notes, Department of Mathematics,Jahangirnagar University.
Savar,Dhaka.
IJSER © 2014 http://www.ijser.org