International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 1
ISSN 2229-5518
Abstract - In many industrial environments, systems are required to perform a sequence of operations (or missions) with finite breaks between each operation. During these breaks, it may be advantageous to perform repair and replace on some of the system’s components. Howe ver, it may not be possible to perform all desirable maintenance activities prior to the beginning of the next mission due to limitations on maintenance resources. In this paper we have used the selective maintenance policy for determining the optimum number of repairable and replaceable components to maximize the system’s reliability within limited maintenance time and cost. Also we find the optimal maintenance cost and optimal maintenance time for predetermined reliability requirement of the system. A numerical example is presented to illustrate the computational proc edure.
----------------------------------------*---------------------------------------------
The reliability in a broader sense has been defined as follows: reliability indicates the probability implementing specific performance or function of products and achieving successfully the objectives within a time schedule under a certain environment, W ang, Z.H. (1992). In general, a higher priority is placed on quality control rather than reliability in the process of manufacturing. Nonetheless, high quality is not equivalent to high reliability. For example, a certain component, which has passed quality control procedure in conformity to the specifications, may lead to problems when operating with other components. This involves reliability design that is related to electrical or mechanical interface compatibility among spare parts. W ith the rapid technological progress and increasing complexity of s ystem structure, any failure of any component may lead to system malfunction or serious damage. For instance, a weapon system is a precise and sophisticated system that comprises several sub-systems, components and spare parts. Failure of even a single element will likely have adverse impact upon the operability of the weapon system, and thus may become threat to the national security.
A repairable system is a system that can be repaired to operate normally in the event of any failure such as computer network, manufacturing system, power plant or fire prevention system. Availability comprises “reliability” and “recovery part of unreliability after repair”, indicating the probability that repairable systems, machines or components maintain the function at a specific moment”, W ang, Z.H. (1992). It is generally expressed as the operable time over total time.
In recent years, reliability and availability have expanded their influence in various industries and fields, thus serve as an integral
A Series-parallel system indicates sub-systems in which several components are connected in parallel, and then in series, or sub- systems where several components are connected in series, and then in parallel. A series-parallel system can be improved by four methods, W ang, Z.H. (1992): (1) use more reliable components; (2) increase redundant components in parallel; (3) utilize both #1 and #2; and (4) enable repeatedly the allocation of entire system framework. For the framework of series-parallel system, it is very difficult to find out an optimal solution under multiple constraint conditions Chern, M.S. (1992). Painton and Campbell (1995) solved the reliability optimization problem related to personal computer design. They regarded a personal computer as a series-parallel system of several components, each of which has three optional packages.
The selective maintenance operation is an optimal decision-making activity for systems consisting of several equipments under limited maintenance duration. The main objective of the selective maintenance operation is to select the most important equipment or subsystem to maintain. It also has to determine the appropriate maintenance actions in order to minimize the sum of production losses due to the system failures and the maintenance cost during the next working time. Such kind of problems can be encountered for equipments that perform sequences of tasks and can be repaired only during intervals of tasks. Such cases occur in military equipment production lines in which maintenance actions are carried out on weekends, vehicles are maintained between two deliveries and computer systems are maintained at night, etc.
Rice et al. (1998) were the first to deal with the selective maintenance problem. They modeled a maintenance decision-making problem for a special type of series–parallel system, considering M subsystems in
quality element in the organization system and manufacturing process. To maintain the reliability of sophisticated systems to a higher level,
series, the
i th
subsystem consisting of
Ni , i
![]()
1,2,..., M
identical
the system’s structural design or system components of higher reliability shall be required, or both of them are performed simultaneously, Henley et al. (1985). The system structure is virtually designed under the limitations such as weight, volume or other technologies, so the reliability cannot be further improved. In this case, replacing highly reliable components can improve the system reliability. While improving the reliability of systems and components, the associated cost also increases. Thus, it is a very important topic for decision-makers to fully consider both, the actual business and the quality requirements.
parallel components. They considered constant fault rate for each
component, i.e. they assumed an exponential distribution for the component life, and considered only single maintenance mode. Cassady et al. (2001) , (2001) improved upon the Rice et al. (1998)
model by assuming W eibull distribution for component life and considered multiple maintenance modes, including minimal repair (MR) and replacement of faulted components, and preventive maintenance (PM) for the functioning component. Lust et al. (2009) also proposed a variant model. They set up a selective maintenance optimal model for the general series–parallel system containing multiple components, to maximize system reliability after the maintenance action, and
IJSER © 2012 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 2
ISSN 2229-5518
presented a solution algorithm by integrating the heuristic method with tabu search (TS).
One of the common grounds of the above models is that maximum
subsystem i all in the functioning state at the start of the mission. Since group X of the system is a series arrangement of the subsystems, its reliability can be defined as![]()
![]()
s
system reliability is the unique objective, which is undoubtedly meaningful for maintenance actions of security products, such as
R1 1 (1
i 1
![]()
ri )ni
![]()
, i 1,2,..., s
(2.1)
weapon equipments, airplanes, and spacecrafts. However, as for the
Similarly for group Y composed of (m![]()
s) independent subsystems
general manufacturing system, the economic factor cannot be neglected. Therefore, a balance between the fault loss reduction and the maintenance cost is needed as the ultimate objective of system
reliability improvement is also to minimize cost. Therefore, Cheng et al.![]()
( s 1 , s
as![]()
m
![]()
2 , … , m ) connected in series, the reliability can be defined![]()
![]()
![]()
n
(1999), took maintenance cost into account and set up a selective maintenance decision-making model for the multi-state system,
R2 1 (1
i s 1
ri ) i , i
s 1,..., m
(2.2)
although it is somewhat simple since the cost of the manufacturing system is more complex.
Since the system is a series arrangement of these two groups X and Y,
the complete system reliability can be defined by![]()
2
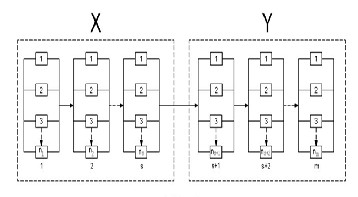
In this paper we assume that the system comprises two types of subsystems. One is the type of subsystems in which the components
R Ri ,
i 1
![]()
i 1,2
(2.3)
are very sensitive to the functioning of the whole system and,
therefore, on deterioration these should be replaced by new ones. Let these subsystems range from 1 to s . The other type of subsystems![]()
are those in which the components after deterioration can be repaired
W e will use the following notations in our formulation of the problem:
k i = Total number of failed components in the subsystem i at the end of a mission
and then replaced. Let such subsystems range from s
1 to m . In
p i = Number of failed components to be replaced or repaired in
fig. 1 the group X consists of the s subsystems with sensitive![]()
components which on failure are replaced by new ones and Y the
subsystem i prior to the next mission![]()
p ( p1,..., pm )
remaining (m
repaired.
s) subsystems in which the components can be
a i = Number of new components available for replacement in i th
subsystem of group X; i![]()
1,2,..., s
ti =Time units required for repairing and then replacing a failed
th
![]()
component in the i subsystem of group Y; i
s 1,..., m
T0 =Total time available for repairing / replacing the failed components in the system between two missions
' =Cost units required for replacing a failed component by a new one in the subsystem i (of group X)
"
ci = Cost units required for replacing a failed component after repairs
in the subsystem i (of group Y)
C 0 =Total cost available for repairing / replacing the failed components in the system
Subsystems.
Every industrial and engineering organization depends upon the effective performance of repairable and replaceable components of the system. A repairable component of a system can be defined as a component which after deterioration can be restored to an operating condition by some maintenance action. On the other hand a replaceable component is the one which after failure is replaced by a
new one.
Ideally, all the failed components in each subsystem of group X are replaced by new ones prior to the beginning of the next mission/ run. In a similar way, ideally all the failed components in the subsystems of group Y are repaired and then replaced prior to the beginning of the next mission/run. However, due to the constraints on the cost and time it may not be possible to repair and replace all the failed components in the system.
The time required for repairing and then replacing all the failed
components in i th subsystem of group Y is given by
W e consider a system which requires to perform a sequence of
ti ki , i
![]()
s 1,..., m
(3.1)
identical missions after every given (fixed) period. The system consists of several subsystems where each subsystem can work properly if at least one of its components is operational. Thus we are working under the following two assumptions
The maintenance time available for repairing and then replacing the
failed components between two missions is T0 time units.
Let us assume here that there is a s eparate server/ team for the repairs of the failed components in the subsystems of group Y. If
independent.![]()
T0 ti ki for at least one i, i
![]()
s 1,..., m then all the failed components
can not be repaired and replaced prior to the beginning of the next mission.
Let
ri denote the probability that a component of a subsystem i
Further, the cost required for replacing the failed components by new
ones in group X is
survives the mission given that the component is functioning at the![]()
s
C c ' k
(3.2)
start of the mission, and let
n denote the number of components in 1 i i
i 1
IJSER © 2012
International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 3
ISSN 2229-5518
and the cost required for replacing the failed components after repairs in group Y is![]()
m
![]()
![]()
![]()

![]()
s m
Min C '' ''
C2 i i i s 1
(3.3)
i 1 i s 1
![]()
![]()
s
Therefore, the total cost required to repair and/or replace all the failed components in the system prior to the next mission by adding (3.2) and
Subject to
1 (1
i ' 1
r ) ni
ki pi R *
![]()
(3.3) is obtained as C = C1 C2
Suppose that the total maintenance cost available for repairing and
t i pi
T0 , i
s 1,...., m
(4.6)
replacing of failed components between two missions is C 0 cost units.
0 pi
ai and int egers , i
![]()
1,...., s
If C 0![]()
C then also all the failed components can not be repaired
and 0 ![]() pi
pi
![]()
k i and int egers , i
![]()
![]()
s 1,...., m
and/or replaced prior to the beginning of next mission. In such cases, a method is needed to decide which failed components should be repaired and replaced prior to the next mission and the rest be left in a failed condition. This process is referred to as Selective Maintenance.
In the selective maintenance the number of components available for
the next mission in the i th subsystem will be
(ni
![]()
ki )
![]()
pi , i
![]()
1, 2,..., m . (3.4)
maintenance time for pre-determined reliability requirement R*
and
Now we discuss three mathematical programming models in different prospects for the decision-makers.
the given cost C0 . For this situation we assume that there is a single team for the repairs of the components of various subsystems of group Y. This means that the repairing of the components in the various subsystems of group Y is in series. Then the problem can be formulated as![]()

m
time between two missions. From (2.3) and (3.4), the reliability of the
system to be maximised is given by![]()
![]()
![]()
m
Min T
ti pi i s 1
![]()
![]()
![]()
s
R 1 (1
i 1
![]()
ri ) ni ki pi
(4.1)
Subject to
1 (1
i ' 1
![]()
r ) ni
ki pi R *
Since the total cost of replacing the components should not
exceed C 0 , we have
s
C t ' p
![]()
m
c '' p
(4.7)
![]()
s
c ' pi
![]()
m
![]()
c" pi C0
(4.2)
i 1
0 pi
i s 1
ai and int egers , i
![]()
1,...., s
i 1 i s 1
0 pi
k i and int egers , i
s 1,...., m
The maximum tolerable time between two missions (Spent in the repairs of the components in various subsystems of group Y simultaneously by separate servers /teams) is given by T0 . Thus we
should have the ( m![]()
s ) constraints.
ti pi
![]()
T0 , i
![]()
s 1,..., m
(4.3)
For replacement of failed components in the i th subsystem of group X
only ai new components are available. This imposes the constraints:
Consider a system having the group X consisting of 3 subsystems and also the group Y consisting of 3 subsystems. The available time between two missions for repairing and replacing the components is 10 time units. Let the given maintenance cost of the system be 680 units.
0 ![]() pi
pi
![]()
ai andinteger, i
![]()
1,..., s . (4.4)
The other parameters for the various subsystems are given in table
4.1.![]()
If ai ki for some i , i.e. if the number of failed items is less than the
number of available items then the upper bound ai for i th
should be replaced by ki in (4.4).
Finally for group Y subsystems we should have
subsystem
0 ![]() pi
pi
![]()
ki , and integer i
![]()
s 1,..., m . (4.5)
The mathematical programming formulation of the problem is to maximize (4.1) under the constraints (4.2) to (4.5).
required reliability formulated as to
R * , say , of the system then the problem is
IJSER © 2012 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 3, Issue 5, May-2012 4
ISSN 2229-5518
1 (1
0.8)
![]()
(1 p1 )
1 (1
0.75)
![]()
(2 p2 )
1 (1
0.8)
(2 ![]() p3 )
p3 )
1 (1
0.8)
![]()
![]()
(1 p4 )
Max Z
1 (1
![]()
![]()
![]()
![]()
![]()
![]()
0.8)(1 p1 )
1 (1
![]()
![]()
![]()
0.75)(2 p2 )
1 (1
![]()
![]()
0.8)(2 p3 )
1 (1
0.75)(2 p5 )
1 (1
![]()
0.8)(1 p6 )
0.96
1 (1
Subject to![]()
![]()
![]()
0.8)(1 p4 )
1 (1
![]()
0.75)(2 p5 )
1 (1
![]()
0.8)(1 p6 )
120p1
![]()
![]()
105p2
120p3
![]()
50 p4
![]()
40 p5
![]()
50 p6
![]()
850
![]()
4 p4 10
![]()
5 p5 10
![]()
0 p1
0 ![]() p4
p4
![]()
![]()
2 , 0 p2
![]()
3 , 0 ![]() p5
p5
![]()
![]()
2 , 0 p3
![]()
2 , 0 ![]() p6
p6
![]()
1 , and integers.
![]()
3 and integers.
120p1
3 p6
![]()
105p2
![]()
10
![]()
120p3
![]()
50 p4
![]()
40 p5
![]()
50 p6
![]()
680
The above nonlinear programming problem is solved by using LINGO computer program. The optimal Solution obtained after 367 iterations is obtained as
0 ![]() p1
p1
![]()
2 , 0 ![]() p2
p2
![]()
2 , 0 ![]() p3
p3
![]()
1 , and integer
![]()
p1 2, p2
![]()
2, p3
![]()
1 p4
![]()
2, p5
![]()
![]()
2, p6 2
0 ![]() p4
p4
![]()
3 , 0 ![]() p5
p5
![]()
2 , 0 ![]() p6
p6
![]()
3 and integer.
![]()
with minimum maintenance time 24 .
Note that the upper bound for
P2 is kept as 2 because only two
components got failed in subsystem 2 although the available new components are 3.
The above nonlinear programming problem is solved by using LINGO computer program. The optimal Solution obtained after 264 iterations is as follows:
[1] Cassady, C.R., Pohl, E.A., Murdock, W .P., (2001); Selective Maintenance Modeling for Industrial Systems; Journal of Quality in Maintenance Engineering, 7(2), 104-117.
[2] Cassady, C.R., Murdock, W .P., Pohl, E.A., (2001); Selective Maintenance for Support Equipment Involving Multiple Maintenance Actions; European Journal of Operational Research; 129(2): 252-![]()
p1 2, p2
![]()
1, p3
![]()
0 p4
![]()
2, p5
![]()
2, p6
![]()
3 with MaxZ
![]()
0.9248
[3] Cheng C, Meng M, Zuo MJ., (1999); Selective maintenance
So in subsystems 1, 2, and 3 we replace 2, 1, and 0 component
respectively while in the subsystems 4, 5 and 6 we repair and then
replace 2, 2 and 3 components respectively.
optimization for multi-state system. Proceedings of IEEE Canadian
Conference on Electrical and Computer Engineering.
[4 ] Chern, M. S., (1992); On the computational complexity of reliability redundancy allocation in a series system. Operations Research Letters, 11:309–315.
[5] Henley, E. J., & Kumampto, H., (1985); Design for reliability and safety control. New Jersey: Prentice-Hall.
[6] Lust T, Roux O, Riane F., (2009); Exact and heuristic methods for
MinZ
![]()
120p1
![]()
105p2
![]()
120p3
![]()
50 p4
![]()
40 p5
![]()
50 p6
the selective maintenance problem. European Journal of
Subject to
Operational Research; 197:1166–1177.
[7] Rice, W .F., Cassady, C.R., and Nachlas, J.A., (1998); Optimal
1 (1
![]()
![]()
0.8)(1 p1 )
1 (1
![]()
0.75)(2 p2 )
1 (1
![]()
0.8)(2 p3 )
1 (1
![]()
![]()
![]()
0.8)(1 p4 )
Maintenance Plans under Limited Maintenance Time, Industrial
Engineering Research 98 Conference proceedings.
[8] Painton, L., & Campbell, J. (1995). Genetic algorithms in
1 (1
0.75)(2 p5 )
1 (1
0.8)(1 p6 )
0.96
optimization of system reliability. IEEE Transactions on Reliability,
4 p4
5 p5
3 p6
![]()
0 ![]() p1
p1
![]()
10
![]()
10
![]()
10
2 , 0 ![]() p2
p2
![]()
2 , 0 ![]() p3
p3
![]()
1 , and integer
[9] W ang, Z.H., (1992); Reliability engineering theory and practice (5th ed.).Taipei: Quality Control Society of Republic of China.
![]() Dr.Mohammed Faisal Khan received Ph.D from Lucknow integral University and M. Sc from Jamia Millia Islamia New Delhi, India.
Dr.Mohammed Faisal Khan received Ph.D from Lucknow integral University and M. Sc from Jamia Millia Islamia New Delhi, India.
![]()
E-mail: faisalkhan004@yahoo.com
![]()
0 p4
![]()
![]()
3 , 0 p5
![]()
![]()
2 , 0 p6
![]()
3 and integer.
Aligarh Muslim University, Aligarh, India. Presently he is pursuing Ph.D. from department of Statistics and Operations
The above nonlinear programming problem is solved by using LINGO
computer program. The optimal Solution obtained after 505 iterations is as follows:
research Aligarh Muslim University, Aligarh, India.![]()
p1 2, p2
![]()
2, p3
![]()
1 and p4
![]()
2, p5
![]()
![]()
2, p6 2
![]()
with minimum maintenance cost 850 .
MinZ
![]()
4 p4
![]()
5 p5
![]()
3 p6
Subject to
IJSER © 2012 http://www.ijser.org