International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 388

ISSN 2229-5518

Advanced Fibonacci sequence with Golden Ratio

Megha Garg1*, Pertik Garg1, Dr. Ravinder kumar Vohra2

1*, Research Scholar,PTU, jalandhar garg3032@gmail.com

1Research Scholar PTU, jalandhar, way2garg@gmail.com

2Professor, BGIET, Sangrur r.k.vohra49@gmail.com

Abstract— In this paper identity in advanced Fibonacci Series by using the coefficient of this Series described. The

Fibonacci Series is made from Fn+2 = F n + F n+1 . A new Sequence is made by using the two digits 1, 2 which is Fn+2 =
1.Fn +2. Fn+1 . This formula represents a new sequence which is parallel to the Fibonacci sequence. The name given to this series is advanced Fibonacci sequence. The identity F2n+2 – F2 n = 22 Fn+1 (Fn+1 + Fn), has been proved by this series
and the golden ratio of this sequence is √2 + 1.

Key words: Identity, ratio in advanced Fibonacci Sequence, Golden Ratio, Fibonacci Sequence.

1 INTRODUCTION

1. INTRODUCTION

——————————  ——————————

integers are? Yes! The Fibonacci numbers again!)

The Fibonacci numbers were first discovered by a man named Leonardo Pisano. He was known by his nickname, Fibonacci. The Fibonacci sequence is a sequence in which each term is the sum of the 2 numbers preceding it. The first 10 Fibonacci numbers are: (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, and 89). These numbers are obviously recursive.
Fibonacci was born around 1170 in Italy, and he died around 1240 in Italy. He played an important role in reviving ancient mathematics and made significant contributions of his own. The Fibonacci sequence is also used in the Pascal triangle. The sum of each diagonal row is a Fibonacci number. They are also in the right sequence: 1,
1,2,5,8.........
Fibonacci sequence has been a big factor in many patterns of things in nature.
We can make another picture showing the Fibonacci numbers 1,1,2,3,5,8,13,21,
If we take the ratio of two successive numbers in Fibonacci series, (1 1 2 3 5 8 1 3...) we find:

1/1=1; 2/1=2; 3/2=1.5; 5/3=1.666...; 8/5=1.6; 13/8=1.625

Greeks called the golden ratio and has the value 1.61803.

It has some interesting properties, for instance, to square it, you just add 1. To take its reciprocal, you just subtract 1. This means all its powers are just whole multiples of itself plus another whole integer (and guess what these whole

Fibonacci numbers are a big factor in Math.

1.1 Fibonacci is credited for two things:

1.1.1 Introducing the Hindu-Arabic place-valued decimal system and the use of Arabic numerals into Europe. (Can you imagine us trying to multiply numbers using Roman numerals?)

1.1.2 Developing a sequence of numbers (later called the Fibonacci sequence) in which the first two numbers are one, then they are added to get 2, 2 is added to the prior number of 1 to get 3, 3 is added to the prior number of 2 to get 5, 5 is added to the prior number of 3 to get 8, etc. Hence, the sequence begins as

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc Allows users to distribute parallelized workloads to a shared pool of resources to automatically find and use the best available resource. The ability to have pieces of work run in parallel on different nodes in the grid allows the over all job to complete much more quickly than if all the pieces were run in sequence.

1.2 List of Fibonacci numbers

The first 21 Fibonacci numbers Fn for n = 0, 1, 2...20 are:

International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 389

ISSN 2229-5518

The sequence can also be extended to negative index n

using the re-arranged recurrence relation

Fn-2 = Fn - Fn-1 . (1)

which yields the sequence of “negafibonacci” numbers satisfying

F-n = (-1) n+1Fn . (2)

Thus the bidirectional sequence is

Occurrences in mathematics

The Fibonacci numbers are the sums of the "shallow" diagonals (shown in red) of Pascal's triangle

The Fibonacci numbers occur in the sums of "shallow" diagonals in Pascal's triangle (see Binomial coefficient).

head of a sunflower and the seeds are packed in a certain way so that they follow the pattern of the Fibonacci Sequence. This spiral prevents the seed of the sunflower from crowding themselves out, thus helping them with survival. The petals of flowers and other plants may also be related to the Fibonacci sequence in the way that they create new petals.

1.3.1 Petals on flowers

Probably most of us have never taken the time to examine very carefully the number or arrangement of petals on a flower. If we were to do so, we would find that the number

of petals on a flower that still has all of its petals intact and has not lost any, for many flowers is a Fibonacci number:

• 3 petals: lily, iris
• 5 petals: buttercup, wild rose, larkspur, columbine
(aquilegia)
• 8 petals: delphiniums
• 13 petals: ragwort, corn marigold, cineraria,
• 21 petals: aster, black-eyed susan, chicory
• 34 petals: plantain, pyrethrum
• 55, 89 petals: michaelmas daisies, the asteraceae family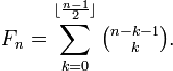

(3)

1.3 Fibonacci sequence in nature.

The Fibonacci Sequence is a pattern of numbers starting with 0 and 1 and adding each number in sequence to the next...0+1=1, 1+1=2 so the first few numbers are
0,1,1,2,3,5,8...and so on and so on infinitely.
One of the most common experiments dealing with the Fibonacci sequence is his experiment with rabbits. Fibonacci put one male and one female rabbit in a field. Fibonacci supposed that the rabbits lived infinitely and every month a new pair of one male and one female was produced. Fibonacci asked how many would be formed in a year. Following the Fibonacci sequence perfectly the rabbits reproduction was determined...144 rabbits. Though unrealistic, the rabbit sequence allows people to attach a highly evolved series of complex numbers to an everyday, logical, comprehendible thought.
Fibonacci can be found in nature not only in the famous rabbit experiment, but also in beautiful flowers. On the

1.3.2 Fibonacci numbers in vegetables and fruit

Romanesque Brocolli/Cauliflower (or Romanesco) looks and tastes like a cross between brocolli and cauliflower. Each floret is peaked and is an identical but smaller version of the whole thing and this makes the spirals easy to see.

Brocolli/Cauliflower

1.3.3 Human Hand

Every human has two hands, each one of these has five fingers, each finger has three parts which are separated by two knuckles. All of these numbers fit into the sequence. However keep in mind, this could simply be coincidence.

International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 390

ISSN 2229-5518

2. Advancement of Fibonacci sequence

The Fibonacci series is a sequence of numbers first created by Leonardo Fibonacci in 1202. The first two numbers of the series is 1 and 1 and each subsequent number is sum of the previous two. Fibonacci numbers are used in computer algorithms. The Fibonacci sequence first appears in the book Liber Abaci by Leonardo of Pisa known as Fibonacci. Fibonacci considers the growth of an idealized rabbit population, assuming that a newly born pair of rabbits, one male, one female and do the study on it. The Fibonacci series become 1, 1, 2, 3, 5, 8, 13, 21 … Now we use the formula by using the next two coefficients of Fibonacci series ie 2 for Fn+1 and 1 for Fn . So the Series become from this formula Fn+2 = 1.Fn +2. Fn+1 is F1 = 1, F2 = 1, F3 =3,7,17,41,99,239,577,1393…… The identity is made from this series is F2n+2 – F2 n = 22
Fn+1 (Fn+1 + Fn) and prove of the series is given below:
We are given that Fn+2 = 1.Fn +2. Fn+1 ……….. (1)
L.H.S. F2 n+2 – F2 n
= ( Fn+2 – Fn ) ( Fn+2 + Fn ) { . . . a2 – b2 = (a-b)(a+b)}
= 2 Fn+1 (Fn+2 + Fn ) { from (1) Fn+2 – Fn = 2 Fn+1 }
= 2 Fn+1 (1.Fn +2. Fn+1 + Fn ) { from (1) the value of Fn+2 is
1.Fn +2. Fn+1 }
= 2 Fn+1 (2. Fn +2. Fn+1 )
Take 2 common from the bracket and we get
= 2.2 Fn+1 ( Fn +Fn+1 )
= 22 Fn+1 (Fn+1 + Fn)
R.H.S
For example: if we take the value of n=1
F2 3 – F2 1 = 22 F2 (F2 + F1) ……………… (2) From the new series the value of
F1 = 1, F2 = 1, F3 = 3
Substitute these values in (2) and we get
(3)2 - (1)2 = 22 . 1 (1 + 1)
9 – 1 = 4 . (2)
8 = 8
Which is true.
Therefore the example satisfies the new sequence which has been made by using the coefficients of Fibonacci Series.

2.1 Golden Ratio:

If we take the ratio of two successive numbers in Fibonacci series, (1 1 2 3 5 8 1 3...) we find:

1/1=1; 2/1=2; 3/2=1.5; 5/3=1.666...; 8/5=1.6; 13/8=1.625

Greeks called it the golden ratio and has the value

1.61803.

The new sequence is 1, 1, 3,7, 17, 41, 99, 239, 577, 1393,
3363 ...we find:
1/1 = 1; 3/1 = 3; 7/3 = 2.3; 17/7= 2.4; 41/17 = 2.41; 99/41

International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 391

ISSN 2229-5518

= 2.414; 239/99 = 2.414, 577/239 = 2.414; 3363/1393
=2.414............
The ratio of this sequence is 2.414. The interesting factor in this ratio is it becomes the value of √ 2 + 1.

References

1. Huylebrouck, Dirk; Gyllenberg, Mats; Sigmund, Karl. "The Fibonacci Chimney". The Mathematical Intelligencer 2000

2. http://www.mathsisfun.com/numbers/fibonacci- sequence.html

3. http://www.maths.surrey.ac.uk/hosted- sites/R.Knott/Fibonacci/fib.html

4. http://www.maths.surrey.ac.uk/hosted- sites/R.Knott/Fibonacci/fibmaths.html

5. The Engineer, "Eden Project gets into flower power".

6. Di Carlo, Christopher (2001). "Interview with

Maynard James Keenan".

7. Ingmar Lehman: Fibonacci-numbers in visual arts and

literature