International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1983

ISSN 2229-5518

ALGORITHM DEVELOPMENT FOR FINGERPRINT IMAGE ENHANCEMENT USING WAVELET PROCESSING

Nwabunwanne Solumtochukwu Ogechukwu N. Iloanusi Charles C. Osuagwu

Department of Electronic Engineering

University of Nigeria Nsukka

somtee8@yahoo.co.uk , ogechukwu.iloanusi@unn.edu.ng

Abstract— This paper presents a technique for fingerprint image enhancement us ing wavelet processing. The algorithm developed uses Daubechies’ wavelets for decomposition as well as reconstruction of the fingerprint image. Experimental results indicate that this algorithm is quite effective, and performs quite competitively with existing methods.

Index Terms — Daubechies’ wavelets, Image enhancement, Fingerprint, Wavelet processing

——————————  ——————————
identities is paramount. The search for such systems culminated recently in biometrics.

1 INTRODUCTION

IN present time, technology has altered to a great

extent the efforts of man to deal with his environment in order to subdue it to meet his needs; with particular reference to electronics. Virtually, all aspects of our modern civilization depend on electronic [including hardware and software] systems for smooth and effective operations of daily activities. Ranging from military, communications, government, education, banking, automobiles and manufacturing to the space industry; all rely on electronic systems for various applications like process automation, control and monitoring systems, security and automated parking control.
Fingerprint based biometric systems have a guaranteed
future as security has become a global challenge with its inherent need for reliable human identification and verification.
Governments, business owners, the organized private sector and educational institutions all require a robust, rugged and dependable means of recognizing and verification of peoples’ identities at various points of access to specific areas physically and electronically.
In order to ensure that intruders, impersonators are promptly fished out prior to breaching the security of these valued resources, information, assets and vaults, a robust and effective means of identifying and verifying peoples’
In the late nineteenth century, it was discovered that no two human beings share the same fingerprint even Siamese twins! This was a revolutionary breakthrough in the world of law enforcement as investigators now had a valid and reliable means of hunting down as well as precisely identify criminals [1].
Biometrics is an emerging technology that is used to
identify people by their physical and/or behavioural characteristics and practically requires the person to be identified to be physically present at the point of identification [2].
Biometric identification relies on those characteristic
features of humans that are inherently unique to individuals such as fingerprints, palmprints, retina, iris, hand geometry, facial features, and ears. Another category of biometrics utilize behavioural characteristics like speech [or voiceprint], lip movement, keystroke dynamics, gait, gesture, signature [2] and thermal emissions etc.
A physiological or behavioural characteristic that is
unique to an individual is referred to as biometric measurement [e.g. voiceprints and fingerprints] which has the capability to reliably distinguish between an authorized person and an imposter [3].
Biometric systems capture these features as digital data using various devices like digital camera, scanners, store them on a database where they serve as templates, retrieve the templates as quickly as possible when required
for verification or authentication at various points of access.

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1984

ISSN 2229-5518

For a fingerprint based biometric system, a typical verification phase involves two stages: enrolment and verification.
Enrolment: this stage capture’s the user’s fingerprint;
its distinctive features [minutiae] are extracted and stored as a template.
Verification: during the verification stage, a new
fingerprint is acquired and compared to the stored template
to verify the user’s claimed identity [4].

2 SUMMARY OF WAVELET TRANSFORM

From the overview of wavelet transform of [5] a summary or wavelet transform is given as:
 Wavelet transform (WT) is a transformation that translates a signal to a multiresolution representation.
 Wavelets relate better to the human sense than other types of transformations e.g. Fourier transform.
 WT features make it indispensable in signal and
must be digitized. Scale and translation factors are chosen based on power of two in practice to avoid over down
sampling (a 2 ; b k2 ). With this, we can write the
equivalent DWT equation as[5]:

W[j k] 2 ∑ f[n]Ψ[2 n k] j k
∈ Z (4)
We can find a set of basis functions using the mother
wavelet Ψ[k], which forms an orthonormal basis and gives a multiresolution analysis framework. Therefore, the

subspace of L (R) covered by these functions is given by:
W Span [Ψ (t)|j k ϵ Z] (5)
Where [Ψ ] = the orthonormal base of W
For multiresolution analysis; a sequence of consecutive
approximation space V (where j = ...-1, 0, 1...) meets the
condition:

… ⊂ V ⊂ V ⊂ V ⋯ (6)
With ∪ ∈ V L (R) (7)
Where L2(R) denotes the vector space of measurable

IJSER

image processing particularly in image
compression and denoising applications.
 Some elegant techniques based on wavelet are capable of yielding effective outcomes than most traditional approaches.
 A wavelet can be seen as a timescale technique integrated with the property of frequency.
Mathematically, a continuous one dimensional wavelet transform (CWT) is the decomposition of a signal f(t) into a
collection of basis functions Ψ (t) known as wavelets.

( ) ∫ ( )Ψ ( ) ( )

Where W(a b) is the wavelet transform WT[ ( )]of f(t).
Given a function Ψ(x), to find its mother wavelet, the
admissibility condition must be satisfied:
|Ψ(s)|

C ∫ ds < ∞ (2)
s
Where Ψ(s) Fourier transform of ψ(x)
Therefore, any ψ(x) that meets this ‘admissibility’ condition
of equation (2) may act as a mother wavelet. While the
wavelets produced from a mother wavelet through dilation
and translation are:
square-integrable one dimensional functions of f(x).
Z denotes the set of integers within the vector space L2(R). R denotes the set of real numbers within the vector space.
∩ ∈ V {0} (8)
For all j ∈ z, we express W to be the orthogonal
complement of V , hence V is given as:
V V ⊕ W j ∈ Z (9)
V ⊥ W applying this function, we can easily loop the
decomposition of
V V ⊕ W
V ⊕ W ⊕ W
( 0)
To any level we desire.
Where V = the low frequency of signal referred to as approximation space.
W = the high frequency signal known as detail space (detail space is the multiresolution analysis).

Ψ Ψ (
√a

t b
a ) (3)

3 FINGERPRINT ENHANCEMENT

ALGORITHM BASED ON

referred to as coefficients or basis functions or daughter wavelets.
Where a = the scale factor; b = the translation factor.
For discrete data (signal), we apply discrete wavelet
transform (DWT). Hence, both scale and translation factors

WAVELETS

The block diagram of the proposed algorithm is shown below; it displays the interaction of the various phases in the algorithm.

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1985

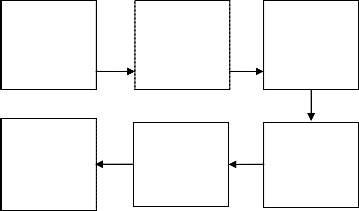
ISSN 2229-5518

INPUT FINGERPRINT IMAGE

DISPLAY ENHANCED FINGERPRINT

IMAGE

NORMALIZE FINGERPRINT IMAGE

WAVELET FILTERING

DECOMPOSI TION USING WAVELETS

RECONSTRU CTION OF ENHANCED FINGERPRINT IMAGE

disappearance of the orientation characteristics of the ridge structure due to over down sampling which occurs at too low a resolution level [7] [8].
The wavelet transform is applied to the normalized image
so as to decompose it into a multiresolution representation. Daubechies wavelet was adopted because it provides sufficient information in the sub-images approximation [7] [8]. The choice of the one level decomposition in addition to the preservation of the ridge pattern to match filtering, also improves computational speed.

Figure 1: Block diagram of fingerprint image enhancement algorithm using wavelet processing

A. Acquisition of fingerprint image

In this phase, the fingerprint image to be enhanced is acquired either directly from a fingerprint scanner or a database such as FVC 2004. Set B database of FVC 2004 was used to experiment the algorithm as it is freely available and contains the required fingerprint images for enhancement.

IJSER

B. Normalization

Here, the primary purpose is to ensure that there is even illumination of the fingerprint image through the generation of specific mean and variance values by adjusting the gray-level values of the input fingerprint image [6]. This phase modifies the gray-level figures between ridges and gorges (furrows or valleys). The process of normalization eliminates the effects of sensor noise as well as gray-level corruption.
Let: F(i, j) represent the gray-level value at pixel location (i, j) of
the input fingerprint image; Mo denotes the estimated mean; Vo represents the estimated variance of input fingerprint image F; FN (i, j) be the normalized output gray-level value at (i, j).
Then the normalized image function is given as [6]:

V

Figure 2: Level 2 Daubechies’ wavelet decomposition; a) level 1 approximation detail, b) level 1 horizontal detail, c) level 1 vertical detail, d) level 1 diagonal detail, e) level 2 approximation detail, f) level 2 horizontal detail, g) level 2 vertical detail and h) level

2 diagonal detail

D. Reconstruction of enhanced fingerprint image

This last phase of the algorithm generates the final enhanced fingerprint image from reconstructing the enhanced approximation image together with the detail sub images of the

F (i j) M + √
V
(F(i j) M ) ( )
decomposition phase. The same wavelet used during the
decomposition process is also applied during reconstruction.
Where M = predefined value of mean; V = predefined variance value
Since normalization is a pixel-wise operation, it does not
affect nor alter the ridge and furrow patterns (or structure); but it cannot modify the visibility of the ridge and valley patterns further.

C. Wavelet Decomposition

The purpose of this phase is to decompose or segment the normalized fingerprint image into approximation image and three sub-details which is a quarter of the original input fingerprint image. It is theoretically supported to decompose an image into sub-images at any level but it is limited to one
decomposition level in this paper. This is to prevent the

E. Wavelet Filtering

This segment of the algorithm smoothes/denoise the fingerprint image using wavelet processing and soft- thresholding techniques. The objective is to optimize the fingerprint image for feature extraction as well as compression for transmission purposes.

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1986

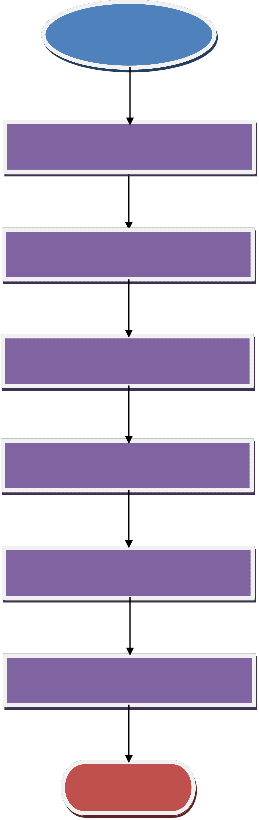
ISSN 2229-5518

Start

Input fingerprint image

Normalize input fingerprint image

Level 2 Daubechies’ wavelet

decomposition

4 EXPERIMENT

The FVC databases are internationally available databases developed for International Competition for Fingerprint Verification Algorithms. FVC is an acronym for fingerprint verification competition. The databases are updated periodically to ensure continuity and available of useful data for researchers in the biometric industry. The purpose of this competition is to set a benchmark that will serve as a reference for practitioners in the industry as well as the academia.
The FVC 2004 [set B] database which is available online at [9] is one of the FVC databases that are generally adopted for evaluating and categorizing fingerprint based biometric system. These databases contain various types of fingerprint images that were captured at varying degrees of quality.
The developed algorithm was tested on images from FVC 2004 set B database. Set B database contains two databases DB-1 and DB- 2 each comprising of 80 fingerprint images out of which 8 images were randomly selected for experimentation.
The images contained in FVC 2004 databases are predominantly
low quality images.
Optical and capacitive sensors that are generally small in size and cheap were applied in generating the fingerprint images of

Reconstruction of enhanced fingerprint image

Wavelet filtering

the FVC databases 1 and 2; while a higher quality optical sensor was deployed for the images of database 3 [10]. The fourth database images were artificially produced by applying the technique presented in [11].
The performance evaluation (PE) formula was adopted to quantify the degree of enhancement achieved by the algorithm. The formula is as given in [12]:
N N N

Output/display enhanced

PE
Total
( 2)

fingerprint image

Stop

Figure 3: Algorithm for fingerprint image enhancement

The flowchart of figure 3 was translated to code using MATLAB
for the implementation of the algorithm.
Where: NM = the number of minutiae that are similar both in algorithm as well as with human expert.
NS = number of super abundant minutiae. NL = number of lost minutiae.
TotalH = the number of minutiae extracted by human expert.
N = total number of fingerprint images used for the experiment. From equation (9), we observe that at NL = NS = 0, and if NM = TotalH; then PE attains its maximum value which is 1.

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1987

ISSN 2229-5518

The algorithm was experimented on 8 fingerprint images which were obtained from DB1- and DB2-set B of FVC 2004 database; the images were generally of size 640 x 480 pixel.
Arithmetic mean (μ) was computed using the formula:

μ ∑ x ( 3)
Where μ = Mean; xi = PE value at i
N = 8
Finally the standard deviation (σ) from the mean was
calculated using the expression:

σ √ ∑ (x μ) ( 4)
Where σ = Standard deviation
xi = PE value at i
μ = Mean
N= 8

5 RESULTS

IJSER

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1988

ISSN 2229-5518

Performance Evaluation (PE)
Serial number
Pre-enhancement parameters Post-enhancement parameters
Nm Nl Ns TotalH PE Nm Nl Ns TotalH PE
1 26 3 0 26 0.8846 29 0 1 29 0.9655
2 36 2 0 36 0.944 38 0 2 38 0.9474
3 44 0 2 44 0.9545 37 7 0 37 0.8108
4 39 14 0 39 0.6410 53 0 3 53 0.9434
7 21

I6 J0 21 S0.7143 E27 0R1 27 0.9630

5 26 2 0 26 0.9231 28 0 1 28 0.9643
6 29 0 3 29 0.8966 26 3 2 26 0.8077
8 25 5 0 25 0.8000 30 0 2 30 0.9333
Mean 0.8448 0.9169
Standard
deviation
0.1077 0.0566

Table 1: Performance evaluation (quantification of the degree of enhancement) of the developed algorithm

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1989

ISSN 2229-5518

Table

2 [13]: Comp arison of this algorit hm with other works.

IJSER

International Journal of Scientific & Engineering Research, Volume 5, Issue 1, January-2014 1990

ISSN 2229-5518

From the results of tables 1 and 2 it is evident that an efficient fingerprint image enhancement algorithm has been developed.

6 CONCLUSION

An effective and efficient fingerprint image enhancement algorithm that is based on wavelet processing has been developed. The algorithm reads an input fingerprint image of uneven illumination, normalizes the illumination, decomposes it into approximation, horizontal, vertical and diagonal sub details using Daubechies’ wavelets; computes its inverse wavelet transform and finally denoise the enhanced fingerprint image using wavelet techniques. The algorithm provides high performance results as can be seen from tables 1 and 2.

French (Ed), InfoBase Publishing, New York, 2009.

2. [2] S. Ribaric and I. Fratic, “A Biometric Identification System Based on EigenPalm and EigenFinger Features”, IEEE transactions on Pattern Analysis and Machine Intelligence, Vol. 27, № 11, November 2005, p.

1698.

3. [3] L. Ma, Y. Hong, and T. Tan, “Iris Recognition Using Circular Symmetric Filters”, IEEE Proceedings, 16th Int. Conf. on Pattern Recognition, 2002, pp. 414-417.

4. [4] R. Cappelli, A. Lumini, D. Maio and D. Maltoni, “Fingerprint Image

Reconstruction from Standard Templates”, IEEE Transactions on Pattern

Analysis and Machine Intelligence, Vol. 29, № 9, September 2007, p. 1489.

5. [5] W.-P. Zhang, Q.-R. Wang and Y. Y. Tang, “A Wavelet-Based Method for Fingerprint Image Enhancement”, IEEE Proc. of the 1st Int. Conf. on Machine learning and Cybernetics, Beijing, November 2002, pp

1973 -1977.

6. [6] M. Wen, Y. Liang, Q. Pan, and H. Zhang, “A Gabor Filter Based Fingerprint Enhancement Algorithm in Wavelet Domain”, Proc. of ISCIT2005, IEEE, 2005, pp 1421-1424.

7. [7] K. Sihalath, S. Choomchuay, S. Wada and K. Hamamoto, “Fingerprint Image Enhancement with Second Derivative Gaussian Filter and Directional Wavelet Transform”, IEEE 2010 Second Int. Conf. on Computer Engineering and Applications, IEEE, 2010, pp 112-116.

8. [8] A. M. Paul and R. M. Lourde, “A Study on Image Enhancement

Techniques for Fingerprint Identification”, Proc. of the IEEE Int. Conf. on

Video and Signal Based Surveillance (AVSS’06), IEEE, 2006.

IJSER

101_1 101_1 enhanced

101_2 101_2 enhanced

101_3 101_3 enhanced

109_8 109_8 enhanced

REFERENCES

1. [1] C. Evans, “Criminal Investigations: Crime Scene Investigation”, J. L.

9. [9]http://bias.csr.unibo.it/fvc2004/download.asp.

10. [10] W.-P. Zhang, Q.-R. Wang, and Y. Y. Tang, “A Wavelet-Based Method for Fingerprint Image Enhancement”, Proc. of the 1st Int. Conf. on Machine Learning and Cybernetics, Beijing, IEEE, November 2002, pp

1973-1977.

11. [11] R. Cappelli, A. Erol, D. Maio and D. Maltoni, “Synthetic Fingerprint

–Image Generation”, Proc. of 15th Int. Conf. on Pattern Recognition

(ICPR2000), Barcelona, September 2000.

12. [12] C. Hsieh, E. Lai and Y. Wang, “An Effective Algorithm for

Fingerprint Image Enhancement Based on Wavelet Transform”, Elservier,

2003.

13. [13] S. Hatami, R. Hosseini, M. Kamarei and H. Ahmadi, “Wavelet Based Fingerprint Image Enhancement”, IEEE Int. Symp. On Circuits and Systems, vol. № 5 May 2005, pp 4610-4163.