International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013

ISSN 2229-5518

A new failure criterion for GFRP composite

1591

materials subjected to in-phase and out-of-phase biaxial fatigue loading under different stress ratios

M.Elhadary

Abstract— this studying the fatigue behavior represents one of the most important targets for any new material before being used. This is because; fatigue behavior cannot be predicted and the fatigue failure cannot be expected as in the case of static yielding. The experimental fatigue tests were conducted on thin-walled tubular specimens woven-roving glass fiber reinforced polyester (GFRP), with 0o, 45o and 90o phase shift between bending and torsional moments for two fiber orientations, ([±45]2 and [0,90]2), at different negative stress ratios, R = - 1, -0.75, -0.5, -0.25, 0. A new term was introduced to the Tsai-Hahn criterion to govern the fatigue behavior of the tested specimens, considering the interact effect between the local stre sses and taking into account the variations of the values of (R) , the ratio of (A/B), and phase angle (z) . Good agreement between predictions and

experimental results was obtained for both in-phase and out-of-phase loadings. The new fatigue model is verified by applying it to different experimental data provided by other researchers. The obtained results by the new fatigue model are in good agreements with the experimental data of E-glass/epoxy of unidirectional plies.

Index Terms— Fatigue, Glass fiber, Polyester, Combined moments, Fluctuating stresses, Failure criteria, composite materials, Out-of-phase.

1. INTRODUCTION

——————————  ——————————
Choosing the suitable failure criterion represents the

u u u

main target for many researchers working with materials,

 A , T and

are the ultimate tensile, ultimate transverse
and it represents the first step for new materials before being used in the field. Considering composite materials, specifically, makes it more challenging, because of their very special behavior and characteristics. Besides, it must be noted that, the suitability of a certain criterion differs greatly according to the tested material, and its stress state. Based on constant amplitude fatigue, the theories available for predicting fatigue life can be divided into three categories: Fatigue life models, Phenomenological models, and Progressive damage models. Fatigue life models are based on S-N curves or Goodman–type diagrams. They predict number of cycles to failure without taking into account damage accumulation and at which fatigue failure occurs under fixed load conditions, the present work is considered as one of the studies of that category [1].
Hashin and Rotem [2] proposed first fatigue failure criteria and developed a fiber failure mode and a matrix-
tensile and ultimate shear stress respectively. The criteria
was expressed in three S-N curves which were determined experimentally on testing off-axis unidirectional specimens under uniaxial load as the ultimate strengths are function of fatigue stress level, stress ratio and number of cycles. This criteria is valid only for laminates with unidirectional piles which exhibit two failure modes during fatigue.
Reifsnider and Gao [3] proposed a failure criteria which
is similar to Hashin and Rotem, the only difference is that
they considered average stresses σ and σ in matrix and
fibers. Their criterion is based on average stress formulation
of composite materials derived from Mori-Tanaka method (a method to calculate the average stress fields in homogeneities and their surrounding matrix). The failure


functions for the two failure mechanisms are σ =
X , ( ) + ( ) = 1

u   T 

  

where X and X are fatigue failure functions under tensile

failure mode, expressed as  A   A ,   u     u   1,

 T   

loading for fiber and unreinforced matrix materials and S
is the fatigue failure function of the unreinforced matrix
where

 A and T are the stresses along the fibers and

under shear loading. The failure functions depend on the
transverse to the fibers,  is the shear stress and

————————————————

 Mechanical Eng. Dept., Faculty of Eng., Alexandria University, Alexandria, Egypt

stress ratio R, the number of cycles N, the frequency f, and
S-N curves which are determined experimentally.
Philippidis,V.[4] proposed a multiaxial fatigue criteria
similar to Tsai-Wu quadratic failure criteria for static
loading and expressed as F σ σ + F σ − 1 ≤ 0 ; i, j = 1, 2, 6
IJSER © 2013 http://www.i jser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013

ISSN 2229-5518

1592

where F and F are functions of number of cycles N , the
stress ratio R and the frequency of loading ν . The tensor
components F and F are calculated using the S-N curves which were determined assuming X = X and Y = Y , where X , X , Y , Y are static failure stresses of the material.
They have used laminate properties to predict laminate
behavior instead of lamina properties as the S-N curves for the laminate account for various damage types occurring in different types of composite materials. Their criteria predicted acceptable fatigue failure under multiaxial loading but for each laminate stacking sequence new series of experiments should be conducted. The well-known failure criteria are listed for anisotropic materials for plane stress conditions in Ref. [6].
Atcholi K. E. et al. [5] concluded that, using Hill's function could give good results if the fatigue cycle is symmetric (zero mean stress) and therefore, the smaller difference between tensile and compressive strength has to be accounted for. This is true for unidirectional glass fibre reinforced epoxy. For other materials with more complex structures, complicated functions, as Tsai-Wu criterion may be required. The paper is organized as follows: Section 2 discusses the experimental work. Section 3 introduces the test results. Section 4 is applicability of failure criteria. Section 5 gives conclusions.

2. EXPERIMENTAL WORK

Woven-roving E-glass fibers and polyester resin, with trade name of ―siropol 8330‖, were used to produce the used specimens. Table 1 shows the properties of the tested materials [ASTM. D2150-63]. This resin was prepromoted with Cobalt Naphthenate (6% solution), as an accelerator in percentage of 0.2 % by volume, and Methyl Ethyl Ketone (M.E.K.) peroxide as a catalyst in a percentage of 2% by volume, depending on room temperature. The volume fraction (Vf), in the present work, ranges from 55% to 65% was used; because this range has proved its suitability to ensure specimens with good strength, good adhesion between fibers and matrix, and acceptable mechanical properties.

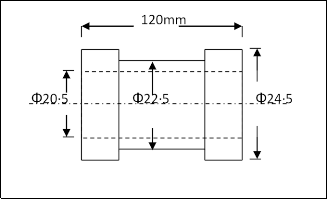
Thin-walled tubular specimens were used for the experimental work to ensure having a plane uniform stress. Fig.1 shows the dimensions of the used specimens. These dimensions are similar to those used by pervious investigators [6,7]. To avoid the failure of some specimens at the end of the gauge length, beneath the grippers, two wooden plugs were inserted into the specimens from both ends. And an elastic sleeve was shrinked on the outer diameter at both ends. A strain controlled testing machine, previously designed by Abouelwafa M.N. et al [8]. It is a constant speed machine of 525 rpm (8.75 Hz); and capable of performing pure torsion, pure bending, or combined torsion and bending (in-phase or out-of-phase) fatigue tests. Fig. 2. shows a general layout for the machine, the loading systems (torsion and bending) are independent, and have the facility to apply different mean stresses.

Fig.1 Dimensions of used specimens

TABLE 1
PROPERTIES OF USED MATERIALS

Fig.2 General layout of the testing machine

IJSER © 2013 http://www.i jser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013

ISSN 2229-5518

3. TEST RESULTS

Specimens were fatigue tested under ambient
TABLE 5

1593

conditions and constant frequency of 8.75 Hz. For each orientation [0,90]2 and [±45]2, the data points were used to plot the corresponding S-N curves on a semi-log scale, being fitted using the power low: Max. Stress = a Nb
Table2 lists the two constants a and b for the corresponding S-N curve for [0,90]2, tested in-phase, with different stress ratios (R = -1, -0.75, -0.5, -0.25, 0) at the ratio of the flexural stress (A) to the torsional shear stress (B), A/B= 2, while Table3 is for [±45]2 at A/B=1. In order to study the effect of mean stress in the presence of a phase difference between the bending and the torsional moments (Z), tests were performed on both fiber orientations, [0,90]2 and [±45]2, at four different stress ratios (R = -1, -0.75, -0.5, -0.25). Table 4 lists the two constants a and b for the corresponding S-N curves for [0,90]2 at all stress ratios with A/B=C/D=2 and Z=45o and 90o, while Table5 is for [±45]2 at A/B=1.
TABLE 2
FATIGUE CONSTANTS (A) AND (B) OF [0,90]2 SPECIMENS WITH
A/B=2 & Z=0O

TABLE 3
FATIGUE CONSTANTS (A) AND (B) OF [±45]2 SPECIMENS WITH
A/B=1 & Z=0O

FATIGUE CONSTANTS (A) AND (B) OF [±45]2 SPECIMENS WITH

A/B=1

4. APPLICABILITY OF FAILURE CRITERIA

All failure criteria have their right hand side to be unity and the left hand side contains the local stress components divided by their corresponding strength. To evaluate the validity of the failure criteria, the right hand side of the failure criteria was considered as a relative damage (R.D). The relation between the relative damage (R.D) with number of cycles to failure (N) is plotted for different failure criteria. In these curves as much as relative damage (R.D) is close to unity, this means that the criterion is suitable. If it is less than unity, then the criterion is predicting a specimen life more than the actual life of the experimental results.
The pervious works for failure criterion used in composite
materials showed that the Tsai-Hahn is the more suitable failure criteria for the tension-compression stress state but it may be modified to make the R.D. of this theory near, as possible as we can, to unity.

 1 1 σ

  1  1 σ

   1

F F

  2

F F

 1t

σ 2

1c   2t

σ 2

2c 

 1 

F1t F1c

2

2

F2t F2c

 2H12σ1σ 2

 σ 

 6 

 

TABLE 4

FATIGUE CONSTANTS (A) AND (B) OF [0,90]

SPECIMENS WITH

 F6 

H12  - 0.5

1

F F F F

(1)

2 1t 1c 2t 2c

A/B=2
A new procedure for adapting this criterion was proposed to best fit the tested case. This procedure was based mainly on introducing a new term to increase the correlation between the experimental data and the theoretical
equations.
IJSER © 2013 http://www.i jser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013

ISSN 2229-5518

The Main Principals for Selecting the New Term are:
 It must depend on the local stress and strength components and not the global ones.
 It should reflect the effect of interact between the local
stresses  1 and  6
 It must take into consideration the effect of variation of stress ratio (R), the ratio of q (A/B), and phase angle (z). It must be dimensionless.
The previous principals had led us to suggest introducing

1594

   

H16

 1 6 

F F

the term
Where,

 1 6  .

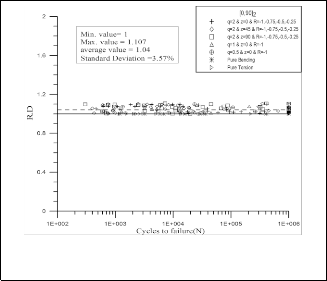
Fig. 4 R.D of the suggested failure criterion for the [0, 90]2

H16 is the normal and shear stresses interaction factor
H16 = (R, Z, q, F1, F6)
The suggested criterion will be as follows:

specimens

 1 1 

  σ

 1 1  2

  σ  1



 1t

F1c 



 2t

F2c 

F1t F1c

2  

 σ 2

 2H σ σ

  σ 6 

F2t F2c

 H16σ1σ 6  1

 

 6 

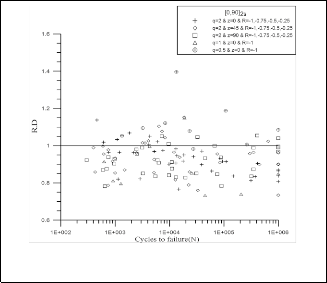
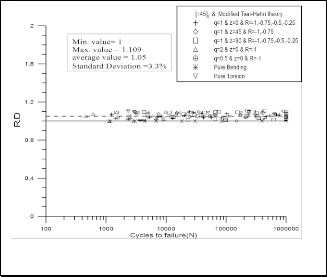
The comparison between the values of R.D. of Tsai-Hahn criterion and the suggested one for both fiber orientations [0, 90]2 and [±45]2 specimens are plotted against the number of cycles to failure as shown in Fig.3 to Fig.6. These figures show that the suggested term has shown excellent results modifying Tsai-Hahn criterion, Equation (1), where, the values of R.D. are around the theoretical value, unity. And the difference may be referred to scatter in experimental

data.

Fig.5 R.D of Tsai-Hahn theory for the [±45]2

specimens

Fig.3 R.D of Tsai-Hahn theory for the [0, 90]2 specimens

Fig.6 R.D of the suggested failure criterion for the [±45]2

specimens

IJSER © 2013 http://www.i jser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013

ISSN 2229-5518

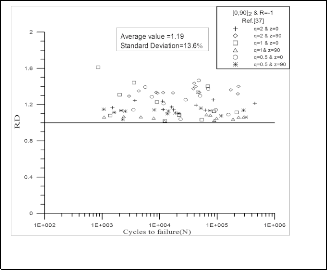
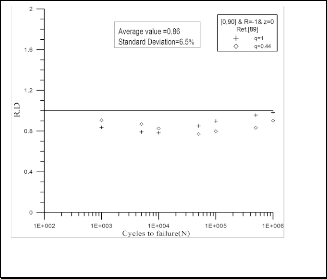
In order to confirm the modified Tsai-Hahn equation, data was obtained from El-Midany A. A. [6] his specimens had nearly the same specifications as those used in this work, being woven-roving GFRP tubular specimens with (Vf) ranging from 50% to 64% and two fiber orientations [0,90]2 and [±45]2. He found that the Tsai-Hahn failure criterion with it’s from as in Equation (1) was the most suitable theory to predict the fatigue life of his experimental data but with relatively high R.D values and high standard deviation as shown in Fig. 7. for the [0, 90]2 specimens with average value of R.D equal to 1.19 and standard deviation of 13.6 %, while, with average value of R.D. equal to 1.18
and standard deviation of 16.1 % for the [±45]2 specimens,

1595

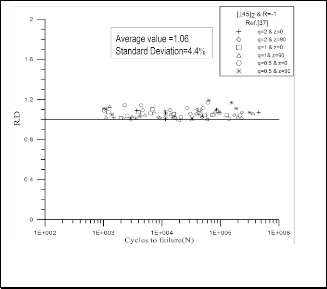
as shown in Fig. 8. Fig,9. and Fig.10. represent the R.D. for the same set of data adapted from El-Midany A. A. [6] but using the suggested failure criterion, for both [0,90]2 and [±45]2 fiber orientations, respectively. These Figures show that an improving in the values of R.D and standard deviation for both fiber orientations when using the modified Tsai-Hahn equation. The average value of R.D for the [0, 90]2 specimens has been improved from 1.19 to 1.03 and standard deviation from 13.6 % to 2.7% and the average value of R.D for the [±45]2 specimens has been improved from 1.18 to 1.06 and standard deviation from
16.1 % to 4.4%.

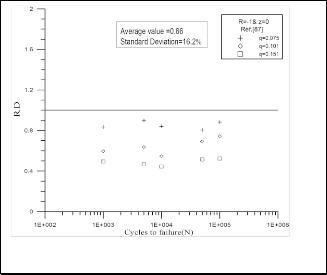
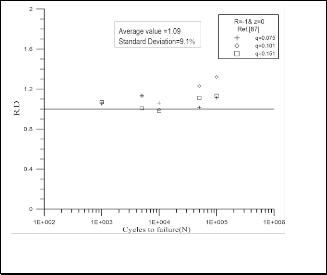
In order to check the validity of suggested failure criterion, presented in this work, for using in a wide range of different materials under different types of loading conditions, data was obtained from Atcholi KE. et al. [5]. They used a unidirectional glass/epoxy composite material with fiber volume fraction (Vf) of 64%. They tested their specimens under completely reversed combined bending and torsional stresses in-phase with zero off-axis angles. The local stresses for these specimens are (1   x , 2  0, 6   xy ) . Fig.11 represents the R.D using Equation (1), while Fig. 12 represents the R.D using the suggested failure criterion. These Figures show an improving in the values of R.D and standard deviation when using the modified Tsai-Hahn equation. The average value of R.D has been improved from 0.66 to 1.09 and

standard deviation from 16.2 % to 9.1%. Using the same
procedure, Fig.13 and Fig.14 show the change of R.D form
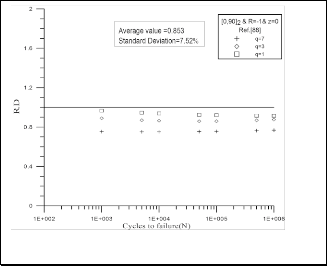
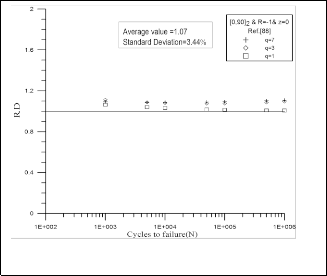
0.853 to 1.07 and standard deviation from 7.52 % to 3.44% using the suggested failure criterion for the data adapted from Kawakami H. et al. [9]. For the data adapted from Amijima S. et al. [10]. Fig. 15 and Fig.16 show the change of R.D form 0.86 to 1.11 and standard deviation from 6.4 % to
5.8% using the suggested failure criterion.

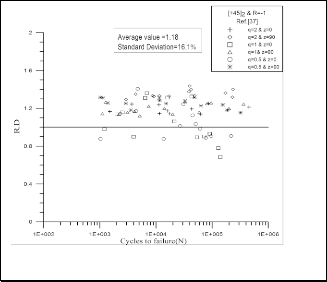
Fig.7 R.D of Tsai-Hahn theory for the [0,90]2 specimens, (Data adapted from El-Midany A. A. [6])

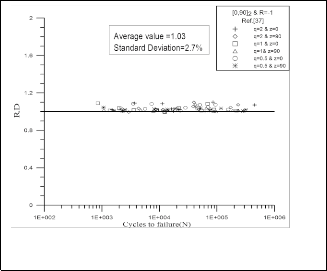
Fig.8 R.D of Tsai-Hahn theory for the [±45]2 specimens, (Data adapted from El-Midany A. A. [6])

Fig.9 R.D of suggested failure criterion for the [0,90]2 specimens, (Data adapted from El-Midany A. A. [6])

IJSER © 2013 http://www.i jser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013

ISSN 2229-5518

1596

Fig.10 R.D of suggested failure criterion for the [±45]2

specimens, (Data adapted from El-Midany A. A. [6])

Fig.13 R.D of Tsai-Hahn criteria for data adapted from Kawakami

H. et al. [9].

Fig.11 R.D of Tsai-Hahn criteria for data adapted from Atcholi

KE. et al. [5].

Fig.14 R.D of suggested failure criterion for data adapted from

Kawakami H. et al. [9].

Fig.12 R.D of suggested failure criterion for data adapted from

Atcholi KE. et al. [5].

Fig.15 R.D of Tsai-Hahn criteria for data adapted from Amijima

S. et al. [10].

IJSER © 2013 http://www.i jser.org

International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013

ISSN 2229-5518

1597

[7] Abouelwafa M.N., Gomaa A., Hamdy A.H., E. Morsi and M.

Nasr" A new failure criterion for fibrous composites subjected to tension-compression local plane stresses", Alexandria Engineering Journal, Vol. 45 , No. 6, pp. 647-656, 2006.

[8] Abouelwafa M. N., Hamdy A. H., and Showaib E. A. "A New

Testing Machine for Fatigue Under Combined Bending and Torsion Acting Out-of phase ", Alexandria Engineering Journal, Vol. 28, No. 4, pp. 113-130, 1989.

[9] Kawakami H, Fujii T, Morita Y. " Fatigue degradation and life prediction of glass fabric polymer composite under tension/torsion biaxial loadings". J Reinf. Plast. Composites, , Vol.

15, pp.183–95, 1996.

[10] Amijima S, Fujii T, Hamaguchi M. "Static and fatigue tests of woven glass fabric composite under biaxial tension–torsion loading". Composites, Vol.22(4), pp. 281–9, 1991.

Fig.16 R.D of suggested failure criterion for data adapted from

Amijima S. et al. [10].

5. CONCLUSION

A new fatigue failure criterion is introduced in this research for GFRP composites. In the new fatigue model all stress components and their interactions are responsible for fatigue failure. The new criterion shows excellent agreement between predictions and experimental data of the fatigue tests conducted on thin-walled tubular specimens woven-roving glass fiber reinforced polyester (GFRP), with 0o, 45o and 90o phase shift between bending and torsional moments for two fiber orientations, ([±45]2 and [0,90]2), at different negative stress ratios, R = - 1, -
0.75, -0.5, -0.25, 0. Also, the new fatigue model is in good agreements with the experimental data reported in the literature of E-glass/epoxy of unidirectional plies.

REFERENCES

[1] Praveenkumar Munagala, "Fatigue Life Prediction of GFRP Composite Material at Coupon and Component Level ", PhD. Thesis, Morgantown, West Virginia,2005.

[2] Hashin Z and Rotem A, "A fatigue criterion for fiber reinforced composite materials", Journal of composite materials 33(7), pp.

448-464, 1973.

[3] Reifsnider KL ang Gao Z, ―A micromechanics model for

composites under fatigue loading, International Journal of fatigue

13(2), 149-156, 1991.

[4] Philippidis TP and Vassilopoulos AP, "Fatigue strength prediction under multiaxial stress", Journal of Composite Materials 33(17), 1578-1599, 1999.

[5] Atcholi K. E., Oytana C., Varchon D., and Perreux D. "Superposed Torsion-Flexure of Composite Materials: Experimental Method & Examples of Applications", J. of Composite Materials, Vol. 23, pp. 327-333, September 1992.

[6] El-Midany A. A. "Fatigue ofWoven-Roving Glass Fibre

Reinforced Polyester Under Combined Bending and Torsion ", PhD. Thesis, Alexandria University-Egypt, 1995.

IJSER © 2013 http://www.i jser.org