International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 234
ISSN 2229-5518
A Survey on 64 Bit Floating Point Multiplier
Based on Vedical Multiplication Techniques
Pranal D. Kale, Prof.M. N. Thakre, Prof. Mrs. R. N. Mandavgane
Abstract— Floating point number’s multiplication is the most important process in the area of graph theory, multidimentional graphics, and digital signal processing, high performance computing etc. However, computers use binary numbers and it would like more precision however, it was found that binary numbers should be precise enough for most scientific and engineering calculations. So it was decided to double the amount of memory allocated. The Binary Floating point numbers are represented in Single and Double formats. The Single consist of 32 bits and the Double consist of 64 bits. The formats are composed of 3 fields; Sign, Exponent and Mantissa. The performance of Mantissa calculation Unit dominates overall performance of the Floating Point Multiplier. Many researchers have investigated the design of multiplier with different approaches. In this paper, we present the overview of work done by various researchers in their literature towards the design of Floating Point Multiplier. The creation of floting point units under a collection of area, latency and throughput constraint is an importantant consideration for system designers.
Index Terms— floting point multiplier, Vedic Mathematics.
—————————— ——————————
Floating-point numbers are widely adopted in many applica- tions due their dynamic representation capabilities. Floating- point representation is able to retain its resolution and accura- cy compared to fixed-point representations. A large number of FP multiplications are carried out in various applications such as scientific calculation and computer graphics (CG). CG, in particular, requires enormous amount of FP multiplications to obtain high quality images required for multimedia systems. It is also of key importance to many modern applications such as
3D graphics accelerators, Digital Signal Processors (DSPs),
High Performance Computing etc.
These applications usually involve floating point calcula-
tions with double precision format. The growing computa-
tional demands of scientific applications shows that in many cases there is a need for increased precision in floating point calculations. Examples are the fields of computational physics, computational geometry, climate modeling etc., which require high precision calculations and great accuracy.
Double precision binary floating-point is a commonly used
format on PCs, due to its wider range over single precision floating point, even if at a performance and bandwidth cost. These applications usually require floating point calculations with double precision format, because this improves the accu- racy of calculations and leads to more reliable results. For this reason, most Floating Point Units (FPUs) tend to provide sup- port for executing double precision operations.
The IEEE 754 standard provides the format for representation of binary floating point numbers [7]. The Binary Floating point numbers are represented in Single and Double formats. The Sin-
————————————————
• Pranal D. Kale is currently pursuing masters degree program in VLSI from
B.D.C.O.E., Sevagram in RTMNU, Nagpur University, India, Mo-9604214478. E-mail: pranalkale @gmail.com
• Prof.Mr. M. N. Thakre sir is currently working as Associate Professor in
B.D.C.O.E.,Sevagram,Mo.9423620513 E-mail: mnt_ent@rediffmail.com
• Prof.Mrs. R. N. Mandavgane is currently working as Professor in
B.D.C.O.E.,Sevagram,Mo. 9823570887 E-mail: rmandavgane@rediffmail.com
gle consist of 32 bits and the Double consist of 64 bits. The Fig1 shows the structure of Single and Fig2 shows the structure Dou- ble formats of IEEE 754 standard. The formats are composed of
3 fields; Sign, Exponent and Mantissa. For single precesion format, the Mantissa is represented in 23 bits and 1bit is added to the MSB for normalization, Exponent is represented in 8 bits which is biased to 127 and MSB of Single is reserved for Sign
bit. For Double precesion format, the Mantissa is represented in 52 bits, the Exponent is represented in 11 bits which is bi- ased to 1023 and the MSB of Double is reserved for sign bit. For both When the sign bit is 1 that means the number is nega- tive and when the sign bit is 0 that means the number is positive
![]()
![]()
The performance of Mantissa calculation Unit dominates overall performance of the Floating Point Multiplier. This unit requires unsigned multiplier for multiplication of BITs.
The Vedic Multiplication technique is one of the technique for the implementation of this unit. The Vedic multiplication sys-
tem is based on 16 Vedic sutras, which describes natural ways of solving a whole range of mathematical problems. Bharati Krishna Tirthaji, who was also the former Shankaracharya (major religious leader) of Puri, India, delved into the ancient
IJSER © 2014 http://www.ijircst.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 235
ISSN 2229-5518
Vedic texts and established the techniques of this system in his pioneering work, Vedic Mathematics (1965), which is consid- ered the starting point for all work on Vedic mathematics. Ac- cording to Mahesh Yogi, The sutras of Vedic Mathematics are the software for the cosmic computer that runs this universe. A great deal of research is also being carried out on how to develop more powerful and easy applications of the Vedic sutras in geometry, calculus and computing. Conventional mathematics is an integral part of engineering education since most engineering system designs are based on various math- ematical approaches. The need for faster processing speed is continuously driving major improvements in processor tech- nologies, as well as the search for new algorithms. The Vedic mathematics approach is totally different as well as fast and considered very close to the way a human mind works.
According to IEEE-754 standards, the floating point number is represented as:
V= (-1) sign * 2exponent-bias*1.fraction [1]
Implicit bit is used before fraction or mantissa, which is „1 for normalized number and, 0 for un-normalized number. Expo- nent bias is (2e-1), which comes out to be 127 for single preci- sion and 1023 for double precision exponent.
Floating point multiplication is not as simple as integer multi-
plication. Designing of a floating point multiplier of floating point numbers represented in IEEE 754 format can be divided in different units:
Mantissa Calculation Unit
Exponent Calculation Unit
Sign Calculation Unit
Control unit
Sign of the result is calculated by XORing sign bits of both the
operands A and B.
Exponents of two multiplying numbers will be added to
get the resultant exponent. Addition of exponent will be using adder.
The Mantissa Calculation Unit requires a multipler. This unit requires unsigned multiplier for multiplication. There are number of techniques that can be used to perform multiplica- tion. Main considering factors are latency, throughput, area, and design complexity. Research work on floating point mul- tiplier is covered by various authers. Review of this research work is given below. In earlier work array multiplication technique was used where two binary numbers A and B, of
‘m’ and ‘n’ bits. There are ‘mn’ summands that are produced
in parallel by a set of ‘mn’ AND gates and booth’s multiplica-
tion techniques was used for multiplication where two signed
binary numbers multiplied in two’s complement notation. The
algorithm was invented by Andrew Donald Booth. As com-
pared to array multiplication booth’s multiplication is faster. In array multiplier for n x n multiplier requires n(n-2) full ad- ders, n half-adders and n2 AND gates. Also, in array multipli-
er worst case delay would be (2n+1) td . Booth’s floating point multiplier is faster than the array multiplier, by calculating the delay value we can get that power dissipation is also less compare to array multiplier. In BOOTH multiplication algo- rithm to reduce the time needed for multiplication number of partial products to be added are reduced. BOOTH recording reduces the number of adder units needed and hence reduced the delay by reducing number of nonzero bits in the multiplier [13]. In BOOTH recoding, the long sequence of 1s is replaced by two no zero bits; for example, If digits j through (down to) k are 1s, then,
2j + 2j+1 + …. + 2k+1 + 2k =2j+1 – 2k
This represents, the sequence of additions can be replaced by
an addition of the multiplicand shifted by j+1 positions and a
subtraction of the multiplicand shifted by k positions [12]. The drawback of BOOTH recording is the high power consump- tion and thus reduced efficiency [8]. The multiplier implemen- tation in floating point multiplication is done by Modified Booth Encoding (MBE) multiplier to reduce the partial prod- ucts by half. The multiplier takes care of overflow and under- flow cases. Rounding is not to give more precision when using the multiplier implemented in a multiply and Accumulate (MAC) unit. By using MBE multiplier we increases the speed of multiplication, reduces the power dissipation and cost of a system. The proposed multiplier will be designed and verified using Modelsim with Verilog HDL. Xilinx is used for synthe- sis. This paper presents an implementation of a floating pointmultiplier that supports the IEEE 754 binary interchange- format; one of the important aspects of the presented design- method is that it can be applicable to all kinds of floating- pointmultipliers. The present design is compared with anor- dinary floating point array multiplier and modified Booth en- coder multiplier via synthesis. It shows that Booth’s floating- point multiplier is faster than the array multiplier, by seeing the delay value we can know this factor and power [9].
Implement multiplier for both conventional, as well as Vedic mathematical methods in VHDL language and highlight a comparative study of both approaches in terms of gate delays. The functional verification through simulation of the VHDL code was carried out using ModelSim SE 6.0 simulator. The synthesis is done using Xilinx Synthesis Tool (XST) available with Xilinx ISE 9.1i. The design is optimized for speed and area using Xilinx, device family Spartan3. In this paper, it is observed that 86.71% lesser slice and also around 88% lesser four input look-up are utilized for Vedic multiplier compared
IJSER © 2014 http://www.ijircst.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 236
ISSN 2229-5518
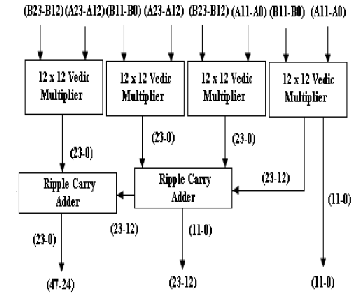
to other multipliers. It shows that 8 bit Vedic multiplier achieves higher speed by reducing gate delay by factor of 24% compared to array multiplier and around 18.2% compared to booth multiplier. Similarly, 16 bit Vedic multiplier achieves higher speed by reducing gate delay by factor of 39.9% com- pared to array multiplier and around 48.36% compared to booth multiplier [1].
Name of the Multiplie r (16 bit) | Number of slices | No of IOs | 4 input LUTs | Bonded IOBs | Delay |
Array multiplier | 290 out of 768 | 65 | 505 out of 1536 | 64 out of 124 | 70.928 ns |
Booth multiplier | 499 out of 768 | 65 | 923 out of 1536 | 65 out of 124 | 60.809 ns |
Vedic multiplier | 120 out of 768 | 90 | 240 out of 1536 | 90 out of 124 | 36.563 ns |
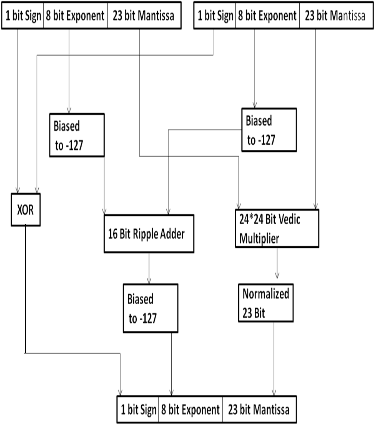
Vedic Multiplication Technique is used to implement IEEE
754 single precision (32 bits) Floating point multiplier. The
Urdhvatri- yakbhyam sutra is used for the multiplication of Mantissa. The underflow and over flow cases are handled. The inputs to the multiplier are provided in IEEE 754, 32 bit for- mat. The multiplier is implemented in VHDL and Virtex-5
FPGA is used. A test bench is used to generate the stimulus
and the multiplier operation is verified. The over flow and under flow flags are incorporated in the design in order to show the overflow and under flow cases The paper shows the efficient use of Vedic multiplication method in order to multi- ply two floating point numbers. The lesser number of LUTs verifies that the hardware requirement is reduced, thereby reducing the power consumption. The power is reduced affec- tively still not compromising delay so much [3].
IJSER © 2014 http://www.ijircst.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014 237
ISSN 2229-5518
Use of numerical methods is prevalent in most software algo- rithms. Computational physics, computational geometry, cli- mate modeling etc., which require high precision calculations and great accuracy. Such applications demand an efficient code for basic mathematical operations i.e. multiplication. Real Time Systems demand instantaneous response to environmen- tal variables and quick execution of taken decision. This moti- vated for an increased precision (64 bits) using ‘time efficient’ method for ‘multiplication’ (Vedic multiplication technique) to improve processor throughput.
Propsed method for designing of a 64 bits double precision
floating point multiplier of floating point numbers represent-
ed in IEEE 754 format is as follows. Initially, two operands will be checked to determine whether they contain a zero. If one of the operands is zero. The output results zero. If neither of them will zero, then the inputs with IEEE754 format will be unpacked and will be assigned to the check sign, add expo- nent and multiply mantissa.
The product is positive when the two operands have the
same sign; otherwise it is negative. Sign of the result is calcu-
lated by XORing sign bits of both the operands A and B
Exponents of two multiplying numbers will be added to get
the resultant exponent. Addition of exponent will be done using 16 bits adder. Exponents will be expressed in excess
1023 bit.
The Mantissa Calculation Unit requires a 53 bit multiple.
This unit requires unsigned multiplier for multiplication of
53*53 BITs. The Vedic Multiplication technique is chosen for the implementation of this unit. This technique gives promis- ing result in terms of speed and power. The Vedic multiplica- tion system is based on 16 Vedic sutras, which describes natu- ral ways of solving a whole range of mathematical problems. Out of these 16 Vedic Sutras the Urdhva triyakbhyam sutra or Nikhilam Sutra will be suitable for this purpose.
From above survey, multiplier is desigined by various tech- niques and observed that Vedic is better than booth’s method and the best than array multiplication method. Floating point multiplications are required in most of the signal processing applications. The growing computational demands of scien- tific applications shows that there is a need for increased pre- cision in floating point calculations like 64 bits and always has scope for improving the speed with the fast multiplication technique by reducing time delay. The Vedic multipliers are much faster than the conventional multipliers. This gives us method for hierarchical multiplier design. So the design com- plexity gets reduced for inputs of large no of bits and modu- larity gets increased. So, propsed work shows Vedic technique can be implemented for double precision floating point multi- plier also for improved efficiency in terms of speed exhibits by
the high speed multiplier algorithm. This will give successful and correct multiplication of two IEEE-754 Standard Double Precision floating point multiplier by using Vedic multipli- cation technique and expected that there is reduction in time delay
The authors like to wish thank’s to all the supportive teaching staff and faculty members, and reference authors who guided by their papers.
[1] S. S. Kerur, Prakash Narchi, Jayashree C N, Harish M Kittur, Gi- rish V A, “Implementation of Vedic Multiplier for Digital Signal Processing,” International Journal of Computer Applications (IJCA) 2011.
[2] Al-Ashrafy, M.; Salem, A.; Anis, “An efficient implementation of floating point multiplier,” Electronics Communications and Pho- tonics Conference (SIECPC), 2011
[3] Aniruddha Kanhe, Shishir Kumar Das, Ankit Kumar Singh, “De- sign and Implementation of Floating Point Multiplier based on Vedic Multiplication Technique” 2012 International Conference on Communication, Information & Computing Technology (ICCICT), Oct. 19-20, Mumbai, Indi.
[4] Kavita Khare, R.P.Singh, Nilay Khare,”Comparison of pipelined IEEE-754 standard floating point multiplier with unpipelined mul- tiplier” Journal of Scientific & Industrial Research Vol.65, pages
900-904 November 2006.
[5] Manish Kumar Jaiswal, Nitin Chandrachoodan “Efficient Imple- mentation of IEEE Double Precision Floating-Point Multiplier on FPGA” 2008 IEEE Region 10 Colloquium and the Third ICIIS, Kha- ragpur, INDIA. December 8-10.
[6] B. Lee and N. Burgess, “Parameterisable Floating-point Operations on FPGA,” Conference Record of the Thirty-Sixth Asilomar Con- ference on Signals, Systems, and Computers, 2002.
[7] Xilinx Floating-Point v2.0. [Online]. Available:
http://www.xilinx.xom
[8] Gokul Govindu, L. Zhuo, S. Choi, V. Prasanna, “ Analysis of High
performance Floating-point Arithmetic on FPGAs”, Proceedings of
18th International Parallel and Distributed Processing Symposium
(IPDPS ’04), pages 149-156, April-2004
[9] P.V.Krishna Mohan Gupta, Ch.S.V.Maruthi Rao, G.R. Padmini,
“An Efficient Implementation of High Speed Modified Booth En- coder for Floating Point Signed & Unsigned Numbers”. Interna- tional Journal of Engineering Research & Technology (IJERT) Vol.
2 Issue 8, August - 2013
[10] P. Saha, A. Banerjee, A. Dandapat, P. Bhattacharyya, “Vedic Mathe matics Based 32-Bit Multiplier Design for High Speed Low Power Proces sors” International Journal On Smart Sensing And Intelli- gent Systems Vol. 4, No. 2, June 2011
[11] G.Vaithiyanathan, K.Venkatesan, S.Sivaramakrishnan, S.Sivaand
S. Jayakumar “Simulation And Implementation Of Vedic Multipli-
er Using Vhdl Code” International Journal of Scientific & Engi- neering Research Volume 4, Issue 1, January-2013 ISSN 2229-5518.
[12] Himanshu Thapliyal, “Modified Montgomery Modular Multipli- cation using 4:2 Compressor and CSA Adder”, Proceedings of the third IEEE international workshop on electronic design, test and applications (DELTA 06), Jan 2005.
IJSER © 2014 http://www.ijircst.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 2, February-2014
ISSN 2229-5518
[13] E.M.Saad, M.Taher, "High speed area efficient FPGA based float ing point arithmetic modules", National conference on radio sci ence (NRSC 2007), March-2007, pp 1-8.
doi:10.1109/ DELTA.2008.19
238
I£ER 2014