International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 488
ISSN 2229-5518
A Parabola Symmetrical to y=x Line
Kundan Kumar
Abstract— This paper presents a parabola symmetrical to the line 𝑦 = 𝑥. A standard parabola is given by the equation 𝑦2 = 4𝑎𝑥 . It is symmetric about x-axis. Another standard equation of the parabola is 𝑥 2 = 4𝑎𝑦. It is symmetric about y-axis. In these equations either 𝑥 or 𝑦 is linear and other one is quadratic in nature. In this paper, I will derive the general equation of a parabola symmetrical to the line 𝑦 = 𝑥 .
Index Terms— Parabola, Symmetry, Types of Parabola, symmetry about 𝒚 = 𝒙 line
—————————— ——————————
There are another forms of parabolas like y = ax2 + bx + c
1 INTRODUCTIO—N———————————————
• KAunRdAanBkOumLaAr iisscuarmrenetmlybAesrsoisftacnotnpircofsesescotrioinnds,epaalrotnmgenwt oitfh ellipse
maantdhemhaytipces rabtoRlai. unPiavrearsbitoyl,aAhims ednaobtada, Infdaiam, PilHy - +o9f19c7u3r7v1e7s6.76T2h. e
Es-tmaanidl:atredchie.qkuntdiaonn@gomf aail.cpoamr,akbuonldaani.sku𝑦m2a=r@4ra𝑎iu𝑥n.ivTerhseityp.eadruabola
𝑦2 = 4𝑎𝑥 is symmetric about x-axis. This is shown in Fig. 1.
Vertex of this parabola is (𝑎, 0) and directrix for this parabola

is 𝑥 + 𝑎 = 0.
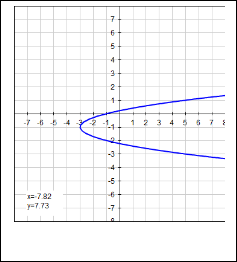
and x = ay2 + by + c. All these are set of parabolas having either quadratic in x or y and linear in other. Hence, the axis of symmetry for the parabolas y = ax2 + bx + c (Fig. 3) and x = ay2 + by + c (Fig. 4) are parallel to y −axis and x −axis respectively. Here, I will discuss about the parabola symmetrical about the line y = x.
Fig. 1 Parabola symmetrical to 𝑥 −axis
Fig. 3 Parabola having axis of symmetry
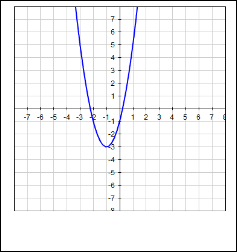
parallel to 𝑦 −axis
Another standard equation of a parabola is x2 = 4ay. The parabola x2 = 4ay is symmetric about y-axis. This is shown in Fig. 2. Vertex of this parabola is (0, a) and directrix for this parabola
is y + a = 0.
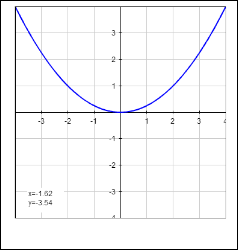
Fig. 4 Parabola having axis of symmetry
parallel to 𝑥 −axis
Fig. 2 Parabola symmetrical to 𝑦 −axis
2 HISTORIES
IJSER © 2015 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 489
ISSN 2229-5518
Menaechmus (380—320 BC) was an ancient Greek mathematician and geometer born in Alopeconnesus in the Thracian Chersonese, who was known for his friendship with the renowned philosopher Plato and for his apparent discovery of conic sections and his solution to the then-long-standing problem of doubling the cube using the parabola and hyperbola. He was trying to duplicate the cube by finding the side of the cube that has an area double the cube. Instead, Menaechmus solved it by finding the intersection of
the two parabolas x2 = y and y2 = 2x.
Euclid (325—265 BC) was a Greek mathematician, often referred
to as the "Father of Geometry". He was active in Alexandria
during the reign of Ptolemy I (323–283 BC). His Elements is one of the most influential works in the history of mathematics, serving as the main textbook for teaching mathematics (especially geometry) from the time of its publication until the late 19th or early 20th century. In the Elements, Euclid deduced the principles of what is now called Euclidean geometry from a small set of axioms. Euclid also wrote works on perspective, conic sections, spherical geometry, number theory and rigor.
Apollonius of Perga (262—190 BC) was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Johannes Kepler, Isaac Newton, and René Descartes. It was Apollonius who gave the ellipse, the parabola, and the hyperbola the names by which we know them. The hypothesis of eccentric orbits, or equivalently, deferent and epicycles, to explain the apparent motion of the planets and the varying speed of the Moon, is also attributed to him.
Pappus (290-350) considered the focus and directrix of the parabola. Pappus gave a description for the parabola that is similar in character to the definition of a circle given earlier. A parabola is fully described by two parameters: a point (its focus) and a line (its directrix). Given the point F and the line d, a parabola C consists of all points that are equally distant from F and d.
Blaise Pascal (1623-1662) was a very influential French mathematician and philosopher who contributed too many areas of mathematics. He worked on conic sections and projective geometry. Pascal considered the parabola as a projection of a
circle.
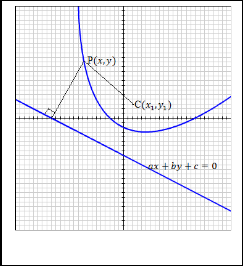
Fig. 5 A general form of the parabola
Symmetry about the line y = x — Any function f(x, y) = 0 is said
to be symmetrical about the line y = x, if there will not be any
change in the equation f(x, y) = 0 after interchanging x and y. so,
due to quadratic and linear nature of x and y in equation y =
ax2 + bx + c and x = ay2 + by + c , the graph of these equations
will not be symmetrical about y = x line.
Since, a Parabola is a geometrical shape. A geometrical shape can
be draw anywhere on coordinate plane regardless of their axis of symmetry. Therefore, it is also possible to sketch a parabola
symmetrical to 𝑦 = 𝑥 line.
4 DERIVATION
Let C(x1 , y1 ) is a fixed point (focus) and ax + by + c = 0 is a
fixed line (directrix).
Let a point P(x, y) is a point on the parabola.
Hence, according to the definition of parabola—
Distance of the point P(x, y) from the focus C(x1 , y1 ) = Length of perpendicular from the point P(x, y) to the line ax + by + c = 0


Therefore, �(x − x1 )2 + (y − y1 )2 =
Galileo (1564-1642) is credited with the discovery of the secrets of
parabolic motion. He did experiments with falling bodies, from
which he deduced the acceleration due to gravity and its independence of the body mass, discovered that projectiles falling
On squaring both sides—
(x − x1 )2 + (y − y1 )2 =
|ax+by+c|
�a2 +b2

(ax + by + c)2
a2 + b2
under uniform gravity follow parabolic paths.
(a2 + b2 )(x2 − 2x1 x + x1 2 + y2 − 2y1 y + y1 2 ) = (ax + by + c)2
2 2 2 2
2 2 2 2 2
Gregory (1638-1675) and Newton (1643-1727) considered the
a2 x2 − 2a2xx1 + a2 x1 + a y
− 2a y1y + a y1 + b x
− 2b x1 x
2 2 2 2 2 2
properties of a parabola which bring parallel rays of light to a
+ b2 x1 + b y
− 2b y1 y + b y1
focus.
= a2x2 + b2 y2 + c 2 + 2abxy + 2bcy + 2cax
2 2 2 2
2 2 2 2 2
−2a2xx1 + a2x1 + a y
− 2a y1y + a y1 + b x
− 2b x1x
3 DEFINITIONS
+ b2 x1 1 12
Definition of a conic section— The locus of point P(x, y), which
= c 2
2 − 2b2y y + b2 y
+ 2abxy + 2bcy + 2cax
2 2 2
2 2 2 2 2
moves so that its distance from a fixed point is always in a
constant ratio to its perpendicular distance from a fixed straight
line, is called a conic section. This constant ratio is called as
b2 x2 + a2 y2 + a2 x1 − 2a xx1 − 2a y1 y + a y1 + b x1 − 2b x1x
− 2b2y1 y + b2 y12
= c 2 + 2abxy + 2bcy + 2cax
2 2 2 2
eccentricity and is denoted by e.
If the eccentricity e is equal to unity, the conic section is called as
b2 x2 + a2y2 + a2 (x1 − 2xx1 − 2y1 y + y1 ) + b (x1 − 2x1 x
− 2y1 y + y1 2 ) = c 2 + 2abxy + 2bcy + 2cax
2 2
parabola.
Definition of Parabola— The locus of point P(x, y), which moves
b2 x2 + a2 y2 + (a2 + b2 )(x1 − 2xx1 − 2y1 y + y1 )
= c 2 + 2abxy + 2bcy + 2cax
so that its distance from a fixed point (called the focus) is always
b2 x2 + a2 y2 + (a2 + b2 )(x1
1 1 1
2 − 2xx
− 2y y + y2 ) − 2abxy +
equal to its perpendicular distance from a fixed straight line (called
2bcy + 2cax + c 2
= 0 (1)
the directrix). (Fig. 5) is called a parabola.
Equation (1) represents a general equation of a parabola.
Now, by substituting a = b and c = 0 in (1),
2 2 2
a2 x2 + a2y2 + 2a2 (x1 − 2xx1 − 2y1 y + y1 ) − 2a xy = 0
IJSER © 2015
http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 6, Issue 2, February-2015 490
ISSN 2229-5518
2 2
x2 + y2 + 2(x1 − 2xx1 − xy − 2y1 y + y1 ) = 0 (2) Equation (2) represents a parabola symmetrical to y = x line.
Again, taking the focus C(x1, y1 ) ≡ C(1,1), “(2)”will
becomes—

x2 + y2 − 2xy − 4x − 4y + 4 = 0 (3) Equation (3) represents a parabola having axis of symmetry y = x line whose vertex is C(1,1) and directrix is y = −x line. (Fig. 6)
Fig. 6 Parabola symmetrical to the line y = x
If focus C(x1 , y1 ) ≡ C(−1, −1), “(2)”will becomes—
x2 + y2 − 2xy + 4x + 4y + 4 = 0 (4)
Equation (4) represents a parabola having axis of symmetry y = x
line whose vertex is C(−1, −1) and directrix is y = −x line. (Fig.

7)
ACKNOWLEDGMENT
The Author thanks Dr. Anjana Bhandari (Previously associate professor in department of mathematics in Rai University, Ahmedabad, India) for their valuable guidance during the work of this paper. Tripathi Abhishek Rajeshwarprasad (Currently pursuing bachelor degree program in computer science and engineering in Rai University, Ahmedabad, India), Shah Krimi Sunilbhai (Currently pursuing bachelor degree program in computer science and engineering in Rai University, Ahmedabad, India) and Patel Khushboo Hasmukhbhai (Currently Pursuing bachelor degree program in electronics and communication engineering in Rai University, Ahmedabad, India) had assisted the author for this paper.
REFERENCES
[1] Sydney Luxton Loney, The Elements of Coordinate Geometry, Cartesian Coordinates PART 1, ISBN: 818822243-7, pp. 161-208
[2] George B. Thomas, Jr., Ross L. Finney, Maurice D. Weir, Calculus and
Analytic Geometry, ISBN: 978-81-7758-325-0, pp. 48-50, pp. 727-762
[3] A Ganesh, G Balasubramanian, The Textbook of Engineering
Mathematics ISBN: 978-81-239-1942-3, pp. 391-415.
[4] http://www.carondelet.pvt.k12.ca.us/Family/Math/03210/page2.htm
[5] http://fcis.aisdhaka.org/personal/chendricks/IB/Tsokos/ Ts2.10ProjectileMo.pdf
[6] http://en.wikipedia.org/wiki/Parabola#cite_note-7
[7] http://www.math.uoc.gr/~pamfilos/eGallery/problems/ ParabolaProperty.html
[8] http://www.math.uoc.gr/~pamfilos/eGallery/problems/
TrianglesCircumscribingParabolas.html
Fig. 7 Parabola symmetrical to the line y = x
5 CONCLUSION
The equation of a parabola may contain the second degree terms in
x and y both. It can be symmetrical about the line y = x.
IJSER © 2015 http://www.ijser.org






