f(t) = bt + c (7) changing the linear equation parameter (b) provides a differ- ent frequency distributions used in the designed LFM , Pa-
rameters used in our simulation is: 20 µ sec pulse width and
|χ(τ, fd |2= ��1 −
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 732
ISSN 2229-5518
A New Biphase Coding LFM for Pulse
Compression Radar
Ahmed Ramadan, Moustafa El-Hoshy, and Alaa El-Din Sayed Hafez
Faculty of Engineering, Alexandria University
E-mail: alaaahafez@yahoo.com
—————————— ——————————
n radar terminology extraction the high resolution spatial profile from received signal is known as pulse compression. The problem matched filter output which makes the detection of weak echo signals accompanied by strong signals from target with high Radar Cross-Section (RCS) difficult or even impossible [1]. A very common pulse compression radar waveform is LFM chirp signal. Its utility is that it is fairly generated by a variety of technologies, and is easily processed by a variety of techniques that ultimately im- plement a matched filter. Large sidelobe level of the ACF causes a serious problem in detection of targets especially in presence of nearby interfering targets or other noise sources. Reducing the sidelobes at the matched filter output is typically accomplished by linear filtering, most often by applying win- dow functions or data tapering. This additional filtering al- lows the matched filter to reduce the sidelobes as desired. However, since the cumulative filtering is no longer precisely matched to the signal, it necessarily reduces output Signal to Noise Ratio (SNR) as well, typically by 1-2 dB (depending on the filtering or weighting function used), also widening the main lobe leads to degradation on radar range resolution. It is well-known that NLFM can advantageously shape the Pow- er Spectral Density (PSD) such that the autocorrelation func- tion exhibits substantially reduced sidelobes[2].Consequently, no additional filtering is required and maximum SNR perfor- mance is preserved. The digital processing or SAW devices can be used to process nonlinear FM. NLFM technique gives
————————————————
• Prof. Dr. Ahmed Ramadan is Electrical Engineering Department Chief,
better SNR performance, because no power is lost by window- ing in the receiver. Different pulse compression techniques have been discussed [3-7], without decreasing the sidelobe level than -23 dB. This paper introduces group of OBPCC. The methodology of obtaining these codes depends on changing the waveform frequency and phase rather than the traditional methods which depends only on the frequency variation. GA has been used to achieve a set of optimized codes [8], but in- creasing the length of the code will often lead to an unac- ceptable slow convergence speed.
The radar ambiguity function represents the output of the matched filter, and it describes the interference caused by the range and/or Doppler shift of a target when compared to a reference target of equal RCS. The ambiguity function evalu-
ated at (τ, fd ) = (0,0) is equal to the matched filter output that
is perfectly matched to the signal reflected from the target of
interest. In other words, returns from the nominal target are
located at the origin of the ambiguity function. Thus, the am-
biguity function at nonzero τ and fd represents returns from
some range and Doppler different from those for the nominal
target [9].
The general formula of the Ambiguity Function (AF) assum-
ing a moving target with Doppler frequency fd can be de-
scribed as follows:
Faculty of Engineering, Alexandria University, Alexandria, Egypt. 2 ∞ 2
• Moustafa El-Hoshy is currently pursuing masters degree program in electronic & Communication engineering in Alexandria University.
Dr. Alaa Hafez, Affiliate Instructor, Faculty of Engineering, Alexandria
�χ(τ, fd � =�∫ x�(t)x� ∗ (t − τ)ej2πfdt dt�
(1)
University, Alexandria , Egypt
The radar ambiguity function is normally used by radar de-
signers as a means of studying different waveforms. It can provide insight about how different radar waveforms may be
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 733
ISSN 2229-5518
suitable for the various radar applications[10]. It is also used to determine the range and Doppler resolutions for a specific radar waveform. The AF of a single pulse can be written as:
f(t) = bt + c (7) changing the linear equation parameter (b) provides a differ- ent frequency distributions used in the designed LFM , Pa-
rameters used in our simulation is: 20 µ sec pulse width and
|χ(τ, fd |2= ��1 −![]()
|τ|�
τo
![]()
sin�πfd(τo−|τ|)� 2
�
πfd(τo−|τ|)
|τ| ≤ τo (2)
chirp bandwidth of (0-50) MHz . The Matched filter output using Fast Fourier Transform (FFT) can be simply described as shown in Fig.1.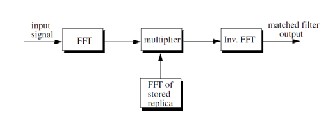
where , τ is the pulse width while τ0 is the compressed pulse
width or effective pulse width. The LFM complex envelope
signal is defined as:![]()
![]()
x�(t) = 1 Rect � t � ejπµt2 (3)
�τo to
The up-chirp ambiguity function cut along the time delay axis
τ is :
Fig.1. Matched filter output using FFT
|τ|
![]()
sin ( πτ (μτ−f )�1−|τ|�) 2
![]()
τo
![]()
|χ(τ, fd |2 = ��1 − �
τo
![]()
πτ (μτ−f )�1−|τ|�
τo
� |τ| ≤ τo
(4)
The sidelobe suppression of the matched filter output using
the designed LFM radar signal has been improved as well, but
far less.
Where, μ is the LFM coefficient and is equal to the bandwidth
(B) divided by the pulse width. It is known that the LFM am-
biguity function cut along the Doppler frequency axis is simi-
lar to that of the single pulse. This is the pulse shape has not
changed (only frequency modulation was added). However, the cut along the time-delay axis changes significantly. It is much narrower compared with the un modulated pulse. On the other side, Stepped Frequency Waveforms (SFW) is a class of radar waveforms that are used in extremely wide band-
The most widely used phase coded waveform employs two phases and is called binary, or biphase, coding. One family of biphase codes that produced compressed waveforms with constant sidelobe level equal to unity is Barker codes. The complex envelope of the phase coded pulse is given by [12],
1 M t − (m − 1)t
width applications where very large time bandwidth product
u(t ) =
![]()
u rect b
T t
(1)
(or compression ratio) is requires [11]. The advent of high- speed Digital-to-Analog Converters (DACs) and high-speed large-scale Field Programmable Gate Arrays (FPGAs) current-
where
m=1
b
ly facilitate generating high-performance precision digital
LFM chirp waveforms. In LFM the transmitter spends equal time at each frequency, hence the nearly uniform spectrum. Another method for shaping the spectrum rather than ampli- tude weighting is to deviate from the constant rate of fre- quency change and to spend more time at frequencies that need to be enhanced. This approach was termed NLFM .
The complex envelope of the NLFM signal is given by :
u(t) = g(t) (5)
where g(t) is the amplitude and ϕ(t) is the phase function. The
um = exp( jφm )
{φ ,φ ,......,φ }
the set of M phases, 1 2 m is the phase code asso-
ciated with u(t) and T is the pulse duration. The biphase codes consist of a sequence of either 0 and 1 or +1 and -1. code ele- ment (l) means amplitude (1) and phase shift (0o) while (-1) means amplitude (1) and phase shift (πo). If a transmitted pulse u(t) with MRuR phase elements defined by um(1≤m≤M) and a reference pulse v(t) with MRvR elements defined by vRnR(1≤n≤MRvR). The cross-correlation function of two phase- coded pulses is defined as [13]:
![]()
Fourier transform can be described as follows:
R (t ) = ∫ u(t )v* (t + t )dt = ∫ ∑u
rect
( ) b .
∞ ∞ 1 M u
uv m
t − m − 1 t
![]()
t
(2)
−∞ −∞
∞
u b m=1
b
U(f) = |U(f)| exp[jϕ(f)] = ∫−∞ g(t) exp�j�−2πft + ϕ(t)�� dt (6)
M v t + t − (n − 1)t
![]()
![]()
∑ vn rect
.dt
In the Design process of the transmitted LFM radar signal ,the matched filter output signal is given by the input filter auto-
M v tb
m=1 tb
correlation function. The signal autocorrelation function is determined by the Inverse Fourier Transform (IFT) of the en- ergy spectral density. Frequency variation of LFM follows a first order equation as follows :
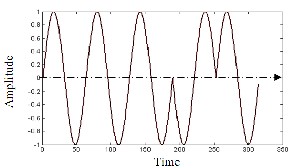
Phase coded signal using five bits [ 1 1 1 -1 1 ] biphase
pulse compression Barker code is shown in Fig.2. where the
phase of the waveform changes according to the code ele-
ments.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 734
ISSN 2229-5518
0
-5
-10
-15
-20
-25
-30
LFM PCLFM
Fig.2. Phase coded signal using Five bits biphase pulse compression code
Genetic algorithm has been used to optimize the pulse compression codes parameters by changing The code value
.Binary encoding scheme is used in this algorithm to encode the code elements [13-15]. The chromosome contains the bi- phase pulse compression code elements, each gene encoded as
-35
-40
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
Fig. 3. PCLFM ACF with 0.002 LFM slope compared with con- ventional LFM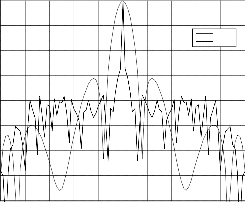
0
-5
1 bit to represent the code element . Elitism is used to save the best solution to improve the performance of genetic algorithm. The algorithm started with a set of solutions called population solutions, one population is used to form a new population, this is motivated by hope that the new population will be bet- ter than the old one .Solutions that are selected to form new off springs are selected according to their fitness .The fitness of pulse compression codes is determined according to two main parameters the PSL and MSL levels. The crossover rate used is randomly selected between 10-90 % , the mutation rate is equal to 3% , the population size is selected to be 64 . The op-
-10
-15
-20
-25
-30
-35
-40
LFM
PCLFM
timization process proceeds to obtain the minimum PSL and
MSL of the biphase pulse compression codes.
Fig.3. show a comparison between ACF of LFM and OBPCC LFM with 0.002 modulation slope which reflects a significant improvement in compression ratio exceeded 9 times that achieved from traditional LFM without any degra-
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
Fig.4. PCLFM ACF with 0.003 LFM slope compared with con- ventional LFM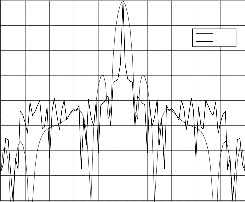
0
-5
LFM PCLFM
dation in SLL. With 0.003 modulation slope significant com-
pression ratio CR achieved with additional SLL reduction by
more than -4 dB over the normal LFM as shown in Fig.4. The same conclusion can be achieved from Figs. (5 to 10) with modulation slopes from 0.004 to 0.009. Fig.11. demonstrate the ambiguity function of LFM signal while OBPCC LFM ambigu- ity function shown in fig.12. Table (1) illustrates the optimized Biphase codes for each modulation slope.
-10
-15
-20
-25
-30
-35
-40
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
Fig.5. PCLFM ACF with 0.004 LFM slope compared with con- ventional LFM
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 735
ISSN 2229-5518
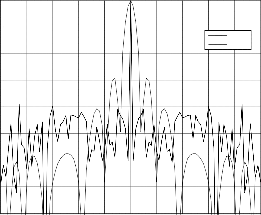
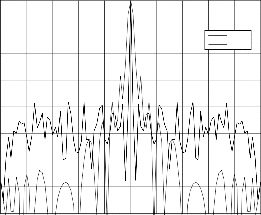
0 0
-5
-10
LFM PCLFM
-5
-10
LFM PCLFM
-15
-15
-20
-20
-25
-25
-30
-30
-35
-35
-40
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
-40
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
Fig.6. PCLFM ACF with 0.005 LFM slope compared with con- ventional LFM
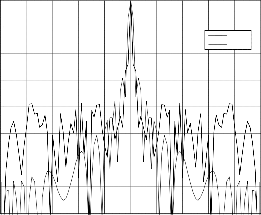
Fig.9. PCLFM ACF with 0.008LFM slope compared with con- ventional LFM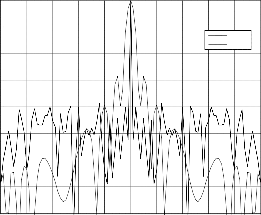
0 0
-5
-10
LFM PCLFM
-5
-10
LFM PCLFM
-15
-15
-20
-20
-25
-25
-30
-30
-35
-35
-40
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
-40
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
Fig.7. PCLFM ACF with 0.006 LFM slope compared with con- ventional LFM
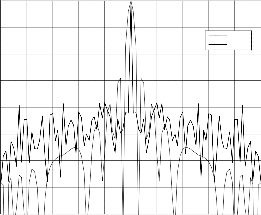
Fig.10. PCLFM ACF with 0.009 LFM slope compared with conventional LFM
LFM

0
-5
-10
LFM PCLFM
1
0.9
-15
0.8
0.7
-20
0.6
0.5
-25
0.4
0.3
-30
0.2
0.1
-35
-40
-50 -40 -30 -20 -10 0 10 20 30 40 50
Time
0
8
6
4
ν*Mt
b
2
0 -50
50
0
t/t
b
Fig.8. PCLFM ACF with 0.007 LFM slope compared with con- ventional LFM
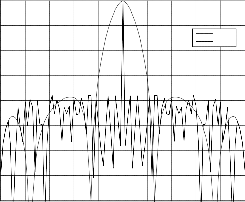
Fig.11. Ambiguity function of the 51-element LFM.
IJSER © 2014 http://www.ijser.org
International Journal of Scientific & Engineering Research, Volume 5, Issue 4, April-2014 736
ISSN 2229-5518
User Defined
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
8
6
ν*Mt
b
4
2
0 -50
0
t/t
b
[1] D.Elizbath Rani, K.SriDevi “Mainlobe Width Reduction Using Linear and
Nonlinear
Frequency Modulation” ,proceeding of the International Conference on
Advances in
Recent Technologies in Communication and Computing,2009. [2] Nadav Levanon, Mozeson , Radar signals, John Wiley, 2004.
[3] Edward I- Titlebaum,Sevtisav v.Maric and Jerome R.Belleg",Ambiguity Properties of Quadratic congruential Coding", IEEE transaction on Aerospace and electronic systems, vol. 27, no.1 January.1991, pp.18-29.
[4]Hon Kaung,Chi Kin Lee " A Neural Netwok Approach to Pulse Radar Detec- tion", IEEE transaction on Aerospace and electronic systems, vol. 29, no.1
January.1993, pp.9-21.
[5]Nadav Levanon" Non coherent pulse compression" ,IEEE transaction on Aero- space and electronic systems, vol.42, no.2 April. 2006,pp.756-765.
50 [6]Shannon D.Blunt and Karl Gerlach "Adaptive pulse compression via MMSE
estimation ",IEEE transaction on Aerospace and electronic systems, vol.42, no.2 April. 2006, pp.572-583.
[7]Stephen R.Gottesman "A Class Of Pseudo noise-Like Pulse Compression
Codes ", IEEE transaction on Aerospace and electronic systems, vol. 28, no.2
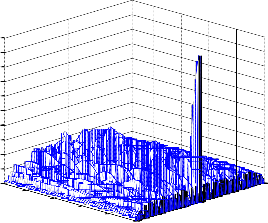
Fig.12. Ambiguity function of the 51-element GA OBPCC LFM., with 0.002 LFM slope
April.1992, pp.355-362.
[8] El-Sayed A. Youssef, Amr Mokhtar, Mohamed Madkour and Mohamed Ab-
del-Latif," A Novel Multilevel Biphase Pulse Compression Codes",ICCTA
2007, 1-3, September 2007, Alexandria, Egypt.
[9] Nadav Levanon and Uri Peer "Non-coherent pulse compression- concept and waveforms," IEEE Israel AP/MTT Symposium, May 15, 2007.
[10] Simon Haykin " Adaptive Radar Signal Processing," John Wiley 2007.
[11] Skolink ,Merrill I,Radar Handbook.3rd ed.New York ; Chicago: McGraw
Hill,2008.
[12] Skolnik, M.I, Radar Handbook, (second addition):New York: McGraw-Hill,
1990.
[13] Bassem R. Mahafza, Radar systems analysis and design using Matlab, New
York: Chapman & Hall/CRC, 2000.
[14]Randy L .Haupt "An introduction to genetic algorithm for electromagnetics ", IEEE, Antennas and propagation magazine, Vol.37, no2, 1995.
[15]Zbigniew Michalewiez, Genetic algorithms + Data strcture = Evolution pro-
grams, Springer, Verlag Berlin Heidelberg, New York ,1996.
This paper proposed Optimized Biphase Pulse Compres- sion Codes (OBPCC) with the LFM waveform. Frequency and phase coding have been used to achieve optimum (SLL) and (CR) using Genetic algorithm (GA). The results compare the ACF for both LFM and phase coded (PCLFM). Set of codes are generated for code length of 51 with frequency modulation index from 0.002 to 0.009. Peak sidelobe level from -18.89 dB to
-19.49 dB is achieved. The results obtained show superiority of PCLFM over the conventional LFM which improves the com- pression ratio by 9.95 times the conventional LFM.
IJSER © 2014 http://www.ijser.org